平面向量的概念及线性运算考点与提醒归纳
- 格式:docx
- 大小:124.65 KB
- 文档页数:14
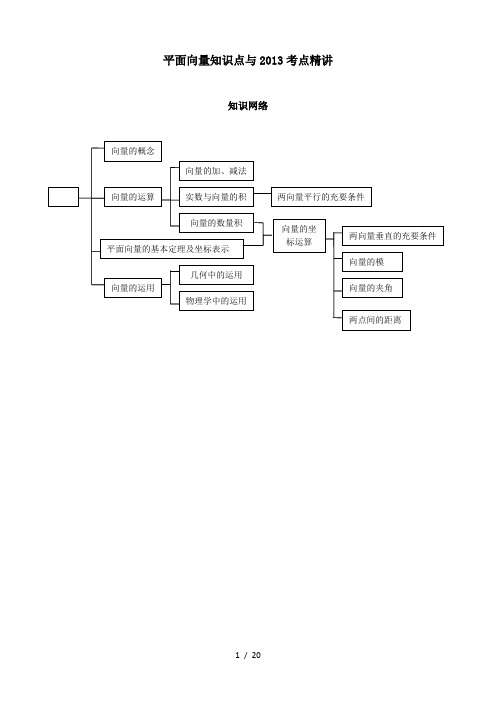
平面向量知识点与2013考点精讲知识网络第1讲 向量的概念与线性运算★ 知 识 梳理 ★1.平面向量的有关概念:(1)向量的定义:既有____大小又有方向_________的量叫做向量.(2)表示方法:用有向线段来表示向量.有向线段的____长度_____表示向量的大小,用_____箭头所指的方向____表示向量的方向.用字母a ,b ,…或用AB ,BC ,…表示.特别提醒:1) 模:向量的长度叫向量的模,记作|a |或|AB |. 2) 零向量:长度为零的向量叫做零向量,记作0;零向量的方向不确定. 3) 单位向量:长度为1个长度单位的向量叫做单位向量.4) 共线向量:方向相同或相反的向量叫共线向量,规定零向量与任何向量共线. 5)相等的向量:长度相等且方向相同的向量叫相等的向量.2.向量的线性运算 1.向量的加法:(1)定义:求两个向量和的运算,叫做向量的加法.如图,已知向量a ,b ,A ,作AB =u u u ra ,BC =u u u rb ,则向量AC 叫做a 与b 的和,记作a+b ,即 a+b AB BC AC =+=u u u r u u u r u u u r特殊情况:abab a+bbaa+b(1)平行四边形法则三角形法则CBDCBabba +ba +AABC C)2()3(对于零向量与任一向量a ,有 a 00+=+ a = a(2)法则:____三角形法则_______,_____平行四边形法则______(3)运算律:____ a +b =b +a ;_______,____(a +b )+c =a +(b +c )._______ 2.向量的减法:(1)定义:求两个向量差的运算,叫做向量的减法. 减法的三角形法则作法:在平面内取一点O , 作OA = a , = b , 则= a - b即a - b 可以表示为从向量b 的终点指向向量a 的终点的向量注意:1)AB表示a-b强调:差向量“箭头”指向被减数2)用“相反向量”定义法作差向量,a-b = a +(-b)显然,此法作图较繁,但最后作图可统一a∥b∥c a - b = a + (-b) a - b3.实数与向量的积:(1)定义:实数λ与向量a的积是一个向量,记作λa,规定:|λa|=|λ||a|.当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向相反;当λ=0时,λa=0.(2)运算律:λ(μa)=(λμ)a,(λ+μ)a=λa+μa,λ(a+b)=λa+λb.特别提醒:1)向量的加、减及其与实数的积的结果仍是向量。



第一节平面向量的概念及其线性运算1.向量的有关概念(1)向量:既有大小,又有方向的量叫向量;向量的大小叫做向量的模.(2)零向量:长度为0的向量,其方向是任意的.(3)单位向量:长度等于1个单位的向量.(4)平行向量:方向相同或相反的非零向量,又叫共线向量,规定:0与任一向量共线.(5)相等向量:长度相等且方向相同的向量.(6)相反向量:长度相等且方向相反的向量.例1.若向量a与b不相等,则a与b一定()A.有不相等的模B.不共线C.不可能都是零向量D.不可能都是单位向量例2..给出下列命题:①若|a|=|b|,则a=b;②若A,B,C,D是不共线的四点,则AB=DC等价于四边形ABCD为平行四边形;③若a=b,b=c,则a=c;④a=b等价于|a|=|b|且a∥b;⑤若a∥b,b∥c,则a∥c.其中正确命题的序号是()A.②③B.①②C.③④D.④⑤CA2.向量的线性运算向量运算定义法则(或几何意义)运算律加法求两个向量和的运算三角形法则平行四边形法则(1)交换律:a+b=b+a;(2)结合律:(a+b)+c=a+(b+c)减法求a与b的相反向量-b的和的运算叫做a与b的差三角形法则a-b=a+(-b)数乘求实数λ与向量a的积的运算(1)|λa|=|λ||a|;(2)当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向相反;λ(μa)=(λμ)a;(λ+μ)a=λa+μa;λ(a+b)=λa+λb例3:化简AC→-BD→+CD→-AB→得() A.AB→B.DA→C.BC→D.0例4:(1)如图,在正六边形ABCDEF中,BA+CD+EF=()A.0B.BE C.AD D.CF(2)设D,E分别是△ABC的边AB,BC上的点,AD=12AB,BE=23BC.若DE=λ1AB+λ2AC(λ1,λ2为实数),则λ1+λ2的值为________.巩固练习:1.将4(3a+2b)-2(b-2a)化简成最简式为______________.2.若|OA→+OB→|=|OA→-OB→|,则非零向量OA→,OB→的关系是() A.平行B.重合C.垂直D.不确定3.若菱形ABCD的边长为2,则|AB-CB+CD|=________4.D是△ABC的边AB上的中点,则向量CD等于()A.-BC+12BA B.-BC-12BA C.BC-12BA D.BC+12BA5.若A,B,C,D是平面内任意四点,给出下列式子:①AB+CD=BC+DA;②AC+BD=BC+AD;③AC-BD=DC+AB.其中正确的有()A.0个B.1个C.2个D.3个6.如图,在△ABC中,D,E为边AB的两个三等分点,CA→=3a,CB→=2b,求CD→,CE→.DD12巩固练习1。

平面向量知识点梳理第一篇:一、平面向量的基本概念及表示方法1. 平面向量的定义:平面向量是具有大小和方向的量,用箭头表示。
2. 平面向量的表示方法:平面向量通常用有向线段来表示,线段的长度表示向量的大小,箭头的方向表示向量的方向。
二、平面向量的运算法则1. 向量的加法:将两个向量的起点放在一起,然后将两个箭头相连,连接结果的箭头即为两个向量相加的结果。
2. 向量的减法:将两个向量的起点放在一起,然后将第二个向量取反,再按向量加法的法则进行运算。
3. 向量的数乘:将向量的长度与一个数相乘,结果的方向保持不变,只改变了大小。
三、平面向量的性质1. 平面向量的相等:两个向量的大小和方向完全相同,则它们是相等的。
2. 平面向量的负向量:具有相同大小但方向相反的向量称为原向量的负向量。
3. 平面向量的数量积:两个向量的数量积等于两个向量的模长的乘积与它们夹角的余弦值的乘积。
4. 平面向量的夹角:两个向量的夹角是一个锐角,它与它们的余弦值有关。
5. 平面向量的线性相关与线性无关:若存在不全为零的实数使得向量的线性组合等于零向量,则称这些向量线性相关;否则称这些向量线性无关。
四、平面向量的坐标表示1. 平面向量的坐标表示方法:平面向量可以用有序数对或者列向量来表示。
2. 平面向量的坐标运算:平面向量的加法、减法和数乘运算可以通过对应元素之间的运算来进行。
五、平面向量的标准表示1. 平面向量的标准表示方法:平面向量可以表示为单位向量与它的长度的乘积。
2. 平面向量的标准化:将向量除以它的模长,使其成为单位向量。
六、平面向量的数量积1. 平面向量的数量积的计算:将两个向量的对应坐标相乘,再将相乘结果相加。
2. 平面向量的数量积与夹角:两个向量的数量积等于它们的模长的乘积与它们的夹角的余弦值的乘积。
以上是平面向量的一些基本概念、运算法则、性质和表示方法的梳理。
通过学习平面向量,我们可以更好地理解和应用向量的概念,并在几何问题中进行计算和推导。

平面向量的概念及线性运算【考点梳理】1.向量的有关概念(1)向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的长度(或模).(2)零向量:长度为0的向量,其方向是任意的.(3)单位向量:长度等于1个单位的向量.(4)平行向量:方向相同或相反的非零向量.平行向量又叫共线向量.规定:0与任一向量平行.(5)相等向量:长度相等且方向相同的向量.(6)相反向量:长度相等且方向相反的向量.2.向量的线性运算向量运算定义法则(或几何意义)运算律加法求两个向量和的运算三角形法则平行四边形法则(1)交换律:a+b=b+a;(2)结合律:(a+b)+c=a+(b+c)减法求a与b的相反向量-b的和的运算叫做a与b的差三角形法则a-b=a+(-b)数乘求实数λ与向量a的积的运算(1)|λa|=|λ||a|;(2)当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向相λ(μa)=λμa;(λ+μ)a=λa+μa;λ(a+b)=λa+λb3.共线向量定理向量a (a ≠0)与b 共线的充要条件是存在唯一一个实数λ,使得b =λa . 【考点突破】考点一、平面向量的有关概念【例1】给出下列四个命题: ①若|a |=|b |,则a =b ;②若A ,B ,C ,D 是不共线的四点,则“AB →=DC →”是“四边形ABCD 为平行四边形”的充要条件;③若a =b ,b =c ,则a =c ; ④a =b 的充要条件是|a |=|b |且a ∥b . 其中正确命题的序号是( )A .②③B .①②C .③④D .②④ [答案] A[解析] ①不正确.两个向量的长度相等,但它们的方向不一定相同.②正确.∵AB →=DC →,∴|AB →|=|DC →|且AB →∥DC →,又A ,B ,C ,D 是不共线的四点,∴四边形ABCD 为平行四边形;反之,若四边形ABCD 为平行四边形,则|AB →|=|DC →|,AB →∥DC →且AB →,DC →方向相同,因此AB →=DC →.③正确.∵a =b ,∴a ,b 的长度相等且方向相同,又b =c ,∴b ,c 的长度相等且方向相同,∴a ,c 的长度相等且方向相同,故a =c .④不正确.当a ∥b 且方向相反时,即使|a |=|b |,也不能得到a =b ,故|a |=|b |且a ∥b 不是a =b 的充要条件,而是必要不充分条件.综上所述,正确命题的序号是②③. 【类题通法】1.相等向量具有传递性,非零向量的平行也具有传递性.2.共线向量即为平行向量,它们均与起点无关.3.向量可以平移,平移后的向量与原向量是相等向量.解题时,不要把它与函数图象的移动混为一谈.4.非零向量a 与a |a |的关系:a|a |是与a 同方向的单位向量. 【对点训练】 给出下列六个命题:①若|a |=|b |,则a =b 或a =-b ; ②若AB →=DC →,则ABCD 为平行四边形; ③若a 与b 同向,且|a |>|b |,则a >b ; ④λ,μ为实数,若λa =μb ,则a 与b 共线; ⑤λa =0(λ为实数),则λ必为零;⑥a ,b 为非零向量,a =b 的充要条件是|a |=|b |且a ∥b . 其中假命题的序号为________. [答案] ①②③④⑤⑥[解析] ①不正确.|a |=|b |.但a ,b 的方向不确定,故a ,b 不一定是相等或相反向量;②不正确.因为AB →=DC →,A ,B ,C ,D 可能在同一直线上,所以ABCD 不一定是四边形.③不正确.两向量不能比较大小.④不正确.当λ=μ=0时,a 与b 可以为任意向量,满足λa =μb ,但a 与b 不一定共线.⑤不正确.当λ=1,a =0时,λa =0.⑥不正确.对于非零向量a ,b ,a =b 的充要条件是|a |=|b |且a ,b 同向.考点二、平面向量的线性运算【例2】(1) 设D 为△ABC 所在平面内一点,AD →=-13AB →+43AC →,若BC →=λDC →(λ∈R ),则λ=( )A .2B .3C .-2D .-3(2)在△ABC 中,点M ,N 满足AM →=2MC →,BN →=NC →.若MN →=xAB →+yAC →,则x =________;y =________.[答案] (1)D (2)12 -16[解析] (1)由AD →=-13AB →+43AC →,可得3AD →=-AB →+4AC →,即4AD →-4AC →=AD →-AB →,则4CD →=BD →,即BD →=-4DC →,可得BD →+DC →=-3DC →,故BC →=-3DC →,则λ=-3.(2)由题中条件得,MN →=MC →+CN →=13AC →+12CB →=13AC →+12(AB →-AC →)=12AB →-16AC →=xAB →+yAC →,所以x =12,y =-16.【类题通法】1.解题的关键在于熟练地找出图形中的相等向量,并能熟练运用相反向量将加减法相互转化.2.用几个基本向量表示某个向量问题的基本技巧:(1)观察各向量的位置;(2)寻找相应的三角形或多边形;(3)运用法则找关系;(4)化简结果.【对点训练】1.已知D 为三角形ABC 边BC 的中点,点P 满足P A →+BP →+CP →=0,AP →=λPD →,则实数λ的值为________.[答案] -2[解析] 因为D 是BC 的中点,则AB →+AC →=2AD →.由P A →+BP →+CP →=0,得BA →=PC →. 又AP →=λPD →,所以点P 是以AB ,AC 为邻边的平行四边形的第四个顶点,因此AP →=AB →+AC →=2AD →=-2PD →,所以λ=-2.2.设D ,E 分别是△ABC 的边AB ,BC 上的点,AD =12AB ,BE =23BC .若DE →=λ1AB →+λ2AC →(λ1,λ2为实数),则λ1+λ2的值为________.[答案] 12[解析] DE →=DB →+BE →=12AB →+23BC →=12AB →+23(AC →-AB →)=-16AB →+23AC →,∵DE →=λ1AB →+λ2AC →,∴λ1=-16,λ2=23,因此λ1+λ2=12.考点三、共线向量定理的应用【例3】(1)已知向量AB →=a +3b ,BC →=5a +3b ,CD →=-3a +3b ,则( ) A .A ,B ,C 三点共线 B .A ,B ,D 三点共线 C .A ,C ,D 三点共线 D .B ,C ,D 三点共线(2)已知向量a ,b 不共线,且c =λa +b ,d =a +(2λ-1)b ,若c 与d 共线反向,则实数λ的值为( )A .1B .-12C .1或-12 D .-1或-12[答案] (1) B (2) B[解析] (1)∵BD →=BC →+CD →=2a +6b =2(a +3b )=2AB →, ∴BD →,AB →共线,又有公共点B , ∴A ,B ,D 三点共线.故选B.(2)由于c 与d 共线反向,则存在实数k 使 c =k d (k <0),于是λa +b =k [a +(2λ-1)b ]. 整理得λa +b =k a +(2λk -k )b .由于a ,b 不共线,所以有⎩⎨⎧λ=k ,2λk -k =1,整理得2λ2-λ-1=0,解得λ=1或λ=-12.又因为k <0,所以λ<0,故λ=-12.【类题通法】 共线向量定理的应用(1)证明向量共线:对于向量a ,b ,若存在实数λ,使a =λb ,则a 与b 共线. (2)证明三点共线:若存在实数λ,使AB →=λAC →,则A ,B ,C 三点共线. (3)求参数的值:利用共线向量定理及向量相等的条件列方程(组)求参数的值. 【对点训练】1.向量e 1,e 2不共线,AB →=3(e 1+e 2),CB →=e 2-e 1,CD →=2e 1+e 2,给出下列结论:①A ,B ,C 共线;②A ,B ,D 共线;③B ,C ,D 共线;④A ,C ,D 共线,其中所有正确结论的序号为________.[答案] ④[解析] 由AC →=AB →-CB →=4e 1+2e 2=2CD →,且AB →与CB →不共线,可得A ,C ,D 共线,且B 不在此直线上.2.设向量a ,b 不平行,向量λa +b 与a +2b 平行,则实数λ=________. [答案] 12[解析] ∵λa +b 与a +2b 平行,∴λa +b =t (a +2b ),即λa +b =t a +2t b ,∴⎩⎨⎧λ=t ,1=2t ,解得⎩⎪⎨⎪⎧λ=12,t =12.。
初中数学知识归纳平面向量的线性运算及应用初中数学知识归纳:平面向量的线性运算及应用一、引言初中数学中,线性运算是一个重要的概念。
在平面几何中,平面向量的线性运算是一种常见且有用的运算。
本文将归纳总结平面向量的线性运算及其应用。
二、平面向量的定义与表示平面向量是具有大小和方向的量,用有向线段表示。
在直角坐标系中,平面向量可以用坐标表示为:AB = (x, y)其中,x表示与x轴的水平距离,y表示与y轴的垂直距离。
三、平面向量的线性运算1. 平面向量的加法若有两个平面向量AB = (x₁, y₁)和CD = (x₂, y₂),则它们的和为:AB + CD = (x₁ + x₂, y₁ + y₂)2. 平面向量的数乘若有一个平面向量AB = (x, y)和一个实数k,那么它们的数乘为:kAB = (kx, ky)3. 平面向量的减法若有两个平面向量AB = (x₁, y₁)和CD = (x₂, y₂),则它们的差为:AB - CD = (x₁ - x₂, y₁ - y₂)4. 平面向量的线性组合若有n个平面向量A₁, A₂, ..., An和n个实数k₁, k₂, ..., kn,则它们的线性组合为:k₁A₁ + k₂A₂ + ... + knAn四、平面向量的应用1. 平行向量两个向量的方向相同或相反时,它们为平行向量。
在平行四边形的性质中,平行向量具有重要的应用。
2. 向量共线与共面若有三个点A,B,C构成的两个向量AB和AC共线,则三个点A,B,C共线。
若两个向量在同一个平面内,它们为共面向量。
3. 向量的模长与方向角平面向量的模长为向量的长度,用|AB|表示。
向量的方向角为向量与水平方向的夹角,一般用α表示。
4. 平面向量的投影平面向量的投影表示一个向量在另一个向量上的投影长度,应用于解决几何问题中的投影性质。
5. 平面向量的线性相关与线性无关若存在一组实数k₁, k₂, ..., kn,使得k₁A₁ + k₂A₂ + ... + knAn = 0且不全为0,则这组向量为线性相关向量。
平面向量的线性运算平面向量是解决平面几何问题的重要工具。
平面向量之间可以进行线性运算,包括加减法、数量乘法和应用特殊运算规则的向量乘法。
本文将详细介绍平面向量的线性运算及其应用。
一、平面向量的基本概念在平面直角坐标系中,向量由两个有序实数对表示,分别表示向量在 x 轴和 y 轴上的分量。
设向量 a 的分量为 (a1, a2),则向量 a 可表示为 a = a1i + a2j,其中 i 和 j 分别是 x 轴和 y 轴的单位向量。
二、平面向量的加法设有两个平面向量 a = a1i + a2j, b = b1i + b2j,其和为 c = (a1 +b1)i + (a2 + b2)j。
向量的加法满足交换律、结合律和零向量的存在性。
三、平面向量的减法设有两个平面向量 a = a1i + a2j, b = b1i + b2j,其差为 c = (a1 - b1)i + (a2 - b2)j。
向量的减法也满足交换律和结合律。
四、平面向量的数量乘法设有平面向量 a = a1i + a2j,实数 k,k与向量 a 的数量积为 k * a =ka1i + ka2j。
数量乘法满足结合律、分配律和对数乘法的分布律等性质。
五、平面向量的线性运算应用1. 向量共线与平行若有两个非零向量 a 和 b,当且仅当存在实数 k,使得 a = kb,称向量 a 和 b 共线。
若向量 a 和 b 共线且方向相同或相反,则称向量 a 和b 平行。
2. 向量的线性组合设有向量组 a1, a2, ..., an,其中每个向量的形式为 ai = ai1i + ai2j。
对于任意给定的实数 k1, k2, ..., kn,向量 b = k1a1 + k2a2 + ... + knan 称为向量组 a1, a2, ..., an 的线性组合。
3. 向量的共面性若存在不全为零的实数 k1, k2, k3,使得 k1a1 + k2a2 + k3a3 = 0,称向量组 a1, a2, a3 共面。
平面向量知识点归纳一、平面向量的基本概念1、向量既有大小又有方向的量叫做向量。
物理学中又称为矢量。
向量可以用有向线段来表示,有向线段的长度表示向量的大小,箭头所指的方向表示向量的方向。
2、向量的模向量的大小叫做向量的模,记作|a|。
3、零向量长度为 0 的向量叫做零向量,记作 0 。
零向量的方向是任意的。
4、单位向量长度等于 1 个单位长度的向量叫做单位向量。
5、平行向量(共线向量)方向相同或相反的非零向量叫做平行向量,也叫共线向量。
规定:零向量与任意向量平行。
6、相等向量长度相等且方向相同的向量叫做相等向量。
7、相反向量长度相等且方向相反的向量叫做相反向量。
二、平面向量的线性运算1、向量的加法(1)三角形法则已知非零向量 a、b,在平面内任取一点 A,作 AB = a,BC = b,则向量 AC 叫做 a 与 b 的和,记作 a + b ,即 a + b = AB + BC =AC 。
(2)平行四边形法则已知两个不共线的向量 a、b,作 AB = a,AD = b,以 AB、AD 为邻边作平行四边形 ABCD,则对角线 AC 就是 a 与 b 的和,记作 a +b 。
(3)向量加法的运算律交换律:a + b = b + a结合律:(a + b) + c = a +(b + c)2、向量的减法(1)相反向量与向量 a 长度相等,方向相反的向量叫做 a 的相反向量,记作 a 。
(2)向量的减法向量 a 加上 b 的相反向量,叫做 a 与 b 的差,即 a b = a +(b) 。
3、向量的数乘(1)定义实数λ与向量 a 的积是一个向量,记作λa ,它的长度与方向规定如下:①|λa| =|λ|·|a| ;②当λ>0 时,λa 的方向与 a 的方向相同;当λ<0 时,λa 的方向与 a 的方向相反;当λ = 0 时,λa = 0 。
(2)运算律结合律:λ(μa) =(λμ)a分配律:(λ +μ)a =λa +μa ,λ(a + b) =λa +λb三、平面向量的坐标表示1、在平面直角坐标系中,分别取与 x 轴、y 轴方向相同的两个单位向量 i、j 作为基底。
平面向量的概念及线性运算考点与提醒归纳一、基础知识1.向量的有关概念(1)向量的定义及表示:既有大小又有方向的量叫做向量.以A 为起点、B 为终点的向量记作AB ―→,也可用黑体的单个小写字母a ,b ,c ,…来表示向量.(2)向量的长度(模):向量AB ―→的大小即向量AB ―→的长度(模),记为|AB ―→|. 2.几种特殊向量 名称 定义 备注零向量 长度为0的向量 零向量记作0,其方向是任意的 单位向量长度等于1个单位的向量 单位向量记作a 0,a 0=a|a |平行向量方向相同或相反的非零向量(也叫共线向量)0与任意向量共线相等向量 长度相等且方向相同的向量 相等向量一定是平行向量,平行向量不一定是相等向量相反向量 长度相等且方向相反的两个向量若a ,b 为相反向量,则a =-b单位向量有无数个,它们大小相等,但方向不一定相同;与向量a 平行的单位向量有两个,即向量a|a |和-a|a |.3.向量的线性运算 向量运算定义 法则(或几何意义)运算律加法求两个向量和的运算三角形法则 平行四边形法则❷(1)交换律:a +b =b +a ; (2)结合律:(a +b )+c =a +(b +c )减法求a 与b的相反向a -b =a +(-b )量-b 的和的运算叫做a 与b 的差 三角形法则数乘求实数λ与向量a 的积的运算|λa |=|λ||a |;当λ>0时,λa 的方向与a 的方向相同;当λ<0时,λa 的方向与a 的方向相反;当λ=0时,λa =0λ(μa )=(λμ)a ;(λ+μ)a =λa +μa ;λ(a +b )=λa +λb❷向量加法的多边形法则多个向量相加,利用三角形法则,应首尾顺次连接,a +b +c 表示从始点指向终点的向量,只关心始点、终点.4.共线向量定理向量a (a ≠0)与b 共线,当且仅当有唯一一个实数λ,使得b =λa . 只有a ≠0才保证实数λ的存在性和唯一性.二、常用结论(1)若P 为线段AB 的中点,O 为平面内任一点,则OP ―→=12(OA ―→+OB ―→).(2)OA ―→=λOB ―→+μOC ―→(λ,μ为实数),若点A ,B ,C 三点共线,则λ+μ=1.考点一 平面向量的有关概念[典例] 给出下列命题: ①若a =b ,b =c ,则a =c ;②若A ,B ,C ,D 是不共线的四点,则AB ―→=DC ―→是四边形ABCD 为平行四边形的充要条件;③a =b 的充要条件是|a |=|b |且a ∥b ; ④若a ∥b ,b ∥c ,则a ∥c .其中正确命题的序号是________.[解析] ①正确.∵a =b ,∴a ,b 的长度相等且方向相同, 又b =c ,∴b ,c 的长度相等且方向相同, ∴a ,c 的长度相等且方向相同,故a =c .②正确.∵AB ―→=DC ―→,∴|AB ―→|=|DC ―→|且AB ―→∥DC ―→, 又A ,B ,C ,D 是不共线的四点, ∴四边形ABCD 为平行四边形; 反之,若四边形ABCD 为平行四边形, 则AB ―→∥DC ―→且|AB ―→|=|DC ―→|,因此,AB ―→=DC ―→.③不正确.当a ∥b 且方向相反时,即使|a |=|b |,也不能得到a =b ,故|a |=|b |且a ∥b 不是a =b 的充要条件,而是必要不充分条件.④不正确.考虑b =0这种特殊情况. 综上所述,正确命题的序号是①②. [答案] ①②[解题技法] 向量有关概念的关键点 (1)向量定义的关键是方向和长度.(2)非零共线向量的关键是方向相同或相反,长度没有限制. (3)相等向量的关键是方向相同且长度相等. (4)单位向量的关键是长度都是一个单位长度.(5)零向量的关键是长度是0,规定零向量与任意向量共线. [题组训练] 1.给出下列命题:①两个具有公共终点的向量,一定是共线向量; ②λa =0(λ为实数),则λ必为零;③λ,μ为实数,若λa =μb ,则a 与b 共线. 其中错误的命题的个数为( ) A .0 B .1 C .2D .3解析:选D ①错误,两向量共线要看其方向而不是起点或终点.②错误,当a =0时,不论λ为何值,λa =0.③错误,当λ=μ=0时,λa =μb =0,此时,a 与b 可以是任意向量.故错误的命题有3个,故选D.2.设a 0为单位向量,下列命题中:①若a 为平面内的某个向量,则a =|a |·a 0;②若a 与a 0平行,则a =|a |a 0;③若a 与a 0平行且|a |=1,则a =a 0,假命题的个数是( )A .0B .1C .2D .3解析:选D 向量是既有大小又有方向的量,a 与|a |a 0的模相同,但方向不一定相同,故①是假命题;若a 与a 0平行,则a 与a 0的方向有两种情况:一是同向,二是反向,反向时a =-|a |a 0,故②③也是假命题.综上所述,假命题的个数是3.考点二 平面向量的线性运算[典例] (1)(2018·全国卷Ⅰ)在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB ―→=( )A.34AB ―→-14AC ―→B.14AB ―→-34AC ―→C.34AB ―→+14AC ―→ D.14AB ―→+34AC ―→(2)如图,在直角梯形ABCD 中,DC ―→=14AB ―→,BE ―→=2EC ―→, 且AE ―→=r AB ―→+s AD ―→,则2r +3s =( )A .1B .2C .3D .4[解析] (1)作出示意图如图所示.EB ―→=ED ―→+DB ―→=12AD ―→+12CB ―→=12×12(AB ―→+AC ―→)+12(AB ―→-AC ―→)=34AB ―→-14AC ―→.故选A. (2)根据图形,由题意可得AE ―→=AB ―→+BE ―→=AB ―→+23BC ―→=AB ―→+23(BA ―→+AD ―→+DC ―→)=13AB ―→+23(AD ―→+DC ―→)=13AB ―→+23⎝⎛⎭⎫AD ―→+14AB ―→=12AB ―→+23AD ―→.因为AE ―→=r AB ―→+s AD ―→,所以r =12,s =23,则2r +3s =1+2=3.[答案] (1)A (2)C[解题技法] 向量线性运算的解题策略(1)常用的法则是平行四边形法则和三角形法则,一般共起点的向量求和用平行四边形法则,求差用三角形法则,求首尾相连的向量的和用三角形法则.(2)找出图形中的相等向量、共线向量,将所求向量与已知向量转化到同一个平行四边形或三角形中求解.(3)用几个基本向量表示某个向量问题的基本技巧:①观察各向量的位置;②寻找相应的三角形或多边形;③运用法则找关系;④化简结果. (4)与向量的线性运算有关的参数问题,一般是构造三角形,利用向量运算的三角形法则进行加法或减法运算,然后通过建立方程组即可求得相关参数的值.[题组训练]1.设D 为△ABC 所在平面内一点,BC ―→=3CD ―→,则( ) A .AD ―→=-13AB ―→+43AC ―→B .AD ―→=13AB ―→-43AC ―→C .AD ―→=43AB ―→+13AC ―→D .AD ―→=43AB ―→-13AC ―→解析:选A 由题意得AD ―→=AC ―→+CD ―→=AC ―→+13BC ―→=AC ―→+13AC ―→-13AB ―→=-13AB ―→+43AC ―→. 2.(2019·太原模拟)在正方形ABCD 中,M ,N 分别是BC ,CD 的中点,若AC ―→=λAM ―→+μAN ―→,则实数λ+μ=________.解析:如图,∵AM ―→=AB ―→+BM ―→=AB ―→+12BC ―→=DC ―→+12BC ―→,①AN ―→=AD ―→+DN ―→=BC ―→+12DC ―→,②由①②得BC ―→=43AN ―→-23AM ―→,DC ―→=43AM ―→-23AN ―→,∴AC ―→=AB ―→+BC ―→=DC ―→+BC ―→=43AM ―→-23AN ―→+43AN ―→-23AM ―→=23AM ―→+23AN ―→,∵AC ―→=λAM ―→+μAN ―→,∴λ=23,μ=23,λ+μ=43.答案:43考点三 共线向量定理的应用[典例] 设两个非零向量a 与b 不共线,(1)若AB ―→=a +b ,BC ―→=2a +8b ,CD ―→=3a -3b , 求证:A ,B ,D 三点共线;(2)试确定实数k ,使k a +b 和a +k b 同向.[解] (1)证明:∵AB ―→=a +b ,BC ―→=2a +8b ,CD ―→=3a -3b , ∴BD ―→=BC ―→+CD ―→=2a +8b +3a -3b =5(a +b )=5AB ―→, ∴AB ―→,BD ―→共线. 又∵它们有公共点B , ∴A ,B ,D 三点共线. (2)∵k a +b 与a +k b 同向,∴存在实数λ(λ>0),使k a +b =λ(a +k b ), 即k a +b =λa +λk b . ∴(k -λ)a =(λk -1)b .∵a ,b 是不共线的非零向量,∴⎩⎪⎨⎪⎧ k -λ=0,λk -1=0,解得⎩⎪⎨⎪⎧ k =1,λ=1或⎩⎪⎨⎪⎧k =-1,λ=-1, 又∵λ>0,∴k =1.1.向量共线问题的注意事项(1)向量共线的充要条件中,当两向量共线时,通常只有非零向量才能表示与之共线的其他向量,注意待定系数法和方程思想的运用.(2)证明三点共线问题,可用向量共线来解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得到三点共线.[题组训练]1.在四边形ABCD 中,AB ―→=a +2b ,BC ―→=-4a -b ,CD ―→=-5a -3b ,则四边形ABCD 的形状是( )A .矩形B .平行四边形C .梯形D .以上都不对解析:选C 由已知,得AD ―→=AB ―→+BC ―→+CD ―→=-8a -2b =2(-4a -b )=2BC ―→,故AD ―→∥BC ―→.又因为AB ―→与CD ―→不平行,所以四边形ABCD 是梯形.2.已知向量e 1≠0,λ∈R ,a =e 1+λe 2,b =2e 1,若向量a 与向量b 共线,则( ) A .λ=0 B .e 2=0 C .e 1∥e 2D .e 1∥e 2或λ=0解析:选D 因为向量e 1≠0,λ∈R ,a =e 1+λe 2,b =2e 1,又因为向量a 和b 共线,存在实数k ,使得a =k b ,所以e 1+λe 2=2k e 1,所以λe 2=(2k -1)e 1,所以e 1∥e 2或λ=0.3.已知O 为△ABC 内一点,且AO ―→=12(OB ―→+OC ―→),AD ―→=t AC ―→,若B ,O ,D 三点共线,则t =( )A.14B.13C.12D.23解析:选B 设E 是BC 边的中点,则12(OB ―→+OC ―→)=OE ―→,由题意得AO ―→=OE ―→,所以AO ―→=12AE ―→=14(AB ―→+AC ―→)=14AB ―→+14t AD ―→,又因为B ,O ,D 三点共线,所以14+14t =1,解得t =13,故选B.4.已知O ,A ,B 三点不共线,P 为该平面内一点,且OP ―→=OA ―→+AB―→|AB ―→|,则( )A .点P 在线段AB 上 B .点P 在线段AB 的延长线上C .点P 在线段AB 的反向延长线上D .点P 在射线AB 上解析:选D 由OP ―→=OA ―→+AB ―→|AB ―→|,得OP ―→-OA ―→=AB ―→|AB ―→|,∴AP ―→=1|AB ―→|·AB ―→,∴点P 在射线AB 上,故选D.[课时跟踪检测]1.设D ,E ,F 分别为△ABC 的三边BC ,CA ,AB 的中点,则EB ―→+FC ―→=( ) A .AD ―→B.12AD ―→C.12BC ―→ D .BC ―→解析:选A 由题意得EB ―→+FC ―→=12(AB ―→+CB ―→)+12(AC ―→+BC ―→)=12(AB ―→+AC ―→)=AD ―→.2.已知向量a ,b 不共线,且c =λa +b ,d =a +(2λ-1)b ,若c 与d 共线反向,则实数λ的值为( )A .1B .-12C .1或-12D .-1或-12解析:选B 由于c 与d 共线反向,则存在实数k 使c =kd (k <0), 于是λa +b =k []a +(2λ-1)b . 整理得λa +b =k a +(2λk -k )b .由于a ,b 不共线,所以有⎩⎪⎨⎪⎧λ=k ,2λk -k =1,整理得2λ2-λ-1=0,解得λ=1或λ=-12.又因为k <0,所以λ<0,故λ=-12.3.设向量a ,b 不共线,AB ―→=2a +p b ,BC ―→=a +b ,CD ―→=a -2b ,若A ,B ,D 三点共线,则实数p 的值为( )A .-2B .-1C .1D .2解析:选B 因为BC ―→=a +b ,CD ―→=a -2b ,所以BD ―→=BC ―→+CD ―→=2a -b .又因为A ,B ,D 三点共线,所以AB ―→,BD ―→共线.设AB ―→=λBD ―→,所以2a +p b =λ(2a -b ),所以2=2λ,p =-λ,即λ=1,p =-1.4.(2019·甘肃诊断)设D 为△ABC 所在平面内一点,BC ―→=-4CD ―→,则AD ―→=( ) A.14AB ―→-34AC ―→ B.14AB ―→+34AC ―→C.34AB ―→-14AC ―→D.34AB ―→+14AC ―→解析:选B 法一:设AD ―→=x AB ―→+y AC ―→,由BC ―→=-4CD ―→可得,BA ―→+AC ―→=-4CA―→-4AD ―→,即-AB ―→-3AC ―→=-4x AB ―→-4y AC ―→,则⎩⎪⎨⎪⎧-4x =-1,-4y =-3,解得⎩⎨⎧x =14,y =34,即AD ―→=14AB ―→+34AC ―→,故选B. 法二:在△ABC 中,BC ―→=-4CD ―→,即-14BC ―→=CD ―→,则AD ―→=AC ―→+CD ―→=AC ―→-14BC―→=AC ―→-14(BA ―→+AC ―→)=14AB ―→+34AC ―→,故选B.5.在平面直角坐标系中,O 为坐标原点,A ,B ,C 三点满足OC ―→=34OA ―→+14OB ―→,则|BC ―→||AC ―→|等于( )A .1B .2C .3D.32解析:选C 因为BC ―→=OC ―→-OB ―→=34OA ―→+14OB ―→-OB ―→=34BA ―→,AC ―→=OC ―→-OA ―→=34OA ―→+14OB ―→-OA ―→=14AB ―→,所以|BC ―→||AC ―→|=3.故选C.6.已知△ABC 的边BC 的中点为D ,点G 满足GA ―→+BG ―→+CG ―→=0,且AG ―→=λGD ―→,则λ的值是( )A.12 B .2 C .-2D .-12解析:选C 由GA ―→+BG ―→+CG ―→=0,得G 为以AB ,AC 为邻边的平行四边形的第四个顶点,因此AG ―→=-2GD ―→,则λ=-2.故选C.7.下列四个结论:①AB ―→+BC ―→+CA ―→=0;②AB ―→+MB ―→+BO ―→+OM ―→=0; ③AB ―→-AC ―→+BD ―→-CD ―→=0;④N Q ―→+Q P ―→+MN ―→-MP ―→=0,其中一定正确的结论个数是( ) A .1 B .2 C .3D .4解析:选C ①AB ―→+BC ―→+CA ―→=AC ―→+CA ―→=0,①正确;②AB ―→+MB ―→+BO ―→+OM ―→=AB ―→+MO ―→+OM ―→=AB ―→,②错误;③AB ―→-AC ―→+BD ―→-CD ―→=CB ―→+BD ―→+DC ―→=CD ―→+DC ―→=0,③正确;④N Q ―→+Q P ―→+MN ―→-MP ―→=NP ―→+PN ―→=0,④正确.故①③④正确.8.如图,在平行四边形ABCD 中,M ,N 分别为AB ,AD 上的点,且AM ―→=34AB ―→,AN ―→=23AD ―→,AC ,MN 交于点P .若AP ―→=λAC ―→,则λ的值为( )A.35B.37C.316D.617解析:选D ∵AM ―→=34AB ―→,AN ―→=23AD ―→,∴AP ―→=λAC ―→=λ(AB ―→+AD ―→)=λ⎝⎛⎭⎫43AM ―→+32AN ―→=43λAM ―→+32λAN ―→.∵点M ,N ,P 三点共线,∴43λ+32λ=1,则λ=617.故选D. 9.设向量a ,b 不平行,向量λa +b 与a +2b 平行,则实数λ=________. 解析:因为向量λa +b 与a +2b 平行,所以可设λa +b =k (a +2b ),则⎩⎪⎨⎪⎧λ=k ,1=2k ,所以λ=12.答案:1210.若AP ―→=12PB ―→,AB ―→=(λ+1)BP ―→,则λ=________.解析:如图,由AP ―→=12PB ―→,可知点P 是线段AB 上靠近点A 的三等分点,则AB ―→=-32BP ―→,结合题意可得λ+1=-32,所以λ=-52.答案:-5211.已知平行四边形ABCD 的对角线AC 和BD 相交于O ,且OA ―→=a ,OB ―→=b ,则DC―→。