工程制图相贯线的画法
- 格式:ppt
- 大小:8.17 MB
- 文档页数:6

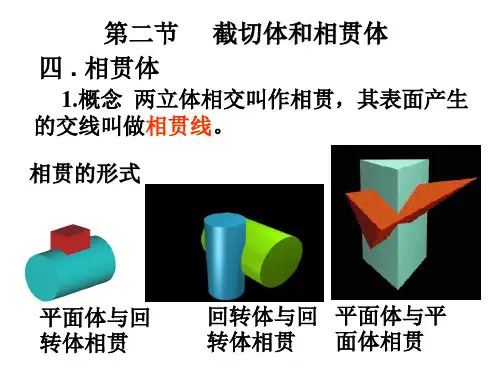







一、概述两立体表面的交线称为相贯线,见图5-14a和b所示的三通管和盖。
三通管是由水平横放的圆筒与垂直竖放的带孔圆锥台组合而成。
盖是由水平横放的圆筒与垂直竖放的带孔圆锥台、圆筒组合而成。
它们的表面(外表面或表面)相交,均出现了箭头所指的相贯线,在画该类零件的投影图时,必然涉及绘制相贯线的投影问题。
讨论两立体相交的问题,主要是讨论如何求相贯线。
工程图上画出两立体相贯线的意义,在于用它来完善、清晰地表达出零件各部分的形状和相对位置,为准确地制造该零件提供条件。
(一)相贯线的性质由于组成相贯体的各立体的形状、大小和相对位置的不同,相贯线也表现为不同的形状,但任何两立体表面相交的相贯线都具有下列基本性质:1.共有性相贯线是两相交立体表面的共有线,也是两立体表面的分界线,相贯线上的点一定是两相交立体表面的共有点。
2.封闭性由于形体具有一定的空间围,所以相贯线一般都是封闭的。
在特殊情况下还可能是不封闭的,如图5-15c所示。
3.相贯线的形状平面立体与平面立体相交,其相贯线为封闭的空间折线或平面折线。
平面立体与曲面立体相交,其相贯线为由若干平面曲线或平面曲线和直线结合而成的封闭的空间的几何形。
应该指出:由于平面立体与平面立体相交或平面立体与曲面立体相交,都可以理解为平面与平面立体或平面与曲面立体相交的截交情况,因此,相贯的主要形式是曲面立体与曲面立体相交。
最常见的曲面立体是回转体。
两回转体相交,其相贯线一般情况下是封闭的空间曲线(如图5-15a),特殊情况下是平面曲线(如图5-15 b)或由直线和平面曲线组成(如图5-15c ).(二)求相贯线的方法、步骤求画两回转体的相贯线,就是要求出相贯线上一系列的共有点。
求共有点的方法有:面上取点法、辅助平面法和辅助同心球面法。
具体作图步骤为:(1)找出一系列的特殊点(特殊点包括:极限位置点、转向点、可见性分界点);(2)求出一般点;(3)判别可见性;(4)顺次连接各点的同面投影;(5)整理轮廓线。