工程制图(截交线和相贯线)习题解答
- 格式:pps
- 大小:402.00 KB
- 文档页数:20

截交、相贯习题课⏹第一题⏹第二题⏹第三题⏹第四题⏹第五题⏹第六题第七题第八题第九题第十题第十一题第十二题第十三题第十四题第十五题1.补全主、俯视图中所缺的图线。
2.补全左视图中所缺的图线。
3.补全俯视图和左视图中所缺的图线。
1’(2’)212’’1’’3’(4’)4’’3’’5’5’’⑴读三视图,想象物体及截交线的形状。
⑵求截交线。
⑶补全棱线。
123454.补全俯视图和左视图中所缺的图线。
1’12’3’(4’)2341’’(4’’)3’’2’’6’5’55’’6’’6⑴读三视图,想象立体及截交线形状。
⑵逐条作出截交线。
⑶补全轮廓线的投影。
1234565.补全主视图中所缺的图线。
11’2(3)3’2’4(5)4’5’67(8)9(10)3’’2’’4’’5’’7’’8’’9’’10’’10’9’8’7’6’⑴读图想象立体及截交线的形状。
⑵分别画出各段截交线。
轮廓线投影交线6.补全俯视图和左视图中所缺的图线。
1’(2’)1’’2’’123’34’(5’)456’6’’4’’5’’7’(8’)878’’7’’⑴读图想象立体及截交线的形状。
⑵分别画出各段截交线。
⑶补全轮廓线。
7.补全俯视图和左视图中所缺的图线。
①读图想象立体和截交线形状。
②画出各段截交线③调整轮廓线。
8.补水平投影和侧面投影。
⑴读图想象立体及截交线的形状⑵分别画出各段截交线。
⑶调整轮廓线。
返回9.补水平投影和侧面投影。
1'3'2'4'12341''2''3''4''①读图想象立体和相贯线的形状。
②利用积聚性找出相贯线的已知投影并找出特殊点。
返回10.补全水平投影。
1'2'(3')4'(5')6'(7')8'(9')10'10647891235①读图想象立体和相贯线的形状。



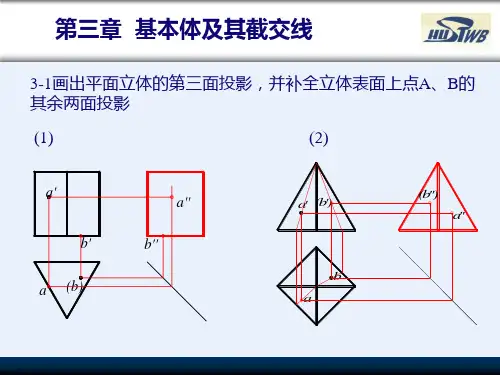
第五节截交线与相贯线【2 】截交线和相贯线是立体表面常见的两种表面交线,立体被平面截切,表面就会产生截交线,两立体订交,表面就产生相贯线,二者有配合点,也有不同点.一.截交线的特点及画法【考纲领求】1、控制特别地位平面截断棱柱和棱锥的截交线画法;2、控制特别地位平面截断圆柱.圆锥.圆球的截交线画法;3、控制简略的同轴反转展转体的截交线画法;【要点精讲】(一)截交线的界说:由平面截断根本体所形成的表面交线称为截交线.(二)截交线的特点:1.任何根本体的截交线都是一个关闭的平面图形(平面体是平面多边形,曲面体是平面曲线或由平面曲线与直线配合构成的图形);2.截交线是截平面与根本体表面的共有线,截交线上的每一点都是截平面与根本体表面的共有点(共有点的聚集).(三)求截交线的办法:①积累性求点法;②帮助(素)线法;③帮助平面法.(四)求截交线的步骤:1.肯定被截断的根本体的几何外形;2.断定截平面的截断根本体的地位(反转展转体判别截平面与轴线的相对地位3.想象截交线的空间外形;4.剖析截平面与投影面的相对地位,弄清截交线的投影特点;5.判别截交线的可见性,肯定求截交线的办法;6.将求得的各点衔接,画出其三面投影.(五)平面体的特别截交线及画法:1.特点:平面体的截交线都是由直线所构成的关闭的平面多边形.多边形的各个极点是棱线与截平面的交点,多边形的每一条边是棱面与截平面的交线.2.画法:求平面体截交线的办法主如果用积累性求点法和帮助线法.画平面体的截交线就是求出截平面与平面体上各被截棱线的交点(即平面多边形的各个极点),然后依次衔接即得截交线.依据截交线是截平面与根本体表面的共有线,截交线上的点也是截平面与根本体表面的共有点,我们所请求控制的是特别地位平面截切平面立体的截交线,我们可以应用积累性求点法或帮助平面法,求出截平面与平面立体的各棱线的交点,然后依次衔接,也就求出了截交线.例如图5-1所示,先依据截交线具有积累性投影的正面投影和具有压缩性的程度投影肯定出截平面与六棱柱棱线的六个交点(截交线平面多边形的六个极点),再应用积累性求点法求出其侧面投影.再如图5-2所示,依据截交线具有积累性的正面投影取点,再应用积累性求点法求出其程度投影和侧面投影.以上是单一截平面截断平面体所形成的截交线,当多个截平面截断平面体时,可以算作是多个截平面分离截断而组合形成的截交线,分离求出其投影,但要留意截交线的具体外形和截平面接壤处的情形.图5-1 六棱柱截交线画法图5-2 三棱锥截交线画法(六)反转展转体的特别截交线及求法:1.特点:反转展转体的截交线一般是关闭的平面曲线或由平面曲线和直线配合构成的图形.截交线上的任一点都可看作截平面与反转展转体表面上某一素线(主如果轮廓素线)或圆曲线的交点.2.类型:反转展转体的截交线比较庞杂,不同反转展转体的截交线外形是不同的.(1)单一截平面截断单一反转展转体的截交线:①圆柱的截交线:依据截平面与圆柱轴线的相对地位的不同,其截交线有三种不同的外形,如表5-1所示:表5-1 圆柱的截交线截平面的地位平行于轴线垂直于轴线竖直于轴线截交线的外形矩形圆椭圆轴测图投影图②圆锥的截交线:依据截平面与圆锥轴线的相对地位的不同,其截交线有五种不同的外形,如表5-2所示:表5-2 圆锥的截交线类别轴测图投影图截交线的外形截平面的地位1 圆垂直于轴线θ=90°2 椭圆竖直于轴线θ>α3 抛物线竖直于轴线且平行于一条素线θ=α4 双曲线平行于轴线5 过锥顶的两订交直线(三角形)竖直于轴线且过锥顶③圆球的截交线:任何地位的截平面截切圆球时,其截交都是圆.当截平面平行于某一投影面时,其投影在该投影面上的投影为一圆,在其他两个投影面上的投影都积累为直线,如图5-3所示;当截平面(投影面垂直面)垂直于某一投影面时,截交线在该投影面上的投影积累为直线,在其他两个投影面上的投影都为椭圆,如图5-4所示.图5-3 球被程度面截断5-4 球被正垂面截断(2)多个截平面截断单一反转展转体的截交线:多个截平面截断统一反转展转体的截交线可以算作多个截平面分离截断统一反转展转体而形成的截交线的组合.因为反转展转体的截交线比较庞杂,必定要肯定好截交线的具体外形,例如图5-5所示,上面的截交线是椭圆,中央的截交线是圆,下面的截交线是矩形.图5-5 圆柱被三个截平面截断图 5-6 同轴圆柱体的截交线(3)同轴反转展转体的截交线:同轴反转展转体的截交线可以算作统一截平面截断不同反转展转体所形成的截交线的组合,画同轴反转展转体的截交线时,起首要剖析该立体是由哪些根本体所构成的,再剖析截平面与每个根本体的相对地位.截交线的外形和投影特点,然后逐个画出根本体的截交线构成的图形.画图时必定要差别开截平面截断各个反转展转体的截交线外形以及各条截交线的分界点.如图5-6所示,要差别出截平面截断大圆柱和小圆柱的分界线.4、反转展转体截交线的画法:(1)求反转展转体截交线的办法:①积累性求点法;②帮助素线法;③帮助平面法.(2)投影为直线或圆的截交线画法:可以应用其积累性或真实性直接求出,如表5-1.表5-2.图5-3和图5-6所示.(3)投影为非圆曲线的截交线求法:投影为非圆曲线的截交线可依据反转展转体被截平面截断的截交线的外形,先求出截交线上特别地位点的投影(即最左.最右.最上.最下.最前.最后点,可懂得为截平面与轮廓素线或圆曲线的交点),再应用帮助平面法或表面取点法(应用积累性)求出几个一般地位点的投影(最好是对称点,求点的投影时可应用积累性求点法.帮助素线法或帮助平面法),最后滑腻衔接所求各点的同面投影即得截交线,如图5-7 a和b所示,(a)圆柱的截断( b)圆球的截断图5-7 投影为非圆曲线的截交线画法【典范例题】【例题一】补全棱柱截断体的三视图,见图5-8(a):(a)(b)(c)图5-8 棱柱的截交线画法剖析:1.求平面体的截交线的艰苦就是判别它是几边形.我们可以应用下面的办法进行判别,截平面与几条棱线订交就有几个极点(包括顶面和底面地点的边),与几个棱面订交就有几条边(包括顶面和底面),多个截平面截断时,截平面与截平面的订交处假如不与棱线重合,必然又多出了两个极点,即多了一条边.2.本形体用了P.Q两个截平面截断五棱柱,P平面为侧平面,Q平面为正垂面.Q平面与四个棱面,三条棱线订交,就必然有四条边三个极点(Ⅰ.Ⅱ.Ⅵ),平面Q与平面P订交就有一条边两个极点(Ⅲ.Ⅳ),所以可以剖断该截交线是一个五边形;应用同样的办法可判别出截平面P地点的截交线是一个四边形,如图5-8(b)所示.3.棱柱表面上的点都具有积累性,可以应用积累性求点法求截交线.截平面Q的正面投影都具有积累性,可在正面投影上取点1'.2'.3'.4'.5',其程度投影都积累在五边形的各条边上,可得程度投影1.2.3.4.5,依据正面投影和程度投影可求出侧面投影1".2".3".4".5",将1".2".3".4".5"按次序依次衔接就得到了截交线的侧面投影;平面P可应用同样的办法求出.形体前端被切去一块,将被切去的轮廓线擦失落,描深全图.如图5-8(c)所示.4.截交线的剖析办法有多种,可以依据具体情形采用最轻便的办法剖析.精确答案:如图5-8(c)所示.【例题二】补全棱锥截断体的其余投影,见图5-9(a):(a) (b) (c)图5-9 棱柱截交线的画法剖析:1.棱锥表面上求点的办法重要用积累性求点法和帮助线法.2.本形体是正三棱锥被P.Q两个截平面切去一块,Q面为平行于三棱锥底面的程度面, Q平面截一棱线得Ⅰ点,在主视图的投影为1',应用积累性求点法求出其程度投影1和侧面投影1",两截面P.Q的交线与三棱锥棱面的交点为Ⅱ点和Ⅴ点,应用帮助平面法和积累性求点法分离求出两点的程度投影2.5,侧面投影2".5",依次衔接Ⅰ.Ⅱ.Ⅴ各点同面投影即得截交线,如图5-9(b)所示.3.P平面为垂直于正面的正垂面,P平面截两棱线得Ⅲ.Ⅳ两点,在正面上的投影分离为3'.4',在棱线的其他两条棱线上求出另两面投影3.4和3".4"再分离衔接Ⅱ.Ⅲ.Ⅳ.Ⅴ各点的同面投影即得另一截交线,如图5-9(b)所示.4.正三棱锥被P.Q两截面切割失落了一部分,将切去部分的轮廓线擦去.最后描深全图,如图5-9(c)所示.精确答案:如图5-9(c)所示.【例题三】依据圆柱截断体的主视图和俯视图,画出其左视图,如图5-10(a)所示.(a)(b)(c)图5-10 圆筒截交线的画法剖析:1.求反转展转体截交线的难点是判别多个截平面切割时断定截交线的外形,这就得精确的判别截平面与反转展转体轴线的相对地位,然后再判别截交线的外形,还要弄清截平面订交处的分界线情形.最后按办法.步骤求出截交线的三面投影.2.本形体是一个圆柱沿着中间轴线挖一通孔后,形成了一个有内圆柱表面的圆筒,从主视图和俯视图(截断地位最显著的特点视图)可以看出,圆筒的上端又分离用一个程度面和一个侧平面各切去一块,下端用一个程度面和两个侧平面切去一块,形成一个凹槽,这就在内.外圆柱面上都产生了截交线.3.圆筒上端的两个程度面与圆柱的轴线平行,可判别其截交线是矩形,因为内.外圆柱面上都形成了截交线,所以前后各形成了两个矩形.四个矩形正面投影和程度投影都积累为竖线,侧面投影是反应实形的矩形,可应用积累性求点法,按投影纪律分离求出其三面投影.两个正平面与圆柱的轴线垂直,可判别其截交线是圆,因为是不完全截断,其截交线是由两段曲线和两段直线构成的圆平面,该平面在正面和侧面上都积累为横线,程度投影反应实形,也可应用积累性求点法分离求出其三面投影.下端的截断情形也可应用这种办法进行剖析,得出其截交线的投影,如图5-10(b)所示.4.求反转展转体的截交线还要精确剖析截平面是否将反转展转体的转向轮廓素线切去了,如图5-10(b)所示,圆筒的内.外圆柱面的左.右轮廓素线切去了,所以其主视图的转向轮廓线不完全(上端),其内.外转向轮廓素线都没有了;其前.后轮廓线切去了,所以其左视图轮廓线不完全,其内.外转向轮廓线也没有了,这种情形作图时要卖力剖析,必定要将被切去的转向轮廓素线擦去,最后描深全图,如图5-10(c)所示.精确答案:如图5-10(c)所示.【例题四】依据主视图和左视图,剖析共轴反转展转体的截断情形,补画出左视图,如图5-11(a)所示.(a)(b)(c)图5-11 同轴反转展转体的截交线画法剖析:1.本形体是由共轴的圆锥和圆柱构成,其轴线垂直于侧面.它的左上端被一个程度面P和一个正垂面Q切去一部分,在它的表面上共消失三条截交线和一条P平面和Q平面的交线.因为截平面P平行于轴线,所以它与圆锥面的截交线为双曲线,与圆柱面的截交线为矩形.因为截平面Q与圆柱轴线竖直订交,所以它与圆柱面的截交线为一段椭圆曲线.截平面P和圆柱面都垂直于侧面,所以三条截交线在侧面上的投影分离积累在截平面P和圆柱面的投影上,它们的正面投影分离积累在P.Q两平面的的正面投影上,是以只需求作三条截交线的程度投影.2.因为截交线共有三条,是以作图时应先求出相邻两条截交线的联合点,图中Ⅰ.Ⅴ两点在圆锥面和圆柱面的分界线上,是双曲线和矩形中一条线的联合点.Ⅵ.Ⅹ两点是矩形中两素线与椭圆曲线的联合点,位于P.Q两截平面的交线上.Ⅲ点是双曲线上的极点,它位于圆锥面最上面的轮廓素线上.Ⅷ点是椭圆曲线上的最右点,它位于圆柱面最上面的轮廓素线上.上述各点都是特别地位点.可应用积累性求点法求出Ⅰ.Ⅲ.Ⅴ.Ⅵ.Ⅷ.Ⅹ各点的另两面投影(1";3".5".6".8".10";1.3.5.6.8.10).1-12-10,5-11-6分离是直线,这就是平面P截切圆柱所形成的截交线.3.应用帮助平面法,求一般地位点Ⅱ.Ⅳ(2".4";2.4);应用在侧面上具有积累性求一般地位点Ⅶ.Ⅸ(7".9";7.9).4.在俯视图中,把1.2.3.4.5依次衔接即得双曲线的程度投影;把6.7.8.9.10依次衔接得椭圆的程度投影;因为被P.Q两个截面所截切,其交线为两个关闭的线框.除了求截交线外,还要留意截平面P截切圆柱和圆锥所形成的截交线的分界线,即画成虚线.精确答案:如图5-11(b)所示.【例题五】补全圆球截断体的三视图,如图5-12(a)所示.(a)(b)(c)图5-12 开槽圆球截交线的画法剖析:1.该圆球顶端由三个截平面开一通槽,槽的阁下两截面P为侧平面,与球面订交,截交线圆的侧面投影反应圆的实形;槽底为程度面,也与球面订交,截交线圆的程度投影反应实形.2.圆球被截平面截切时,截交线的外形都是圆.当截平面平行于根本投影面截切时,截交线在三视图中的投影,分离为直线和圆,截交线圆的直径的大小与截平面的地位有关,截平面距离球心愈近,直径愈大,反之愈小.所以在画截平面圆时,直径要精确的量取,P平面截得的圆的直径应当是R2,Q平面截得的圆的直径应当是R1,作图时必定要留意.如图5-12(b).(c)所示.求圆球截交线的办法主如果用帮助平面法,有积累性的点可以用积累性求点法.3.当圆球被两个或两个以上的截平面截切时,三视图中画出的截交线圆是不完全的,它画出的规模的大小是由瘦语的外形和大小决议的,当截平面把圆球的前后轮廓素圆截去时,影响到主视图的轮廓素圆不完全;当圆球的阁下轮廓素圆截去时,就影响到左视图素圆不完全;当圆球的高低轮廓素圆截去时,就影响到俯视图轮廓素圆不完全.画图时要精确性的剖析.如图5-12(b).(c)所示.精确答案:见图5-12(c)所示.【才能练习】一、断定题:1、截交线是平面与立体表面的交线,是平面与立体表面的共有线. ()2、因为截平面与圆柱轴线相对地位的不同,其截交线重要有圆.矩形和椭圆三种外形.()3、截平面与圆锥的轴线竖直截切时,其截交线的外形是双曲线. ()4、任何地位的截平面截切圆球时的截交线都是圆. ()5、截交线都是关闭的平面图形. ()二、依据投影关系,选择精确的视图:1.()2.3.()4.()5.()三.补画视图中的缺线:1. 2.3. 4.5. 6.四.补画所缺视图,求其表面上A.B.C三点的另两面投影,并在立体表面上连点成线,完成线ABC的三面投影.(保留作图帮助线)1. 2.3. 4.五.已知两视图,补画第三视图:1. 2.3. 4.5. 6.答案:一.1.( √ );2.( √ );3.( ×);4.( √ );5.( √ ).二.1.(3);2.(3);3.(3);4(1);5(1).三. 1. 2. 3.4. 5. 6.四. 1. 2.3. 4.五.1. 2. 3.4. 5. 6.二、相贯线的特点及画法:【考纲领求】1、控制应用积累性法求相贯线的办法;2、控制异径两圆柱正交时相贯线的近似画法;3、懂得相贯线的特别情形及其画法.【要点精讲】(一)相贯线的界说:两个立体订交所形成的交线称为相贯线.(二)相贯线的特点:1、相贯线是两个立体表面的共有线(共有点的聚集),也是两个立体表面的分界线;2、相贯线一般是关闭的空间曲线,特别情形下为平面曲线或直线.(三)求相贯线的办法:①积累性求点法;②帮助平面法.(四)相贯线的类型及画法:1.平面体与平面体相贯:相贯线的外形是平面直线(由直线构成的关闭的平面多边形),这种相贯线可转化为平面与根本体的截交线,是叠加式组合体中的相接这种表面接触方法.如图5-13所示,两个平面体的分界线都是由直线构成的平面多边形,只要按截交线的画法画出其分界线就可以了,不过还要剖析两个形体是否平齐照样不平齐,在这里就不再具体评论辩论了.图5-13 平面体相接图5-14 平面体与反转展转体相接图5-15 平面体与圆柱相贯2.平面体与反转展转体相贯:这种相贯可分为两种情形.(1)相贯线是平面直线:如图5-14所示两个形体的分界线是平面直线,这种情形同平面体与平面体相贯一样,也是叠加式组合体中的相接表面接触方法.(2)相贯线是由直线和曲线配合构成的空间图形:这种情形可以转化为求截平面截断反转展转体的截交线,常见的是平面体与圆柱垂直相贯.如图5-15所示,其相贯线是阁下对称的两段圆曲线和前后对称的两条直线段所构成的空间图形,两段圆曲线的正面投影和程度投影都积累为两段竖线,侧面投影阁下重合且反应实形,与圆柱的积累性圆的一部分重合.这有一种特别情形,也就是叠加式组合体中的相切,如图5-16(a).(b)所示,因为两形体相切,在相切处是滑腻过渡的,二者之间没有分界线.(a)(b)图5-16 平面体与圆柱相切3、反转展转体和反转展转体相贯:(1)相贯线的外形:一般情形是关闭的空间曲线,特别情形是平面曲线或直线.(2)求相贯线的本质:求两根本体表面的共有点,将这些点滑腻的衔接起来,即得截交线.(3)求相贯线的办法:①积累性求点法:重要指圆柱与另一反转展转体垂直相贯时的情形.当圆柱与另一反转展转体相贯时,假如圆柱轴线垂直于某一投影面时,就可以应用圆柱面投影的积累性得到相贯线的一面投影,再依据已知投影,应用投影常识求得相贯线的其他投影.这种情形应用积累性求点法就可以求出相贯线.②帮助平面法:帮助平面法的道理是在恰当地位选一个帮助平面,依次截切两个相贯的反转展转体,在每个反转展转体上得到两条截交线,截交线与两个反转展转体表面的素线的交点就是帮助平面与两个物体的共有点,即相贯线上的点.同理,如许截切数次,可得到一系列的共有点,再把这些点的投影依次滑腻的衔接起来,即得截交线的投影.从用帮助平面法求相贯线的道理来说,帮助平面可所以随意率性地位的.但为了作图便利,选择的帮助平面最好是投影面平行面,使帮助平面与反转展转体表面的截交线为圆或直线,也就是使截交线的投影为最简略的图形(圆或直线).(4)相贯线的作图步骤:①判别相贯的两个反转展转体的外形特点.②剖析两反转展转体的表面性质,想象相贯线的空间外形.③求相贯上的特别地位点(如最高.最低.最前.最后.最左.最右点)的投影.④应用积累性求点法或帮助平面法再求一系列的一般地位点(最好是对称点)的投影.⑤判别相贯线的对称性,肯定其投影是否重合,并判别相贯线的可见性,肯定相贯线的虚与实.⑥将求得的各点滑腻衔接,即得相贯线的投影.(5)圆柱与圆柱垂直订交(正交)时的相贯线的画法:a.两不等径圆柱垂直相贯时相贯线的画法:如图5-17(a).(b)所示.1)积累性求点法或帮助平面法:因为两圆柱的轴线分离垂直于侧面和程度面,其相贯线既在大圆柱表面上,也在小圆柱表面上,是两个圆柱表面的共有线,(a)(b)图5-17 积累性求点法和帮助平面法求不等径圆柱正交的相贯线所以,相贯线的程度投影与小圆柱的程度投影重合为一圆,相贯线的侧面投影为一圆弧,且在大圆柱的侧面投影的大圆周上,并界于小圆柱两转向轮廓素线之间的一段圆孤上.所以只需求出相贯线的正面投影.两圆柱正交时,其相贯线前后对称,阁下对称.其前.后.左.右都有特别点,这些特别点决议了相贯线的地位界线,相贯线的下面投影前半部分和后半部分重合为一段曲线.其求作步骤是:先应用积累性求点法求特别地位点,即最高点Ⅰ.Ⅱ(也是最左.最右点)和最低点Ⅲ;再用积累性求点法或帮助平面法求一般地位点Ⅳ.Ⅴ.Ⅵ点;最后将各点滑腻衔接即可.2)近似画法:在现实画图进程中,为了画图便利,对常见的的相贯线可采用近似画法,即在两圆柱轴线垂直订交,直径不等的情形下,如对作图精确度不作特别请求时,可简化作图,用圆弧代替这段非圆曲线,其作图办法如图5-18所示,即:以大圆的半径为半径,在小圆柱的轴线上找圆心,以这点为圆心,仍以大圆柱的半径为半径,在两圆柱转向轮廓线的交点之间向着大圆柱的轴线曲折画弧.b.两等径圆柱相贯:其相贯线是过两轴线交点的两订交直线,如图5-19所示.图5-18 不等径圆柱相贯线的简化画法图 5-19 等径圆柱正交的相贯线c.圆柱孔相贯:当圆柱上开圆柱孔或圆柱孔与圆柱孔在内部相贯时,它们的相贯线的画法,根本上与两圆柱相贯线的画法雷同,但要留意判别相贯线的可见性,如图5-20(a).(b).(c)所示.(a)圆柱上穿孔(b)两圆柱孔相贯(c)两等径圆柱孔相贯图5-20 圆柱上穿孔的相贯线(6)相贯线的特别情形及画法:两反转展转体相贯其相贯线一般为空间曲线.但在特别情形下,也可能是平面曲线或直线,下面分离简略介绍.a.当两个反转展转体具有公共轴线时,其相贯线为一平面圆,该圆的正面投影和侧面投影积累为一向线段,程度投影为反应实形的圆,如图5-21所示.(a)(b)(c)(d)图5-21 共轴反转展转体相贯b.当两等径圆柱相贯.圆柱与圆锥.圆锥与圆球.圆锥与圆锥轴线相贯,并公切于一圆球时,相贯线为椭圆,该椭圆的正面投影为一段直线,程度投影为相似形(圆或椭圆),如图5 -22所示.(a) (b) (c) (d)图5-22 轴线订交并公切于一圆球时的相贯c.两圆柱轴线平行相贯或两圆锥共锥顶相贯时,它们的相贯线为两条直线,如图5-23所示.(a)(b)图5-23 两轴线平等圆柱体相贯.两共锥顶圆锥相贯d.过渡线及画法:因为工艺和强度等方面的请求,在零件某些表面的订交处,往往用小圆角过渡,如许就使本来的相贯线不显著,为了差别平同的表面以便于识图,在本来的相贯处用过渡线画出,如图5-24所示,其画法与相贯线雷同,仅在轮廓线交点处断开,其两头与轮廓线不订交.当然,平面体与平面体相贯或平面体与曲面体相贯时也有过渡线,可自行剖析.图5-24 两圆柱垂直相贯的过渡线【典范例题】【例题一】依据两面视图,想出相贯线的外形,补画第三视图,如图5-25(a)所示.(a)(b)图5-25 平面体与曲面体相贯剖析:1.平面立体与曲面立体相贯可以转化为求平面与形体的截交线.2.程度圆筒与竖立的空心四棱柱体垂直相贯,在内.外圆柱面上各有一条相贯线.每条相贯线都由四棱柱体的四个棱面与圆柱产生的四条截交线所构成.3.外表面相贯线由两条是平行侧面的圆弧截交线M1.M2及两条是侧垂线的截交线N1. N2构成;其投影为m1.n1.m2.n2,m'1.n'1.m'2.n'2.m'2.n'2,m"1.n"1.m"2.n"2.4、内表面相贯线的构成与外表面相贯线雷同,未用文字注明.。


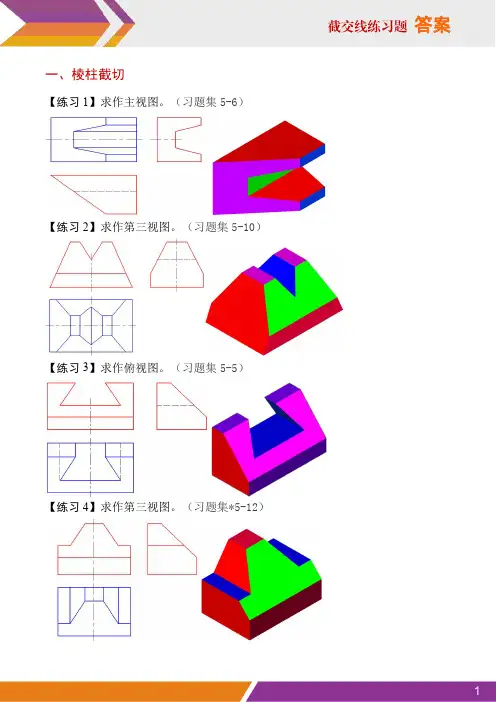
一、棱柱截切【练习1】求作主视图。
(习题集5-6)【练习2】求作第三视图。
(习题集5-10)【练习3】求作俯视图。
(习题集5-5)【练习4】求作第三视图。
(习题集*5-12)【练习5】求作第三视图。
(习题集*5-13)【练习6】求作第三视图。
(习题集*5-14)【练习7】求作左视图。
(习题集*5-15)【练习8】求作俯视图。
(习题集*5-16)【练习9】求作俯视图。
(习题集*5-17)【练习10】求作俯视图。
(习题集*5-18)【练习11】求作左视图。
(习题集*5-19)【练习12】求作左视图。
(习题集*5-20)【练习13】求作第三视图。
(习题集*5-21)【练习14】求作第三视图。
(习题集*5-22)【练习15】求作俯视图。
(习题集*5-23)【练习16】完成六棱柱截切后的水平投影,并求其侧面投影。
【练习17】根据立体的两面投影,求其侧面投影。
【练习18】求作俯视图。
【练习20】根据给出的视图,补画第三视图或视图中所缺的图线。
【练习21】根据给出的视图,补画第三视图(或视图所缺的图线)。
二、棱锥截切【练习1】完成三棱锥截切后的水平投影,并求其侧面投影。
【练习2】完成三棱锥截切后的水平投影,并求其侧面投影。
【练习3】求棱锥被截切后的投影。
【练习4】求棱锥被截切后的投影。
【练习5】完成三棱锥截切后的投影。
【练习6】完成三棱锥截切后的投影。
补充:三、圆柱截切【练习1】求作俯视图。
(习题集5-24)(1)(2)【练习2】求作俯视图。
(1)(习题集5-25)(2)【练习2(3)】求圆柱截切后的第三视图。
【练习2(4)】求圆柱截切后的第三视图。
【练习3】求作左视图。
【练习4】求作左视图。
(习题集5-26)【练习5】求作左视图。
(习题集5-27)【练习6】求作俯视图。
【练习7】求作左视图。
【练习8】求作俯视图。
(习题集5-30)【练习9】求作左视图。
(习题集5-31)【练习10】求作左视图。
(习题集5-32)【练习11(1)】求作左视图。


案例008与答案
案例:相贯线的特殊情况有哪些?
答案:两曲面体的相贯线,在一般情况下为封闭的空间曲线。
在特殊情况下,相贯线可能是直线,也可能是平面曲线。
一、相贯线为直线
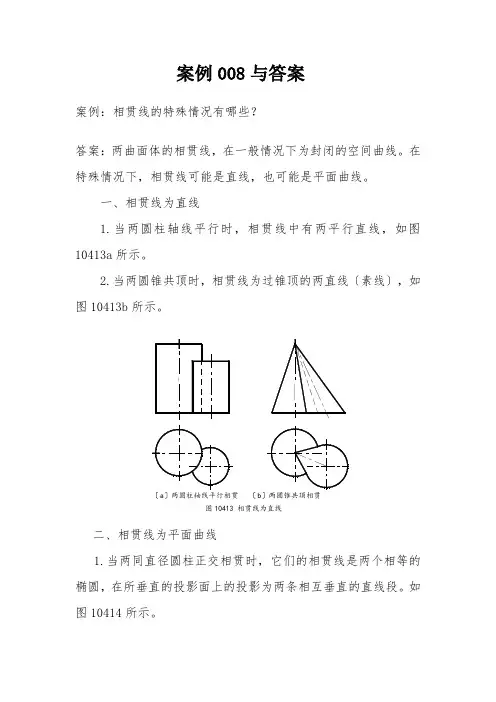
1.当两圆柱轴线平行时,相贯线中有两平行直线,如图10413a 所示。
2.当两圆锥共顶时,相贯线为过锥顶的两直线〔素线〕,如图10413b 所示。
二、相贯线为平面曲线
1.当两同直径圆柱正交相贯时,它们的相贯线是两个相等的椭圆,在所垂直的投影面上的投影为两条相互垂直的直线段。
如图10414所示。
〔a 〕两圆柱轴线平行相贯 〔b 〕两圆锥共顶相贯
图10413 相贯线为直线
2.当两回转体共轴线时,其相贯线是垂直于回转体轴线的圆;当轴线垂直于某投影面时,相贯线在该投影面上的投影为圆,且反映实形,另外两个投影面上的投影积聚为垂直于轴线的直线段。
如图10415所示。
图10414 同直径圆柱正交相贯图10415 回转体共轴线相贯。