第3节 立体与立体相交
➢3.1 概述
——求相贯线
➢3.2 直线与曲面立体相交
➢3.3 平面立体与平面立体相交
➢3.4 平面立体与曲面立体相交
➢3.5 曲面立体与曲面立体相交
➢3.6 复合相贯线
3.1 概述
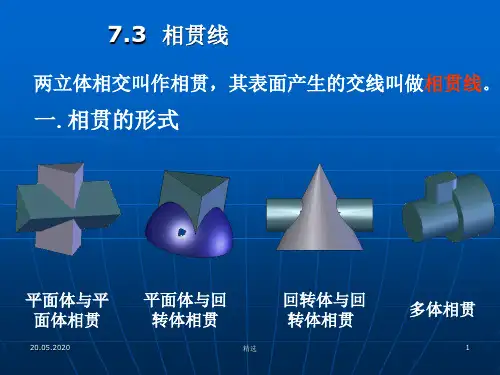
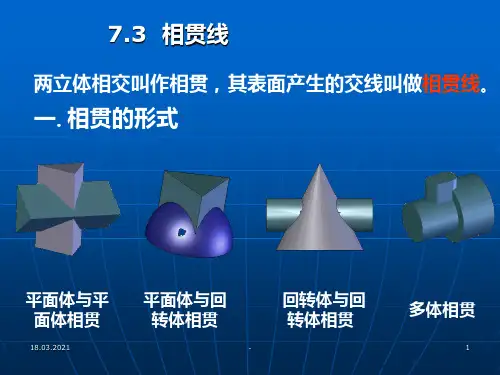
两立体表面相交时,它们表面的交线称为相贯线。
立体与立体相交可分为三种情况:
(1) 两平面立体相交。 (2) 平面立体与曲面立体相交。 (3) 两曲面立体相交。
特殊点
1. 利用积聚性的表面取点法
[例10] 求二圆柱的相贯线 分析:
面立体表面的共有点。
• 不同的立体以及不同的相贯位置,相贯线的形状也不同。
一般情况下两回转体相贯,相贯线为封闭的空间曲线,特殊 情况为平面曲线或直线。
3.5.1 两回转体相交
相贯线为二立体表面公共线
相贯线Βιβλιοθήκη 相贯线1.两回转体相交,交线为相贯线 2.相贯线为二立体表面的公共线 3.相贯线一般为封闭的空间曲线
3.3 平面立体与平面立体相交
平面立体与平面立体相贯时,由于平面立体是 由平面组成的,因此两平面立体的相贯线由折线组 成。折线的每一段都是A形体的一个侧面与B形体的 一个侧面的交线,折线的转折点就是一个形体的侧 棱与另一形体的侧面的交点。
相贯线实质就是平面与平面立体的截交线,整 个相贯线是由封闭的若干段平面截交线组成的。
2.求出相贯线上的特殊点Ⅰ、 Ⅱ 、Ⅲ、Ⅳ、Ⅴ 、Ⅵ、Ⅶ ;
3.求出若干个一般点Ⅷ、Ⅸ;
4.光滑且顺次地连接各点,作 出相贯线,并且判别可见性;
5.整理轮廓线。
2 PH
7 5
9 3
QH SH TH
[例9] 平面立体与曲面立体相贯,完成相贯线的投影