第一节 概
第二节
述
两回转体表面的相贯线
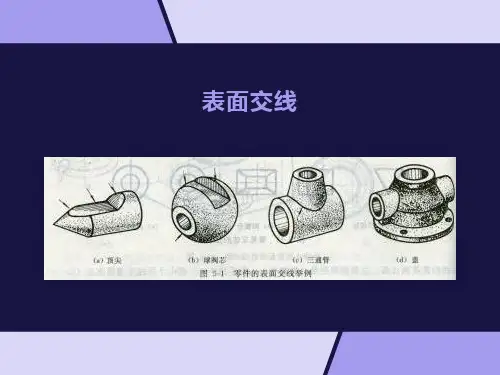
相贯: 相贯:两立体相交称为相贯 相贯体: 相贯体:参与相贯的立体叫做相贯体 相贯线: 相贯线:相交两回转体表面的交线叫做相贯线
相贯体
相贯线
相贯线的性质
共有性— 1)共有性 —相贯线是两相交回转体表面的共有线和分 界线,线上所有点都是两相交回转体表面的共有点。 界线 , 线上所有点都是两相交回转体表面的共有点。 是求相贯线投影的作图依据。 是求相贯线投影的作图依据。 封闭性—由于立体的表面是封闭的 由于立体的表面是封闭的, 2)封闭性 由于立体的表面是封闭的 , 因此相贯线一 般是封闭的线框。 般是封闭的线框。 形状—相贯线的形状决定于回转体的形状 相贯线的形状决定于回转体的形状、 3)形状 相贯线的形状决定于回转体的形状 、 大小以 及两回转体之间的相对位置( 及两回转体之间的相对位置 ( 一般情况下相贯线是空 间曲线,特殊情况下为平面曲线或直线) 间曲线,特殊情况下为平面曲线或直线)。
一般情况下两回转体相交, 一般情况下两回转体相交,相贯线为封闭的空间曲 但特殊情况下,相贯线可能是平面曲线或直线。 线;但特殊情况下,相贯线可能是平面曲线或直线。 1 .两等径圆柱正交 两等径圆柱正交的相贯线是平面曲线,是两个椭圆。
2 . 同轴回转体相贯
同轴回转体相交就是两个以上的基本体具有同一根轴的回转 其相贯线是垂直于轴线的圆。 体,其相贯线是垂直于轴线的圆。交线圆在轴线垂直的投影面上的 投影反映实形, 投影反映实形,在轴线平行的投影面上的投影是过两相交立体投影 轮廓线交点的一直线段 。 球与圆锥同轴
已知正交相贯两圆柱的水平投影和侧面投影, 例1 已知正交相贯两圆柱的水平投影和侧面投影, 求正面投影。 求正面投影。