课外练习1_成比例线段-优质公开课-鲁教8下精品

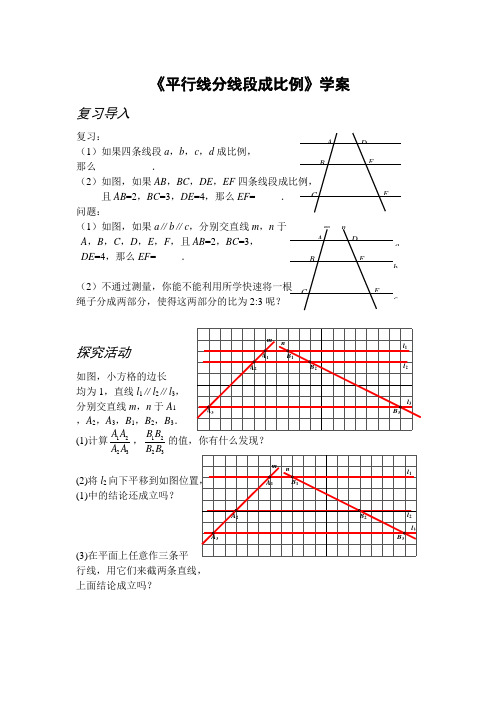
《平行线分线段成比例》学案复习导入复习： （1）如果四条线段a ，b ，c ，d 成比例，那么___________．（2）如图，如果AB ，BC ，DE ，EF 四条线段成比例，且AB =2，BC =3，DE =4，那么EF =_____．问题：（1）如图，如果a ∥b ∥c ，分别交直线m ，n 于A ，B ，C ，D ，E ，F ，且AB =2，BC =3， DE =4，那么EF =_____．（2）不通过测量，你能不能利用所学快速将一根 绳子分成两部分，使得这两部分的比为2:3呢？探究活动如图，小方格的边长 均为1，直线l 1∥l 2∥l 3， 分别交直线m ，n 于A 1 ，A 2，A 3，B 1，B 2，B 3．(1)计算1223A A A A ，1223B BB B 的值，你有什么发现？(2)将l 2向下平移到如图位置， (1)中的结论还成立吗？(3)在平面上任意作三条平 行线，用它们来截两条直线， 上面结论成立吗？A D C E BF A D C E B Fab cm n l 1l 2l 3m n B 3B 2B 1A 3A 2A 1l 1l 2l 3m n B 3B 2B 1A 3A 2A 1例 在△ABC 中，E ，F 分别是AB 和AC 上的点，且EF ∥BC ． （1）如果AE =7，EB =5，FC =4，那么AF 的长是多少？ （2）如果AB =10，AE =6，AF =5，那么FC 的长是多少？练习：1．已知直线l 1∥l 2∥l 3，DE =6，EF =7， AB =5，求AC 的长．2．在△ABC 中，D ，E ，F 分别是AB ，AC ，BC 上的点， 且DE ∥BC ，EF ∥AB ，AD :DB =2:3，BC =20， 求BF 的长．问题解决不通过测量，你能不能快速将一根绳子分成两部分，使得这两部分的比为2:3呢？能力提升1．如图所示，如果D ，E ，F 分别在OA ， OB ，OC 上，且DF ∥AC ，EF ∥BC ． 求证：OD ∶OA ＝OE ∶OB ．A DB F CEAD C EBFl 1 l 2l 3A B FCE ODCFBAE2．在△ABC中，DE∥BC，EF∥CD，AB=8，AF=2，求AD的长．作业布置一、必做题1．已知直线l1∥l2∥l3，BC=7，EF=4，AB=5，求AC的长．2．在△ABC中，D，E分别是AB和AC上的点，且ED∥BC ．（1）如果AD =3.2，DB=1.2，AE=2.4，那么EC的长是多少？（2）如果AB=5，AE=3，AF=4，那么EC的长是多少？二．选做题在△ABC中，D，E分别是AB和BC上的点，且ED∥AC，AB ACBE EC=，53ABAC=，求ABBD．FADCBEACDEBA DCEBFl1l2l3ADB CE。

1、 预习导学： 1、阅读课本，回答问题：（1）、两条线段的比就是 的比.比如：线段a 的长度为3厘米，线段b 的长度为6米，所以两线段a,b 的比为3∶6=1∶2,对吗？那么，应怎样定义两条线段的比，以及求比时应注意什么问题呢？ 如果选用 量得两条线段AB 、CD 的长度分别是m 、n ，那么就说这两条线段的比AB ∶CD= ，或写成CDAB = ，其中，线段AB 、CD 分别叫做这两个线段比的 和 . 如果把n m 表示成比值k ，则CD AB = 或AB= 归纳： ,叫做这两条线段的比。

注意：两条线段的长度必须 。

练习1.已知线段AB 和CD 的长度分别是2cm ，6cm ，则AB 和CD 的比是 ，表示为 . 练习2.已知在比例尺为1：500的大路中学规划图上侧得主教学楼到餐厅的距离是1.1cm ，则他们的实际距离为 m 2、做一做 如图，设小方格的边长为1，四边形ABCD 和四边形EFGH 的顶点都在格点上，那么AB 、AD 、EF 、EH 的长度分别是多少？分别计算EF AB、EH AD、AD AB 、EH EF的值,你发现了什么？ 对于四条线段a 、b 、c 、d ，如果d c b a =（或a ∶b ＝c ∶d ），那么，这四条线段叫做 ，简称比例线段，也称这四条线段成比例．（注意，a 、b 、c 、d 必须按顺序写出）。

特别的，若c b b a =，则称b 为a 、c 的比例中项。

3.比例的基本性质：（1）如果dc b a =，那么 ． （2）如果ad ＝bc （a 、b 、c 、d 都不等于0），那么 ． 4、例1：如图，一个矩形的长AB=am,宽AD=1m,按照图中所示的方式将它分割成相同的三个矩形，且使分割出的每个矩形的长与宽的比与原矩形的长与宽的比相同，即AB AD AD AE =，那么a 的值应当是多少？5、想一想：如果三个数a,b,c（a,b,c都不等于0）满足a2=ac,那么，a,b, b,c是否成比例6、练1．(1)已知M为线段AB上一点,AM=2cm，MB=4cm,求AM：BM；(2)已知M为线段AB上一点，AM：MB=3：5，且AB=16cm，求线段AM、BM的长度。

《成比例的线段》习题1．已知三条线的比如下，可以组成三角形的是( )A ．5：20：30B ．10：20：30C ．15：15：30D ．20：30：302．下列四条线段中，不能成比例的是( )A .a ＝3，b ＝6，c ＝2，d ＝4B ．a ＝1，b ＝2，c ＝6，d ＝3C .a ＝4，b ＝6，c ＝5，d ＝10D .a ＝2，b ＝5，c ＝15，d ＝233．在比例尺为1：n 的某市地图上，A ，B 两地相距5cm ，则A ，B 之间的实际距离为( ) A ．n 51cm B ．2251n cm C .5ncm D .252n cm 4．若5x =7y ，则y x 的值为( ) A ．75 B ．57 C ．3：5 D ．2 5．如果b a ＝b d 成立，那么下列各式一定成立的是( ) A ．c a ＝bd B ．bd ac ＝b c C ．b a 1+＝d c 1+ D ．b b a 2+＝dd c 2+ 6．若a :b :c =3:5:7，且3a +2b -4c =9，则a +b +c 的值等于( )A ．-3B ．-5C ．-7D ．-157．已知M 是线段AB 延长线上一点，且A M ：B M ＝5：2则AB ：BM 为( ) A .3：2 B ．2：3 C ．3：5 D ．5：28．某班同学要测量学校升国旗的旗杆高度，在同一时刻，量得某同学的身高是1.5米，影长是1米，且旗杆的影长为8米，则旗杆的高度是( )A .12米B ．11米C ．10米D ．9米9．若b b a -＝74，则ba ＝_________． 10．若b a ＝dc ＝52(b ＋d ≠0)，则db c a ++＝__________．11．已知5922=-+b a b a ，则b a ＝_______． 12．在△ABC 中，AB ＝12，点E 在AC 上，点D 在AB 上，若A E ＝6，E C ＝4，且EC AE DB AD =. (1)求AD 的长；(2)试问AC EC AB DB =能成立吗？请说明理由.。

第九章图形的相似1．成比例线段(一)一、学生知识状况分析相似图形是现实生活中广泛存在的现象，在小学时学生就接触过比例的知识，在七年级上册时学生已学习了全等图形（其实全等图形就是相似图形的一个特例）。

所以学生已经具备一些知识基础、活动经验基础等，学生在学习线段的比时不会感到很困难。

二、教学任务分析（一）教学知识点1、了解相似形、线段的比概念；2、会求两条线段的比, 应用线段的比解决实际问题。

（二）能力训练要求通过现实情境，进一步发展学生从数学的角度提出问题、分析问题和解决问题的能力，培养学生的数学应用意识，体会数学与自然、社会的密切联系。

（三）情感与价值观要求1．、．有关比例的计算，让学生懂得数学在现实生活中的作用，从而增强学生学好数学的信心；2．、．通过解答实际问题，激发学生学数学的兴趣，增长社会见识；3．、．在与他人的共同探索、讨论问题的过程中，增强合作交流的意识。

教学重点：理解线段比的概念及其求解。

教学难点：求线段的比，注意线段长度单位要统一。

教学方法：探索、发现法教学准备：多媒体课件三、教学过程分析本节课设计了六个教学环节：第一环节：设置情境，引入新课；第二环节：新课讲解；第三环节：随堂练习；第四环节：想一想；第五环节：回顾与思考；第六环节：布置作业。

第一环节 设置情境，引入新课活动内容：通过用幻灯片展示生活的的图片，引入本章的学习内容—相似图形。

活动目的：引发学生思考相似图形的特征，激发学生的学习兴趣。

实际效果：学生们都很兴奋，对学习充满了好奇心。

第二环节：新课讲解活动内容：1.请在下面图形中找出形状相同的图形？你发现这些形状相同的图形有什么不同？2. 引入线段的比:如果选用同一个长度单位量得两条线段AB,CD 的长度分别是m ，n ,那么就说这两条线段的比（ratio ）AB:CD =m:n ,或写成n m CD AB =其中,AB,CD 分别叫做这个线段比的前项和后项.如果把n m 表示成比值k,那么k CD AB =,或AB=k·CD.两条线段的比实际上就是两个数的比。

第九章图形的相似1．成比例线段教学目标：1．结合实际情境了解线段比的概念，并会计算两条线段的比．2．结合实际情境了解成比例线段的概念．3．理解并掌握比例的基本性质，并能进行简单应用．教学重点：理解线段的比和比例线段的概念，会求两条线段的比及判断线段是否成比例．教学难点：掌握比例的基本性质，并能进行简单应用．教学方法：探索、发现法教具学具：多媒体课件教学过程:一设置情境，引入新课活动内容：通过用幻灯片展示生活的的图片，引入本章的学习内容—相似图形。

活动目的：引发学生思考相似图形的特征，激发学生的学习兴趣。

实际效果：学生们都很兴奋，对学习充满了好奇心。

二讲授新课活动内容：1.请在下面图形中找出形状相同的图形？你发现这些形状相同的图形有什么不同？2. 引入线段的比:如果选用同一个长度单位量得两条线段AB,CD 的长度分别是m ，n ,那么就说这两条线段的比（ratio ）AB:CD =m:n ,或写成n m CD AB =其中,AB,CD 分别叫做这个线段比的前项和后项.如果把n m表示成比值k,那么k CD AB =,或AB=k ·CD.两条线段的比实际上就是两个数的比。

五边形 ABCDE 与五边形A ’B ’C ’D ’E ’形状相同，AB=5cm ，A ’B ’=3cm 。

AB: A ’B ’=5 : 3，就是线段AB 与线段A ‘B ’的比。

这个比值刻画了这两个五边形的大小关系。

3.想一想：两条线段长度的比与所采用的长度单位有没有关系？ 通过上面的活动学生应该对这个问题有了一定的认识:两条线段长度的比与所采用的长度单位无关.但要采用同一个长度单位.4.做一做：如图，设小方格的边长为1，四边形ABCD 与四边形EFGH 的顶点都在格点上，那么AB ，CD ，EH ，EF 的长度分别是多少？分别计算 值。

你发现了什么？ 四条线段a ，b ，c ，d 中，如果a 与b 的比等于c 与d 的比，即 = ，那么这四条线段a ，b ，c ，d 叫做成比例线段，简称比例线段.上图中AB,EH,AD,EF 是成比例线段，AB,AD,EH,EF 也是成比例线段。

第四章图形的相似．成比例线段（2）教学目标知识目标：了解线比例线段的基本性质；理解并掌握比例的基本性质及其简单应用；发展学生从数学的角度提出问题、分析问题和解决问题的能力。

能力目标：经历运用线段的比解决问题的过程，在观察、计算、讨论、想象等活动中获取知识。

情感与价值观目标：通过本节课的教学，培养学生的数学应用意识，体会数学与现实生活的密切联系。

教学重点：让学生理解并掌握比例的基本性质及其简单应用。

教学难点：运用比例的基本性质解决有关问题。

教学课时：第2课时教学过程：教学环节教学内容教师活动学生活动资源、运用设计意图第一环节回顾思考（1）成比例线段定义（2）比例的基本性质（3）若3m = 2n，你可以得到nm的值吗？mn呢？出示问题，引导学生分析并解决问题。

回忆相应知识点。

独立思考问题，然后请学生回答。

电子板展示学生思考回顾上节课的内容，更好的进入本节课的学习。

第二环节合作探究(1)如图，已知21==AECEADBD，你能求出AEAECEADADBD+=+的值吗？如果CEABBCAB=,那么CECEACBDBDAB-=-有怎么样的关系？在求解过程中，你有什么发现？已知，a，b，c，d，e，f六个数。

(2) 如图，HGADFGCDEFBCHEAB,,,的值相等吗？HGFGEFHEADCDBCAB++++++的值又是多少？在求解过程中，你有什么发现？已知，a，b，c，d，e，f六个数。

出示问题，引导学生思考。

1、合比性质有两种形式：如果dcba=，那么bba+＝ddc+；先独立思考5分钟，再小组交流2分钟，展示、评价和补充4分钟。

鼓励学生互相补充，畅所欲言，不要由老师替学生总结，特别要关注一些在数学学习中有困难的学生，要通过这个环节来给他们树立信心，同时帮助他们发现困难以便今后更好的解决困难。

电子板书写、展示每一个知识点的学习，都需要在一定的知识背景中去认识和练习才能得到巩固应用，从引例的结论中，引出“合比性质”及“等比性质”的学习。

鲁教版八年级下册数学第九章第1节 成比例线段（1）【学习目标】1.了解线段的比、比例线段的概念，会判断比例线段。

2.掌握比例的基本性质并能进行简单的运用。

【学习重点】成比例线段的概念和比例的基本性质【学习难点】判断比例线段，比例的基本性质的应用第一模块 自学设计自学任务一：自学教材84-85页内容，完成下列题目。

1、对于形状相同而大小不同的两个图形，我们可以用相应来描述他们的大小关系。

2、已知线段AB 和CD 的长度分别是2cm ，6cm ，则AB 和CD 的比是 ，表示为 .总结：两条线段的比：如果选用同一个长度单位量得两条线段AB,CD 的长度分别是m ，n,那么就说这两条线段的比AB:CD= 或写成 其中,AB,CD 分别叫做这个线段比的 和 .如果把n m表示成比值k,那么CD AB=K,或AB=两条线段的比实际就是 的比。

注意：两条线段的长度必须任务二：自学教材85页做一做，理解成比例线段。

1.归纳概念：在 条线段中，如果，那么这 条线段叫做成比例线段，简称比例线段。

2.填空：（1）四条线段a,b,c,d 中，如果a 与b 的比等于c 与d 的比，即 dc b a （或a:b=c:d ）那么这四条线段a,b,c,d 叫做 ，简称 .反过来，如果四条线段a,b,c,d 成比例线段，则可以记作 .（2）线段的比是指 线段之间的比的关系，而比例线段是指 线段间的关系.若两条线段的比 另两条线段的比，则这四条线段叫 .3.题型一：已知a=3,b=6,c=9(1)若a,b,c,x 是成比例线段，求x. (2)若a,x,b,c 是成比例线段，求x.4、题型二：已知a=1cm ，b=1.8cm ，c=3.5cm ，d=6.3cm ，这四条线段是成比例线段吗？总结方法步骤：先 再任务三：自学教材86页议一议，理解比例的基本性质。

1、比例的基本性质：如果dc b a ,那么 . 因为根据等式的基本性质，两边同时乘以 可得；反过来，同理可得，如果ad =bc （a ,b ,c ,d 都不等于0），那么 .还可以写成 形式。