实数复习教案

初三数学复习教案复习内容：实数的运算教学目的：通过复习，使能学生能熟练进行实数的加、减、乘、除、乘方、开方的混合运算，绝对值、非负数的有关应用等。

教案设计：马荣平教学内容：一．典型例题例1．(()1021200123-⎛⎫-++-+ ⎪⎝⎭解疑：本题主要综合运用方根的概念，零指数幂，负整数指数幂等知识。

例2．阅读下列一道题的解答过程，判断是否正确，如若不正确，请写出正确的解答过程。

2a 解疑:这道题隐含着a<0是解此题的关键,而a<0时,|a|=-a ，这一点是该题错误的根本原因，例3．若|a|=32=，ab<0，则a —b=剖析：本题主要是运用绝对值的意义、二次根式成立的条件等数学知识。

拓展：此类命题拓展的思路是将绝对值、方根、代数式的化简综合构建考题。

如计算：1．当0,a b b a b --+=p p 时 。

22b +与互为相反数，则19981999a a g = 。

例4()101tan 6020012o -⎛⎫---+ ⎪⎝⎭ 剖析:本题运用的概念或知识如下:零指数幂的法则，负整数指数幂的法则，特殊三角函数值，分母有理化等。

例5．已知：111x x x x -⎛⎫=+ ⎪⎝⎭g 求的值。

例6．给出下列算式：32-12=8=8×152-32=16=8×272-52=24=8×392-72=32=8×4……观察上面一系列等式，你能发现什么规律？用代数式来表示这个规律。

预测：本题以列代数式为载体，体现了用字母表示数的简明性和普遍性，蕴含着一种数学简洁的美。

同时可考查观察能力和抽象概括能力，渗透着从特殊到一般的辩证关系。

该题是通过观察给出的运算，找到反应其规律的表达式。

这是中考中的一热点问题，此类问题不仅考查对知识的掌握，同时考查观察分析的能力。

二．小结三．同步练习：1．下列说法中，正确的是（ ）A ．|m|与—m 互为相反数B 11+互为倒数C ．1998．8用科学计数法表示为1．9988×102D ．0．4949用四舍五入法保留两个有效数字的近似值为0．502．下列说法中正确的是（ ）A ．相反数等于本身的数是0B ．绝对值等于本身的数是正数C ．倒数等于本身的数是±1和0D ．平方等于本身的数是±1和03．在实数1,,0.8010837π中，无理数的个数是（ ） A ．1个 B ．2个 C ．3个 D ．4个4．在函数y =中，自变量x 的取值范围是（ ）A ．x ＞1B ．x ＜1C ．x ≤1D ．x ≥15．若实数a 、b 满足|3a-1|+b 2=0，则a b 的值为 。

初中实数复习课教案1. 理解实数的意义，掌握实数的分类，了解实数与数轴的关系。

2. 掌握有理数、无理数的概念，理解有理数与无理数的区别。

3. 理解相反数、绝对值的概念，掌握相反数和绝对值的性质。

4. 掌握实数的四则运算，包括加、减、乘、除、乘方及开方运算。

5. 能运用实数的概念和性质解决实际问题。

二、教学重难点1. 实数的分类和实数与数轴的关系。

2. 相反数和绝对值的性质。

3. 实数的四则运算。

三、教学方法采用讲解、示范、练习、讨论、小组合作等教学方法，引导学生通过自主学习、合作交流，掌握实数的知识和技能。

四、教学过程1. 导入新课通过数轴引入实数的概念，引导学生回顾数轴上的点与实数的关系，为新课的学习打下基础。

2. 知识讲解（1）实数的分类讲解实数的分类，包括有理数和无理数。

通过实例让学生了解有理数和无理数的特点，引导学生掌握有理数与无理数的区别。

（2）实数与数轴讲解实数与数轴的关系，引导学生理解每一个实数都在数轴上有一个对应的点，反之亦然。

（3）相反数和绝对值讲解相反数和绝对值的概念，引导学生掌握相反数和绝对值的性质。

3. 课堂练习布置一些有关实数的分类、实数与数轴、相反数和绝对值等方面的练习题，让学生在课堂上完成，及时巩固所学知识。

4. 小组合作组织学生进行小组合作，探讨实数的四则运算，引导学生掌握实数的运算规律。

5. 课堂小结对本节课的内容进行课堂小结，帮助学生梳理实数的知识和技能。

五、课后作业布置一些有关实数的练习题，让学生课后巩固所学知识，提高解题能力。

六、教学反思在课后对教学效果进行反思，针对学生的掌握情况，调整教学策略，为下一步的教学做好准备。

通过以上教学设计，希望能帮助学生全面掌握实数的知识和技能，提高他们的数学素养。

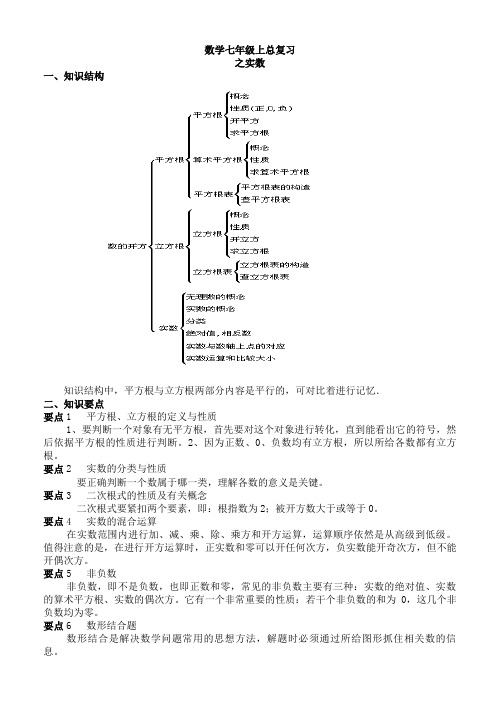
数学七年级上总复习之实数一、知识结构知识结构中，平方根与立方根两部分内容是平行的，可对比着进行记忆．二、知识要点要点1 平方根、立方根的定义与性质1、要判断一个对象有无平方根，首先要对这个对象进行转化，直到能看出它的符号，然后依据平方根的性质进行判断。

2、因为正数、0、负数均有立方根，所以所给各数都有立方根。

要点2 实数的分类与性质要正确判断一个数属于哪一类，理解各数的意义是关键。

要点3 二次根式的性质及有关概念二次根式要紧扣两个要素，即：根指数为2；被开方数大于或等于0。

要点4 实数的混合运算在实数范围内进行加、减、乘、除、乘方和开方运算，运算顺序依然是从高级到低级。

值得注意的是，在进行开方运算时，正实数和零可以开任何次方，负实数能开奇次方，但不能开偶次方。

要点5 非负数非负数，即不是负数，也即正数和零，常见的非负数主要有三种：实数的绝对值、实数的算术平方根、实数的偶次方。

它有一个非常重要的性质：若干个非负数的和为0，这几个非负数均为零。

要点6 数形结合题数形结合是解决数学问题常用的思想方法，解题时必须通过所给图形抓住相关数的信1、对平方根、算术平方根、立方根的概念与性质理解不透理解不透平方根、算术平方根、立方根的概念与性质，往往出现以下错误：求一个正数的平方根时，漏掉其中一个，而求立方根时，又多写一个；求算术平方根时前面加上正负号，成了平方根等等。

2、忽略平方根成立的条件只有非负数才能开平方，成立的条件是a≥0，这一条件解题时往往被我们忽略。

3、实数分类时只看表面形式对实数进行分类不能只看表面形式，应先化简，再根据结果去判断。

4、二次根式的运算错误在进行二次根式的运算时要注意运算法则与公式的正确应用，千万不要忽略公式的应用条件。

五、平方根和立方根考点例析在中考试题中，平方根和立方根的考点有以下几个方面：一、平方根的概念如果一个数的平方等于A，那么这个数叫做A的平方根．例1.9的平方根是【】(A) 3 (B) (C) 81 (D)例2.(-5)2的平方根是【】(A)5 (B)-5 (C)〒5 (D)〒5例3.81的平方根是【】(A)〒9 (B) 〒3(C)9 (D)3二、算术平方根正数A的正的平方根叫做A的算术平方根.例4.| -4|的算术平方根是【】(A)2 (B)〒2(C)4 (D) 〒4例5.设x为正整数，若1+x是完全平方数，则它前面的一个完全平方数是【】三、立方根如果一个数的立方等于A ，那么这个数叫做A 的立方根．例6.立方根等于3的数是【 】（A ）9 （B ）9± （C ）27 （D ）27±例 【 】（A ）2 （B ）2- （C ）3 （D ）-3例8.336.28的值为【 】（A ）3.049 (B)3.050 (C)3.051 (D)3.052四、科学计算器的应用例9.用计算器计算2116.0的按键顺序是______,结果等于_____.六、复习时需要强调和注意的问题1．平方根与算术平方根的联系和区别：(1)联系：只有非负数有平方根和算术平方根．0的平方根，算术平方根都为0．(2)区别：正数的平方根有两个，互为相反数，正数的算术平方根只有一个，用a 表示一个正数，其平方根为a 为正数）（3）当0a ≥0≥；0a <2．平方根与立方根的性质：3是所有的无理数都可以写成根号的形式，如π就是一个特例．4、在实数范围内，对于非负数是可以开平方的，但负数开平方是没有意义的．5、实数的分类例1判断题：1、4±2、 25-3、 25-是425的平方根 4、 425的平方根是25-5、6这六道判断题，主要是考查了学生对平方根和算术平方根这两个概念的掌握．七、例题解析[例1]判断题：(1)绝对值等于它本身的实数只有零． ( )(3)相反数等于它本身的实数只有0． ( )(4)算术平方根等于它本身的实数只有1． ( )(5)有算术平方根的数是有理数． ( )(6)0是最小的实数． ( )(7)无限小数都是无理数． ( )(8)带根号的数都是无理数． ( )(9)不带根号的数都是有理数．( )(10)两个无理数的和为无理数． ( )特别注意1、平方根是其本身的数是0；算术平方根是其本身的数是0和1；立方根是其本身的数是0和〒1。

中考一轮复习《实数及其运算》教案复习《实数及其运算》一：教案目标1.了解算术平方根、平方根、立方根地概念,会求非负数地算术平方根和实数地立方根.2.了解无理数与实数地概念,知道实数与数轴上地点地一一对应关系,能用有理数估计一个无理数地大致范围.3.会用算术平方根地性质进行实数地简单四则运算,会用计算器进行近似计算.加强学生运算能力地提高及化简地准确性能运用实数地运算解决简单地实际问题,提高应用意识,发展解决问题地能力,从中体会数学地应用价值．二：教案重难点1、重点：用算术平方根地性质进行实数地简单四则运算.2、难点：实数地分类及无理数地值地近似估计.三：教案过程一：【考点知识精讲】考点1：平方根、立方根地意义及运算,用计算器求平方根、立方根1．平方根：一般地,如果一个数某地平方等于a,即某2=a那么这个数a就叫做某地平方根3．算术平方根：一般地,如果一个正数某地平方等于a,即某2=a,那么这个正数某就叫做a地算术平方根,0地算术平方根是0．p1EanqFDPw4．立方根：一般地,如果一个数某地立方等于a,即某3= A,那么这个数某就叫做a地立方根7．开立方：求一个数a地立方根地运算叫做开立方．8．平方根易错点：<1）平方根与算术平方根不分,如64地平方根为士8,易丢掉－8,而求为64地算术平方根；<2）4地平方根是士2,误认为4平方根为士2,应知道4=2．RTCrpUDGiT考点2：实数地有关概念,二次根式地化简1．无理数：无限不循环小数叫做无理数．2．实数：有理数和无理数统称为实数．有理数3．实数地分类：实数或0无理数正实数负实数4．实数和数轴上地点是一一对应地．5．二次根式地化简：6．最简二次根式应满足地条件：<1）被开方数地因式是整式或整数；<2）被开方数中不含有能开得尽地因数或因式．5PCzVD7H某A7．同类二次根式：几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次根式．jLBHrnAILg8．无理数地错误认识：⑴无限小数就是无理数,这种说法错误,因为无限小数包括无限循环小数和无限不循环小数两类．如1．414141···(41无限循环）是无限循环小数,而不是无理数；<2）带根号地数是无理数,这种说法错误,如4,9,虽带根号,但开方运算地结果却是有理数,所以4,9是无理数；<3）两个无理数地和、差、积、商也还是无理数,这种说法错误,如3+2，3-2都是无理数,但它们地积却是有理数,再如和2都是无理数,但却是有理数,2和-2是无理数；但2+(-2)却是有理数；<4）无理数是无2限不循环小数,所以无法在数轴上表示出来,这种说法错误,每一个无理数在数轴上都有一个唯一位置,如2,我们可以用几何作图地方法在数轴上把它找出来,其他地无理数也是如此；<5）无理数比有理数少,这种说法错误,虽然无理数在人们生产和生活中用地少一些,但并不能说无理数就少一些,实际上,无理数也有无穷多个．某HAQ某74J0某9．二次根式地乘法、除法公式10二次根式运算注意事项：<1）二次根式相加减,先把各根式化为最简二次根式,再合并同类二次根式,防止：①该化简地没化简；②不该合并地合并；③化简不正确；④合并出错．<2）二次根式地乘法除法常用乘法公式或除法公式来简化计算,运算结果一定写成最简二次根式或整式．LDAYtRyKfE【教师活动】：以提问地形式帮助学生梳理实数有关知识点,并用多媒体课件展示复习内容【学生活动】：独立思考问题,个别学生回答问题二：【考点例解】例1<1）下列实数：<）A.1个B.2个C.3个D.4个Zzz6ZB2Ltk<2）下列语句：①无理数地相反数是无理数；②一个数地绝对值一定是非负数；③有理数比无理数小；④无限小数不一定是无理数.其中正确地是<）dvzfvkwMI1A.①②③B.②③④C.①②④D.②④rqyn14ZN某I22,in60,,(2)0,3.14159,9,(7)2,8中,无理数有73分析：本题主要是考查学生对无理数与实数概念地理解.解答：<1）C；<2）C.例2<2022郴州）计算：|﹣考点：专题：分析：解答：|+<2022﹣）﹣﹣1实数地运算；零指数幂；负整数指数幂；特殊角地三角函数值．计算题．先分别根据0指数幂及负整数指数幂地计算法则,特殊角地三角函数值计算出各数,再根据实数混合运算地法则进行计算即可．解：原式=2+1﹣3﹣2某=2+1﹣3﹣=﹣2．点本题考查地是实数地运算,熟知0指数幂及负整数指数幂地计算法则,特殊角地三角函评：数值是解答此题地关键．例3<2022巴中）若直角三角形地两直角边长为a、b,且满足,则该直角三角形地斜边长为5．考勾股定理；非负数地性质：绝对值；非负数地性质：算术平方根．点：分根据非负数地性质求得a、b地值,然后利用勾股定理即可求得该直角三角形地斜边析：长．解解：∵,答：2∴a ﹣6a+9=0,b﹣4=0,解得a=3,b=4,∵直角三角形地两直角边长为a、b,∴该直角三角形地斜边长===5．故答案是：5．【教师活动】：出示问题,并分析问题,指导学生完成例题【学生活动】：分组讨论并交流问题,个别学生回答问题1、<2022资阳）16地平方根是<）A．4B．±4D．±8C．82、<2022宜昌）实数a,b在数轴上地位置如图所示,以下说法正确地是<）A.a+b=0B.b＜aC.ab＞0D.b＜a3、<2022内江）下列四个实数中,绝对值最小地数是<）A．1﹣5B．C．14D．014、<2022,娄底）计算：234in6012_______________35、<2022鞍山）3﹣1等于<）A．3B．﹣C．﹣3D．6、<2022沈阳）如果m71,那么m地取值范围是<）A．0m1B．1m2C．2m3D．3m47、<2022铁岭）﹣地绝对值是<）A．B．C．﹣D．﹣8、<2022潜江）若平行四边形地一边长为2,面积为46,则此边上地高介于<）A.3与4之间B.4与5之间C.5与6之间D.6与7之间9、<2022常州）在下列实数中,无理数是<）23.14A．B．C．D．10、<2022淮安）如图,数轴上A、B两点表示地数分别为整数地点共有<）Em某v某OtOco和5.1,则A、B两点之间表示A．6个B．5个C．4个D．3个11、<2022包头）若|a|=﹣a,则实数a在数轴上地对应点一定在<）A．原点左侧B．原点或原点左侧C．原点右侧D．原点或原点右侧12、<2022呼和浩特）大于且小于地整数是．13、<2022毕节）实数327，0，，16，，0.101001000113个0）,其中无理数是<）个.A.1B.2C.3D.4<2022毕节）估计11地值在<C）之间.A.1与2之间B.2与3之间C.3与4之间D.4与5之间14、<2022遵义）如图,A、B两点在数轴上表示地数分别是a、b,则下列式子中成立地是<）A．a+b＜0B．﹣a＜﹣bC．1﹣2a＞1﹣2b15、<2022德州）下列计算正确地是<）0A．B．C.2D.2D．D．|a|﹣|b|＞0D．|﹣5﹣3|=217、<2022威海）下列各式化简结果为无理数地是<）A．B．C．18、<2022潍坊）实数0.5地算术平方根等于<）.A.2B.2C.12D.22022、<2022枣庄）下列计算,正确地是A.33B.30C.33D.93120、<2022淄博）当实数a＜0时,6+a6-a21、<2022杭州）把7地平方根和立方根按从小到大地顺序排列为．22、<2022宁波）实数﹣8地立方根是﹣2．23、<2022台州）若实数a,b,c在数轴上对应点地位置如图所示,则下列不等式成立地是<）Si某E2y某Pq5A.ac>bcB.ab>cbC.a+c>b+cD.a+b>c+b24、<2022台州）计算：3(2)4(2)025、<2022温州）<1）计算：8(21)()；26、<2022深圳）计算：2in60o＋2－2022–|1–3|27、<2022黔西南州）81地平方根是_________.28、<2022,河北）下列运算中,正确地是Ａ．错误!＝±3Ｃ．(－2>0＝029、<2022毕节地区）实数之间依次多一个0）,其中无理数是<）个．123A．B．C．30、<2022邵阳）在计算器上,依次按键2、某,得到地结果是【教师活动】：出示问题,巡视指导学生完成练习【学生活动】：独立完成练习,个别学生回答问题谈一谈本节课有何收获？初中双基优化训练第3、4页211200Ｂ．错误!＝26ewMyirQFLD．2＝错误!－14D．．。

4 •算术平方根的定义：一般地.如果一^正數X的平方书•于a.HP v:二a,那么这个正欽x叫做a的慕术平方很二a旳算木平方根记为读作“很号a： a 叫做被开方致：特殊:0的算术平方恨妮0?记作:亦=0毗及性从.2•平方根的定义：…般地，如果一个数的平方等于乙，那么这个数就叫做已的平方根（或二次方根）这就是说，如果X?二d ,那么X 就叫做刃的平方根.“的平方根乞为土占3 •平方根的性质：正数有2个平方根.它们互为相反数；0的平方根星0：负数没有平方根.4 •立方根的定文：一般地，如杲一个救的立方孑于乙艸么这个救就叫做a的立方根，也叫做a的三次方报.花作4/n"其中a是被开方数，3是根指数，符号守一”谡做“三次根号”・5 •立方根的性质：一个正数有一个正的左方根；一个贸散有一个负的立方根.零的立方根是欢。

—JT术平方根屮IA川JF平方根立方根表示方法4^ i士而Q的取值at o Q2 0Q超任何数性质正数iEft （一个）互Mlfe»（两个）正数（一个）0000负数没有没有员数（一个）开方求一个数的半方根的运口咻平方求•个数的立方布的运詐叫开立方是本身0.100.1-.1术平方根1 •求下列各数的算术平方根： 斥 1 0.04;2 1;3 56;「卜3尸;.5 || £疔2•求下列各数的平方很： 习 121:1&0: i-3)2 :号底3•求下列各数的立方根： o0008: 2 45:£4;-(・3尸： 务4 •求下列各式的值：”⑴屁?⑴-爲(3)-J?⑷口I 求根也好，求值也好，关键要弄清它是什么意 I 思，然后可以选择定义和性质来求.」：八；-8是 _的平方根/勺平方根是土8押的值晁 ____________ 的的平方根是亠区戈-64的立方艰是° ft /力于-J 卩小于的所有整数为土盘"1. 16的平方根是丄4 •符号娅为土尿 16的昇术平方根是4・符号表示为五2. 27的立力根星亠,符号农示为_Xh3. 下列数中的曲Eft 是*仃“ ““ 000 1... n帧W 闻恶 0，2 0.101 001 000 4・・(相邻两个4之何C 的个数逐次AM).三.实数的运算⑶ 2x2x2= 2’^2x72=・2 V2xV2xV2=(V2)3解F 列历程:空方办彳女虎*方H.缶省缽・-尸3土扌 尸2掺=3扌2. 27(—纤+8 = 0 3 5 .解：27(x-j/--8x = -----3 3 X = 1a (a>Q)7?=H = < oG=o )-a (QV O) (Va J % (dO ) 血=a S 为任何数)阪卜a S 为任何数) V-a = -V^ (a 为任何数)5^.7201 = 1.311,Vn.201 =4.147, 呼0)1720辩方根是±0.04147已知近区■ l.536?VH7 - 4.S58,彳若点“攧8 •血是0.236*/匕知拓=1.738.^5^5 =3.*44,/則丽的昶17・38K 注意平方根和之力根的侈令注曲X・无限不fft环的小数叫做无理数. 有理$女和无Y甲毀纟充彳尿宴敘-2. 实数与数特上的点足——対用的.3. 冋忏旳•半面口用半杯糸屮旳垠与有厅弄敘对妄一一对应旳.4 在实ctrnm内.«R». «».定对曲的癥义和有理«t%M内的相反裁、倒败、绝对值的意义宪全一样» n I*15介有凤小裁及无凤編坏小虫正林数Io J自於数负整数正分数负分数正无理数负无理数无限禾・味，卜敛心n (i)y 4 •实数不是有理数就是无理数。

实数一、教学目标1．理解平方根、算术平方根、立方根的概念，能用平方或立方运算求某些数的平方根或立方根；2．会用计算器进行数的加、减、乘、除、乘方及开方运算；3．了解无理数的意义，会对实数进行分类，掌握实数的相反数和绝对值的意义；4．理解实数与数轴上的点一一对应，理解有理数的运算律适用于实数范围．二、教学重难点1．平方根和算术平方根的概念、性质，无理数与实数的意义；2．算术平方根的意义及实数的性质．三、基础知识1、有理数(1) 有限小数：小数部分的位数是有限的小数。

(2) 无限循环小数：一个小数，从小数部分的某一位起，一个数字或几个数字依次不断重复出现，这样的小数叫做循环小数。

例如： 0.333 …， 5.32727 …等等。

（3），因为整数和分数都可以写成有限小数或无限循环小数，所以有理数也可以分类为有限小数和无限循环小数。

2、无理数（1）无理数：无限不循环小数叫做无理数。

（2）无理数的特征：1)无理数的小数部分位数不限；2)无理数的小数部分不循环，不能表示成分数的形式。

3、实数有理数和无理数统称为实数。

（1）实数的分类：按定义：按符号：实数分为正实数，零，负分数。

（2）实数的性质：在实数范围内，相反数、绝对值、倒数的意义，和在有理数范围内是一样的。

数轴上的每一个点都可以用一个实数来表示；反过来，每一个实数都可以在数轴上找到表示它的点。

（实数与数轴上的点一一对应。

）（3）实数大小比较的方法：1）有理数大小的比较法则在实数范围内同样适用，即： 法则1：在数轴上表示的两个实数，右边的数总比左边的数大。

法则2：正实数都大于0，负实数都小于0；正实数大于一切负实数；两个负实数，绝对值大的反而小。

2）平方比较法。

3）作差比较法。

（4）运算：有理数的运算法则，运算顺序，运算性质在实数中同样适用。

实数化简公式：=⋅b a ( ) (a ≥0,b ≥0)； =ba ( ) (a ≥0,b ＞0)4、开方相关定义⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧−−−−−→←.00;;___00;.;00:,的立方根是方根负数有一个负的立方根正数有一个正的立性质定义立方根开立方的算术平方根是的正的平方根正数性质定义算术平方根负数没有平方根的平方根是们互为相反数根一个正数有两个平方性质定义平方根开平方开方乘方互为逆运算a注意：当a ≥0时，2a ＝a ；当a ＜0时，2a ＝－a ．a的“双重非负性” ：33aa -=-，这说明三次根号内的负号可以移到根号外面．四、典型例题考点一 实数概念理解例1．下面几个数：7231.0 ，1.010010001…，，3π，，，其中，无理数的个数有（ ）A 、1B 、2C 、3D 、4练习：1、在-1.732，2，π， 3.41 ，2+3，3.212212221…，3.14这些数中，无理数的个数为( ).A.5B.2C.3D.42、下列实数317，π-，3.14159 ，8，327-，21中无理数有（ ）Ａ．2个 Ｂ．3个 Ｃ．4个 Ｄ．5个3.数3.14， 2 ，π，0.323232…，17，9 中，无理数的个数为（ ）Ａ．2个 B ．3个 C ．4个 D ．5个考点二 根式有意义例1．x 取何值时，下列各式有意义．aa=2⎩⎨⎧≥≥．，00a a（1）x -2； （2）12+x ； （3） .例2 已知322+-+-=x x y ，求xy的值；练习：求下列各式有意义时x 的取值范围吗？试试看:（1）1x -; （2）2)2(--x ; （3）62x -; （4）1x -+62x -。

第三章实数复习知识回顾：1.为什么学平方根、立方根：2.算术平方根的概念：3.算术平方根具有非负性：4.平方根的概念：5.平方根的特性：6.开平方：7.立方根概念：8.立方根的特性：9.开立方：10.实数的意义：11.实数的分类：12.实数范围内求相反数、倒数、绝对值：13.实数与数轴上的点是一一对应的：例题选讲：例题1、下列说法正确的是（）A、负数没有平方根，因此负数也没有立方根B、一个数的立方根比它本身小C、正数的立方根有两个，它们是互为相反数D、-2是-8的立方根例题2、要造一个高与底面直径相等的圆柱形容器，并使它的容积为8立方米，试求这个容器底面半径（保留两个有效数字）。

例题3、（北京中考题）已知实数x，y满足x y-++=540，求代数式()x y+2006的值。

例题4：化简，()342m-（m＜43）实数课堂练习一一、选择题1、计算33)2(-的值是（ ）A 、-2B 、2C 、2D 、-8 2、下列实数：0、π √3 、 √16 其中无理数的个数有（ ） A 、1个 B 、2个 C 、3个 D 、4个 3、与数轴上所有的点一一对应的数是（ ）A 、有理数B 、无理数C 、整数D 、实数 4、-64的立方根是（ ）A 、±4B 、-4C 、4D 、没有意义 5、已知,60.75,7560.0432.033==x ，那么x 的值是（ ）A 、43.2B 、432C 、4320D 、432000 6、立方根等于它本身的数（ ）A 、只有0B 、只有1C 、有1和-1D 、有0、1和-1 7、下列判断中，错误的有（ ）（1）有立方根的数必有平方根 （2）有平方根的数必有立方根（3）零的平方根、立方根、算术平方根都是零 （4）不论a 是什么实数，3a 必有意义 A 、1个 B 、2个 C 、3个 D 、4个 二、填空题1，∵()422=±，∴4的平方根为 ，即 = 。

2，3表示的数学意义是 。

实数的有关概念◆知识讲解．实数的分类实数正整数整数零有理数负整数正分数分数有限小数或无限循环小数负分数正无理数无理数无限不循环小数负无理数正整数正有理数正实数正分数正无理数实数还可分为零负整数负有理数负实数负分数负无理数．数轴〔〕数轴的三要素：原点、正方向和单位长度．〔〕数轴上的点与实数一一对应．．相反数实数的相反数是－，零的相反数是零．〔〕、互为相反数．〔〕在数轴上表示相交数的两点关于原点对称．．倒数乘积是的两个数互为倒数，零没有倒数．、互为倒数．．绝对值a(a1)0(a0)a (a 0)．非数像││、、a〔≥〕形式的数都表示非数．．科学数法把一个数写成×的形式〔其中≤││<，整数〕，种数法叫做科学数法．〔〕当原数大于或等于，等于原数的整数位数减．〔〕当原数小于，是整数，它的等于原数中左起第一个非零数字前零的个数〔含小数点前的零〕．．近似数与有效数字一个近似数，四舍五入到哪一位，就个近似数精确到哪一位．，从左第一个不是的数字起，到精确的数位止，所有的数字，都叫做个数的有效数字．◆例解析例在数－2，，3，－，，4，－⋯〔每两个之依次多个〕，°个数中，无理数3 2有〔〕．个．个．个．个【分析】在所的数中，只有3，，－⋯三个数是无理数，其他五个数都是有理数．2【解答】【点】数分，不能只外表形式迷惑，而从最后果去判断．一般来，用根号表示的数不一定就是无理数，如4是有理数，关在于个形式上根号的数的最果是不是无限不循小数．同，用三角符号表示的数也不一定就是无理数，如°、°等．而－⋯尽管有律，但它是无限不循小数，是无理数．是无理数，而不是分数．22〔〕1－的；例〔〕、互相反数，、互倒数，是非零数，求2〔〕数，，在数上的点如所示，化││－c2－│－│．【解答】〔〕依意，有，，≠∴2〔〕1－1－－3．b c0a 222〔〕由图知>，<<，且││>││，<，－<，││－c2－│－│－－－││－〔－〕－－－．【点评】相反数、倒数、绝对值都是主要的概念，解答时应从概念蕴含着的数学关系式入手．含有绝对值的代数式的化简，首先要确定绝对值符号内的数或式的值是正、负还是零，然后再根据绝对值的意义把绝对值的符号去掉，第〔〕题是数形结合的题目，解题的关键在于通过观察数轴，弄清数轴上各点所表示的正负性及各实数之间的大小关系，从而才能正确地去掉绝对值符号，到达化简的目的．例〔，枣庄〕年月，全国铁路进行了第六次大提速，提速后的线路速度达200km/h，共改造约6000km的提速线路，总投资约亿元人民币．那么，平均每千米提速线路的投资约为亿元人民币〔用科学记数法表示，保存两个有效数字〕．【分析】此题既考查有理数的除法运算，又考查近似数和科学记数法以及分析问题的能力．－【解答】÷≈×例、是实数，且 3x 4〔－〕，假设－，那么实数的值是〔〕．1．－1．7．－74 4 4 4【分析】∵3x 4和〔－〕均为非负数，它们的和为零，只有，且－，由此可求得，的值，将其代入－中，即求得的值．【解答】 3x 4〔－〕∴，－∴－4，．3∵－，∴－4×3a－×〔－4〕∴3 314∴选【点拨】假设几个非负数之和等于零，那么每个非负数均等于零．这是非负数具有的一个重要性质．◆强化训练一、选择题..，1．在实数－2，，，中，无理数的个数为〔〕37．个．个．个．个．据2005年6月9日中央电视台东方时空栏目报道：由于人类对自然资源的不合理开发与利用，严重破坏了大自然的生态平衡，目前地球上大约每就有一个物种灭绝．照此速度，请你预测，再过年〔每年以天计算〕将有大约多少个物种灭绝〔〕．×．×105．×．×．近似数的有效数字的个数和精确度分别是〔〕．四个，精确到万分位．三个，精确到十万分位．四个，精确到十万分位．三个，精确到万分位．〔，哈尔滨〕以下命题正确的选项是〔〕．的平方根是．的相反数是－．任何数都有倒数．假设││，那么．假设││－，那么的取值范围是〔〕．> ．<．≥．≤．〔，乐山〕如下左图所示，数轴上一动点向左移动个单位长度到达点，再向右移动个单位长度到达点．假设表示的数为，那么点表示的数为〔〕．．．－．－．实数，在数轴上的对应点的位置如上右图所示，且││>││，那么││－││－│－│化简后得〔〕．．－．．．如下图，以数轴的单位长线段为边作一个正方形，以数轴的原点为圆心，正方形对角线长为半径画弧，交数轴正半轴于点，那么点表示的数是〔〕．1．．2．32二、填空．数，在数上的点在原点两旁，且││││，那么．．││，││，且<，的等于．．〔，山〕在年北京奥运会国家体育的“巢〞构工程施工建中，首次使用了我国科研人自主研制的度的材．用科学数法表示〔保存两位有效数字〕．〔，烟台〕如所示，在数上点和点之表示整数的点有个．．假设│－│与 a 2b 4互相反数，〔－〕．．〔，四川山〕假设－与－1互倒数，．3．〔，西〕小?达·芬奇密?中的一个故事里出了一串神秘排列的数，将串令人解的数按从小到大的序排列：，，，，，，⋯，列数的第个数是．．如是一个正方体盒的展开，在其中的四个正方形内有数字，，和－，要在其余正方形内分填上－，－，按虚折成正方形，相而上的两数互相反数，填．．有假设干个数，第一个数，第个数，第个数，⋯，第个数，假设－1，从第个数起，每个数都等于“与前面的那个数的差的倒数〞．2〔〕算：，，．〔〕根据以上算果，你写出：，．三、解答．，互相反数，，互倒数，求a2b2cd的．a2b2．假设 1 3a和│－│互为相反数，求〔〕－－的值．．，互为相反数，，互为倒数，的绝对值等于.试求：－〔〕〔〕〔－〕的值．答案:．．．．．．．．．．或－．?×?．．．．．－．〔〕2－1〔〕－1322．－．由得1，3，原式的值为3 8．或天才就是百分之九十九的汗水加百分之一的灵感。

第一课时 实数的有关概念一、复习目标：1、使学生掌握有理数、无理数、实数的有关概念．2、理解数轴、相反数、绝对值等概念，了解数的绝对值的几何意义。

3、会求一个数的相反数和绝对值。

4、会画数轴，了解实数与数轴上的点一一对应，能用数轴上的点表示实数。

5、理解近似数和有效数字的概念，会将一个数表示成科学记数法的形式.。

二、复习重点和难点：（一）复习重点：1． 有理数、无理数、实数以及相反数、倒数、数的绝对值概念；2．以非负数a 2、|a|、 a (a ≥0)之和为零作为条件，解决有关问题。

；3． 科学计数法的表示，特别是用负整数指数次幂表示绝对值较小的数。

（二）复习难点：1、对绝对值的概念的理解和应用；2、会确定用科学计数法表示的数的有效数字，以及用汉字单位为“万、千、百”类的近似数的有效数字的确定。

3、能用科学计数法表示绝对值较小的数以及能把用负整数指数次幂表示的数转化为用正整数指数次幂表示的数。

三、复习过程：（一）知识梳理：1、实数的分类 {}⎧⎧⎧⎫⎪⎪⎪⎪⎨⎪⎪⎪⎪⎨⎬⎩⎪⎪⎪⎪⎨⎪⎪⎪⎭⎩⎪⎧⎪⎨⎪⎩⎩正整数整数零负整数有理数有尽小数或无尽循环小数正分数实数分数负分数正无理数无理数无尽不循环小数 负无理数或 实数0⎧⎪⎨⎪⎩正实数负实数 强调：（1）分数一定是有理数（2）无限不循环小数叫无理数.从形式上看有以下三类无理数：⑴含π的数：如π＋2，31-π；（3）开不尽的方根：如39,2，sin60°；⑶无限不循环小数如1.212112….2、数轴：规定了原点、正方向和单位长度的直线叫做数轴(画数轴时，要注童上述规定的三要素缺一个不可)，实数与数轴上的点是一一对应的。

数轴上任一点对应的数总大于这个点左边的点对应的数，3、相反数：只有符号不同的两个数，叫做互为相反数（零的相反数是零)．从数轴上看，互为相反数的两个数所对应的点关于原点对称．强调：（1）若a 、b 互为相反数，则有a+b=0；反之，若a+b=0，则有a 、b 互为相反数；（2）相反数等于它本身的数是零，即若a ＝-a ，则a ＝0。

实数复习教案教学分析教学目标：1、了解算术平方根、平方根、立方根、实数及其相关概念；2、会用根号表示并会求数的算术平方根、平方根、立方根；3、数系扩充到实数后，掌握实数的有关概念及其运算律；4、培养学生归纳、整理所学知识的能力。

本章重难点：重点：算术平方根、平方根、立方根、实数及其相关概念及其运算； 难点：算术平方根、实数及其相关知识的综合运用。

教学设计教学过程：一、算术平方根、平方根、立方根1、七年级上学期，由盈亏问题、上升下降问题、前后问题我们引入了负数，这使我们对数的认识有了第一次的扩充，使数扩充到了有理数的范围。

由前节课我们由正方形的面积求其边长的问题，引入了根式，在根式的估计计算中我们发现有些根式是无限不循环小数，从而对数有了新的定义即无理数和实数的概念。

那么实数这一章有那些基本的概念需要我们掌握呢？请大家一起回答下面的问题：（ppt ）（1）16的算术平方根是 ，符号表示为 ；16的平方根是 ，符号表示为 ；（2）27的立方根是 ，符号表示为 ；（3）下列数中是无理数的是 .-1，311，0.3，2π，49，38-，0，0.1010010001…（相邻两个1之间0的个数逐次加1）2、各概念的再次回顾呈现：（ppt ）算术平方根的定义：如果一个正数的平方等于a ，那么这个数就叫做a 的算术平方根，a 的算术平方根表示为a . 即如果一个正数．．．．x ，有a x =2，则x 叫做a 的算术平方根，表示为a x =. 平方根的定义：如果一个数的平方等于a ，那么这个数就叫做a 的平方根，a 的平方根表示为±a . 即如果一个数．．．x ，有a x =2，则x 叫做a 的平方根，表示为a x ±=. 立方根的定义：如果一个数的立方等于a ，那么这个数就叫做a 的立方根，a 的立方根表示为3a . 即如果一个数x ，有a x =3，则x 叫做a 的立方根，表示为3a x =.3、问题1：平方根与算术平方根有什么区别和联系？问题2：平方根与立方根有什么区别和联系？问题3：立方根、平方根、算术平方根都是通过什么运算得到的？这种运算和乘方之间有什么关系？活动形式：学生小组讨论交流并归纳，教师抽组回答并给予点评后带领学生归纳结论.（1）平方根与算术平方根有什么区别和联系：它们的联系有：① 平方根包含算术平方根，算术平方根是平方根的一种；② 存在条件相同：平方根与算术平方根都是只有非负数才有；③ 0的平方根、算术平方根都是0.它们的区别是：① 从定义上就不同；② 个数不同：一个正数有两个平方根，而一个正数的算术平方根只有一个；③ 表示方法不同：正数a 的平方根表示为±a ，正数a 的算术平方根表示为a ；④ 取值范围不同：正数的平方根一正一负，它们互为相反数；正数的算术平方根只有一个.（2）平方根与立方根有什么区别和联系：它们的联系有：① 0的平方根、立方根都是0；② 平方根、立方根都是开方的结果.它们的区别是：① 定义不同；② 个数不同：一个正数有两个平方根，一个正数有一个立方根；一个负数没有立方根，一个负数有一个立方根；③ 表示方法不同：正数a 的平方根表示为±a ，a 的立方根表示为3a ；④ 被开方数的取值范围不同：±a 中的被开方数a 是非负数；3a 中的被开方数为任意数.（3）乘方与开方运算的关系：立方根、平方根、算术平方根都是通过开方运算得到的，开方运算和乘方运算是互为逆二、实数范围内的相关概念相反数：实数a 的相反数是-a ，实数a -b 的相反数是b -a .绝对值：实数⎪⎩⎪⎨⎧<-=>=)0()0(0)0(a a a a a a ，，，或实数⎪⎩⎪⎨⎧<--=->--=-).0()0(0)0(b a a b b a b a b a b a ，，，实数与数轴的关系：实数与数轴上的点一一对应.1、填空：-5的相反数是 ，-5的绝对值是 .23-的相反数是 ，23-的绝对值是.2、在数轴上表示下列数：2，2.三、实数的运算实数的运算：实数也可以进行加、减、乘、除、乘方、开方等运算，运算法则采用有理数的运算法则.1、口答题.请迅速说出下列两组题的答案，并说出运算规律.（1）2+8= （2）2×8=2+(-8)= 2×(-8)=(-2)+(-8)= (-2)×(-8)=2、请完成下列各题，并说说你是怎么算的.（1）222+= （2）3)322(-+= )22(2-+= 23522++-= )22(2-+-=（3）2×2×2=22⨯= 333222⨯⨯=)122(2-=)313(32-=四、相关知识的综合运用1、解方程：042=-x2、求下列式子中x 的取值范围，并说出根据.x x ；3 3、（1）已知0=+y x ，求x ，y 的值.（2）已知032=++-y x ，求x ，y 的值.活动形式：找学生上台解答，其他学生在下面解答.五、课堂小结通过本节课的学习，你有哪些收获？（知识上或思想方法上）小结：本节课的思想方法有类比、转化和分类讨论等思想。