高考文科数学训练题练习题：天天练 26

高二数学天天练（26） 姓名课题：两直线的位置关系（2）一、选择题：1.若直线1l 到直线2l 的角为1θ，2l 到1l 的角为2θ，则cos （1222θθ+）的值为（ ）不能确定2.直线1l 到直线2l 的角为α，tan α的值为 （ ）A.正数B.负数C.实数或不存在D.实数3.已知直线1l ：x-3y+7=0，2l ：x+2y+4=0，下列说法正确的是 （ ）A.1l 到2l 的角是34πB.1l 到2l 的角是4πC.2l 到1l 的角是34πD.1l 到2l 的夹角是34π4.两条直线x-y+6=0与x+y+6=0的夹角是 （ ） A.4π B. 34π C.0 D.2π5.直线2x+4y+9=0到直线3x+ay+24=0的角是34π。

则a 等于 （ ）A.-9B.1C.-3D.-16.直线x=2和直线的夹角是 （ ） A.3π B.6π C. 2π D.23π7.若直线1l ，2l 的斜率分别是62x +x-1=0的两根，则1l 与2l 的夹角是 （ ）A.15°B.30°C.45°D.60°8.直线3x+3y+8=0到直线xsin α+ycos α+1=0(4π＜α＜2π) 的角是 （ ）A.α-4πB. 4π-α C.α-34π D.54π-α二、填空题：9.两条直线y=x （x ≥0）和y=-x （x ≤0）的夹角是 .10.若直线y=3x+6与直线y=kx+1的夹角为45°，则k 的值为 .11.的夹角等于30°，则其方程是 . 三、解答题： 12.直线l 在y 轴上的截距是1，并且l 到直线2x+3y+6=0的角为6π，求直线l 的方程. 13.如图，已知△ABC 的一条内角平分线CD 的方程是2x+y-1=0，两个顶点A （1，2），B （-1，-1），求第三个顶点C 的坐标.14.如图，在y 轴上给定两点A （0，a ），B （0，b ）（a ＞b ＞0），试在x 轴的正半轴上（原ACB 取最大值. 15.已知正方形的中心为（1，4），一个顶点为A （0，2），求过A 的正方形的两边所在直线的方程.。

2020届全国高考数学压轴题天天练（二十六）★祝考试顺利★注意事项：1、考试范围：高考范围。

2、试题卷启封下发后，如果试题卷有缺页、漏印、重印、损坏或者个别字句印刷模糊不清等情况，应当立马报告监考老师，否则一切后果自负。

3、答题卡启封下发后，如果发现答题卡上出现字迹模糊、行列歪斜或缺印等现象，应当马上报告监考老师，否则一切后果自负。

4、答题前，请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置，并将准考证号条形码粘贴在答题卡上的指定位置。

用2B铅笔将答题卡上试卷类型A后的方框涂黑。

5、选择题的作答：每个小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。

6、填空题和解答题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。

如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

7、选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。

答案用0.5毫米黑色签字笔写在答题卡上对应的答题区域内，写在试题卷、草稿纸和答题卡上的非选修题答题区域的答案一律无效。

8、保持答题卡卡面清洁，不折叠，不破损，不得使用涂改液、胶带纸、修正带等。

9、考试结束后，请将本试题卷、答题卡、草稿纸一并依序排列上交。

【安徽省芜湖市2019届高三5月模拟（文)】如图，点为单位圆上一点，，点沿单位圆逆时针方向旋转角到点，则（）A．B．C．D．【答案】D【解析】∵点A为单位圆上一点，，点A沿单位圆逆时针方向旋转角α到点，∴A（cos，sin），即A（，），且cos（α），sin（α）．则sinα＝sin[（α）]＝sin（α）cos cos（α）sin，故选：D．【新疆乌鲁木齐地区2019届高三第三次质量检测文】高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，用其名字命名的“高斯函数”为:设，用表示不超过的最大整数，则称为高斯函数,例如: ,，已知函数,则函数的值域为( ) A．B．C．D．【答案】C【解析】的定义域为，，因为，所以，所以的值域为，所以的值域为，故选C.【安徽省芜湖市2019届高三5月模拟理)】已知函数，，若有4个零点，则的取值范围为（）A．B．C．D．【答案】B【解析】当x=0时，g(0)=f(0)-0=0，当时，由题意可得，即y=a与y有3个交点且交点的横坐标不为0，令h(x)=,则h′（x）=，则x=，且在（0，）单增，在（）上单减，∴y的大致图像如图：又h()=若y=a与y有3个交点且交点的横坐标不为0，则，故选B.【安徽省芜湖市2019届高三5月模拟（文)】已知椭圆，直线与椭圆相交于，两点，若椭圆上存在异于，两点的点使得，则离心率的取值范围为（）A．B．C．D．【答案】B【解析】设P(),直线y=x过原点，由椭圆的对称性设又两式做差，代入上式得,故所以故选：B【新疆乌鲁木齐地区2019届高三第三次质量检测文】已知抛物线的焦点为,直线过焦点与抛物线分别交于，两点，且直线不与轴垂直，线段的垂直平分线与轴交于点，则的面积为( )A．B．C．D．【答案】C【解析】设直线，，则由可以得到，所以的中点，线段的垂直平分线与轴交于点，故.所以的中垂线的方程为：，令可得，解方程得.此时，到的距离为，所以.故选C.【四川省乐山市高中2019届高三第三次调查研究文】如图，边长为的正方形中，点分别是的中点，将，，分别沿，，折起，使得、、三点重合于点，若四面体的四个顶点在同一个球面上，则该球的表面积为( )A．B．C．D．【答案】B【解析】由题意可知△是等腰直角三角形，且平面．三棱锥的底面扩展为边长为1的正方形，然后扩展为正四棱柱，三棱锥的外接球与正四棱柱的外接球是同一个球，正四棱柱的对角线的长度就是外接球的直径，直径为：．球的半径为，球的表面积为．故选：．【四川省内江市2019届高三第三次模拟理】已知函数是偶函数，则下列结论可能成立的是（）A．，B．，C．，D．，【答案】D【解析】根据题意，设，则，则由，又由函数是偶函数，则，变形可得，即，必有，分析可得，可得满足题意，故选D。

第64练 平面向量的坐标表示及运算（1）目标：掌握平面向量的坐标表示，能准确表述向量的加法、减法、实数与向量的积的坐标运算法则，并能进行简单的应用.一、填空题1．若a =（3, -1），b =（-1,2），则a +b =__________．【答案】（2,1）【解析】a +b =（2，1）．2.已知点A (3，4)，B (－2，1)，则−→AB ＝ .【答案】(－5，－3) .３．已知a ＋b ＝(１,３),a －b ＝(３,－３),则a ,b 的坐标分别是 .【答案】（2,0），（-1,3）4.在平面直角坐标系中，O 为坐标原点，有下列结论：①每个向量的坐标表示是唯一的；②向量AB 的坐标就是点B 的坐标；③点A 的坐标就是向量OA 的坐标；④若两个向量相等，则它们的坐标相同.其中不正确的是 （填序号）.【答案】②【解析】向量AB 的坐标就是点B 的坐标减去点A 的坐标，故②错误，其它结论易知正确.5.若向量(2,3)a x =- 与向量(1,2)b y =+ 相等，则x y += .【答案】4【解析】由题意，(2,3)(1,2)x y -=+，即21,32,x y -=⎧⎨=+⎩解得3,1,4x y x y ==+=. 6.已知点A （x ,2），B （5,y -2），若AB =（4，6），则x 、y 的值分别为 .【答案】x =1,y =10【解析】由点 A （x ,2），B （5,y -2），则(5,22)(5,4)AB x y x y =---=-- =（4，6），所以5-x =4且y -4=6，解得x =1, y =10．7.已知点A(2,3)、B(-4,5)，则与AB 共线的单位向量是_______.【答案】)1010,10103(-或)1010,10103(- 【解析】)2,6(-=，102||=，则与AB 共线的单位向量是)1010,10103(-=或)1010,10103(-=. 8.设向量(1,3),(2,4),a b =-=- 若表示向量4,32,a b a c - 的有向线段首尾相接能构成三角形，则向量c = .【答案】(4,6)-【解析】依题意，得4(32)0a b a c +-+= ，故23(2,6)(6,12)c a b =--=-+-(4,6)=-.9.已知向量(1,2)a →=，(2,3)b →=-，(4,1)c →=，若用→a 和→b 表示→c ，则→c = . 【答案】2a b -【解析】设c xa yb =+ ，则(,2)(2,3)(2,23)(4,1)x x y y x y x y +-=-+=，24,231,2,1x y x y x y -=+===-.10.已知1(1,2),(4,10)2a b a b -=+=- ,则a = . 【答案】(2,2)-【解析】由1(1,2)2a b -= 得，2(2,4)a b -= ①，(4,10)a b +=- ②， 由①②联立解得(2,2)a =- ．二、解答题11.在∆ABC 中，点P 在BC 上，且−→BP ＝2−→PC ，点Q 是AC 的中点，若−→P A ＝(4，3)，−→PQ ＝(1，5)，求−→BC 的坐标.解：∵−→QC ＝−→AQ ＝−→PQ －−→P A ＝(－3，2)，∴−→PC ＝−→PQ ＋−→QC ＝(－2，7)，∴−→BC ＝3−→PC ＝(－6，21) .12.已知点A (－2,4)、B (3，－1)、C (－3，－4)且CM →＝3CA →，CN →＝2CB →，求点M 、N 及MN →的坐标．解:∵A (－2,4)、B (3，－1)、C (－3，－4)，∴CA →＝(1,8)，CB →＝(6,3)，∴CM →＝3CA →＝(3,24)，CN →＝2CB →＝(12,6)．设点M (x ，y )，则有CM →＝(x ＋3，y ＋4)，∴⎩⎨⎧ x ＋3＝3，y ＋4＝24，∴⎩⎨⎧ x ＝0，y ＝20， ∴点M 的坐标为(0,20)．同理可求得N (9,2)，因此MN →＝(9，－18)，故所求点M 、N 的坐标分别为(0,20)、(9,2)，MN →的坐标为(9，－18)．。

高二数学天天练（26） 姓名课题：两直线的位置关系（2）一、选择题：1.若直线1l 到直线2l 的角为1θ，2l 到1l 的角为2θ，则cos （1222θθ+）的值为（ ）A.2B.1C.0D.不能确定2.直线1l 到直线2l 的角为α，tan α的值为 （ ）A.正数B.负数C.实数或不存在D.实数3.已知直线1l ：x-3y+7=0，2l ：x+2y+4=0，下列说法正确的是 （ ）A.1l 到2l 的角是34πB.1l 到2l 的角是4πC.2l 到1l 的角是34πD.1l 到2l 的夹角是34π4.两条直线x-y+6=0与x+y+6=0的夹角是 （ ） A.4π B. 34π C.0 D.2π5.直线2x+4y+9=0到直线3x+ay+24=0的角是34π。

则a 等于 （ ）A.-9B.1C.-3D.-16.直线x=2和直线x-3y+6=0的夹角是 （ ） A.3π B.6π C. 2π D.23π7.若直线1l ，2l 的斜率分别是62x +x-1=0的两根，则1l 与2l 的夹角是 （ ）A.15°B.30°C.45°D.60°8.直线3x+3y+8=0到直线xsin α+ycos α+1=0(4π＜α＜2π) 的角是 （ ）A.α-4πB. 4π-α C.α-34π D.54π-α二、填空题：9.两条直线y=x （x ≥0）和y=-x （x ≤0）的夹角是 .10.若直线y=3x+6与直线y=kx+1的夹角为45°，则k 的值为 .11.x-y+8=0的夹角等于30°，则其方程是 . 三、解答题： 12.直线l 在y 轴上的截距是1，并且l 到直线y+6=0的角为6π，求直线l 的方程. 13.如图，已知△ABC 的一条内角平分线CD 的方程是2x+y-1=0，两个顶点A （1，2），B （-1，-1），求第三个顶点C 的坐标.14.如图，在y 轴上给定两点A （0，a ），B （0，b ）（a ＞b ＞0），试在x 轴的正半轴上（原ACB 取最大值. 15.已知正方形的中心为（1，4），一个顶点为A （0，2），求过A 的正方形的两边所在直线的方程.。

2021年高考数学模拟训练卷 (26)一、单项选择题（本大题共12小题，共60.0分）1.已知集合A={x∈R|y=log2(1−x)}，集合B={y|y=2x,x∈A}，则(∁R A)∩B=()A. (−∞,2]B. [12,4) C. [2,+∞) D. [1,2)2.已知复数z=i(1−3i)1+i，则复数z−的虚部为()A. 1B. −1C. iD. −i3.若曲线|y|=x+2与C：x24λ+y24=1恰有两个不同交点，则实数λ取值范围为()A. (−∞,−1]∪(1，+∞)B. (−∞,−1]C. (1,+∞)D. [−1,0)∪(1,+∞)4.对于直线m，n和平面α，β，能得出α⊥β的一个条件是()A. m⊥n，m//α，n//βB. m⊥n，α∩β=m，n⊂αC. m//n，n⊥β，m⊂αD. m//n，m⊥α，n⊥β5.执行如图的程序框图，如果输入的x为3，那么输出的结果是()A. 8B. 6C. 1D. −16.已知数列{a n}是公差为3的等差数列，{b n}是公差为5的等差数列，若b n∈N∗，则数列{a bn}为()A. 公差为15的等差数列B. 公差为8的等差数列C. 公比为125的等比数列D. 公比为243的等比数列7.已知函数f(x)=x3+bx2+cx的图象如图所示，则x1⋅x2等于()A. 2B. 43C. 23D. 128. 设函数f(x)=asinxcosx −2sin 2x ，若直线x =π6是f(x)图象的一条对称轴，则( )A. f(x)的最小正周期为π，最大值为1B. f(x)的最小正周期为π，最大值为2C. f(x)的最小正周期为2π，最大值为1D. f(x)的最小正周期为2π，最大值为29. 已知双曲线x 212−y 24=1的右焦点为F ，若过点F 的直线与双曲线的右支有且只有一个交点，则此直线的斜率的取值范围是( )A. [−√33,√33]B. [−√3,√3]C. (−√33,√33)D. (−√3,√3)10. 党的十九大报告指出，建设教育强国是中华民族伟大复兴的基础工程，必须把教育事业放在优先位置，深化教育资源的均衡发展．现有4名男生和2名女生主动申请毕业后到两所偏远山区小学任教．将这6名毕业生全部进行安排，每所学校至少安排2名毕业生，则每所学校男女毕业至少安排一名的概率为( )A. 425B. 25C. 1425D. 4511. 已知函数f(x)={1−x,x ≤0log 2x,x >0，若关于x 的方程f(f(x))=m 有两个不同的实数根x 1，x 2，则x 1+x 2的取值范围为( )A. [2,3)B. (2,3)C. [2ln2,4)D. (2ln2,4)12. 如图，边长为2的正方形ABCD 中，P ，Q 分别是边BC ，CD 的中点，若AC ⃗⃗⃗⃗⃗ =x AP ⃗⃗⃗⃗⃗ +y BQ⃗⃗⃗⃗⃗⃗ ，则x =( ) A. 2 B. 83 C. 65 D. 1225二、填空题（本大题共4小题，共20.0分）13. 已知α∈(0,π2)，且cos(α+π4)=513，则sinα= ______ ．14. 由曲线y =sinx ，y =cosx 与直线x =0,x =π2围成区域的面积为______ ．15.已知a>0，(1+ax)4(x+2)的展开式中x2项的系数为1，则a的值为______．ax2+ax+1有两个极值，则实数a的取值范围为__________．16.已知函数f(x)=2e x+12三、解答题（本大题共7小题，共82.0分）17.已知数列{a n}的前n项和为S n，并且满足a1=2，na n+1=S n+n(n+1)(1)求数列{a n}的通项公式；(2)令T n=S n，当n≥3时，求证：T n>T n+1．2n18.如图，四棱锥P−ABCD中，PA⊥底面ABCD，△ACD是边长为2的等边三角形，且AB=√2，PA=2，点M是棱PC上的动点．(1)求证：平面PAC⊥平面PBD；(2)当线段MB最小时，求直线MB与平面PBD所成角的正弦值．19. 已知抛物线y 2=4√2x 的焦点为椭圆x 2a 2+y2b2=1(a >b >0)的右焦点，且椭圆的长轴长为4，M 、N 是椭圆上的动点 (1)求椭圆标准方程；(2)设动点P 满足：OP ⃗⃗⃗⃗⃗ =OM ⃗⃗⃗⃗⃗⃗⃗ +2ON ⃗⃗⃗⃗⃗⃗ ，直线OM 与ON 的斜率之积为−12，证明：存在定点F 1，F 2，使得|PF 1|+|PF 2|为定值，并求出F 1，F 2的坐标；(3)若M 在第一象限，且点M ，N 关于原点对称，MA 垂直于x 轴于点A ，连接NA 并延长交椭圆于点B ，记直线MN ，MB 的斜率分别为k MN ，k MB ，证明：k MN ⋅k MB +1=0．20. “全国文明城市”已成为一块在国内含金量最高、综合性最强、影响力最大的“金字招牌”.为提升城市管理水平和区域竞争力，提升市民素养和群众幸福指数，某市决定参与创建“全国文明城市”.为确保创建工作各项指标顺利完成，市“创建办”拟通过网络对市民进行一次“文明创建知识”问卷调查(一位市民只参加一次).通过随机抽样，得到参加调查的100人的得分统计如下表：组别频数112222525114(1)由频数分布表可以大致认为：此次问卷调查的得分，μ近似为这100人得分的均值．求得分在区间(80,94]的概率P(80<ξ≤94)；(注：同一组的数据用该组区间的中点值作代表)赠送话费的金额(元)3050概率(2)在(1)的条件下，市“创建办”为鼓励市民积极参与创建问卷调查，制定了如下奖励方案：①得分不低于μ的可以获赠2次随机话费，得分低于μ的可以获赠1次随机话费；②每次获赠的随机话费和对应的概率如右表所示：现有市民甲参加此次问卷调查，记X(单位：元)为该市民参加问卷调查获赠的话费，求X的分布列与数学期望．附：参考数据：①35×1+45×12+55×22+65×25+75×25+85×11+95×4=6600；②；③若，则，．21.已知函数f(x)=x−klnx，常数k>0．(1)若x=1是函数f(x)的一个极值点，求f(x)的单调区间；(2)若函数g(x)=xf(x)在区间(1,2)上是增函数，求k的取值范围．22.已知平面直角坐标系xOy，直线l过点P(0,√3)，且倾斜角为α，以O为极点，x轴的非负半轴为极轴建立极坐标系，圆C的极坐标方程为ρ2−4ρcos(θ−π3)−1=0．(1)求直线l的参数方程和圆C的标准方程；(2)设直线l与圆C交于M、N两点，若|PM|−|PN|=√2，求直线l的倾斜角的α值．23.已知函数f(x)=|2x−1|+|2x+a|，g(x)=x+3．(Ⅰ)当a=−2时，求不等式f(x)<g(x)的解集；(Ⅱ)设a>−1，且当x∈[−a2,12)时，f(x)≤g(x)，求a的取值范围．【答案与解析】1.答案：D解析：解：集合A={x∈R|y=log2(1−x)}={x|1−x>0}={x|x<1}，集合B={y|y=2x,x∈A}={y|0<y<2}，∴∁R A={x|x≥1}，∴(∁R A)∩B={x|1≤x<2}=[1,2)．故选：D．化简集合A、B，根据补集与交集的定义写出运算结果．本题考查了集合的定义与应用问题，是基础题．2.答案：A解析：解：由z=i(1−3i)1+i =3+i1+i=(3+i)(1−i)(1+i)(1−i)=2−i，得z−=2+i．则复数z−的虚部为1．故选：A．直接利用复数代数形式的乘除运算化简得答案．本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．3.答案：A解析：解：如图曲线|y|=x+2与C：x24λ+y24=1图形：当C：x24λ+y24=1为椭圆时，必须满足图形中的红线，此时λ>1，当C：x24λ+y24=1为双曲线时，y=±x为双曲线的渐近线，可得2√−λ≤1，可得λ≤−1．所以则实数λ取值范围为：(−∞,−1]∪(1，+∞)．故选：A．画出图形，判断C：x24λ+y24=1是椭圆或双曲线时，求解实数λ取值范围．本题考查椭圆与双曲线的综合应用，考查数形结合以及计算能力．4.答案：C解析：解：在A中，m⊥n，m//α，n//β，则α与β相交或相行，故A错误；在B中，m⊥n，α∩β=m，n⊂α，则α与β不一定垂直，故B错误；在C中，m//n，n⊥β，m⊂α，由由面面垂直的判定定理得α⊥β，故C正确；在D中，m//n，m⊥α，n⊥β，则由面面平行的判定定理得α//β，故D错误．故选：C．在A中，α与β相交或相行；在B中，α与β不一定垂直；在C中，由由面面垂直的判定定理得α⊥β；在D中，由面面平行的判定定理得α//β．本题考查命题真假的判断，是中档题，解题时要认真审题，注意空间思维能力的培养．5.答案：D解析：本题考查了循环结构的程序框图，属于基础题．模拟程序运行即可求解．解：由程序框图知：程序第一次运行x=3−2=1；第二次运行x=1−2=−1，满足x<0，∴执行y=(−1)3=−1．∴输出−1．故选：D．6.答案：A解析：解：数列{a n}是公差为3的等差数列，{b n}是公差为5的等差数列，∴a n=a1+3(n−1)，b n=b1+5(n−1)，a bn=a1+3(b n−1)=a1+3[b1+5(n−1)−1]=a1+3b1−3+15(n−1)，∴数列{a bn}为公差是15的等差数列．故选：A．数列{a n }是公差为3的等差数列，{b n }是公差为5的等差数列，可得a n =a 1+3(n −1)，b n =b 1+5(n −1)，可得a b n ，即可得出．本题考查了等差数列的定义通项公式，考查了推理能力与计算能力，属于中档题．7.答案：C解析：解：由函数的图象可知：f(1)=0，f(2)=0． 可得：{1+b +c =08+4b +2c =0，解得{b =−3c =2．∴函数f(x)=x 3−3x 2+2x ． 则f′(x)=3x 2−6x +2．令3x 2−6x +2=0.可得：x 1⋅x 2=23． 故选：C ．通过函数的图象求出b ，c ，求出函数的极值点即可求解x 1⋅x 2的值．本题考查函数的导数，函数的极值点的求法，韦达定理的应用，考查计算能力．8.答案：A解析：解：f(x)=asinxcosx −2sin 2x =a 2sin2x +cos2x −1=√a 24+a2√4+1+√4+1)−1， 令cosθ=a2√a 24+1，sinθ=√a 4+1，则tanθ=2a ，其中θ是参数，则f(x)=√a 24+1sin(2x +θ)−1，则函数的最小正周期T =2π2=π，∵直线x =π6是f(x)图象的一条对称轴， ∴2×π6+θ=kπ+π2，即θ=kπ+π6， 则tanθ=tan(kπ+π6)=tan π6=√33，即√33=2a，得a =2√3则函数f(x)的最大值为√a24+1−1=√3+1−1=1，故选：A．利用倍角公式，以及辅助角公式将函数进行化简，进而根据正弦函数的性质求得周期和最小值．本题主要考查了三角函数的性质，利用倍角公式以及辅助角公式进行化简，结合三角函数的对称性求出a的值是解决本题的关键．9.答案：A解析：解：渐近线方程y=±√33x，当过焦点的两条直线与两条渐近线平行时，这两条直线与双曲线右支分别只有一个交点(因为双曲线正在与渐近线无限接近中)，那么在斜率是[−√33,√33]两条直线之间的所有直线中，都与双曲线右支只有一个交点．此直线的斜率的取值范围[−√33,√3 3].故选：A．渐近线方程y=±√33x，当过焦点的两条直线与两条渐近线平行时，这两条直线与双曲线右支分别只有一个交点，由此能求出此直线的斜率的取值范围．本题主要考查直线与圆锥曲线的综合应用能力，具体涉及到直线与双曲线的相关知识，解题时要注意合理地进行等价转化．10.答案：B解析：分析：本题考查概率的求法，考查古典概型、排列组合等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．基本事件总数n=(+)×=50，每所学校男女毕业至少安排一名包含的基本事件m=×()×=20，由此能求出每所学校男女毕业至少安排一名的概率．解答：。

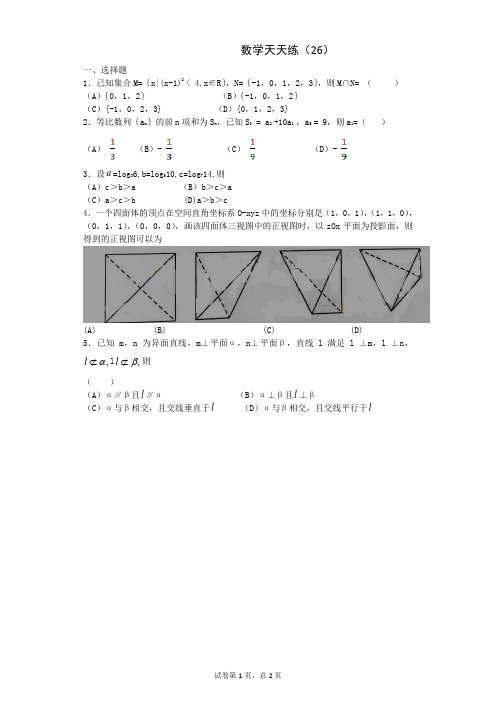
数学天天练（26）一、选择题1．已知集合M=｛x|(x-1)2 < 4,x ∈R ｝，N=｛-1，0，1，2，3｝，则M ∩N= （ ）（A ）｛0，1，2｝ （B ）｛-1，0，1，2｝（C ）{-1，0，2，3} （D ）{0，1，2，3}2．等比数列｛a n ｝的前n 项和为S n ，已知S 3 = a 2 +10a 1 ，a 5 = 9，则a 1=（ ）（A） （B ）- （C） （D ）-3．设a =log 36,b=log 510,c=log 714,则（A ）c ＞b ＞a （B ）b ＞c ＞a（C ）a ＞c ＞b (D)a ＞b ＞c4．一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到的正视图可以为(A) (B) (C) (D)5．已知m ，n 为异面直线，m ⊥平面α，n ⊥平面β，直线l 满足l ⊥m ，l ⊥n ，,l α⊄l ,l β⊄则（ ）（A ）α∥β且l ∥α （B ）α⊥β且l ⊥β（C ）α与β相交，且交线垂直于l （D ）α与β相交，且交线平行于l二、解答题6．如图，直棱柱ABC-111A B C 中，D ，E 分别是AB ，BB1的中点，1AA =AC=CB=（Ⅰ）证明：1BC //平面1ACD ； （Ⅱ）求二面角D-1AC -E 的正弦值.2013年全国新课标二卷数学天天练（26）参考答案1．A【解析】因为集合M=｛x|(x-1)2< 4,x ∈R ｝={}|13x x -<<，N=｛-1，0，1，2，3｝，所以M ∩N=｛0，1，2｝，故选A.【考点定位】本小题主要结合一元二次不等式，考查集合的运算（交集），属容易题，掌握一元二次不等式的解法与集合的基本运算是解答好本类题目的关键.2．C【解析】由S 3 = a 2 +10a 1得，1a +a 2 +a 3= a 2 +10a 1，即a 3= 9a 1，即21a q = 9a 1，解得2q = 9，又因为a 5 = 9，所以41a q = 9，解得119a =，故选C. 【考点定位】本小题主要考查等比数列的通项公式与前n 项和公式,考查数列中基本量的计算，属容易题，掌握等比数列的基础知识是解决好本题的关键.3．D【解析】由题意知：a =log 3631log 2=+211log 3=+,b=log 51051log 2=+211log 5=+,c=log 71471log 2=+211log 7=+,因为2log 3<2log 5<2log 7，所以a ＞b ＞c ，故选D. 【考点定位】本小题主要考查对数的运算、对数换底公式、对数函数的性质等基础知识，属中低档题，熟练对数部分的基础知识是解答好本类题目的关键.4．A【解析】由题意可知：该四面体为正四面体，其中一个顶点在坐标原点，另外三个顶点分别在三个坐标平面内，所以以zOx 平面为投影面，则得到的正视图可以为选项A.【考点定位】本小题主要考查立体几何中三视图的有关知识，考查同学们的空间想象能力，属中档题.5．D【解析】因为m ，n 为异面直线，所以在空间到一点P ，作'm m ，'n n ，则l ⊥'m ，l ⊥'n ，即l 垂直于'm 与'n 确定的平面γ，又m ⊥平面α，n ⊥平面β，所以'm ⊥平面α，'n ⊥平面β，所以平面γ即垂直平面α，又垂直平面β，所以α与β相交，且交线垂直于平面γ，故交线平行于l ，选D.【考点定位】本小题考查空间中线线、线面、面面的位置关系的判断，考查同学们的空间想象与逻辑推理能力等数学基本素养，解答的关键是空间想象力.【答案】（Ⅰ）见解析（Ⅱ）3【解析】（Ⅰ）连结1AC ，交1AC 于点O ，连结DO ，则O 为1AC 的中点，因为D 为AB 的中点，所以OD ∥1BC ，又因为OD ⊂平面1ACD ，1BC ⊄平面1ACD ，所以1BC //平面1ACD ；（Ⅱ）由1AA =AC=CB=2AB 可设：AB=2a ，则1AA ，所以AC ⊥BC ，又因为直棱柱，所以以点C 为坐标原点，分别以直线CA 、CB 、1CC 为x 轴、y 轴、z 轴，建立空间直角坐标系如图，则(0,0,0)C 、1)A 、(,,0)22D 、,)2E ，1)CA = ，CD = ，CE = ，1(,A E = ，设平面1ACD 的法向量为(,,)n x y z = ，则0n CD ⋅= 且10n CA ⋅= ，可解得y x z =-=，令1x =，得平面1ACD 的一个法向量为(1,1,1)n =-- ，同理可得平面1ACE 的一个法向量为(2,1,2)m =- ，则c o s ,n m <>= ，所以s i n ,3n m <>= D-1AC -E 的正弦值为3。

限时训练（二十六） 一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．设复数113iz，21iz，则12zz在复平面内对应的点在( ). A．第一象限 B．第二象限 C．第三象限 D．第四象限

2．设全集是实数集R，22,Mxxx或2430Nxxx，则图中阴影部分所表示的集合 是（ ）.

A. 21xx„ B．22xx剟

C．12xx„ D．2xx 3．已知平面向量2,1a，,2xb，若//ab，则a+b等于( ). A．2,1 B．2,1 C．3,1 D．3,1

4．定义某种运算Sab，运算原理如图所示，则式子15π12tanlnelg10043的值为（ ）.

A．4 B．8 C．11 D．13 5．把边长为1的正方形ABCD沿对角线BD折起，使得平面ABD平面CBD，形成三棱锥ABDC

的正视图与俯视图如图所示，则侧视图的面积为 （ ）.

A.21 B.41 C.42 D.22 6. 已知函数yfxxR满足22fxfx，且1,1x时，1fxx，

UABCDDCBA

俯视图正视图

1111

NMU 则当10,10x时，yfx与4loggxx的图像的交点个数为( ). A.13 B.12 C.11 D.10

7.如图所示, 点,AF分别是双曲线2222:1,0xyCabab的左顶点、右焦点，过点F的直线l与C的

一条渐近线垂直且与另一条渐近线和y轴分别交于,PQ两点．若APAQ，则双曲线C的离心率是( ).

A．2 B．3 C．1134 D．1174 8.在三棱锥PABC中，PA垂直于底面ABC，90ACB，AEPB于E,AFPC

高三数学强化训练〔26〕制卷人：歐陽文化、歐陽理複；制卷時間：二O 二二年二月七日 1.y x y x sin cos ,21cos sin 则=的取值范围是 A 、]21,21[- B 、]21,23[- C 、]23,21[- D 、]1,1[- ∆ABC 中，假设C=2B ，那么b c 的范围是 A 、〔0，2〕 B 、)2,2( C 、)3,2( D 、)3,1([]上交点的个数是，的图象在和ππ22tan sin -==x y x yA 、3B 、5C 、7D 、9()[]上为，在01-x f 等调减函数，又α，β为锐角三角形内角，那么A 、f(cosα)＞ f(cosβ) B、f(sinα)＞ f(sinβ)C 、f(sinα)＜f(cosβ) D、f(sinα)＞ f(cosβ)()[]上为增函数，，在＝函数43sin ,0ππωω->x x f 那么ω的取值范围为 A 、20≤>ω B 、230≤>ω C 、7240≤>ω D 、2≥ωcos y a x b =+的最大值是1，最小值是7-，那么函数cos sin y a x b x =+的最大值是7.给出五个命题：①存在实数α，使1cos sin =αα；②存在实数α，使23cos sin =+αα；③)225sin(x y -=π是偶函数；④8π=x 是函数)452sin(π+=x y 的一条对称轴方程；⑤假设βα,是第一象限角，且βα>，那么βαsin sin >。

其中所有的正确命题的序号是_____。

假设2sin 2αβααβ222sin sin ,sin 3sin +=+则的取值范围是8.函数f(x)=－sin 2x+sinx+a ，〔1〕当f(x)=0有实数解时，求a 的取值范围；〔2〕假设x∈R，有1≤f(x)≤417，求a 的取值范围。

参考答案A CB CB 5 ③④解：〔1〕f(x)=0，即a=sin 2x －sinx=(sinx －21)2－41 ∴当sinx=21时，a min =41，当sinx=－1时，a max =2， ∴a∈[41-，2]为所求 〔2〕由1≤f(x)≤47得⎪⎩⎪⎨⎧+-≥+-≤1sin sin 417sin sin 22x x a x x a ∵ u 1=sin 2x －sinx+2)21(sin 417-=x +4≥4 u 2=sin 2x －sinx+1=43)21(sin 2+-x ≤3 ∴ 3≤a≤4制卷人：歐陽文化、歐陽理複；制卷時間：二O 二二年二月七日。