PUMA560机器人运动学分析

基于MATLAB的PUMA机器人运动仿真研究摘要:机器人运动学是机器人学的一个重要分支,是实现机器人运动控制的基础。

论文以D-H坐标系理论为基础对PUMA560机器人进行了参数设计,利用MATLAB机器人工具箱,对机器人的正运动学、逆运动学、轨迹规划进行了仿真。

Matlab仿真结果说明了所设计的参数的正确性,能够达到预定的目标。

关键词:机器人PUMA560 D-H坐标系运动学轨迹规划机器人运动学的研究涉及大量的数学运算,计算工作相当繁锁。

因此,采用一些工具软件对其分析可大大提高工作效率,增加研究的灵活性和可操作性。

对机器人进行图形仿真,可以将机器人仿真的结果以图形的形式表示出来,从而直观地显示出机器人的运动情况,得到从数据曲线或数据本身难以分析出来的许多重要信息,还可以从图形上看到机器人在一定控制条件下的运动规律[1]。

论文首先设计了PUMA560机器人的各连杆参数,然后讨论了正、逆运动学算法,轨迹规划问题,最后在MATLAB环境下,运用Robotics Toolbox,编制简单的程序语句,快速完成了机器人得运动学仿真。

设机械手起始位置位于A点,qA=[000000],即表示机器人的各关节都处于零位置处。

机械手在B点和C点相对于基坐标系的位姿可用齐次变换矩阵TB和TC来表示。

图2所示为机械手臂在A点时的三维图形。

可通过matlab编程来给出机器人由A运动到B,转动关节2和转动关节3的角度随时间变换的仿真图,如图3所示。

图4所示为末端关节沿x,y,z方向的运动轨迹。

取仿真时间为2s,采样间隔为0.056s。

从图3可以看出:在所取的仿真时间内,转动关节2由零逐渐变化到1.5708rad;转动关节3由零逐渐变化到-1.5708rad。

图4说明机器人由A运动到B,末端关节沿x,y,z方向位移矢量的变化轨迹,证明机器人可以实现不同方位的姿态。

通过仿真曲线可以观察到机器人从A运动到B时各关节的运动情况,且各关节运动情况均为正常,各连杆没有运动错位的情况,从而验证了所有连杆参数的合理性,且说明了各参数的设计能够实现预定的目标。

基于MATLAB的PUMA560机械臂运动仿真徐哲扬来源：?读天下?2021年第10期摘要：工业机器人崛起于在20世纪60，是一种将其和计算机辅助设计〔CAD〕、计算机辅助制造〔CAM〕系统结合在一起的特殊装备。

而Unimation PUMA560作为简单6自由度机器人，在工业中的应用也极为广泛。

本文针对典型的工业机器人Unimation公司生产的PUMA560机器人，运用MATLAB中的机器人仿真工具箱〔Robotics Toolbox〕分析了其正逆运动学方法和轨迹规划的结果，并观察了其运动情况和规律。

关键词：Unimation PUMA560；机械臂；MATLAB仿真机器人运动学涉及大量的算法设计和计算量，所以利用计算机可视化和计算机的仿真软件的方式进行仿真，能过大大减轻科研人员的工作量。

通过图形观察机器人在一定控制条件下的运动规律进而帮助科研人员更好地理解其工作的原理，同时验证其算法的正确性，并对机器人进行图形仿真将结果以图形的形式表示出来，也十分便于展示给企业或者客户。

此外，MATLAB等的仿真软件能在机器人投入生产之前观察其工作效果，从而大大减轻了企业承担的经济风险。

一、搭建PUMA560机械臂本文应用MATLAB的Robotics Toolbox机器人仿真工具箱做机械臂的仿真。

第一步是利用Link函数搭建各个连杆之间关节的相互关系，第二步是调用robot函数创立一个新的机器人对象。

二、 PUMA560的运动分析〔一〕机器人运动学正问题机器人运动学正问题连杆的位移和相对应的关节的偏移量，求解末端连杆坐标系相对于基坐标系的位姿。

图1 PUMA560操作臂运动参数和坐标系分布本文使用MALTBA的Robot中的正问题计算函数fkine能够求解机器人运动学的正问题。

在分析这个问题时，分析可得在操作臂的中部有一个轮子将连续三个部件的运动相关联在一起。

需要根据连杆变换矩阵公式求得每一个连杆的变换矩阵01T～56T，然后将各个连杆矩阵连乘得到06T：〔二〕机器人运动学逆问题机器人运动学逆的解决方法在被告知连杆的位移和相对应坐标系的姿态，即其位姿矩阵，求反求机械臂各个关节的位姿。

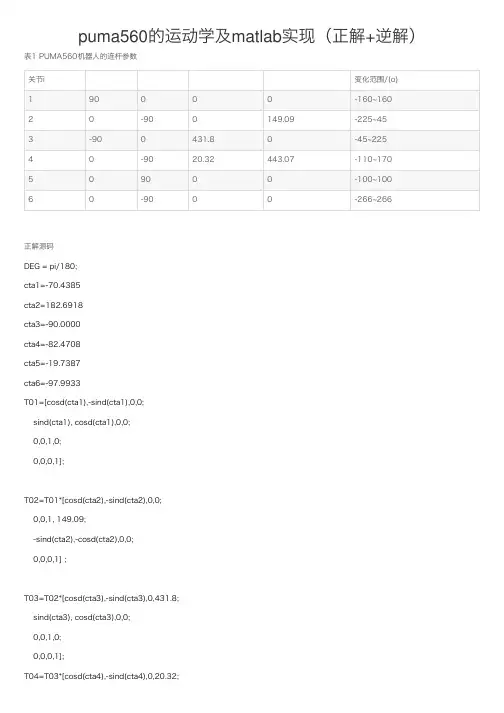
puma560的运动学及matlab实现（正解+逆解）表1 PUMA560机器⼈的连杆参数关节i变化范围/(o) 190000-160~16020-900149.09-225~453-900431.80-45~22540-9020.32443.07-110~170509000-100~10060-9000-266~266正解源码DEG = pi/180;cta1=-70.4385cta2=182.6918cta3=-90.0000cta4=-82.4708cta5=-19.7387cta6=-97.9933T01=[cosd(cta1),-sind(cta1),0,0;sind(cta1), cosd(cta1),0,0;0,0,1,0;0,0,0,1];T02=T01*[cosd(cta2),-sind(cta2),0,0;0,0,1, 149.09;-sind(cta2),-cosd(cta2),0,0;0,0,0,1] ;T03=T02*[cosd(cta3),-sind(cta3),0,431.8;sind(cta3), cosd(cta3),0,0;0,0,1,0;0,0,0,1];T04=T03*[cosd(cta4),-sind(cta4),0,20.32;0,0,1,433.07;-sind(cta4),-cosd(cta4),0,0;0,0,0,1];T05=T04*[cosd(cta5),-sind(cta5),0,0;0,0,-1,0;sind(cta5), cosd(cta5), 0,0;0,0,0,1];T06=T05*[cosd(cta6),-sind(cta6),0,0;0,0,1,0;-sind(cta6),-cosd(cta6),0,0;0,0,0,1];O=T06*[0;0;0;1];=====================================================逆解源码fid = fopen('inverseout.txt','w');%逆解的保存⽂件%赋初值T06 =[0.0000 1.0000 0.0000 -149.0900;0.0000 -0.0000 1.0000 864.8700;1.0000 0 -0.0000 20.3200;0 0 0 1.0000] ;a0=0; a1=0; a2=431.8; a3=20.32; a4=0; a5=0;d1=0; d2=149.09; d3=0; d4=433.07; d5=0; d6=0;n_x=T06(1); n_y=T06(2); n_z=T06(3);o_x=T06(5); o_y=T06(6); o_z=T06(7);a_x=T06(9); a_y=T06(10); a_z=T06(11);p_x=T06(13); p_y=T06(14); p_z=T06(15);disp(['⼋组解分别是：']);for i=1:2for j=1:2for k=1:2%求解theta1(为弧度)sqr1=[sqrt(p_x^2+p_y^2-d2^2),-sqrt(p_x^2+p_y^2-d2^2)];ta1=atan2(p_y,p_x)-atan2(d2,sqr1(i));%求解theta3（弧度表⽰）k1=(p_x^2+p_y^2+p_z^2-a2^2-a3^2-d2^2-d4^2)/(2*a2);sqr3=[sqrt(a3^2+d4^2-k1^2),-sqrt(a3^2+d4^2-k1^2) ];ta3=atan2(a3,d4)-atan2(k1,sqr3(j));fs23=-((a3+a2*cos(ta3))*p_z)+(cos(ta1)*p_x+sin(ta1)*p_y)*(a2*sin(ta3)-d4); sc23=(-d4+a2*sin(ta3))*p_z+(cos(ta1)*p_x+sin(ta1)*p_y)*(a2*cos(ta3)+a3); ta23=atan2( fs23,sc23);%求解theta2 （弧度表⽰）ta2=ta23-ta3;%求解theta4 （弧度表⽰）fs4=[ -a_x*sin(ta1)+a_y*cos(ta1),a_x*sin(ta1)-a_y*cos(ta1)];sc4=[ -a_x*cos(ta1)*cos(ta23)-a_y*sin(ta1)*cos(ta23)+a_z*sin(ta23),a_x*cos(ta1)*cos(ta23)+a_y*sin(ta1)*cos(ta23)-a_z*sin(ta23)];fprintf(fid,'%d,',sc4(1,1));fprintf(fid,'\t');fprintf(fid,'%d,',sc4(2,1));fprintf(fid,'\t');fprintf(fid,'%d,',fs4(1,1));fprintf(fid,'\t');fprintf(fid,'%d,',fs4(1,2));fprintf(fid,'\t');fprintf(fid,'\n');ta4=atan2(fs4(k),sc4(k));%求解theta5 （弧度表⽰）fs5=-a_x*(cos(ta1)*cos(ta23)*cos(ta4)+sin(ta1)*sin(ta4))...-a_y*(sin(ta1)*cos(ta23)*cos(ta4)-cos(ta1)*sin(ta4))...+a_z*(sin(ta23)*cos(ta4));sc5=a_x*(-cos(ta1)*sin(ta23))+a_y*(-sin(ta1)*sin(ta23))+a_z*(-cos(ta23));ta5=atan2(fs5,sc5);%求解theta6 （弧度表⽰）fs6=-n_x*(cos(ta1)*cos(ta23)*sin(ta4)-sin(ta1)*cos(ta4))...-n_y*(sin(ta1)*cos(ta23)*sin(ta4)+cos(ta1)*cos(ta4))...+n_z*(sin(ta23)*sin(ta4));sc6= n_x*(cos(ta1)*cos(ta23)*cos(ta4)+sin(ta1)*sin(ta4))*cos(ta5)... -n_x*cos(ta1)*sin(ta23)*sin(ta5)...+n_y*(sin(ta1)*cos(ta23)*cos(ta4)+cos(ta1)*sin(ta4))*cos(ta5)...-n_y*sin(ta1)*sin(ta23)*sin(ta5)...-n_z*(sin(ta23)*cos(ta4)*cos(ta5)+cos(ta23)*sin(ta5));ta6=atan2(fs6,sc6);%save%将其化为⾓度Theta=[ta1 ta2 ta3 ta4 ta5 ta6]./pi*180endendend关于C++版本的运动学正解和逆解的代码，可以在以下链接下载。

PUMA560机器人运动学分析——基于matlab程序的运动学求解求解PUMA560正向运动学解。

求解PUMA560逆向运动学解。

求解PUMA560的雅克比矩阵。

利用GUI创建运动分析界面。

姓名：xxx学号：201100800406学院：机电与信息工程学院专业：机械设计制造及其自动化年级2011指导教师：xx前言说明此次大作业，是我自己一点一点做的。

程序代码写好之后，感觉只是将代码写上去太过单调，而又不想将课本上或PPT上的基础知识部分复制上去，但我又想让自己的大作业有一点与众不同，所以我决定弄一个GUI界面。

开始对GUI一窍不通，经过几天的学习，终于有了点成果，但还是问题不断，有很多想法却难以去实现，考试在即，只能做成这样了，希望见谅。

目录前言说明 ................................................................................. - 1 -求解PUMA560正向运动学解 ............................................... - 2 -求解PUMA560逆向运动学解 ............................................... - 5 -求解PUMA560的雅克比矩阵 ............................................. - 15 -利用GUI创建运动分析界面................................................ - 22 -求解PUMA560正向运动学解在已知PUMA560各关节连杆DH参数，以及给定相应的关节变量之后，可以通过正向运动学求解出机械手末端抓手在基系内的位姿。

从而利用输入不同的关节变量组合，实现对PUMA560机器人的准确控制。

以下是利用matlab编写的求解PUMA560正向运动学解的函数zhenjie.m:function T=zhenjie(c1,c2,c3,c4,c5,c6)%求puma560正解a2=431.8;a3=20.32;d2=149.09;d4=433.07;c1=c1/180*pi;c2=c2/180*pi;c3=c3/180*pi;c4=c4/180*pi;c5=c5/180*pi;c6=c6/180*pi;A1=[cos(c1),-sin(c1),0,0;sin(c1),cos(c1),0,0;0,0,1,0;0,0,0,1];A2=[cos(c2),-sin(c2),0,0;0,0,1,d2;-sin(c2),-cos(c2),0,0;0,0,0,1];A3=[cos(c3),-sin(c3),0,a2;sin(c3),cos(c3),0,0;0,0,1,0;0,0,0,1];A4=[cos(c4),-sin(c4),0,a3;0,0,1,d4;-sin(c4),-cos(c4),0,0;0,0,0,1];A5= [cos(c5),-sin(c5),0,0;0,0,-1,0;sin(c5),cos(c5),0,0;0,0,0,1];A6=[cos(c6),-sin(c6),0,0;0,0,1,0;-sin(c6),-cos(c6),0,0;0,0,0,1];T=A1*A2*A3*A4*A5*A6end其中c1,c2,c3,c4,c5,c6，为分别输入的各关节变量，即连杆1、连杆2、连杆3、连杆4、连杆5、连杆6的关节转角，直接利用关节矩阵相乘得到机械手末端抓手在基系内的位姿。

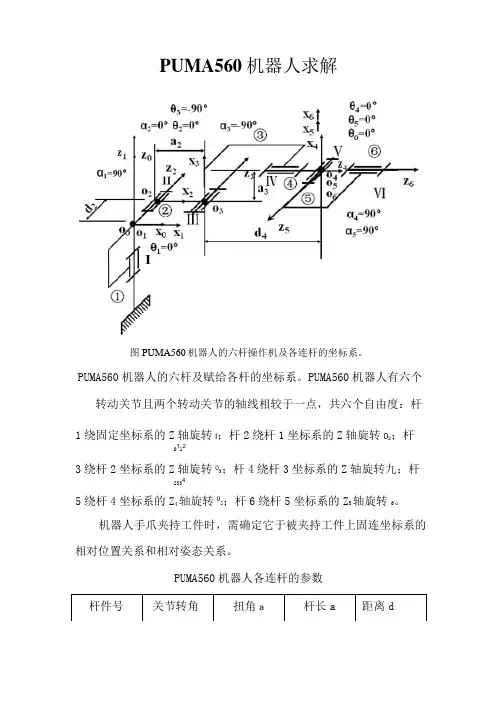
PUMA560机器人求解图PUMA560机器人的六杆操作机及各连杆的坐标系。

PUMA560机器人的六杆及赋给各杆的坐标系。

PUMA560机器人有六个转动关节且两个转动关节的轴线相较于一点，共六个自由度：杆1绕固定坐标系的Z轴旋转l；杆2绕杆1坐标系的Z轴旋转02；杆01 1 23绕杆2坐标系的Z轴旋转03；杆4绕杆3坐标系的Z轴旋转九；杆23345绕杆4坐标系的Z4轴旋转05；杆6绕杆5坐标系的Z5轴旋转°6。

机器人手爪夹持工件时，需确定它于被夹持工件上固连坐标系的相对位置关系和相对姿态关系。

PUMA560机器人各连杆的参数3 -90° -90° 180 04 0° 90° 0 4005 0°90°0 60°根据上表所示的机器人各连杆的参数和齐次变换矩阵公式，可求得T i -1:ic 0-s 0aiii -1T i -1= c a s 0 c a c 0 -s a—ds ai -1i i -1i i -1ii -1is a s 0 s a c 0 c a dc a i -1i i -1ii -1 ii -1L 00 1*:求的所有变换矩阵:00由运动学正解矩阵为:100010 00 01 1080-100000 00 10 01 00001150 -100 001 00180 01400 -100 001 10001000100 -1001356及细化显式公式：nx=c[c(ccc-ss)-ssc]+s(scc+cs) 1245646256145646ny=s[c(ccc-ss)-ssc]-c(scc+cs) 1245646256145646 nz=-s(ccc-ss)-csc245646256 ox=c[c(-ccc-ss)+ssc]+s(cc-scs) 1245646256146456oy=s[c(-ccs-sc)+sss]-c(cc-scs) 1245646256146456 oz=-s(-ccc-ss)+csc 245646256 ax=-c(ccs+sc)-ssc 124525145 ay=-s(ccs+sc)+css 124525145 az=scs-cc24525 px=c[ac+ac-ds]-ds122224221py=s[ac+ac-ds]+dc 122224221pz=-as-as-dc322242 设机器人起始位置为零位如图所示，及图表中各杆的参数得到：一0014800-10150=61001800001该4X 4矩阵即为PUMA560机器人在题目给定情况下的手部的位姿矩阵，即运动学正解。

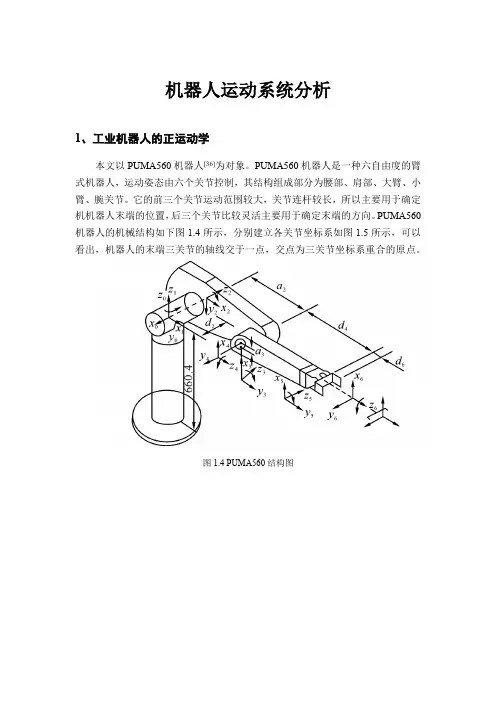
机器人运动系统分析1、工业机器人的正运动学本文以PUMA560机器人[36]为对象。

PUMA560机器人是一种六自由度的臂式机器人，运动姿态由六个关节控制，其结构组成部分为腰部、肩部、大臂、小臂、腕关节。

它的前三个关节运动范围较大，关节连杆较长，所以主要用于确定机机器人末端的位置，后三个关节比较灵活主要用于确定末端的方向。

PUMA560机器人的机械结构如下图1.4所示，分别建立各关节坐标系如图1.5所示，可以看出，机器人的末端三关节的轴线交于一点，交点为三关节坐标系重合的原点。

图1.4 PUMA560结构图图1.5 PUMA560坐标图表1.1为PUMA560机器人的D -H 参数表[37]。

表1.1 PUMA560机器人D -H 参数表表1.1中ιq 列括号里的值为图1.4中机器人关节变量的实际值。

根据齐次坐标变换和表1.1中机器人的参数，得到各连杆的齐次变换矩阵为：112233211233012123224445543445644550000000001000010000010000100010001000001001000000001001；；；；；c s c s c s a s c d s c -s -c c s a c s d -s -c s c ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦--⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦T T T T T 66566000010000001c s -s -c -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦T （1.10）其中，ji T 为坐标系{i}相对于坐标系{j}的齐次变换矩阵；sin i i s q =，cos i i c q =。

将以上各齐次变换矩阵依次相乘即可得到机器人末端相对于操作空间的齐次变化矩阵：0123456123456T =T T T T T T（1.11）式（1.11）为关节变量1q ，2q ，……，6q 的函数。

PUMA560型机器⼈⼀、PUMA560简介PUMA-560机器⼿是⼯业机器⼈, 或称机器⼈操作臂。

从外形来看, 它和⼈的⼿臂相似, 是由⼀系列刚性连杆通过⼀系列柔性关节交替连接⽽成的开式链。

这些连杆就像⼈的⾻架, 分别类似于胸、上臂和下臂, PUMA-560机械⼿的关节相当于⼈的肩关节、肘关节和腕关节。

操作臂的前端装有末端执⾏器或相应的⼯具, 也常称为⼿或⼿⽖。

⼿臂的动作幅度⼀般较⼤,通常实现宏操作。

PUMA⼀560 型机器⼈由机器⼈本体(⼿臂)和计算机控制系统两⼤部分组成。

机器⼈本体(⼿臂): 6 个⾃由度; 驱动采⽤直流伺服电机并配有安全刹闸;⼿腕最⼤载荷为2 kg (包括⼿腕法兰盘); 最⼤抓紧⼒为60 N ; 重复精度为⼠o.lm m; ⼯具在最⼤载荷下的速度: ⾃由运动时为1.0m/s,直线运动时为0.5m/s,⼯具在最⼤载荷下的加速度为1 9 ; 操作范围是以肩部中⼼为球⼼o.92 m 为半径的空间半球; 夹紧系统由压缩空⽓环节与四位电磁阀组成; ⼯具安装表⾯为腕部法兰盘⾯, 安装尺⼨为。

41.3mm上均布4 -M S的安装孔; 整个⼿臂重53kg。

PUMA-560机械⼿的运动学⽅程PUMA-560机械⼿属于关节式的机器⼈, 6个关节都是转动关节。

前⾯3个关节确定⼿腕参考点的位置,后⾯3个关节确定⼿腕的⽅位。

和多数⼯业机器⼈⼀样, 后3个关节轴线交于⼀点。

关节1 的轴线为铅直⽅向, 关节2和关节3的轴线⽔平且平⾏距离为a2, 关节1和关节2的轴线垂直相交,关节3和关节4的轴线垂直交错, 距离为a3。

关节1和2的x轴⽅向的距离为d2, 关节3和4的x 轴⽅向的距离为d4。

PUMA-560机械⼿实体图见图1, 各个连杆坐标系的连杆参数列于表1中。

UMA-560机械⼿实体图⼆、PUMA560机构描述如图1 所⽰，PUMA560 机构是⼀个6 ⾃由度的串联开链式机构。

O-xyz坐标系是基础坐标系,a2, a3, d2,d4是结构参数， (i =1,2,… ,6) 是转⾓，α( i=2,3, …, 6) 是扭⾓。

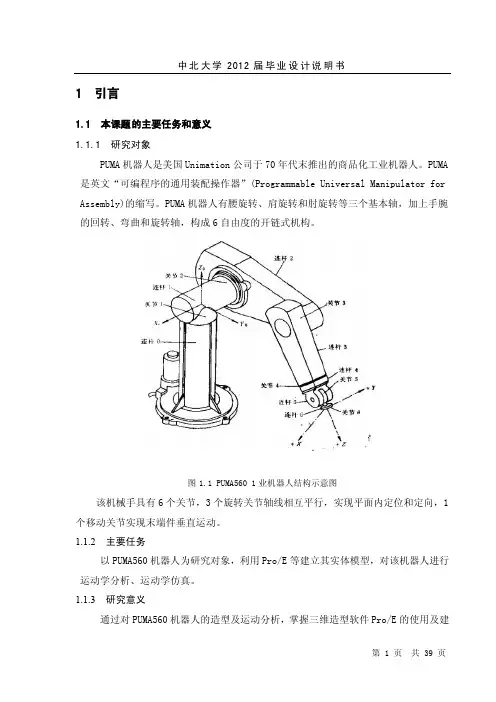
1 引言1.1 本课题的主要任务和意义1.1.1 研究对象PUMA机器人是美国Unimation公司于70年代末推出的商品化工业机器人。

PUMA 是英文“可编程序的通用装配操作器”(Programmable Universal Manipulator for Assembly)的缩写。

PUMA机器人有腰旋转、肩旋转和肘旋转等三个基本轴，加上手腕的回转、弯曲和旋转轴，构成6自由度的开链式机构。

图1.1 PUMA560 1业机器人结构示意图该机械手具有6个关节，3个旋转关节轴线相互平行，实现平面内定位和定向，1个移动关节实现末端件垂直运动。

1.1.2 主要任务以PUMA560机器人为研究对象，利用Pro/E等建立其实体模型，对该机器人进行运动学分析、运动学仿真。

1.1.3 研究意义通过对PUMA560机器人的造型及运动分析，掌握三维造型软件Pro/E的使用及建模的过程，了解该机器人的关节结构、运动学方程及坐标系建立的过程。

1.2工业机器人的相关知识1.2.1工业机器人的概念工业机器人是由各种外部传感器引导，带有一个或多个末端执行器，通过可编程运动，在其工作空间内对真是物体进行操作的、软件可控的机械装置。

1.2.2工业机器人的结构它主要由机械系统(执行系统、驱动系统)、控制检测系统及智能系统组成。

执行系统：执行系统是工业机器人完成抓取工件，实现各种运动所必需的机械部件，它包括手部、腕部、机身等。

手部：机器人为了进行作业而配置的操作机构，又称手爪或抓取机构，它直接抓取工件或夹具。

腕部：又称手腕，是连接手部和臂部的部件，其作用是调整或改变手部的工作方位。

臂部：联接机座和手部的部分，是支承腕部的部件，作用是承受工件的管理管理荷重，改变手部的空间位置，满足机器人的作业空间，将各种载荷传递到机座。

机身：机器人的基础部分，起支撑作用，是支撑手臂的部件，其作用是带动臂部自转、升降或俯仰运动。

驱动系统：为执行系统各部件提供动力，并驱动其动力的装置。

毕业设计(论文)题目 PUMA560机器人的牛顿欧拉逆动力学分析题目：PUMA560机器人的牛顿欧拉逆动力学分析摘要：关键词Title：Abstract：Keywords目录1 前言 (3)1.1选题的背景及意义 (3)1.2国内外发展现状及设计的可行性 (3)1.3 研究的主要内容 (6)1）建立PUMA560机械臂连杆坐标系。

(7)1.3.1 设计要求 (7)2 机械臂运动学 (7)2.1连杆坐标系的确定 (7)2.1.1中间连杆 (7)2.1.2首末连杆 (7)2.2旋转矩阵 (8)2.3连杆变换 (9)3 操作臂动力学 (12)3.1动力学逆问题递推算法 (12)3.2封闭式的动力学方程 (13)4轨迹规划 (13)4.1轨迹规划的插值 (13)4.2三次多项式插值 (14)5总结 (15)致谢 (16)参考文献 (17)1 前言1.1选题的背景及意义机器人，是工业机器人,或称机器人操作臂，机器人臂，机械手等。

从外形来看，他和人的手臂相似，是由一系列刚性连杆通过一系列柔性关节交替连接而成的开式链。

这些连杆就像人的骨架，分别类似于胸(chest)，上臂(upper arm)，和下臂(fore arm)，工业机器人的关节相当于人的肩关节(shoulder)，肘关节(elbow)和腕关节(wrist)。

操作臂的前端装有末端执行器(末端件)(end-effector)或相应的工具(tool)，也常成为手(hand)或手爪(gripper)。

手爪是由两个或多个手指(finger)所组成，手指可以“开”与“合”，实现抓取动作(grasping)和细微操作(fine manipulation）。

手臂的动作幅度一般较大，通常实现宏操作(macro manipulation)。

经过四十多年的发展，工业机器人已在越来越多的领域得到了应用。

在制造业中，尤其是在汽车产业中，工业机器人得到了广泛的应用。

如在毛坯制造(冲压、压铸、锻造等)、机械加工、焊接、热处理、表面涂覆、上下料、装配、检测及仓库堆垛等作业中，机器人都已逐步取代了人工作业。

基于Matlab对于PUMA560机器人的运动空间分析研究沙漠;邓子龙【摘要】通过建立PUMA560机器人空间坐标系并确定连杆参数,利用D-H方法建立了运动学模型,在考虑每个连杆参数边界条件的基础上对其运动学方程求解,利用Robotics Toolbox模块对机器人运动进行了仿真,并利用MATLAB生成机器人工作空间图像,通过图像得到不同步长对于工作空间范围和密度的影响;通过对机器人工作空间及运动轨迹的分析,求得机器人杆长对其工作空间的影响系数,利用MATLAB对不同步长的工作空间范围及密度进行仿真、比较.结果可知:机器人的工作空间是由一近似的椭圆体构成,步长越小,密度与工作空间的精准度越高.为机器人的误差分析和结构优化设计提供理论依据,为机器人的动态控制以及机器人结构的动态特性研究奠定基础.【期刊名称】《机械制造与自动化》【年(卷),期】2016(045)002【总页数】5页(P156-159,183)【关键词】机器人;运动学;工作空间【作者】沙漠;邓子龙【作者单位】辽宁石油化工大学机械工程学院,辽宁抚顺113001;辽宁石油化工大学机械工程学院,辽宁抚顺113001【正文语种】中文【中图分类】TP241近年来，机器人技术在军事、航空航天、工农业生产及医疗等领域迅猛发展。

机器人按技术层次可以分为：固定程序控制机器人、示教再现机器人和智能机器人等。

目前机器人研究涉及到机构学、运动学、控制技术、传感技术等领域[1]。

由于机器人的研究涉及到庞大数学运算，计算工作繁琐复杂，常利用一些工具软件来提高对其分析的工作效率，并且可以增加运算的灵活性和准确性。

现利用MATLAB软件通用性好、计算绘图功能强大等特点，对PUMA560机器人的操作进行运动空间及轨迹的仿真分析得到相关图像数据，以便为实际操作和运算提供参考。

PUMA560机械人末端工作空间代表了机械手的活动范围，是表示机器人工作运动灵活性的一个非常重要指标。

基于MATLAB的puma560型机器人的仿真自121 成佳宇摘要：本文针对PUMA560型机器人，分析了它的正运动学、逆运动学和轨迹规划问题，并在MATLAB环境下，利用机器人仿真工具箱（Robotics Toolbox）对该机器人进行了建模。

同时仿真了正运动学和逆运动学求解和轨迹规划，并观察了各关节运动,得到所需的数据。

说明了所设计的参数是正确的,从而能够达到预定的目标。

关键字：puma560机器人；运动学；MATLAB Robotics Toolbox；仿真Abstract Based on PUMA560 robot, this article analyzes its forward kinematics and inverse kinematics and trajectory planning problem. and in the MATLAB environment, the robot simulation toolkit modeling for the robot. And simulation the forward kinematics and inverse kinematics and trajectory planning as well, observe the movement of each joint, we can get the required data. Shows the designed parameters are correct, so that they can reach a predetermined target. Keyword：PUMA560 robot；kinematics；MATLAB Robotics Toolbox；simulation引言机器人仿真利用计算机可视化和面向对象的手段，模拟机器人的动态特性，帮助研究人员了解机器人工作空间的形态及极限，揭示机构的合理的运动方案和控制算法，并在这台“机器人”上模拟能够实现的功能，使用户直接看到设计效果，及时找出缺点和不足，进行改进，从而解决在机器人设计、制造和运行过程中的问题，避免了直接操作实体可能造成的事故和不必要的损失，这将使机器人的研究和生产进入一个可预知的新时代。

目录一、简介1.1工程背景及参数 (1)二、PUMA 560正解 (3)2.1 求解方法 (3)2.2 程序实现 (4)2.3 正解原程序 (4)三、PUMA 560逆解 (6)3.1 PUMA 560 逆解 (6)3.2 求解过程 (6)3.3 逆解原程序 (9)3.4 程序验证 (10)四、求解PUMA 560雅可比矩阵 (11)4.1 雅可比矩阵简述 (11)4.2 微分变换法求J(q) (11)4.3 矢量积法求J(q) (12)4.4 求解雅可比矩阵 (13)4.5 求解程序 (14)五、PUMA 560运动仿真 (16)PUMA560机器人运动学分析摘要：随着现代工业化的快速发展，机器人得到了广泛应用，有关机器人的理论也一直是研究机器人的重点内容。

本文首先对机器人PUMA560 运动学基础理论进行了必要的描述，建立了 D-H 参数表。

之后根据 D-H 参数表对 PUMA 560 求正解、逆解以及雅可比矩阵。

关键词：机器人PUMA560 正解逆解雅可比Abstract: With the rapid development of modern industrialization, the robot has been widely applied, the robot's theory also has been the research focus of the robot. This article first on PUMA560 robot kinematics basic theory into the necessary description, established the d-h parameters table. Based on d-h parameters after the table of PUMA 560 positive solutions and inverse solution and the jacobian matrix.Key words:Robot PUMA560 Positive solutions Inverse Solution Jacobi一、简介工程背景工业机器人不仅应用于传统制造业如采矿、冶金、石油、化学、船舶等领域，同时也已开始扩大到核能、航空、航天、医药、生化等高科技领域以及家庭清洁、医疗康复、酒店餐饮等服务业领域中。

PUMA560机器人运动学分析PUMA560是一种六轴机器人，由美国Unimation公司于1982年开发生产，具有高精度、高刚度、高速度、高可靠性等特点。

它广泛应用于工业生产线和研究领域，是一种通用性强的机器人。

机械结构PUMA560机器人由机械臂、控制箱和外围设备组成。

机械臂分为一个底座、一个肩部、一个肘部、一个手腕和两个手指。

底座是机械臂的支撑结构，通常固定在地面上，可以旋转360度。

底座上面安装有肩部，肩部可以沿着底座的水平轴向左右旋转170度左右。

肩部上面有肘部，肘部可以沿着肩部的垂直轴向上下旋转150度左右。

肘部上面有手腕，手腕可以沿着肘部的水平轴向左右旋转170度左右。

手腕上面有两个手指，手指之间的距离可以从5.7厘米到15厘米不等。

控制方式PUMA560机器人的控制方式通常分为离线控制和在线控制两种。

离线控制是指事先编写好机器人的运动轨迹，然后通过计算机软件模拟机器人的运动过程，最终生成机器人控制程序。

这种方法可以提高工作效率，缩短生产周期，但是对控制技术的要求较高。

在线控制是指通过外围设备对机器人进行实时控制，实现机器人的运动控制。

这种控制方式虽然灵活方便，但是需要较高的控制精度和反应速度。

运动学分析PUMA560机器人的运动学分析是指研究机器人在空间中的位置和运动。

它通常包括正运动学分析和逆运动学分析两部分。

正运动学分析是指已知机器人各关节的运动角度，计算机器人末端执行器在空间中的位置和姿态。

逆运动学分析是指已知机器人末端执行器在空间中的位置和姿态，计算机器人各关节的运动角度。

正运动学分析采用的是齐次变换矩阵(Homogeneous Transformation Matrix)的方法，即通过多次的旋转和平移变换，将机器人末端执行器的坐标系转换到基坐标系中。

通常可以采用三种方法进行正运动学分析：1. DH法(Denavit-Hartenberg)，该方法是一种广泛应用的方法，能够很好地描述机器人的运动。