PUMA560机器人运动学分析 PPT

机器人技术基础第三章操作臂运动学第三章操作臂运动学1.连杆参数与连杆坐标系2.连杆变换与运动学方程3.XHK 5140换刀机械手的运动学方程4.PUMA 560机器人的运动学方程5.PUMA 560机器人的运动学反解6.腕部三轴相交时的封闭解7.运动学反解的有关问题8.关节空间和操作空间连杆参数与连杆坐标系连杆及其序号关节及其序号关节的种类关节的轴线机械手的结构节拍中间连杆中间连杆的几何描述方法连杆的功能连杆的几何特征尺寸及特征参数a，α例3.1相连中间连杆的连接描述方法转动关节中θ为变量，d为常量。

移动关节中d 为变量，θ为常量。

连杆参数与关节变量第i-1连杆，需要有4个参数：a i-1，αi-1，di-1，θi-1描述。

称为连杆参数。

其中3个为常数，1个为变量。

关节变量qi-1。

n杆机械手，将会有3n常量，n个变量。

n个变量为：q1，q2，… ，q i-1，… ，q n。

记为：[q1，q2，… ，qi-1，… ，qn]T称为：关节向量q，或驱动向量q。

驱动向量q的线性代数空间称为驱动空间，驱动空间是n维空间。

连杆坐标系x 轴的位置：两z 轴相交，两z 轴平行。

两个相邻坐标系之间的关系。

连杆坐标系下连杆参数的正负规定。

连杆1为中间连杆，连杆1的坐标系1可确定，坐标系1在连杆1上，当连杆1运动时坐标系1一起运动。

规定：当t =0时坐标系1的位置为坐标系0的位置，坐标系0的位置永远不动，坐标系0是静止坐标系。

末连杆n规定：当t =0时x n-1的位置为xn的位置。

之后，当qn 变化时xn的位置变化。

PUMA 560机器人的运动学方程。

PUMA560机器人运动学分析——基于matlab程序的运动学求解求解PUMA560正向运动学解。

求解PUMA560逆向运动学解。

求解PUMA560的雅克比矩阵。

利用GUI创建运动分析界面。

姓名：xxx学号：201100800406学院：机电与信息工程学院专业：机械设计制造及其自动化年级2011指导教师：xx前言说明此次大作业，是我自己一点一点做的。

程序代码写好之后，感觉只是将代码写上去太过单调，而又不想将课本上或PPT上的基础知识部分复制上去，但我又想让自己的大作业有一点与众不同，所以我决定弄一个GUI界面。

开始对GUI一窍不通，经过几天的学习，终于有了点成果，但还是问题不断，有很多想法却难以去实现，考试在即，只能做成这样了，希望见谅。

目录前言说明 ................................................................................. - 1 -求解PUMA560正向运动学解 ............................................... - 2 -求解PUMA560逆向运动学解 ............................................... - 5 -求解PUMA560的雅克比矩阵 ............................................. - 15 -利用GUI创建运动分析界面................................................ - 22 -求解PUMA560正向运动学解在已知PUMA560各关节连杆DH参数，以及给定相应的关节变量之后，可以通过正向运动学求解出机械手末端抓手在基系内的位姿。

从而利用输入不同的关节变量组合，实现对PUMA560机器人的准确控制。

以下是利用matlab编写的求解PUMA560正向运动学解的函数zhenjie.m:function T=zhenjie(c1,c2,c3,c4,c5,c6)%求puma560正解a2=431.8;a3=20.32;d2=149.09;d4=433.07;c1=c1/180*pi;c2=c2/180*pi;c3=c3/180*pi;c4=c4/180*pi;c5=c5/180*pi;c6=c6/180*pi;A1=[cos(c1),-sin(c1),0,0;sin(c1),cos(c1),0,0;0,0,1,0;0,0,0,1];A2=[cos(c2),-sin(c2),0,0;0,0,1,d2;-sin(c2),-cos(c2),0,0;0,0,0,1];A3=[cos(c3),-sin(c3),0,a2;sin(c3),cos(c3),0,0;0,0,1,0;0,0,0,1];A4=[cos(c4),-sin(c4),0,a3;0,0,1,d4;-sin(c4),-cos(c4),0,0;0,0,0,1];A5= [cos(c5),-sin(c5),0,0;0,0,-1,0;sin(c5),cos(c5),0,0;0,0,0,1];A6=[cos(c6),-sin(c6),0,0;0,0,1,0;-sin(c6),-cos(c6),0,0;0,0,0,1];T=A1*A2*A3*A4*A5*A6end其中c1,c2,c3,c4,c5,c6，为分别输入的各关节变量，即连杆1、连杆2、连杆3、连杆4、连杆5、连杆6的关节转角，直接利用关节矩阵相乘得到机械手末端抓手在基系内的位姿。

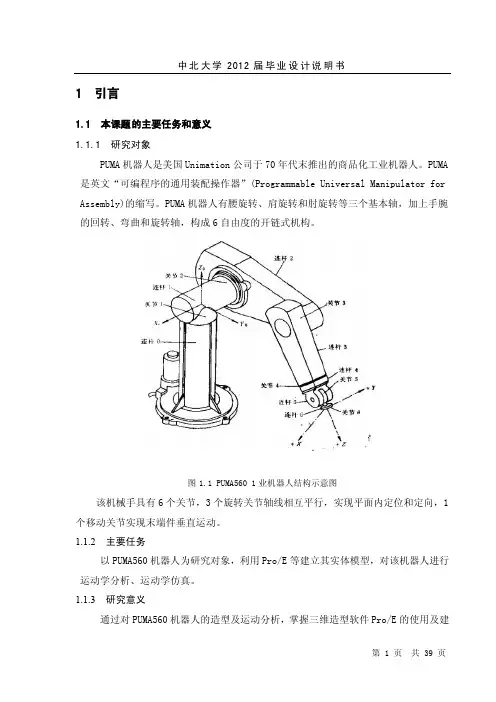
1 引言1.1 本课题的主要任务和意义1.1.1 研究对象PUMA机器人是美国Unimation公司于70年代末推出的商品化工业机器人。

PUMA 是英文“可编程序的通用装配操作器”(Programmable Universal Manipulator for Assembly)的缩写。

PUMA机器人有腰旋转、肩旋转和肘旋转等三个基本轴，加上手腕的回转、弯曲和旋转轴，构成6自由度的开链式机构。

图1.1 PUMA560 1业机器人结构示意图该机械手具有6个关节，3个旋转关节轴线相互平行，实现平面内定位和定向，1个移动关节实现末端件垂直运动。

1.1.2 主要任务以PUMA560机器人为研究对象，利用Pro/E等建立其实体模型，对该机器人进行运动学分析、运动学仿真。

1.1.3 研究意义通过对PUMA560机器人的造型及运动分析，掌握三维造型软件Pro/E的使用及建模的过程，了解该机器人的关节结构、运动学方程及坐标系建立的过程。

1.2工业机器人的相关知识1.2.1工业机器人的概念工业机器人是由各种外部传感器引导，带有一个或多个末端执行器，通过可编程运动，在其工作空间内对真是物体进行操作的、软件可控的机械装置。

1.2.2工业机器人的结构它主要由机械系统(执行系统、驱动系统)、控制检测系统及智能系统组成。

执行系统：执行系统是工业机器人完成抓取工件，实现各种运动所必需的机械部件，它包括手部、腕部、机身等。

手部：机器人为了进行作业而配置的操作机构，又称手爪或抓取机构，它直接抓取工件或夹具。

腕部：又称手腕，是连接手部和臂部的部件，其作用是调整或改变手部的工作方位。

臂部：联接机座和手部的部分，是支承腕部的部件，作用是承受工件的管理管理荷重，改变手部的空间位置，满足机器人的作业空间，将各种载荷传递到机座。

机身：机器人的基础部分，起支撑作用，是支撑手臂的部件，其作用是带动臂部自转、升降或俯仰运动。

驱动系统：为执行系统各部件提供动力，并驱动其动力的装置。

目录一、简介1.1工程背景及参数 (1)二、PUMA 560正解 (3)2.1 求解方法 (3)2.2 程序实现 (4)2.3 正解原程序 (4)三、PUMA 560逆解 (6)3.1 PUMA 560 逆解 (6)3.2 求解过程 (6)3.3 逆解原程序 (9)3.4 程序验证 (10)四、求解PUMA 560雅可比矩阵 (11)4.1 雅可比矩阵简述 (11)4.2 微分变换法求J(q) (11)4.3 矢量积法求J(q) (12)4.4 求解雅可比矩阵 (13)4.5 求解程序 (14)五、PUMA 560运动仿真 (16)PUMA560机器人运动学分析摘要：随着现代工业化的快速发展，机器人得到了广泛应用，有关机器人的理论也一直是研究机器人的重点内容。

本文首先对机器人PUMA560 运动学基础理论进行了必要的描述，建立了 D-H 参数表。

之后根据 D-H 参数表对 PUMA 560 求正解、逆解以及雅可比矩阵。

关键词：机器人PUMA560 正解逆解雅可比Abstract: With the rapid development of modern industrialization, the robot has been widely applied, the robot's theory also has been the research focus of the robot. This article first on PUMA560 robot kinematics basic theory into the necessary description, established the d-h parameters table. Based on d-h parameters after the table of PUMA 560 positive solutions and inverse solution and the jacobian matrix.Key words:Robot PUMA560 Positive solutions Inverse Solution Jacobi一、简介工程背景工业机器人不仅应用于传统制造业如采矿、冶金、石油、化学、船舶等领域，同时也已开始扩大到核能、航空、航天、医药、生化等高科技领域以及家庭清洁、医疗康复、酒店餐饮等服务业领域中。

PUMA560机器人运动学分析PUMA560是一种六轴机器人，由美国Unimation公司于1982年开发生产，具有高精度、高刚度、高速度、高可靠性等特点。

它广泛应用于工业生产线和研究领域，是一种通用性强的机器人。

机械结构PUMA560机器人由机械臂、控制箱和外围设备组成。

机械臂分为一个底座、一个肩部、一个肘部、一个手腕和两个手指。

底座是机械臂的支撑结构，通常固定在地面上，可以旋转360度。

底座上面安装有肩部，肩部可以沿着底座的水平轴向左右旋转170度左右。

肩部上面有肘部，肘部可以沿着肩部的垂直轴向上下旋转150度左右。

肘部上面有手腕，手腕可以沿着肘部的水平轴向左右旋转170度左右。

手腕上面有两个手指，手指之间的距离可以从5.7厘米到15厘米不等。

控制方式PUMA560机器人的控制方式通常分为离线控制和在线控制两种。

离线控制是指事先编写好机器人的运动轨迹，然后通过计算机软件模拟机器人的运动过程，最终生成机器人控制程序。

这种方法可以提高工作效率，缩短生产周期，但是对控制技术的要求较高。

在线控制是指通过外围设备对机器人进行实时控制，实现机器人的运动控制。

这种控制方式虽然灵活方便，但是需要较高的控制精度和反应速度。

运动学分析PUMA560机器人的运动学分析是指研究机器人在空间中的位置和运动。

它通常包括正运动学分析和逆运动学分析两部分。

正运动学分析是指已知机器人各关节的运动角度，计算机器人末端执行器在空间中的位置和姿态。

逆运动学分析是指已知机器人末端执行器在空间中的位置和姿态，计算机器人各关节的运动角度。

正运动学分析采用的是齐次变换矩阵(Homogeneous Transformation Matrix)的方法，即通过多次的旋转和平移变换，将机器人末端执行器的坐标系转换到基坐标系中。

通常可以采用三种方法进行正运动学分析：1. DH法(Denavit-Hartenberg)，该方法是一种广泛应用的方法，能够很好地描述机器人的运动。

PUMA机器人正逆运动学推导及运动空间解算求解：①建立坐标系；②给出D-H参数表；③推导正、逆运动学；④编程得工作空间1.建立坐标系根据PUMA机器人运动自由度，在各关节处建立坐标系如图2所示。

图1 PUMA560机器人坐标系图2.D-H参数表D-H 参数表可根据坐标系设定而得出，见表1。

(1)i θ为绕1i Z -轴从1i X -到i X 的角度； (2)1i α-为绕i X 轴从1i Z -到i Z 的角度；(3)1i a -为沿i X 轴从1i Z -与i X 交点到i O 的距离； (4)i d 为沿1i Z -轴从1i Z -与i X 交点到1i O -的距离。

表1 PUMA 机器人的杆件参数表3. 正运动学推导由坐标系图及各杆件参数可得个连杆变换矩阵。

111101000001100001c s s c T θθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦ 22222222122000010001c s c a s c s a T d θθθθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦3333333323000100001c s c a s c s a T θθθθθθ-⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥⎣⎦ 444434400000100001c s s c T d θθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦5555450000010001c s s c T θθθθ⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦ 66665660000001001c s s c T d θθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦根据各连杆变换矩阵相乘，可以得到PUMA560的机械手变换矩阵，其矩阵为关节变量的函数。

()()()()()()00123456112233445566T T T T T T T θθθθθθ=将上述变换矩阵逐个依次相乘可以得到06T 。

601x x x x yy y y z z z z n o a p n o a p T n o a p ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦()()()()()()()()6514142315236411234651442311523614231446236235452365141423152364112346514423115236x y z x y n c c s s c c c c s s s c s c c s n c c c s c c s s s s s c c c s s n s s s c c s c c s o s c s s c c c c s s c c s c c s o s c c s c c s s s s c =--+-+⎡⎤⎣⎦=+-+-⎡⎤⎣⎦=-+=-+-+⎡⎤⎣⎦=-+-+⎡⎤⎣⎦()()()()()()()()142314623545236423152351414235123514423152345231223232165141423152314231223231265144231z x y z x y c c c s s o s c s c c s c s s a c c s s s s c c c a c s s s c s c c s a a c c s s p c a c a c d s d s s s c c c c c s c d s p s a c a c c d d s c s c c s c -=++=--=++=-=-----+⎡⎤⎣⎦=-++++()512341232342232365234523z s s d s s p c d a s a s d c c c s s ⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪+⎡⎤⎣⎦⎪=-++-⎪⎭上式中()()23232323cos ,sin c s θθθθ=+=+。