-重积分习题课
- 格式:ppt
- 大小:1020.50 KB
- 文档页数:25









第13章重积分§1 有界区域上的重积分1.设一平面薄板(不计其厚度),它在xy平面上的表示是由光滑的简单闭曲线围成的闭区域D.如果该薄板分布有面密度为的电荷,且在D上连续,试用二重积分表示该薄板上的全部电荷.解:设电荷总量为Q,则2.设函数在矩形上有界,而且除了曲线段外,在D上其他点连续.证明f在D上可积.证明:设,将D用平行于两坐标轴的直线分成n个小区域,记,不妨设,将曲线段包含在内,于是在有界闭区域上连续,因此在上可积,即,当时,而当时,取,当时,就有所以f在D上可积.3.按定义计算二重积分,其中解:将D分成n2个小正方形取,则4.设一元函数f(x)在[a,b]上可积,.定义二元函数,证明F(x,y)在D上可积.证明:将[a,b]、[c,d]分别作划分:和则D分成了nm个小矩形记是f(x)在小区间上的振幅,是F在上的振幅,则于是由f(x)在[a,b]上可积,可知,所以即F(x,y)在D上可积.5.设D是R2上的零边界闭区域,二元函数在D上可积.证明和也在D上可积.证明:首先有设,将D划分成n个小区域,利用不等式,可得于是所以由f,g在D上可积,可知即在D上可积.类似地可得从而在D上也可积.§2 重积分的性质与计算1.证明重积分的性质8.证明:不妨设,M、m分别是f(x)在区域Ω上的上确界、下确界,由、性质1和性质3,可得当,积分中值定理显然成立.当,有所以存在,使得即如果f在有界闭区域Ω上连续,由介值定理,存在,使得所以2.根据二重积分的性质,比较下列积分的大小:(1),其中D为x轴、y轴与直线x+y=1所围的区域;(2),其中D为闭矩形[3,5]×[0,1].解:(1)因为在D上成立0<x+y<1,所以,于是(2)因为在D上成立x+y≥3,所以,于是3.用重积分的性质估计下列重积分的值:(1),其中D为闭矩形[0,1]×[0,1];(2),其中D为区域(3),其中Ω为单位球解:(1)因为在D上成立,所以(2)因为在D上成立,所以(3)因为在Ω上成立,所以4.计算下列重积分:(1),其中D为闭矩形[0,1]×[0,1];(2),其中D为闭矩形[a,b]×[c,d];(3),其中Ω为长方体[1,2]×[1,2]×[1,2].解:5.在下列积分中改变累次积分的次序:(改成先y方向,再x方向和z方向的次序积分);(改成先x方向,再y方向和z方向的次序积分).解:6.计算下列重积分:(1),其中D为抛物线和直线所围的区域;(2),其中D为圆心在(a,a),半径为a并且与坐标轴相切的圆周上较短的一段弧和坐标轴所围的区域;(3),其中D为区域(4),其中D为直线和0)所围的区域;(5),其中D为摆线的一拱与x轴所围的区域;(6),其中D为直线和x=1所围的区域;。
重积分典型例题一、二重积分的概念、性质1、二重积分的概念:d 01(,)lim(,)niiii Df x y f λσξησ→==∆∑⎰⎰其中:D :平面有界闭区域,λ:D 中最大的小区域的直径(直径:小区域上任意两点间距离的最大值者),i σ∆:D 中第i 个小区域的面积2、几何意义:当(,)0f x y ≥时,d (,)Df x y σ⎰⎰表示以曲面(,)z f x y =为曲顶,D 为底的曲顶柱体的体积。
所以d 1Dσ⎰⎰表示区域D 的面积。
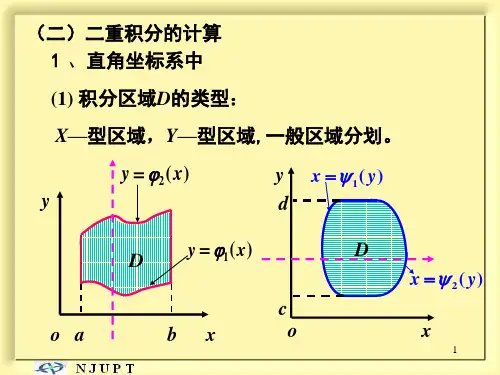
3、性质(与定积分类似)::线性性、对积分区域的可加性、比较性质、估值性质、二重积分中值定理(03年)二、二重积分的计算1、在直角坐标系下计算二重积分(1) 若D 为X 型积分区域:12,()()a x b y x y y x ≤≤≤≤,则21()()(,)(,)by x ay x Df x y dxdy dx f x y dy =⎰⎰⎰⎰(2)若D 为Y 型积分区域:12,()()c y d x y x x y ≤≤≤≤,则21()()(,)(,)dx y cx yf x y dxdy dy f x y dx =⎰⎰(X -型或者Y -型区域之和,如图,则123(,)(,)(,)(,)D D D f x y d x d y f x y d x d y f x y d x d y f x y d x=++⎰⎰⎰⎰⎰⎰⎰(4)被积函数含有绝对值符号时,应将积分区域分割成几个子域,使被积函数在每个子域保持同一符号,以消除被积函数中的绝对值符号。
(5)对称性的应用1(,)2(,),(,)0(,)DD f x y dxdy f x y dxdy f x y y D x f x y y ⎧=⎪⎨⎪⎩⎰⎰⎰⎰关于为偶函数区域关于轴对称, 关于为奇函数1(,)2(,),(,)0(,)DD f x y dxdy f x y dxdy f x y x D y f x y x ⎧=⎪⎨⎪⎩⎰⎰⎰⎰关于为偶函数区域关于轴对称, 关于为奇函数 (6)积分顺序的合理选择:不仅涉及到计算繁简问题,而且又是能否进行计算的问题。