高等数学重积分计算复习
- 格式:ppt
- 大小:1.00 MB
- 文档页数:32

高数大一知识点总结重积分高数大一知识点总结:重积分高等数学中的重积分是一种扩展了二重积分的概念,它在多变量函数的积分中扮演重要的角色。
本文将对高数大一课程中的重积分进行总结和讲解。
一、重积分的概念和性质重积分是定义在三维空间内的函数的积分,通常用来计算多变量函数在某个区域上的累积效应。
与二重积分类似,重积分可以通过分割区域,将其近似为无穷小的小区域,然后对每个小区域进行积分,再将这些积分进行累加而得到。
重积分的计算通常与坐标系的选择有关,常见的坐标系有直角坐标系、极坐标系和柱坐标系等。
根据实际问题的特点和对称性的分析,选择合适的坐标系可以简化计算过程。
在计算重积分时,需要注意积分顺序的选择。
根据题目给定的区域和函数的特点,可以选择先对哪个自变量进行积分,这样有助于简化计算,并得到准确的结果。
重积分具有一些重要的性质,例如线性性、划分性和保号性等。
这些性质在具体计算过程中可以灵活运用,简化计算和分析。
二、重积分的计算方法1. 直角坐标系下的重积分计算方法直角坐标系下的重积分计算通常通过多次积分来实现。
根据题目给定的区域和函数的特点,可以选择先对哪个自变量进行积分,再对另一个自变量进行积分。
通过逐步积分,最终可以得到准确的结果。
2. 极坐标系下的重积分计算方法极坐标系下的重积分计算常常适用于具有旋转对称性的问题。
在极坐标系下,将函数和区域表示成极坐标形式,通过选择合适的积分顺序和极角范围,可以简化计算过程,得到准确的结果。
3. 柱坐标系下的重积分计算方法柱坐标系下的重积分计算通常应用于具有柱对称性的问题。
在柱坐标系下,将函数和区域表示成柱坐标形式,通过选择合适的积分顺序和柱角范围,可以简化计算过程,得到准确的结果。
三、重积分的应用领域重积分在科学和工程领域有广泛的应用。
例如,在物理学中,用重积分可以计算物体的质量、质心和转动惯量等;在电磁学中,可以用重积分计算电荷、电场和电势等;在流体力学中,可以用重积分计算流体的质量、流速和流量等。

高等数学定积分及重积分的方法与技巧第一部分 定积分的计算一、定积分的计算例1 用定积分定义求极限. )0(21lim 1>++++∞→a nn a a a a n . 解 原式=∫∑=⋅=∞→1011lim a ani n x n n i dx =aa x a +=++11111. 例2 求极限 ∫+∞→121lim xx n n dx .解法1 由10≤≤x ,知nn x x x ≤+≤210,于是∫+≤1210x x n ∫≤1n x dx dx .而∫10nx ()∞→→+=+=+n n n x dx n 0111101,由夹逼准则得∫+∞→1021lim xx n n dx =0. 解法2 利用广义积分中值定理()()x g x f ba ∫()()∫=b ax g f dx x dx (其中()x g 在区间[]b a ,上不变号), ().1011112102≤≤+=+∫∫n n nn dx x dx xx x x由于11102≤+≤nx,即211nx+有界,()∞→→+=∫n n dx x n01110,故∫+∞→1021lim x x n n dx =0. 注 (1)当被积函数为()22,x a x R +或()22,a x x R −型可作相应变换.如对积分()∫++3122112xxdx,可设t x tan =;对积分()02202>−∫a dx x ax x a,由于()2222a x a x ax −−=−,可设t a a x sin =−.对积分dx e x ∫−−2ln 021,可设.sin t e x =−(2)()0,cos sin cos sin 2≠++=∫d c dt td t c tb t a I π的积分一般方法如下:将被积函数的分子拆项,[分子]=A[分母]+B[分母]′,可求出22dc bdac A ++=,22dc adbc B +−=. 则积分 ()220cos sin ln 2cos sin cos sin πππtd t c B A dt td t c t d t c B A I ++=+′++=∫.ln2dc B A +=π例3 求定积分()dx x x x ∫−1211arcsin分析 以上积分的被积函数中都含有根式,这是求原函数的障碍.可作适当变换,去掉根式. 解法1 ()dxx x x ∫−1211arcsin 2tx x t ==12121211212arcsin arcsin arcsin 21arcsin 2tt d t dt tt ==−∫∫.1632π=解法2 ()dx x x x∫−1211arcsin .163cos sin cos sin 2sin 2242242πππππ==⋅=∫u du u u uu u u x 小结 (定积分的换元法)定积分与不定积分的换元原则是类似的,但在作定积分换元()t x ϕ=时还应注意:(1)()t x ϕ=应为区间[]βα,上的单值且有连续导数的函数; (2)换限要伴随换元同时进行;(3)求出新的被尽函数的原函数后,无需再回代成原来变量,只要把相应的积分限代入计算即可.例4 计算下列定积分(1)∫+=2031cos sin sin πx x xdx I , dx xx xI ∫+=2032cos sin cos π;(2).1cos 226dx e xx ∫−−+ππ解 (1)∫+=2031cos sin sin πxx xdx I)(sin cos cos 2023du u u uu x −+−=∫ππ=.sin cos cos 223∫=+πI dx xx x故dx xx xx I I ∫++==203321cos sin cos sin 21π=()41cos cos sin sin 212022−=+−∫ππdx x x x x . (2)=I .1cos 226dx e x x ∫−−+ππ()dxe xdu e uu x x u ∫∫−−+=−+−=2262261cos 1cos ππππ+++=∫∫−−2222661cos 1cos 21ππππdx e x dx e x e I x x x.3252214365cos cos 21206226πππππ=×××===∫∫−xdxxdx这里用到了偶函数在对称取间上的积分公式以及公式:dx xdx n n∫∫=2020cos sin ππ()()()()()()=⋅×−×−−=×−×−−=偶数奇数n n n n n n n n n n ,22421331,1322431π小结 (1)常利用线性变换把原积分化为可抵消或可合并的易于积分的形式。


高等数学重积分笔记重积分是高等数学中的一个重要概念,它涉及到空间内某些图形的面积、体积、重量等方面的计算。
以下是一些重积分的笔记内容: 1. 重积分的概念:重积分是一种积分方法,它可以用来计算空间内某些图形的面积、体积、重量等。
重积分的基本思想是将空间内的某个区域分割成多个小区域,然后对每个小区域进行积分。
最终通过求和的方式得到整个区域的面积、体积、重量等。
2. 重积分的基本公式:重积分的基本公式可以用来计算任意函数的重积分。
基本公式如下:∫ABf(x,y)dxdy = ∫ABF(x,y)dydx + ∫BFCA(x,y)dydx - ∫ACBf(x,y)dxdy其中,∫AB 表示空间内某个区域 AB 的面积,f(x,y) 表示区域AB 内的函数值,∫ABF(x,y)dydx 表示区域 AB 内部的函数值,∫BFCA(x,y)dydx 表示区域 AB 外部的函数值,CB 表示区域 AB 的边界。
3. 重积分的应用领域:重积分广泛应用于空间内的图形计算,例如计算球的体积、圆柱的体积、圆锥的体积等。
此外,重积分还可以用于计算曲线的长度、曲线的弧长、函数的极值点等。
4. 重积分的变量替换法:在重积分的计算中,有时候会遇到难以求解的积分,这时可以通过变量替换法来解决。
变量替换法是指将某些变量替换成其他变量,使得积分变得容易求解。
例如,当积分式中含有根号时,可以通过变量替换来解决。
5. 重积分的分部积分法:在重积分的计算中,有时候会遇到难以求解的积分,这时可以通过分部积分法来解决。
分部积分法是指将积分式中的某些变量拆分成两个变量,然后分别进行积分。
例如,当积分式中含有 lnx 时,可以通过分部积分来解决。
以上是重积分的一些笔记内容,希望有所帮助。


高等数学三重积分例题一、计算三重积分∭_varOmega z dV,其中varOmega是由锥面z = √(x^2)+y^{2}与平面z = 1所围成的闭区域。
1. 利用柱坐标计算在柱坐标下x = rcosθ,y = rsinθ,z = z,dV = rdzdrdθ。
锥面z=√(x^2)+y^{2}在柱坐标下就是z = r。
由锥面z = r与平面z = 1所围成的闭区域varOmega,其在柱坐标下的范围为:0≤slantθ≤slant2π,0≤slant r≤slant1,r≤slant z≤slant1。
2. 计算积分则∭_varOmegaz dV=∫_0^2πdθ∫_0^1rdr∫_r^1zdz。
先计算关于z的积分:∫_r^1zdz=(1)/(2)(1 r^2)。
再计算关于r的积分:∫_0^1r×(1)/(2)(1 r^2)dr=(1)/(2)∫_0^1(rr^3)dr=(1)/(2)((1)/(2)-(1)/(4))=(1)/(8)。
最后计算关于θ的积分:∫_0^2πdθ = 2π。
所以∭_varOmegaz dV=(1)/(8)×2π=(π)/(4)。
二、计算三重积分∭_varOmega(x + y+z)dV,其中varOmega是由平面x = 0,y = 0,z = 0及x + y+z = 1所围成的四面体。
1. 利用直角坐标计算对于由平面x = 0,y = 0,z = 0及x + y + z=1所围成的四面体varOmega,其范围为0≤slant x≤slant1,0≤slant y≤slant1 x,0≤slant z≤slant1 x y。
则∭_varOmega(x + y + z)dV=∫_0^1dx∫_0^1 xdy∫_0^1 x y(x + y + z)dz。
2. 计算积分先计算关于z的积分:∫_0^1 x y(x + y+z)dz=(x + y)z+(1)/(2)z^2big|_0^1 x y=(x + y)(1 x y)+(1)/(2)(1 x y)^2展开得x + y-(x^2+2xy + y^2)+(1)/(2)(1 2x 2y+x^2+2xy + y^2)进一步化简为x + y x^2-2xy y^2+(1)/(2)-x y+(1)/(2)x^2+xy+(1)/(2)y^2即(1)/(2)-x^2-xy (1)/(2)y^2。
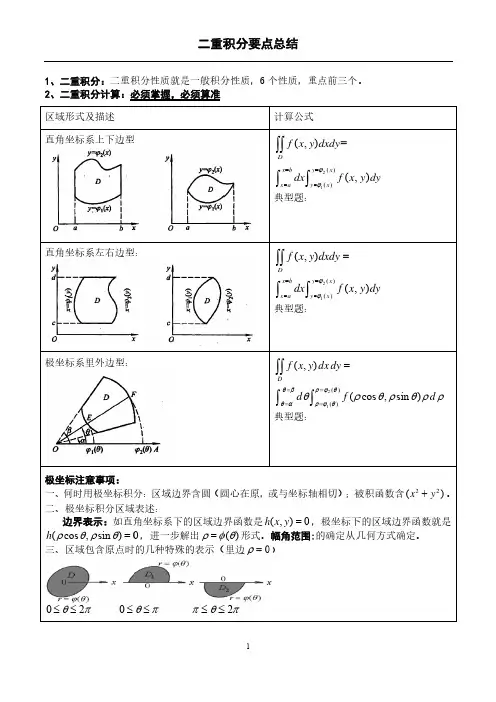


重积分知识点重积分是数学分析中的一个重要概念,是对多元函数在三维空间中的积分,也称为三重积分。
它是高等数学、微积分、物理学等领域中必须掌握的基本知识点。
下面将从定义、性质、计算方法和应用四个方面详细介绍重积分知识点。
一、定义重积分是对三元函数在三维空间中某一区域内的积分,表示为:$$\iiint_{\Omega}f(x,y,z)dV$$其中,$\Omega$表示被积区域,$dV$表示体积元素。
二、性质1.线性性质:若$f(x,y,z)$和$g(x,y,z)$在$\Omega$上可积,则有:$$\iiint_{\Omega}(af+bg)dV=a\iiint_{\Omega}f(x,y,z)dV+b\iiint_{ \Omega}g(x,y,z)dV$$其中$a,b$为常数。
2.可加性质:若将$\Omega$划分成若干个互不相交的子区域$\Omega_1,\Omega_2,...,\Omega_n$,则有:$$\iiint_{\Omega}f(x,y,z)dV=\sum^n_{i=1}\iiint_{\Omega_i}f(x,y,z )dV$$3.保号性质:若$f(x,y,z)\geq0$在$\Omega$上成立,则有:$$\iiint_{\Omega}f(x,y,z)dV\geq0$$4.单调性质:若$f(x,y,z)\leq g(x,y,z)$在$\Omega$上成立,则有:$$\iiint_{\Omega}f(x,y,z)dV\leq\iiint_{\Omega}g(x,y,z)dV$$三、计算方法1.直接计算法:将被积函数$f(x,y,z)$转化为三元积分的形式,然后按照定积分的方法进行计算。
2.累次积分法:将三重积分转化为三个定积分的累次积分,然后按照定积分的方法进行计算。
3.极坐标法:适用于旋转对称的区域,可以通过极坐标系下的面积元素$dS$和体积元素$dV$来简化计算。
4.柱面坐标法:适用于柱面对称的区域,可以通过柱面坐标系下的面积元素$dS$和体积元素$dV$来简化计算。

高考数学知识点精讲重积分与曲线积分的计算高考数学知识点精讲:重积分与曲线积分的计算在高考数学中,重积分与曲线积分是较为复杂但又十分重要的知识点。
理解和掌握它们的计算方法,对于解决许多数学问题以及在后续的高等数学学习中都具有关键意义。
一、重积分重积分包括二重积分和三重积分。
1、二重积分二重积分的几何意义是计算以给定的二元函数为曲顶的曲顶柱体的体积。
其计算的基本思想是将区域分割成小的矩形,然后对每个小矩形上的函数值进行近似求和,当分割越来越细时,这个和就趋近于二重积分的值。
在直角坐标系下,计算二重积分通常有两种积分顺序:先对 x 积分再对 y 积分,或者先对 y 积分再对 x 积分。
选择合适的积分顺序往往能简化计算。
例如,对于函数\(f(x,y)\)在区域\(D\)上的二重积分,若\(D\)可以表示为\(a\leq x\leq b\),\(\varphi_1(x)\leqy\leq \varphi_2(x)\),则先对\(y\)积分,化为累次积分:\\iint_D f(x,y)dxdy =\int_a^b\!\!\left\int_{\varphi_1(x)}^{\varphi_2(x)} f(x,y)dy\rightdx\若\(D\)可以表示为\(c\leq y\leq d\),\(\psi_1(y)\leq x\leq \psi_2(y)\),则先对\(x\)积分,化为累次积分:\\iint_D f(x,y)dxdy =\int_c^d\!\!\left\int_{\psi_1(y)}^{\psi_2(y)} f(x,y)dx\rightdy\在极坐标系下,若\(f(x,y) = f(\rho\cos\theta, \rho\sin\theta)\),区域\(D\)由极坐标方程表示,则二重积分可以化为:\\iint_D f(x,y)dxdy =\int_{\alpha}^{\beta}\!\!\int_{r_1(\theta)}^{r_2(\theta)} f(\rho\cos\theta, \rho\sin\theta)\rho d\rho d\theta\2、三重积分三重积分的几何意义是计算空间立体的质量。
大一高数重积分知识点重积分是高等数学中的重要概念,主要是对二重积分的推广和拓展。
在本篇文章中,将介绍一些大一高数课程中涉及的重积分的基本知识点和相关概念。
一、重积分的概念重积分是对多变量函数在某个区域上的积分,主要用于计算空间内的体积、重心以及质心等物理量。
在二维情况下,重积分被称为二重积分,表示对平面上的区域进行积分;在三维情况下,重积分被称为三重积分,表示对空间内的区域进行积分。
二、二重积分的计算对于二重积分的计算,常用的方法有直角坐标法和极坐标法。
1. 直角坐标法通过将二重积分化为两个一重积分的形式来计算。
例如,对于函数f(x, y),其在矩形区域D上的二重积分可以表示为:∬D f(x, y) dxdy通过确定积分的上下限,将二重积分转化为两个单变量函数的积分。
2. 极坐标法对于具有极坐标对称性的函数,可以采用极坐标来进行计算。
通过将二重积分转化为极坐标下的一重积分,可以简化计算过程。
三、三重积分的计算对于三重积分的计算,也可以采用直角坐标法或柱坐标法进行计算。
1. 直角坐标法对于函数f(x, y, z),其在空间内的三重积分可以表示为:∭E f(x, y, z) dxdydz通过逐次进行积分,将三重积分转化为三个一重积分的形式。
2. 柱坐标法对于具有柱坐标对称性的函数,可以采用柱坐标来进行计算。
通过将三重积分转化为柱坐标下的一重积分,可以简化计算过程。
四、变量替换法在计算重积分时,有时可以通过变量替换法来简化积分的计算过程。
通过适当选择变量替换,可以将原先复杂的积分问题转化为更简单的形式。
变量替换法在求解一些特殊的积分问题时非常有用。
五、应用领域重积分在物理学、工程学等领域中具有广泛的应用。
在物理学中,通过重积分可以计算物体的质量、质心、转动惯量等物理量。
在工程学中,通过重积分可以计算流体的流量、电荷分布等问题。
总结:大一高数课程中的重积分是深入学习积分学的重要内容,涵盖了二重积分和三重积分的计算方法,以及变量替换法的应用。
高数大一知识点三重积分高等数学是大学数学专业的一门重要课程,对于数学专业的学生来说,掌握高数知识点是非常重要的。
在大一的高等数学课程中,三重积分是一个非常重要的知识点。
下面将从基本概念、计算方法和应用等几个方面来介绍三重积分。
一、基本概念三重积分是对三维空间中的函数进行积分运算。
如果一个三维空间中的函数在某个区域上是连续的,那么可以对这个函数进行三重积分。
三重积分可以看作是对空间中的体积进行求和的过程。
在三重积分中,我们需要确定积分函数、积分区域、积分方向和积分顺序等要素。
二、计算方法三重积分的计算方法有直接计算法和间接计算法两种。
直接计算法是将积分区域划分成小的立体元,然后对每个立体元进行积分计算,最后将所有立体元的积分结果相加得到最终的积分结果。
间接计算法是利用高斯公式和格林公式来进行计算。
高斯公式是将三重积分转化为对闭合曲面上的二重积分,然后再将二重积分转化为对曲线上的一重积分。
格林公式则是将曲线积分转化为坐标轴上的一重积分。
利用这两个公式,可以将三重积分的计算转化为一重积分的计算,简化了计算的步骤。
三、应用三重积分在物理学、工程学和计算机图形学等领域有着广泛的应用。
在物理学中,三重积分可以用来计算物体的质量、重心、转动惯量等物理量。
例如,在力学中,我们可以通过对物体密度分布函数进行三重积分来计算物体的质量。
在工程学中,三重积分可以用来计算物体的体积、质量、质心等。
例如,在建筑工程中,我们可以通过对建筑结构进行三重积分来计算结构的体积和质量。
在计算机图形学中,三维模型的表面可以通过三重积分来进行渲染和着色。
例如,通过对三维物体的颜色分布进行三重积分,可以得到物体在不同方向上的颜色分布,从而实现逼真的渲染效果。
四、总结三重积分是大一高等数学中的一个重要知识点,掌握三重积分的基本概念、计算方法和应用是非常重要的。
通过对三重积分的学习和应用,可以提高数学建模和问题求解的能力,并在物理学、工程学和计算机图形学等领域中发挥重要作用。
高等数学重积分求解题技巧高等数学中的重积分是一种对多变量函数进行积分运算的方法,其求解需要掌握一定的技巧。
下面我将介绍一些常用的高等数学重积分求解题技巧。
一、确定积分区域在求解重积分时,首先需要确定积分区域。
常用的方法有:图形法、参数方程法、立体体积法、坐标轴法等。
根据题目给出的条件,选择合适的方法确定积分区域。
二、确定积分次序在确定积分次序时,需要考虑到函数在积分区域上的表达式。
通常可以将多变量函数的积分次序调整为适合计算的方式。
常用的方法有:先积x后积y、先积y后积x、极坐标系下积分等。
三、利用对称性在一些情况下,积分区域具有对称性,可以利用对称性简化求解过程。
例如,当积分区域关于x轴对称时,可以将积分区域进行对称延拓,然后将求解的结果乘以2。
利用对称性可以减少计算量,加快解题速度。
四、变量代换在求解一些复杂的重积分时,可以采用变量代换的方法进行简化。
变量代换可以将复杂的积分转化为简单的形式。
常见的变量代换有:平铺代换、柱坐标代换、球坐标代换等。
选择合适的变量代换可以使原始的积分更容易计算。
五、利用奇偶性在一些情况下,被积函数具有奇偶性。
可以利用奇偶性进行简化。
例如,当被积函数为奇函数时,其在对称区域上的积分结果为0,只需要计算对称区域上的一个部分即可。
六、利用分部积分在求解重积分时,可以利用分部积分的方法进行简化。
分部积分可以将积分的被积函数分解为两个因子之积,然后进行积分操作。
通过反复应用分部积分法,可以逐步简化积分表达式。
七、利用定积分的性质重积分实际上可以看作多个定积分的组合。
因此,可以运用定积分的性质进行求解。
例如,定积分可以与求导、极限运算交换次序,可以通过定积分的积分区间的变化进行转化等。
八、利用对数、指数性质在一些特殊情况下,重积分可以转化为对数、指数的形式。
可以利用对数、指数的性质进行求解。
例如,当积分的被积函数具有指数型形式时,可以利用指数函数的积分性质进行简化。
九、利用对数函数的导数当被积函数可以表示为某个对数函数的导数时,可以利用对数函数的导数来简化积分过程。
4. :x2A.5.A. C.A)B)C)D) y2 z2B.{(x,y) x2a22r0 sinxyxyxyxyxcosxcosxcosxyxyxyxcos xydxdydxdydxdydxdyzln(x2C. 0x22y2cos2a2,y 0},其中dr B. 0da 0( r3sin cos )dr D. 02d2 xydxdyD12 xcos xy dxdy D12 (xy xcos(xy))dxdy D1z2 1) dxdydzz2 1D.0,则3r sina3r sin43xy dcoscosdrdr - a3r sin cos dr 第九章重积分一选择题1.I= (x2y2z2)dv, :x2y2z21球面内部,则= [ C ]A.dv 的体积22B. 2 d 2 d001r40 sin drC. 202 d 014d r sin dr 0 2D. d d 00 01r4 sin dr2.是x=0, y=0, z=0, x+2y+z=1 所围闭区域,则xdxdydz [ B ]则[B ] 1 1 2x 1 x 2yA. 0dx 0 dy 0 xdzB. 0dx 1 x dy 0102x 2y xdzC. 02dy 1 y102 dx 0xdzD. 01dy 2y dx 1 x 2y0 xdz3. 设区域D 由直线y x, y x 和x 1 所围闭区域,D1是D 位于第一象限的部分,22 x 28.交换二次积分 2dx x f (x, y)dy 的积分顺序为( A )A.aB. 12 a2C. a 2D.7.积分 2 dcos 0 f (r cos ,r sin )rdr 可写为D1 y y 21 1 y 2A.dy 0 0f (x,y)dxB. dy00 f (x,y)dx111 x x 2B.dx 00 f (x,y)dyD. dx00f ( x, y)dy6.设 a 0, f(x) g(x) 42(A) dy yf ( x, y)dx y2x 2f (x,y)dx 04 (C) 0dy(B) (D) 9.设平面区域D 由 x 0,0,14 , x I 2 (x D y)3dxdy, I 3[sin( xD(A) I 1I 2I 3 (B)I 3I 2 I110. y 2 41x 大于零 11.设积分区域 (A) 22sin x y 22 xy(B) 小于零 D 由|x| a,|y| dxdy 的值 a(a (A)1(B) 14 4dy4dyyf (x, y)dxy2f (x, y)dxy 1围成,若 I 1[ln(x y)]3dxdy,D则I 1,I 2, I 3的大小顺序为( C ). y)]3dxd y, (C) I 1B ). (C) 00)围成, (C) 0I 3 I 2(D) I 3 I 1 I 2(D) 不能确定 xydxdy ( C ).(D) A, B, C 都不对12.1(A) 大于零13.把二次积分 1 dx 0 22y dxdy的值y 2(B) 小于零1 x2 x 2 y 2 1 x 2e B ).(C) 0 (D) 不能确定 dy 化为极坐标形式的二次积分( B ). (A ) re r dr21 r 2(B) d 0re r dr (C) 2d212e rdr 02 (D) 0 d12e r dr 0a,0 x 1 ,D 为全平面,则 f (x)g(y x)dxdy C 0, 其余 Ddxdy 14. 设积分区域D是由直线y=x,y=0,x=1 围成,则有D( A )1 x 1 ydx d ydy dx(A )0(B )011ydx d ydy dx(C )0x(D )0x15. 设 D 由y x, y2x,ydxdy1围成,则 D( B)113 (A ) 2 (B 4(C )1D ) 216.根据二重积分的几何意义,下列不等式中正确的是 ( B ); (A ) (x 1)d 0,D : x ≤1, y ≤1;(B ) (x 1)d 0,D : x ≤1, y ≤1;DD11(A ) 1 ( B ) 2 (C ) 4 (D )219.x 2 y 2 13 x 2 y 2dxdy 的值等A)xy13 6C.6;D.3 A. ; B.4752xydxdy0x120. 二重积分 0 y 1(C )11(A )1 ( B ) 2(C ) 4(D )22x,y |x22y a , 又有2x2y dxdy 821. 设D 是区域D,则 a=( B )(A 1(B ) 2 (C )4(D )8(C) ( x 2 D y 2)d0,D : x 2 y2 ≤17.x 2y 2 dxdy ( C ), D(A)2πdr 2dr 1(C) 2 π2d 012r dr ;18. xydxdy0x1二重积分 0 y 1(C )1;(D) ln(x 2 y 2)d0,D : x+ y ≤1D 22D :1≤ x 2 y 2 ≤4;2 π4(B) 0 d 1 rdr ;012 π2(D) d r dr22. 若D 是平面区域 x,y |0 x1, 1 ye ,则二重积分 xdxdy D y三、计算与证明2. 计算 I= sin x 2 y 2 dxdy , D={(x, y) D解:令 x=rcos , y=rsine1(A ) 2(B )2(C ) e 23. 设D 由 y x,y 2x,y 1 围成,则 11(A ) 2(B )4 (C )1二、填空题1.变换积分次序0 22dy 1 y 2 2 dy 0f (x,y) dx(D ) 1 dxdyD (B )3(D ) 2221 1 x2 2dx 02 f(x, y)dy2dx 0f (x,y)dy2.D 是以 (0,0),(1, 1),(1,1) 为顶点的三角形3. 4.5. 6、7、 (x 2 y 2)dxdyD1变换积分次序 12dyx 2 y 2dxdy D 4 y 2f(x,y)dxy 2交换二次积分的积分次序 2xdx 11121 x 4 1dx xf (x, y)dy 1dx xf (x,y)dy42f x,y dy= dy f x, y dx1y交换 dy e x dx 的积分次序后的积分式为1 x 1dx 0e x dy ,其积分值为 12 e 1交换二次积分的积分次序后, 交换二次积分的次序1 dx 01 1 yf (x ,y)dy= 0dy 0 f (x,y)dxa 2ax x 2dx0xf ( x, y)dyaydy aa 2 y 2f(x,y)dx1. 计算xy 2dxdy, 其中 DD 是抛物线 y 2=2x1与直线 x= 1 所围闭区域121解: xy 2dxdy = 1dy 21D 2yxy 2dx112 (y 18 12118 y 6 )dy 8 2x 2 y24 2}比较大小:则 I==623. 设 G(x)在 0 x 1上有连续的 G ''(x) , 求 I= xyG ''(x 2 y 2 )dxdy , 其中 D 为 D x 2 y 2 1的第一象限部分解:在极坐标下计算积分, D={(r, ) 0 r 1,0 }22 '' 2 I= r sin cos G (r )rdrd D=1 1r 3G ''(r 2)dr201 1 '' = 1uG '' (u)du401'= [G '(1) G (0) G(1)] 44. xy dxdy,其中 是以 a 为半径,坐标原点为圆心的圆4x 2 )xdx ( 1 分) = 2解:xy dxdy=a a(a 2 x 2) x dx =5.sin x 2 y 2 dxdy 解:sin x 2 y 2dxdy =x 2y 2 42r sin rdr =22r sin rdr6.ze (x 2 y622z )dxdydz ,其中为球体x 2 y 2 z 21在 z 0 上的部分。