标题-2017-2018学年高中数学三维设计苏教版必修5：课时跟踪检测(十一) 等比数列的性质

课时跟踪检测（十）等比数列的概念及通项公式层级一学业水平达标1．2＋3和2－3的等比中项是()A．1B．－1C．±1D．2解析：选C设2＋3和2－3的等比中项为G，则G 2＝(2＋3)(2－3)＝1，∴G＝±1.2．在首项a1＝1，公比q＝2的等比数列{a n}中，当a n＝64时，项数n等于()A．4 B．5C．6 D．7解析：选D因为a n＝a1q n－1，所以1×2n－1＝64，即2n－1＝26，得n－1＝6，解得n＝7.3．设等差数列{a n}的公差d不为0，a1＝9d，若a k是a1与a2k的等比中项，则k等于() A．2 B．4C．6 D．8解析：选B∵a n＝(n＋8)d，又∵a2k＝a1·a2k，∴[(k＋8)d]2＝9d·(2k＋8)d，解得k＝－2(舍去)或k＝4.4．等比数列{a n}的公比为q，且|q|≠1，a1＝－1，若a m＝a1·a2·a3·a4·a5，则m等于()A．9 B．10C．11 D．12解析：选C∵a1·a2·a3·a4·a5＝a1·a1q·a1q2·a1q3·a1q4＝a51·q10＝－q10，a m＝a1q m－1＝－q m－1，∴－q10＝－q m－1，∴10＝m－1，∴m＝11.5．等比数列{a n}中，|a1|＝1，a5＝－8a2，a5＞a2，则a n等于()A．(－2)n－1 B．－(－2n－1)C．(－2)n D．－(－2)n解析：选A设公比为q，则a1q4＝－8a1q，又a1≠0，q≠0，所以q3＝－8，q＝－2，又a5＞a2，所以a2＜0，a5＞0，从而a1＞0，即a1＝1，故a n＝(－2)n－1.6．等比数列{a n}中，a1＝－2，a3＝－8，则a n＝________.1a3 －8解析：∵＝q2，∴q2＝＝4，即q＝±2.a1 －2当q＝－2时，a n＝a1q n－1＝－2×(－2)n－1＝(－2)n；当q＝2时，a n＝a1q n－1＝－2×2n－1＝－2n.答案：(－2)n或－2n1 a8＋a97．已知等比数列{a n}的各项均为正数，且a1，a3,2a2成等差数列，则＝________.2 a6＋a71解析：由题设a1，a3,2a2成等差数列可得a1＋2a2＝a3，即q2－2q－1＝0，所以q＝2＋2a8＋a9 a81＋q1，＝＝q2＝3＋2 2.a6＋a7 a61＋q答案：3＋2 28．已知三个数成等比数列，其积为512，如果第一个数与第三个数各减去2，则此时的三个数成等差数列，则原来的三个数的和等于________．a 解析：依题意设原来的三个数依次为，a，aq.qa∵·a·aq＝512，∴a＝8.q又∵第一个数与第三个数各减去2后的三个数成等差数列，a∴(－2 )＋(aq－2)＝2a，q1∴2q2－5q＋2＝0，∴q＝2或q＝，2∴原来的三个数为4,8,16或16,8,4.∵4＋8＋16＝16＋8＋4＝28，∴原来的三个数的和等于28.答案：289．在四个正数中，前三个成等差数列，和为48，后三个成等比数列，积为8 000，求这四个数．解：设前三个数分别为a－d，a，a＋d，则有(a－d)＋a＋(a＋d)＝48，即a＝16.b 设后三个数分别为，b，bq，则有qb·b·bq＝b3＝8 000，即b＝20，q∴这四个数分别为m,16,20，n，202∴m＝2×16－20＝12，n＝＝25.162即所求的四个数分别为12,16,20,25.10．已知递增的等比数列{a n}满足a2＋a3＋a4＝28，且a3＋2是a2和a4的等差中项，求a n.解：设等比数列{a n}的公比为q.依题意，知2(a3＋2)＝a2＋a4，∴a2＋a3＋a4＝3a3＋4＝28，∴a3＝8，a2＋a4＝20，8 1∴＋8q＝20，解得q＝2或q＝(舍去)．q 2a3又a1＝＝2，∴a n＝2n.q2层级二应试能力达标2a1＋a21．设a1，a2，a3，a4成等比数列，其公比为2，则的值为()2a3＋a41 1A. B.4 21C. D．182a1＋a2 1 1解析：选A原式＝＝＝.q22a1＋a2q2 412．在等比数列{a n}中，已知a1＝，a5＝3，则a3＝()3A．1 B．3C．±1D．±31 解析：选A由a5＝a1·q4＝3，所以q4＝9，得q2＝3，a3＝a1·q2＝×3＝1.33．设a1＝2，数列{1＋2a n}是公比为3的等比数列，则a6等于()A．607.5 B．608C．607 D．159解析：选C∵1＋2a n＝(1＋2a1)×3n－1，5 × 243－1 ∴1＋2a6＝5×35，∴a6＝＝607.24．如图给出了一个“三角形数阵”．已知每一列数成等差数列，从第三行起，每一行数成等比数列，而且每一行的公比都相等，141 1，2 433 3 3，，4 8 16…记第i行第j列的数为a ij(i，j∈N*)，则a53的值为()1 1A. B.16 85 5C. D.16 41 1 1 1 5 解析：选C第一列构成首项为，公差为的等差数列，所以a51＝＋(5－1)×＝.又4 4 4 4 45因为从第三行起每一行数成等比数列，而且每一行的公比都相等，所以第5行构成首项为，41 5 1 5公比为的等比数列，所以a53＝4×(2 )2＝.2 165．若数列{a n}的前n项和为S n，且a n＝2S n－3，则{a n}的通项公式是________．解析：由a n＝2S n－3得a n－1＝2S n－1－3(n≥2)，两式相减得a n－a n－1＝2a n(n≥2)，a n∴a n＝－a n－1(n≥2)，＝－1(n≥2)．a n－1故{a n}是公比为－1的等比数列，令n＝1得a1＝2a1－3，∴a1＝3，故a n＝3·(－1)n－1.答案：a n＝3·(－1)n－16．在等差数列{a n}中，a1＝2，a3＝6，若将a1，a4，a5都加上同一个数，所得的三个数依次成等比数列，则所加的这个数为________．解析：设等差数列{a n}的公差为d，所求的数为m，则Error!∴d＝2，∴a4＝8，a5＝10，∵a1＋m，a4＋m，a5＋m成等比数列，∴(a4＋m)2＝(a1＋m)(a5＋m)，即(8＋m)2＝(2＋m)(10＋m)，解得m＝－11.答案：－117．已知数列{a n}的前n项和S n＝2－a n，求证：数列{a n}是等比数列．证明：∵S n＝2－a n，∴S n＋1＝2－a n＋1.∴a n＋1＝S n＋1－S n＝(2－a n＋1)－(2－a n)＝a n－a n＋1.1∴a n＋1＝a n.2又∵S1＝2－a1，∴a1＝1≠0.1又由a n＋1＝a n知a n≠0，2a n＋1 1∴＝.a n 24∴数列{a n}是等比数列．8．已知数列{a n}是各项为正数的等比数列，且a2＝9，a4＝81.(1)求数列{a n}的通项公式a n；(2)若b n＝log3a n，求证：数列{b n}是等差数列．解：(1)求数列{a n}的公比为q，a4 81∵a2＝9，a4＝81.则q2＝＝＝9，a2 9又∵a n>0，∴q>0，∴q＝3，故通项公式a n＝a2q n－2＝9×3n－2＝3n，n∈N*.(2)证明：由(1) 知a n＝3n，∴b n＝log3a n＝log33n＝n，∴b n＋1－b n＝(n＋1)－n＝1(常数)，n∈N*，故数列{b n}是一个公差等于1的等差数列．5。

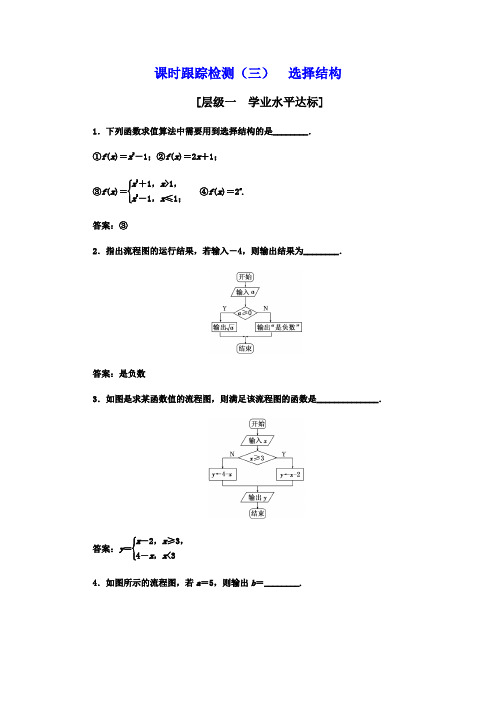
课时跟踪检测（三） 选择结构[层级一 学业水平达标]1．下列函数求值算法中需要用到选择结构的是________． ①f (x )＝x 2－1；②f (x )＝2x ＋1；③f (x )＝⎩⎪⎨⎪⎧x 2＋1，x >1，x 2－1，x ≤1；④f (x )＝2x.答案：③2．指出流程图的运行结果，若输入－4，则输出结果为________．答案：是负数3．如图是求某函数值的流程图，则满足该流程图的函数是______________．答案：y ＝⎩⎪⎨⎪⎧x －2，x ≥3，4－x ，x <34．如图所示的流程图，若a ＝5，则输出b ＝________.解析：这是一个分段函数b ＝⎩⎪⎨⎪⎧a 2＋1，a ≤5，2a ，a ＞5，的求值问题．根据条件易知，b ＝52＋1＝26.答案：265．设计一个判断正整数p 是否是正整数q 的约数的算法，并画出其流程图． 解：算法如下： S1 输入p ，q ；S2 判断p 除q 的余数r 是否为零，如果r ＝0，则输出“p 是q 的约数”；否则，输出“p 不是q 的约数”．流程图：[层级二 应试能力达标]1．如图所示的流程图的功能是________．解析：根据条件结构的定义， 当a ≥b 时，输出a －b ； 当a ＜b 时，输出b －a . 故输出|a －b |. 答案：计算|a －b |2．阅读如图所示的流程图，若运行该程序后输出的y 值为18，则输入的实数x 的值为________．解析：由流程图知：令2x 2－1＝18(x >0)，则x ＝34，令⎝ ⎛⎭⎪⎫12x ＝18(x ≤0)，无解，∴输入的实数x ＝34.答案：343．已知函数y ＝|x －3|，如流程图表示的是给定x 的值，求其相应函数值的算法，请将该流程图补充完整．其中①处应填________，②处应填________．解析：由y ＝|x －3|＝⎩⎪⎨⎪⎧x －3，x ≥3，3－x ，x ＜3.∴①处应填“x ＜3”，②处应填“y ←x －3”． 答案：x ＜3 y ←x －34．阅读如图所示的流程图，若输入值x ＝3，则输出的结果是________．答案：1.55．对任意非零实数a ，b ，若a ⊗b 的运算原理如流程图所示，则3⊗2＝________.解析：由于a ＝3，b ＝2，则a ≤b 不成立， 则输出a ＋1b ＝3＋12＝2. 答案：26．如图，x 1，x 2，x 3为某次考试三个评阅人对同一道题的独立评分，p 为该题的最终得分，当x 1＝6，x 2＝9，p ＝8.5时，x 3等于________．解析：x 1＝6，x 2＝9，|x 1－x 2|＝3≤2不成立，即为“N”， 所以再输入x 3；由绝对值的意义(数轴上一个点到另一个点的距离)和不等式|x 3－x 1|<|x 3－x 2|知， 点x 3到点x 1的距离小于点x 3到x 2的距离，所以当x 3<7.5时，|x 3－x 1|<|x 3－x 2|成立，即为“Y”， 此时x 2＝x 3， 所以p ＝x 1＋x 32，即6＋x 32＝8.5，解得x 3＝11>7.5，不合题意；当x 3≥7.5时，|x 3－x 1|<|x 3－x 2|不成立，即为“N”， 此时x 1＝x 3， 所以p ＝x 3＋x 22，即x 3＋92＝8.5，解得x 3＝8>7.5，符合题意．答案：87．下图的流程图，如果输入三个实数a ，b ，c ，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入__________________．答案：c >x8．给定下面的流程图，要使输出的结果在区间[－1,0]上，则输入的x 的取值范围是__________．解析：此流程图对应函数为y ＝⎩⎪⎨⎪⎧x 2，x <0，4－2x ，x ≥0，若y ∈[－1,0]，则⎩⎪⎨⎪⎧－1≤x 2≤0，x <0或⎩⎪⎨⎪⎧－1≤4－2x ≤0，x ≥0，解得2≤x ≤52.答案：⎣⎢⎡⎦⎥⎤2，52 9.求方程ax 2＋(a ＋1)x ＋1＝0根的算法流程图如图所示，根据流程图，回答下列问题：(1)本题中所给的流程图正确吗？它表示的是哪一个问题的算法流程图？ (2)写出一个正确的算法，并画出流程图．解：(1)本题中给出的流程图不正确．因为它没有体现出对a 的取值的判断，它只解决了算法中的一部分，即a ≠0时的情形，这样是达不到求解的目的．(2)算法如下： S1 输入a ；S2 如果a ＝0，则x ←－1，输出x ， 否则x 1←－1，x 2←－1a，输出x 1，x 2.流程图如图所示．10．已知下列算法： S1 输入x ；S2 若x >0，执行S3，否则执行S4； S3 y ←2x ＋1，转S7；S4 若x ＝0，执行S5，否则执行S6； S5 y ←12，转S7；S6 y ←－x ，转S7； S7 输出y ；S8 结束．(1)指出其功能(用算式表示)； (2)画出该算法的流程图．解：(1)求函数y ＝⎩⎪⎨⎪⎧2x ＋1，x >0，12，x ＝0，－x ，x <0的函数值．(2)流程图如下：。

课时跟踪检测（八） 等差数列的前n 项和层级一 学业水平达标1．已知数列{a n }的通项公式为a n ＝2－3n ，则{a n }的前n 项和S n 等于( ) A ．－32n 2＋n2B ．－32n 2－n2C.32n 2＋n 2D.32n 2－n 2解析：选A ∵a n ＝2－3n ，∴a 1＝2－3＝－1，∴S n ＝n －1＋2－3n2＝－32n 2＋n2.2．若等差数列{a n }的前5项的和S 5＝25，且a 2＝3，则a 7等于( ) A ．12 B ．13 C ．14D ．15解析：选B ∵S 5＝5a 3＝25，∴a 3＝5. ∴d ＝a 3－a 2＝5－3＝2.∴a 7＝a 2＋5d ＝3＋10＝13.故选B.3．设等差数列{a n }的前n 项和为S n ，若S 3＝9，S 6＝36，则a 7＋a 8＋a 9等于( ) A ．63 B ．45 C ．36D ．27 解析：选B ∵a 7＋a 8＋a 9＝S 9－S 6，而由等差数列的性质可知，S 3，S 6－S 3，S 9－S 6构成等差数列，所以S 3＋(S 9－S 6)＝2(S 6－S 3)，即a 7＋a 8＋a 9＝S 9－S 6＝2S 6－3S 3＝2×36－3×9＝45.4．已知等差数列{a n }的前n 项和为S n,7a 5＋5a 9＝0，且a 9>a 5，则S n 取得最小值时n 的值为( )A ．5B ．6C ．7D ．8解析：选B 由7a 5＋5a 9＝0，得a 1d ＝－173.又a 9>a 5，所以d >0，a 1<0.因为函数y ＝d 2x 2＋⎝⎛⎭⎪⎫a 1－d 2x 的图象的对称轴为x ＝12－a 1d ＝12＋173＝376，取最接近的整数6，故S n 取得最小值时n 的值为6.5．设S n 是等差数列{a n }的前n 项和，若a 5a 3＝59，则S 9S 5等于( )A ．1B ．－1C ．2D.12解析：选A S 9S 5＝92a 1＋a 952a 1＋a 5＝9×2a 55×2a 3＝9a 55a 3＝95×59＝1. 6．若等差数列{a n }的前n 项和为S n ＝An 2＋Bn ，则该数列的公差为________．解析：数列{a n }的前n 项和为S n ＝An 2＋Bn ，所以当n ≥2时，a n ＝S n －S n －1＝An 2＋Bn －A (n －1)2－B (n －1)＝2An ＋B －A ，当n ＝1时满足，所以d ＝2A .答案：2A7．设等差数列{a n }的前n 项和为S n ，且S m ＝－2，S m ＋1＝0，S m ＋2＝3，则m ＝________. 解析：因为S n 是等差数列{a n }的前n 项和，所以数列⎩⎨⎧⎭⎬⎫S n n 是等差数列，所以S m m ＋S m ＋2m ＋2＝2S m ＋1m ＋1，即－2m＋3m ＋2＝0，解得m ＝4. 答案：48．设项数为奇数的等差数列，奇数项之和为44，偶数项之和为33，则这个数列的中间项是______，项数是______．解析：设等差数列{a n }的项数为2n ＋1，S 奇＝a 1＋a 3＋…＋a 2n ＋1＝n ＋a 1＋a 2n ＋12＝(n ＋1)a n ＋1，S 偶＝a 2＋a 4＋a 6＋…＋a 2n ＝n a 2＋a 2n2＝na n ＋1，所以S 奇S 偶＝n ＋1n ＝4433，解得n ＝3，所以项数2n ＋1＝7， S 奇－S 偶＝a n ＋1，即a 4＝44－33＝11为所求中间项．答案：11 79．已知数列{a n }的前n 项和为S n ，且满足log 2(S n ＋1)＝n ＋1，求数列{a n }的通项公式． 解：由已知条件，可得S n ＋1＝2n ＋1，则S n ＝2n ＋1－1.当n ＝1时，a 1＝S 1＝3， 当n ≥2时，a n ＝S n －S n －1＝(2n ＋1－1)－(2n －1)＝2n，又当n ＝1时，3≠21，故a n ＝⎩⎪⎨⎪⎧3，n ＝1，2n，n ≥2.10．在等差数列{a n }中，a 10＝18，前5项的和S 5＝－15. (1)求数列{a n }的通项公式；(2)求数列{a n }的前n 项和的最小值，并指出何时取得最小值． 解：(1)设{a n }的首项、公差分别为a 1，d . 则⎩⎪⎨⎪⎧a 1＋9d ＝18，a 1＋2d ＝－3，解得a 1＝－9，d ＝3， ∴a n ＝3n －12. (2)S n ＝n a 1＋a n2＝12(3n 2－21n ) ＝32⎝ ⎛⎭⎪⎫n －722－1478， ∴当n ＝3或4时，前n 项的和取得最小值为－18.层级二 应试能力达标1．已知等差数列{a n }的前n 项和为S n ，S 4＝40，S n ＝210，S n －4＝130，则n ＝( ) A ．12 B ．14 C ．16D ．18解析：选B 因为S n －S n －4＝a n ＋a n －1＋a n －2＋a n －3＝80，S 4＝a 1＋a 2＋a 3＋a 4＝40，所以4(a 1＋a n )＝120，a 1＋a n ＝30，由S n ＝n a 1＋a n2＝210，得n ＝14.2．在等差数列{a n }中，S n 是其前n 项和，且S 2 011＝S 2 014，S k ＝S 2 009，则正整数k 为( ) A ．2 014 B ．2 015 C ．2 016D ．2 017解析：选C 因为等差数列的前n 项和S n 是关于n 的二次函数，所以由二次函数的对称性及S 2 011＝S 2 014，S k ＝S 2 009，可得2 011＋2 0142＝2 009＋k2，解得k ＝2 016.故选C.3．若数列{a n }满足：a 1＝19，a n ＋1＝a n －3(n ∈N ＋)，则数列{a n }的前n 项和数值最大时，n 的值为( )A ．6B ．7C ．8D ．9解析：选B 因为a n ＋1－a n ＝－3，所以数列{a n }是以19为首项，－3为公差的等差数列，所以a n ＝19＋(n －1)×(－3)＝22－3n .设前k 项和最大，则有⎩⎪⎨⎪⎧a k ≥0，a k ＋1≤0，所以⎩⎪⎨⎪⎧22－3k ≥0，22－k ＋，所以193≤k ≤223.因为k ∈N ＋，所以k ＝7. 故满足条件的n 的值为7.4．已知等差数列{a n }和{b n }的前n 项和分别为A n 和B n ，且A n B n ＝7n ＋45n ＋3，则使得a nb n为整数的正整数n 的个数是( )A ．2B ．3C ．4D ．5解析：选 D ∵a nb n ＝a 1＋a 2n －12b 1＋b 2n －12＝a 1＋a 2n －12n －b 1＋b 2n －12n －＝A 2n －1B 2n －1＝n －＋452n －1＋3＝14n ＋382n ＋2＝7＋12n ＋1，∴当n 取1,2,3,5,11时，符合条件，∴符合条件的n 的个数是5. 5．若数列{a n }是等差数列，首项a 1<0，a 203＋a 204>0，a 203·a 204<0，则使前n 项和S n <0的最大自然数n 是________．解析：由a 203＋a 204>0⇒a 1＋a 406>0⇒S 406>0，又由a 1<0且a 203·a 204<0，知a 203<0，a 204>0，所以公差d >0，则数列{a n }的前203项都是负数，那么2a 203＝a 1＋a 405<0，所以S 405<0，所以使前n 项和S n <0的最大自然数n ＝405.答案：4056．在等差数列{a n }中，a 10<0，a 11>0，且a 11>|a 10|，则满足S n <0的n 的最大值为________． 解析：因为a 10<0，a 11>0，且a 11>|a 10|， 所以a 11>－a 10，a 1＋a 20＝a 10＋a 11>0， 所以S 20＝a 1＋a 202>0.又因为a 10＋a 10<0， 所以S 19＝a 10＋a 102＝19a 10<0，故满足S n <0的n 的最大值为19. 答案：197．已知等差数列{a n }的公差d >0，前n 项和为S n ，且a 2a 3＝45，S 4＝28. (1)求数列{a n }的通项公式； (2)若b n ＝S n n ＋c(c 为非零常数)，且数列{b n }也是等差数列，求c 的值．解：(1)∵S 4＝28，∴a 1＋a 42＝28，a 1＋a 4＝14，a 2＋a 3＝14，又a 2a 3＝45，公差d >0， ∴a 2<a 3，∴a 2＝5，a 3＝9，∴⎩⎪⎨⎪⎧a 1＋d ＝5，a 1＋2d ＝9，解得⎩⎪⎨⎪⎧a 1＝1，d ＝4，∴a n ＝4n －3.(2)由(1)，知S n ＝2n 2－n ，∴b n ＝S nn ＋c ＝2n 2－nn ＋c，∴b 1＝11＋c ，b 2＝62＋c ，b 3＝153＋c. 又{b n }也是等差数列， ∴b 1＋b 3＝2b 2，即2×62＋c ＝11＋c ＋153＋c ，解得c ＝－12(c ＝0舍去)．8．在等差数列{a n }中，a 10＝23，a 25＝－22. (1)数列{a n }前多少项和最大？ (2)求{|a n |}的前n 项和S n .解：(1)由⎩⎪⎨⎪⎧a 1＋9d ＝23，a 1＋24d ＝－22，得⎩⎪⎨⎪⎧a 1＝50，d ＝－3，∴a n ＝a 1＋(n －1)d ＝－3n ＋53. 令a n >0，得n <533， ∴当n ≤17，n ∈N ＋时，a n >0； 当n ≥18，n ∈N ＋时，a n <0， ∴{a n }的前17项和最大． (2)当n ≤17，n ∈N ＋时，|a 1|＋|a 2|＋…＋|a n |＝a 1＋a 2＋…＋a n ＝na 1＋n n －2d ＝－32n 2＋1032n . 当n ≥18，n ∈N ＋时， |a 1|＋|a 2|＋…＋|a n |＝a 1＋a 2＋…＋a 17－a 18－a 19－…－a n＝2(a 1＋a 2＋…＋a 17)－(a 1＋a 2＋…＋a n ) ＝2⎝ ⎛⎭⎪⎫－32×172＋1032×17－⎝ ⎛⎭⎪⎫－32n 2＋1032n ＝32n 2－1032n ＋884. ∴S n＝⎩⎪⎨⎪⎧－32n 2＋1032n ，n ≤17，n ∈N ＋，32n 2－1032n ＋884，n ≥18，n ∈N ＋.。

课时跟踪训练(五) 量 词1．下列命题：①有的质数是偶数；②与同一平面所成的角相等的两条直线平行；③有的三角形的三个内角成等差数列；④与圆只有一个公共点的直线是圆的切线，其中是全称命题的是________，是存在性命题的是________．(只填序号)2．下列命题中的假命题是________．①∀x ∈R,2x －1>0； ②∀x ∈N *，(x －1)2>0；③∃x ∈R ，lg x <1；④∃x ∈R ，tan x ＝2.3．用符号“∀”或“∃”表示下面含有量词的命题：(1)实数的平方大于或等于0：________________________________________________；(2)存在一对实数，使3x －2y ＋1≥0成立：_____________________________________.4．命题“∀x ∈R ＋，2x ＋1x＞a 成立”是真命题，则a 的取值范围是________． 5．已知“∀x ∈R ，ax 2＋2ax ＋1>0”为真命题，则实数a 的取值范围是________．6．判断下列命题是全称命题还是存在性命题，并判断其真假：(1)对任意x ∈R ，z x ＞0(z >0)；(2)对任意非零实数x 1，x 2，若x 1＜x 2，则1x 1>1x 2； (3)∃α∈R ，使得sin(α＋π3)＝sin α； (4)∃x ∈R ，使得x 2＋1＝0.7．判断下列命题的真假，并说明理由．(1)∀x∈R，都有x2－x＋1>1 2；(2)∃α，β，使cos(α－β)＝cos α－cos β；(3)∀x，y∈N，都有(x－y)∈N；(4)∃x，y∈Z，使2x＋y＝3.8．(1)对于任意实数x，不等式sin x＋cos x>m恒成立，求实数m的取值范围；(2)存在实数x，不等式sin x＋cos x>m有解，求实数m的取值范围．答案课时跟踪训练(五)1．解析：根据所含量词可知②④是全称命题，①③是存在性命题．答案：②④①③2．解析：对②，x＝1时，(1－1)2＝0，∴②假．答案：②3．(1)∀x ∈R ，x 2≥0(2)∃x ∈R ，y ∈R,3x －2y ＋1≥04．解析：∵x ∈R ＋，∴2x ＋1x ≥22， ∵命题为真，∴a ＜2 2.答案：(－∞，22)5．解析：当a ＝0时，不等式为1>0，对∀x ∈R,1>0成立．当a ≠0时，若∀x ∈R ，ax 2＋2ax ＋1>0，则⎩⎪⎨⎪⎧ a >0，Δ＝4a 2－4a <0，解得0<a <1.综上，a 的取值范围为[0,1)．答案：[0,1)6．解：(1)(2)是全称命题，(3)(4)是存在性命题．(1)∵z x ＞0(z >0)恒成立，∴命题(1)是真命题．(2)存在x 1＝－1，x 2＝1，x 1＜x 2，但1x 1<1x 2， ∴命题(2)是假命题．(3)当α＝π3时，sin(α＋π3)＝sin α成立， ∴命题(3)为真命题．(4)对任意x ∈R ，x 2＋1＞0，∴命题(4)是假命题． 7．解：(1)法一：当x ∈R 时，x 2－x ＋1＝⎝ ⎛⎭⎪⎫x －122＋34≥34>12，所以该命题是真命题． 法二：x 2－x ＋1>12⇔x 2－x ＋12>0，由于Δ＝1－4×12＝－1<0，所以不等式x 2－x ＋1>12的解集是R ，所以该命题是真命题．(2)当α＝π4，β＝π2时，cos(α－β)＝cos ⎝ ⎛⎭⎪⎫π4－π2＝cos ⎝ ⎛⎭⎪⎫－π4＝cos π4＝22，cos α－cos β＝cos π4－cos π2＝22－0＝22，此时cos (α－β)＝cos α－cos β，所以该命题是真命题．(3)当x ＝2，y ＝4时，x －y ＝－2∉N ，所以该命题是假命题．(4)当x ＝0，y ＝3时，2x ＋y ＝3，即∃x ，y ∈Z ，使2x ＋y ＝3，所以该命题是真命题．8．解：(1)令y ＝sin x ＋cos x ，x ∈R .∵y ＝sin x ＋cos x ＝2sin(x ＋π4)≥－ 2. 又∵∀x ∈R ，sin x ＋cos x >m 恒成立．∴只要m <－2即可．∴所求m 的取值范围是(－∞，－2)．(1)令y ＝sin x ＋cos x ，x ∈R .∵y ＝sin x ＋cos x ＝2sin(x ＋π4)∈[－2， 2 ]， 又∵∃x ∈R ，sin x ＋cos x >m 有解．∴只要m <2即可．∴所求m 的取值范围是(－∞，2)．。

课时跟踪检测(二) 数列的函数特性层级一学业水平达标1．下列四个数列中，既是无穷数列又是递增数列的是（）A．1，错误!，错误!,错误!，… B．sin错误!，sin错误!，sin错误!，…C．－1，－错误!，－错误!，－错误!，… D．1，错误!,错误!，…,错误!解析：选C A是递减数列，B是摆动数列，D是有穷数列，故选C.2．已知数列{a n｝的通项公式是a n＝错误!，那么这个数列是( ) A．递增数列B．递减数列C．常数列D．摆动数列解析：选A a n＝错误!＝1－错误!，随着n的增大而增大．3．数列｛a n}中,a n＝－n2＋11n，则此数列最大项的值是( ）A。

错误!B．30C．31 D．32解析：选B a n＝－n2＋11n＝－错误!2＋错误!，∵n∈N＋，∴当n＝5或6时，a n取最大值30,故选B.4．数列｛a n}中，a1＝1,以后各项由公式a1·a2·a3·…·a n＝n2给出，则a3＋a5等于（）A。

错误!B。

错误!C。

错误! D.错误!解析：选C ∵a1·a2·a3·…·a n＝n2，∴a1·a2·a3＝9,a1·a2＝4，∴a3＝错误!。

同理a5＝错误!,∴a3＋a5＝错误!＋错误!＝错误!.5．已知数列｛a n}满足a1〉0，且a n＋1＝错误!a n，则数列{a n}的最大项是( )A．a1B．a9C．a10D．不存在解析：选A ∵a1>0且a n＋1＝错误!a n，∴a n〉0，错误!＝错误!〈1,∴a n＋1〈a n，∴此数列为递减数列，故最大项为a1.6．若数列｛a n}的通项公式为a n＝错误!(k>0，且k为常数），则该数列是________（填“递增”“递减”）数列．解析：错误!＝错误!·错误!＝错误!<1.∵k>0，∴a n〉0，∴a n＋1<a n，∴｛a n}是递减数列．答案：递减7．数列{－2n2＋9n＋3｝中最大项的值为________．解析：由已知a n＝－2n2＋9n＋3＝－2错误!2＋错误!。

课时跟踪检测（八） 等差数列的前n 项和层级一 学业水平达标1．已知数列{a n }的通项公式为a n ＝2－3n ，则{a n }的前n 项和S n 等于( ) A ．－32n 2＋n2B ．－32n 2－n2C.32n 2＋n 2D.32n 2－n 2解析：选A ∵a n ＝2－3n ，∴a 1＝2－3＝－1，∴S n ＝n －1＋2－3n2＝－32n 2＋n2.2．若等差数列{a n }的前5项的和S 5＝25，且a 2＝3，则a 7等于( ) A ．12 B ．13 C ．14D ．15解析：选B ∵S 5＝5a 3＝25，∴a 3＝5. ∴d ＝a 3－a 2＝5－3＝2.∴a 7＝a 2＋5d ＝3＋10＝13.故选B.3．设等差数列{a n }的前n 项和为S n ，若S 3＝9，S 6＝36，则a 7＋a 8＋a 9等于( ) A ．63 B ．45 C ．36D ．27 解析：选B ∵a 7＋a 8＋a 9＝S 9－S 6，而由等差数列的性质可知，S 3，S 6－S 3，S 9－S 6构成等差数列，所以S 3＋(S 9－S 6)＝2(S 6－S 3)，即a 7＋a 8＋a 9＝S 9－S 6＝2S 6－3S 3＝2×36－3×9＝45.4．已知等差数列{a n }的前n 项和为S n,7a 5＋5a 9＝0，且a 9>a 5，则S n 取得最小值时n 的值为( )A ．5B ．6C ．7D ．8解析：选B 由7a 5＋5a 9＝0，得a 1d ＝－173.又a 9>a 5，所以d >0，a 1<0.因为函数y ＝d 2x 2＋⎝⎛⎭⎪⎫a 1－d 2x 的图象的对称轴为x ＝12－a 1d ＝12＋173＝376，取最接近的整数6，故S n 取得最小值时n 的值为6.5．设S n 是等差数列{a n }的前n 项和，若a 5a 3＝59，则S 9S 5等于( )A ．1B ．－1C ．2D.12解析：选A S 9S 5＝92a 1＋a952a 1＋a5＝9×2a 55×2a 3＝9a 55a 3＝95×59＝1. 6．若等差数列{a n }的前n 项和为S n ＝An 2＋Bn ，则该数列的公差为________．解析：数列{a n }的前n 项和为S n ＝An 2＋Bn ，所以当n ≥2时，a n ＝S n －S n －1＝An 2＋Bn －A (n －1)2－B (n －1)＝2An ＋B －A ，当n ＝1时满足，所以d ＝2A .答案：2A7．设等差数列{a n }的前n 项和为S n ，且S m ＝－2，S m ＋1＝0，S m ＋2＝3，则m ＝________. 解析：因为S n 是等差数列{a n }的前n 项和，所以数列⎩⎨⎧⎭⎬⎫S n n 是等差数列，所以S m m ＋S m ＋2m ＋2＝2S m ＋1m ＋1，即－2m ＋3m ＋2＝0，解得m ＝4. 答案：48．设项数为奇数的等差数列，奇数项之和为44，偶数项之和为33，则这个数列的中间项是______，项数是______．解析：设等差数列{a n }的项数为2n ＋1，S 奇＝a 1＋a 3＋…＋a 2n ＋1＝n ＋a 1＋a 2n ＋12＝(n ＋1)a n ＋1，S 偶＝a 2＋a 4＋a 6＋…＋a 2n ＝n a 2＋a 2n2＝na n ＋1，所以S 奇S 偶＝n ＋1n ＝4433，解得n ＝3，所以项数2n ＋1＝7， S 奇－S 偶＝a n ＋1，即a 4＝44－33＝11为所求中间项．答案：11 79．已知数列{a n }的前n 项和为S n ，且满足log 2(S n ＋1)＝n ＋1，求数列{a n }的通项公式． 解：由已知条件，可得S n ＋1＝2n ＋1，则S n ＝2n ＋1－1.当n ＝1时，a 1＝S 1＝3， 当n ≥2时，a n ＝S n －S n －1＝(2n ＋1－1)－(2n －1)＝2n，又当n ＝1时，3≠21，故a n ＝⎩⎪⎨⎪⎧3，n ＝1，2n，n ≥2.10．在等差数列{a n }中，a 10＝18，前5项的和S 5＝－15. (1)求数列{a n }的通项公式；(2)求数列{a n }的前n 项和的最小值，并指出何时取得最小值． 解：(1)设{a n }的首项、公差分别为a 1，d . 则⎩⎪⎨⎪⎧a 1＋9d ＝18，a 1＋2d ＝－3，解得a 1＝－9，d ＝3， ∴a n ＝3n －12. (2)S n ＝n a 1＋a n2＝12(3n 2－21n ) ＝32⎝ ⎛⎭⎪⎫n －722－1478，∴当n ＝3或4时，前n 项的和取得最小值为－18.层级二 应试能力达标1．已知等差数列{a n }的前n 项和为S n ，S 4＝40，S n ＝210，S n －4＝130，则n ＝( ) A ．12 B ．14 C ．16D ．18解析：选B 因为S n －S n －4＝a n ＋a n －1＋a n －2＋a n －3＝80，S 4＝a 1＋a 2＋a 3＋a 4＝40，所以4(a 1＋a n )＝120，a 1＋a n ＝30，由S n ＝n a 1＋a n2＝210，得n ＝14.2．在等差数列{a n }中，S n 是其前n 项和，且S 2 011＝S 2 014，S k ＝S 2 009，则正整数k 为( ) A ．2 014 B ．2 015 C ．2 016D ．2 017解析：选C 因为等差数列的前n 项和S n 是关于n 的二次函数，所以由二次函数的对称性及S 2 011＝S 2 014，S k ＝S 2 009，可得2 011＋2 0142＝2 009＋k2，解得k ＝2 016.故选C.3．若数列{a n }满足：a 1＝19，a n ＋1＝a n －3(n ∈N ＋)，则数列{a n }的前n 项和数值最大时，n 的值为( )A ．6B ．7C ．8D ．9解析：选B 因为a n ＋1－a n ＝－3，所以数列{a n }是以19为首项，－3为公差的等差数列，所以a n ＝19＋(n －1)×(－3)＝22－3n .设前k 项和最大，则有⎩⎪⎨⎪⎧a k ≥0，a k ＋1≤0，所以⎩⎪⎨⎪⎧22－3k ≥0，22－k ＋，所以193≤k ≤223.因为k ∈N ＋，所以k ＝7. 故满足条件的n 的值为7.4．已知等差数列{a n }和{b n }的前n 项和分别为A n 和B n ，且A n B n ＝7n ＋45n ＋3，则使得a nb n为整数的正整数n 的个数是( )A ．2B ．3C ．4D ．5解析：选 D ∵a nb n ＝a 1＋a 2n －12b 1＋b 2n －12＝a 1＋a 2n －12n －b 1＋b 2n －12n －＝A 2n －1B 2n －1＝n －＋452n －1＋3＝14n ＋382n ＋2＝7＋12n ＋1，∴当n 取1,2,3,5,11时，符合条件，∴符合条件的n 的个数是5. 5．若数列{a n }是等差数列，首项a 1<0，a 203＋a 204>0，a 203·a 204<0，则使前n 项和S n <0的最大自然数n 是________．解析：由a 203＋a 204>0⇒a 1＋a 406>0⇒S 406>0，又由a 1<0且a 203·a 204<0，知a 203<0，a 204>0，所以公差d >0，则数列{a n }的前203项都是负数，那么2a 203＝a 1＋a 405<0，所以S 405<0，所以使前n 项和S n <0的最大自然数n ＝405.答案：4056．在等差数列{a n }中，a 10<0，a 11>0，且a 11>|a 10|，则满足S n <0的n 的最大值为________． 解析：因为a 10<0，a 11>0，且a 11>|a 10|， 所以a 11>－a 10，a 1＋a 20＝a 10＋a 11>0， 所以S 20＝a 1＋a 202>0.又因为a 10＋a 10<0， 所以S 19＝a 10＋a 102＝19a 10<0，故满足S n <0的n 的最大值为19. 答案：197．已知等差数列{a n }的公差d >0，前n 项和为S n ，且a 2a 3＝45，S 4＝28. (1)求数列{a n }的通项公式； (2)若b n ＝S nn ＋c(c 为非零常数)，且数列{b n }也是等差数列，求c 的值．解：(1)∵S 4＝28，∴a 1＋a 42＝28，a 1＋a 4＝14，a 2＋a 3＝14，又a 2a 3＝45，公差d >0， ∴a 2<a 3，∴a 2＝5，a 3＝9，∴⎩⎪⎨⎪⎧a 1＋d ＝5，a 1＋2d ＝9，解得⎩⎪⎨⎪⎧a 1＝1，d ＝4，∴a n ＝4n －3.(2)由(1)，知S n ＝2n 2－n ，∴b n ＝S nn ＋c ＝2n 2－nn ＋c，∴b 1＝11＋c ，b 2＝62＋c ，b 3＝153＋c .又{b n }也是等差数列， ∴b 1＋b 3＝2b 2，即2×62＋c ＝11＋c ＋153＋c ，解得c ＝－12(c ＝0舍去)．8．在等差数列{a n }中，a 10＝23，a 25＝－22. (1)数列{a n }前多少项和最大？ (2)求{|a n |}的前n 项和S n .解：(1)由⎩⎪⎨⎪⎧a 1＋9d ＝23，a 1＋24d ＝－22，得⎩⎪⎨⎪⎧a 1＝50，d ＝－3，∴a n ＝a 1＋(n －1)d ＝－3n ＋53. 令a n >0，得n <533，∴当n ≤17，n ∈N ＋时，a n >0； 当n ≥18，n ∈N ＋时，a n <0， ∴{a n }的前17项和最大． (2)当n ≤17，n ∈N ＋时，|a 1|＋|a 2|＋…＋|a n |＝a 1＋a 2＋…＋a n ＝na 1＋n n －2d ＝－32n 2＋1032n . 当n ≥18，n ∈N ＋时， |a 1|＋|a 2|＋…＋|a n |＝a 1＋a 2＋…＋a 17－a 18－a 19－…－a n＝2(a 1＋a 2＋…＋a 17)－(a 1＋a 2＋…＋a n ) ＝2⎝ ⎛⎭⎪⎫－32×172＋1032×17－⎝ ⎛⎭⎪⎫－32n 2＋1032n ＝32n 2－1032n ＋884. ∴S n＝⎩⎪⎨⎪⎧－32n 2＋1032n ，n ≤17，n ∈N ＋，32n 2－1032n ＋884，n ≥18，n ∈N＋.。

2017-2018学年高中数学必修5模块综合检测题2018.1.23本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)⎛⎤112．定义符号函数sgn x ＝⎩⎪⎨⎪⎧0，x ＝0，－1，x ＜0，则当x ∈R 时，不等式x ＋2＞(2x －1)sgn x的解集是( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－3＋334＜x ＜－3＋334 B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＞－3＋334 C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＜－3＋334[Z|X D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－3＋334＜x ＜3第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．若函数f (x )＝(2－a 2)x ＋a 在区间[0,1]上恒为正，则实数a 的取值范围是________． 14．在R 上定义运算⊗，a ⊗b ＝ab ＋2a ＋b ，则满足x ⊗(x －2)<0的实数x 的取值范围为________．必修5模块综合检测题参考答案【第1题解析】由9x 2＋6x ＋1≤0，得(3x ＋1)2≤0，可求得其解为x ＝－31.故选D.【第2题解析】利用线性规划知识，求解目标函数的取值范围．如下图．根据题意得C (1＋，2)．作直线－x ＋y ＝0，并平移，过点B (1,3)和C (1＋，2)时，z ＝－x ＋y 分别取最大值和最小值，则－(1＋)＋2<z <－1＋3，∴z ＝－x ＋y 的取值范围是(1－，2)．故选A.【第5题解析】∵不等式x ＋a x ＋1<2的解集为P ，且1∉P ，∴1＋a 1＋1≥2，即a ＋12a≤0，∴－1<a ≤0.故选D.【第6题解析】∵x >1，y >1，且xy ＝16，∴log 2x >0，log 2y >0且log 2x ＋log 2y ＝log 216＝4.∴log 2x ·log 2y ≤2log2x ＋log2y 2＝4(当且仅当x ＝y ＝4时取等号)．故选D.【第7题解析】由图象知抛物线顶点坐标为(6,11)，且过点(4, 7)．设y ＝a (x －6)2＋11，将点(4,7)代入，得7＝a (4－6)2＋11，∴a ＝－1.∴y ＝－(x －6)2＋11＝－x 2＋12x －25.∴年平均利润为x y ＝－x －x 25＋12＝12－x 25.∵x ＋x 25≥10，即x ＝5时，取等号25，∴当x ＝5时，x y有最大值2.故选C.【第8题解析】∵不等式x 2＋ax ＋1≥0对一切x ∈21成立，∴对一切x ∈21，ax ≥－x 2－1，即a ≥－x x2＋1成立．令g (x )＝－x x2＋1＝－x 1.易知g (x )＝－x 1在21内为增函数．∴当x ＝21时，g (x )max ＝－25.∴a 的取值范围是a ≥－25，即a 的最小值是－25.故选C.【第9题解析】“求(1－a i x )2<1(i ＝1,2,3)都成立的x 的取值范围”实质上是求不等式组2<12<1的解集，由于这几个不等式结构一样，则其中解集“最小”的一个不等式的解集即是不等式组的解集．(1－a i x )2<1即a i 2x2－2a i x <0，a i x (a i x －2)<0.∵a i >0，∴这个不等式可化为x ai 2<0，∴0<x <ai 2.若ai 2取最小值，则a i 应取最大值，因此0<x <a12，故选B.【第11题解析】设租用A 型车x 辆，B 型车y 辆，目标函数为z ＝1 600x ＋2 400y ，则约束条件为x ，y ∈N ，y －x≤7，作出可行域，如图中阴影部分所示，可知目标函数过点P (5,12)时，有最小值z min ＝36 800(元)．故选C.【第12题解析】当x ＞0时，不等式化为x ＋2＞2x －1，解得x ＜3，即0＜x ＜3；当x ＝0时，不等式恒成立；当x ＜0时，不等式化为x ＋2＞(2x －1)－1，即2x 2＋3x －3＜0，解得－433＜x＜433，即－433＜x ＜0.综上可知，不等式的解集为＜x ＜333.故选D.【第13题解析】当2－a 2＝0时，a ＝±.由题意知a ＝时符合题意． 当2－a 2≠0，即a ≠±时，f (x )是一次函数，在[0,1]上是单调的，∴>0，0>0，即－a2＋a ＋2>0.a>0，解得0<a <2且a ≠±.综上可知0<a <2.故填(0,2).【第14题解析】∵x ⊗(x －2)＝x ·(x －2)＋2x ＋x －2＝x 2＋x －2，∴x ⊗(x －2)<0，即x 2＋x －2<0，即(x ＋2)(x －1)<0，∴实数x 的取值范围为－2<x <1.故填(－2,1).【第15题解析】设f (x )＝x 2＋ax ＋2b ，由题意可知f (x )的图象如图1所示，则有>0<0，⇔a ＋b ＋2>0.a ＋2b ＋1<0，图1图2【第16题解析】作出可行域如图所示的阴影部分，平移直线l ：ax ＋by ＝0，由于a >0，b >0，∴直线l 的斜率为－b a<0，∴当直线l 经过点A 时，z ＝ax ＋by 取得最大值6.由x －y ＋2＝0，3x －y －6＝0，解得y ＝6，x ＝4，∴A (4,6)．∴4a ＋6b ＝6.∴32a ＋b ＝1且a >0，b >0.∴a 1＋b 2＝b 2a ＋b 2＝38＋a b ＋3b 4a ≥38＋23b 4a ＝33.(当且仅当a b ＝3b 4a ，即a ＝23b 时取等号)故填33.【第17题答案】y min ＝3.【第17题解析】令t ＝x 2＋1，则t ≥1，且x 2＝t －1.∴y ＝x2＋1x4＋3x2＋3＝t t －1＋3＝t t2＋t ＋1＝t ＋t 1＋1.∵t ≥1，∴t ＋t 1≥2t 1＝2，当且仅当t ＝t 1，即t ＝1时，等号成立．∴当t ＝1时，t 1min ＝2，此时x ＝0，y min ＝t ＋t 1＋1＝3.故当x ＝0时，函数y 取最小值，y min ＝3.【第18题答案】x >2或x <－1m ∈，31，问题转化为g (m )在m ∈，31上恒大于0，则>0，>0，解得x >2或x <－1.故填x >2或x <－1.【第19题答案】23【第19题解析】(1)若a ＝2，则不等式f (x )≥0化为2x 2－5x ＋3≥0，∴不等式f (x )≥0的解集为或x≤13. (2)∵ax 2－(2a ＋1)x ＋a ＋1＝a (x －1)2－(x －1)，令g (a )＝a (x －1)2－(x －1)，则g (a )是关于a 的一次函数，且一次项的系数为(x －1)2≥0，∴当x －1＝0时，f (x )＝0不合题意；当x ≠1时，g (a )为[－2,2]上的增函数．∵f (x )<0恒成立，∴只要使g (a )的最大值g (2)<0即可，即g (2)＝2(x －1)2－(x －1)<0，解得1<x <23. 综上，x 的取值范围是23. 学科*网【第20题答案】（1）f (x )＝38－x ＋10180－5x，x ∈[0,100]；（2）分别用20万元和80万元资金投资A ，B 两种金融产品，可以使公司获得最大利润，最大利润为28万元．【第21题答案】存在常数a ＝41，b ＝21，c ＝41满足题意．【第21题解析】由f (－1)＝0，得a －b ＋c ＝0.①又对x ∈R ，不等式x ≤f (x )≤21(x 2＋1)成立，取x ＝1，有1≤f (1)≤1，∴f (1)＝1，故a ＋b ＋c ＝1.②由①②可得b ＝21，c ＝21－a ，将其代入x ≤f (x )≤21(x 2＋1)，得x ≤ax 2＋21x ＋21－a ≤21(x 2＋1)对x ∈R 恒成立，即x －a≤0 ④1对x ∈R 恒成立．由③得Δ≤0a>0，⇒a ＝41.由④得Δ≤0<0，⇒a ＝41.综合可知，存在常数a ＝41，b ＝21，c ＝41满足题意．【第22题答案】存在实数k ∈[3，＋∞)使不等式恒成立．【第22题解析】存在．将不等式4－kx －x 4≤0变形，即－x 4≤kx －4(x >0)．可设f 1(x )＝－x 4，f 2(x )＝kx －4.故f 2(x )中参数k 的几何意义是直线y ＝kx －4的斜率．由下图知当直线y ＝kx －4与曲线y ＝－x 4相切时，关于x 的方程－x 4＝kx －4有唯一大于0的解，将方程整理成关于x 的一元二次方程kx 2－4x ＋4＝0.由Δ＝(－4)2－4×4×k ＝0，可得k ＝3.又直线y ＝kx －4过定点(0，－4)，故要使f 1(x )≤f 2(x )(x >0)恒成立，只需k ≥3即可．综上，存在实数k ∈[3，＋∞)使不等式恒成立．。

课时跟踪检测（五）数列的递推公式（选学）层级一学业水平达标1．已知数列｛a n｝的首项为a1＝1，且满足a n＋1＝错误!a n＋错误!,则此数列的第4项是（)A．1 B。

错误!C.错误!D.错误!解析：选B 由a1＝1，∴a2＝错误!a1＋错误!＝1，依此类推a4＝错误!。

2．在递减数列｛a n｝中，a n＝kn(k为常数)，则实数k的取值范围是( ）A．R B．（0，＋∞)C．（－∞，0) D．（－∞，0］解析：选C ∵｛a n}是递减数列,∴a n＋1－a n＝k（n＋1)－kn＝k<0.3．数列{a n｝中，a1＝1，对所有的n≥2，都有a1·a2·a3·…·a n ＝n2，则a3＋a5等于( ）A。

错误!B。

错误! C.错误! D.错误!解析：选C 由题意a1a2a3＝32,a1a2＝22,a1a2a3a4a5＝52，a1a2a3a4＝42，则a3＝错误!＝错误!，a5＝错误!＝错误!。

故a3＋a5＝错误!。

4．已知数列｛a n}满足要求a1＝1，a n＋1＝2a n＋1，则a5等于（) A．15 B．16C．31 D．32解析：选C ∵数列｛a n}满足a1＝1，a n＋1＝2a n＋1，∴a2＝2×1＋1＝3，a3＝2×3＋1＝7，a4＝2×7＋1＝15,a5＝2×15＋1＝31。

5．由1,3,5，…，2n－1，…构成数列{a n｝，数列｛b n｝满足b1＝2，当n≥2时,b n＝a b n－1，则b6的值是( ）A．9 B．17C．33 D．65解析：选C ∵b n＝a错误!,∴b2＝a错误!＝a2＝3，b3＝a错误!＝a3＝5，b4＝a错误!＝a5＝9，b5＝a错误!＝a9＝17，b6＝a错误!＝a17＝33。

6．已知数列｛a n｝满足a1＝23,a n＋1＝错误!a n，得a n＝________。

模块综合检测(时间120分钟，满分160分)一、填空题(本大题共14小题，每小题5分，共70分．将答案填在题中的横线上) 1．函数f (x )＝lg(x 2－2x －3)的定义域为________． 解析：由x 2－2x －3>0得x <－1或x >3. 答案：(－∞，－1)∪(3，＋∞)2．在△ABC 中，a ，b ，c 所对的角分别为A ，B ，C ，若a ＝2，A ＝π4，B ＝5π12，则b ＝________.解析：由正弦定理a sin A ＝b sin B得， b ＝a sin B sin A ＝2×6＋2422＝3＋1. 答案：3＋13．已知等比数列{a n }，a 4＝7，a 6＝21，则a 10＝________. 解析：∵a 4＝a 1q 3，a 6＝a 1q 5， ∴q 2＝a 6a 4＝3.∴a 10＝a 6q 4＝189. 答案：1894．已知不等式x 2－2x ＋k 2－1>0对一切实数x 恒成立，则实数k 的取值范围是________． 解析：由题意知Δ＝(－2)2－4(k 2－1)<0，即k 2－2>0，所以k ∈(－∞，－2)∪(2，＋∞)．答案：(－∞，－2)∪(2，＋∞)5．函数y ＝log 2⎝⎛⎭⎫x ＋1x －1＋5(x >1)的最小值为________．解析：∵x >1，∴x ＋1x －1＋5＝x －1＋1x －1＋6≥2(x －1)·1x －1＋6＝8.当且仅当x －1＝1x －1即x ＝2时取等号． ∴y ＝log 2⎝⎛⎭⎫x ＋1x －1＋5≥log 28＝3.∴y ＝log 2⎝⎛⎭⎫x ＋1x －1＋5(x >1)的最小值为3.答案：36．等差数列{a n }的前n 项和为S n ，若S 10＝0，S 15＝25，则S n ＝________.解析：由题意知⎩⎨⎧10a 1＋10×9d 2＝0，15a 1＋15×14d2＝25，解得d ＝23，a 1＝－3，所以S n ＝－3n ＋n (n －1)2×23＝n 2－10n3.答案：n 2－10n37．在平面直角坐标系xOy 中，M 为不等式组⎩⎪⎨⎪⎧2x －y －2≥0，x ＋2y －1≥0，3x ＋y －8≤0所表示的区域上一动点，则直线OM 斜率的最小值为________．解析：已知的不等式组表示的平面区域如图中阴影所示，显然当点M 与点A 重合时直线OM 的斜率最小，由直线方程x ＋2y －1＝0和3x ＋y －8＝0，解得A (3，－1)，故OM 斜率的最小值为－13.答案：－138．已知各项不为0的等差数列{a n }满足a 4－2a 27＋3a 8＝0，数列{b n }是等比数列，且b 7＝a 7，则b 2b 8b 11＝________.解析：设等差数列的公差为d ，由a 4－2a 27＋3a 8＝0，得a 7－3d －2a 27＋3(a 7＋d )＝0，从而有a 7＝2或a 7＝0(a 7＝b 7，而{b n }是等比数列，故舍去)．设{b n }的公比为q ，则b 7＝a 7＝2，所以b 2b 8b 11＝b 7q5·b 7q ·b 7q 4＝(b 7)3＝23＝8.答案：89．在数列{a n }中，已知a 1＝2，a 2＝7，a n ＋2等于a n a n ＋1(n ∈N *)的个位数，则a 2 016的值是________．解析：a 1a 2＝2×7＝14，所以a 3＝4,7×4＝28，所以a 4＝8,4×8＝32，所以a 5＝2,8×2＝16，所以a 6＝6，a 7＝2，a 8＝2，a 9＝4，a 10＝8，a 11＝2，所以从第三项起，{a n }成周期数列，周期数为6,2 016＝336×6，所以a 2 016＝a 6＝6.10．若△ABC 的内角A ，B ，C 满足6sin A ＝4sin B ＝3sin C ，则cos B ＝________. 解析：依题意，结合正弦定理得6a ＝4b ＝3c ，设3c ＝12k (k >0)，则有a ＝2k ，b ＝3k ，c ＝4k ；由余弦定理得cos B ＝a 2＋c 2－b 22ac ＝(2k )2＋(4k )2－(3k )22×2k ×4k＝1116.答案：111611．张晓华同学骑电动自行车以24 km/h 的速度沿着正北方向的公路行驶，在点A 处望见电视塔S 在电动车的北偏东30°方向上，15 min 后到点B 处望见电视塔在电动车的北偏东75°方向上，则电动车在点B 时与电视塔S 的距离是________ km.解析：如图，由条件知AB ＝24×1560＝6.在△ABS 中，∠BAS ＝30°，AB ＝6，∠ABS ＝180°－75°＝105°，所以∠ASB ＝45°.由正弦定理知BS sin 30°＝ABsin 45°，所以BS ＝ABsin 45°sin 30°＝3 2.即电动车在点B 时与电视塔S 的距离是3 2 km. 答案：3 212．若正数x ，y 满足x 2＋3xy －1＝0，则x ＋y 的最小值是________． 解析：对于x 2＋3xy －1＝0可得y ＝13⎝⎛⎭⎫1x －x ， 即x ＋y ＝2x 3＋13x≥22x 3·13x ＝223，当且仅当x ＝22时取等号． 答案：22313．已知二次函数f (x )＝ax 2－x ＋c (x ∈R)的值域为[0，＋∞)，则c ＋2a ＋a ＋2c 的最小值为________．解析：∵二次函数f (x )＝ax 2－x ＋c (x ∈R)的值域[0，＋∞)， ∴a >0，且4ac －14a＝0. ∴ac ＝14，∴c >0.∴c ＋2a ＋a ＋2c ＝c a ＋a c ＋2a ＋2c ≥2c a ·a c ＋24ac ＝2＋8＝10，当且仅当a ＝c 时取等号．14．已知{a n }是首项为1的等比数列，S n 是{a n }的前n 项和，且9S 3＝S 6，则数列⎩⎨⎧⎭⎬⎫1a n 的前5项和为________．解析：设等比数列{a n }的公比为q ，∴9S 3＝S 6. ∴8(a 1＋a 2＋a 3)＝a 4＋a 5＋a 6. ∴a 4＋a 5＋a 6a 1＋a 2＋a 3＝q 3＝8.∴q ＝2，∴a n ＝2n －1. ∴1a n ＝⎝⎛⎭⎫12n －1. ∴数列⎩⎨⎧⎭⎬⎫1a n 是首项为1，公比为12的等比数列，故数列⎩⎨⎧⎭⎬⎫1a n 的前5项和为1×⎣⎡⎦⎤1－⎝⎛⎭⎫1251－12＝3116.答案：3116二、解答题(本大题共6小题，共90分，解答应写出文字说明、证明过程或演算步骤) 15．(本小题满分14分)求不等式12x 2－ax >a 2(a ∈R)的解集． 解：原不等式可化为(3x －a )(4x ＋a )>0.当a >0时，不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪ x <－a 4或x >a 3； 当a ＝0时，不等式的解集为{x |x ∈R 且x ≠0}；当a <0时，不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x <a 3或x >－a 4. 16．(本小题满分14分)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知a ＝b cos C ＋c sin B .(1)求B ；(2)若b ＝2，求△ABC 面积的最大值．解：(1)由已知及正弦定理得sin A ＝sin B cos C ＋sin C sin B ． ① 又A ＝π－(B ＋C )，故sin A ＝sin(B ＋C )＝sin B cos C ＋cos B sin C ． ② 由①②和C ∈(0，π)得sin B ＝cos B . 又B ∈(0，π)，所以B ＝π4.(2)△ABC 的面积S ＝12ac sin B ＝24ac .由已知及余弦定理得4＝a 2＋c 2－2ac cos π4.又a 2＋c 2≥2ac ，故ac ≤42－2，当且仅当a ＝c 时，等号成立． 因此△ABC 面积的最大值为2＋1.17．(本小题满分14分)某企业准备投入适当的广告费对产品进行促销，在一年内预计销售量Q (万件)与广告费x (万元)之间的函数关系为Q ＝3x ＋1x ＋1(x ≥0)．已知生产此产品的年固定投入为3万元，每生产1万元此产品仍需再投入32万元，若每件销售价为“年平均每件生产成本的150%”与“年平均每件所占广告费的50%”之和．(1)试将年利润W (万元)表示为年广告费x (万元)的函数；(2)当年广告费投入多少万元时，企业年利润最大？最大利润为多少？解：(1)由题意可得，产品的生产成本为(32Q ＋3)万元，每万件销售价为32Q ＋3Q ×150%＋xQ×50%万元， 所以年销售收入为⎝⎛⎭⎫32Q ＋3Q ×150%＋xQ ×50%·Q ＝32(32Q ＋3)＋12x 万元， 所以年利润W ＝32(32Q ＋3)＋12x －(32Q ＋3)－x ＝12(32Q ＋3－x )＝－x 2＋98x ＋352(x ＋1)(x ≥0)．(2)令x ＋1＝t (t ≥1)，则W ＝－(t －1)2＋98(t －1)＋352t ＝50－⎝⎛⎭⎫t 2＋32t . 因为t ≥1，所以t 2＋32t ≥2t 2·32t＝8，即W ≤42， 当且仅当t 2＝32t ，即t ＝8时，W 有最大值42，此时x ＝7.答：当年广告费为7万元时，企业年利润最大，最大值为42万元．18．(本小题满分16分)已知公差不为0的等差数列{a n }的首项a 1为a (a ∈R)，且1a 1，1a 2，1a 4成等比数列． (1)求数列{a n }的通项公式；(2)对n ∈N *，试比较1a 2＋1a 22＋1a 23＋…＋1a 2n 与1a 1的大小．解：(1)设等差数列{a n }的公差为d ， 由题意可知⎝⎛⎭⎫1a 22＝1a 1·1a 4， 即(a 1＋d )2＝a 1(a 1＋3d )，从而a 1d ＝d 2. 因为d ≠0.所以d ＝a 1＝a . 故通项公式a n ＝na .(2)记T n ＝1a 2＋1a 22＋…＋1a 2n ，因为a 2n ＝2n a ，所以T n ＝1a ⎝⎛⎭⎫12＋122＋…＋12n ＝1a ·12⎣⎡⎦⎤1－⎝⎛⎭⎫12n 1－12＝1a ⎣⎡⎦⎤1－⎝⎛⎭⎫12n . 从而，当a ＞0时，T n ＜1a 1；当a ＜0时，T n ＞1a 1.19．(本小题满分16分)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，且满足a ＝2sin A ，cos B cos C ＋2a c ＋bc＝0.(1)求c 的值；(2)求△ABC 面积的最大值． 解：(1)∵cos B cos C ＋2a c ＋bc＝0， ∴c cos B ＋2a cos C ＋b cos C ＝0，∴sin C cos B ＋sin B cos C ＋2sin A cos C ＝0， ∴sin A ＋2sin A cos C ＝0.又∵sin A ≠0， ∴cos C ＝－12，∴C ＝2π3，∴c ＝a sin A·sin C ＝ 3.(2)∵cos C ＝－12＝a 2＋b 2－32ab，∴a 2＋b 2＋ab ＝3，∴3ab ≤3，即ab ≤1，当且仅当a ＝b ＝1时取等号， ∴S △ABC ＝12ab sin C ≤34，即△ABC 面积的最大值为34. 20．(本小题满分16分)在△ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，a 2－c 2＝b 2－8bc5，a ＝3，△ABC 的面积为6，D 为△ABC 内(不包括三角形的边)任一点，点D 到三边距离之和为d .(1)求角A 的正弦值； (2)求边b ，c; (3)求d 的取值范围．解：(1)a 2－c 2＝b 2－8bc 5⇒b 2＋c 2－a 22bc ＝45⇒cos A ＝45⇒sin A ＝35.(2)∵S △ABC ＝12bc sin A ＝6.∴bc ＝20.由b 2＋c 2－a 22bc ＝45及bc ＝20与a ＝3解得b ＝4，c ＝5或b ＝5，c ＝4.(3)设点D 到三边的距离分别为x ，y ，z ， 则S △ABC ＝12(3x ＋4y ＋5z )＝6，d ＝x ＋y ＋z＝125＋15(2x ＋y )， 又x ，y 满足⎩⎪⎨⎪⎧3x ＋4y <12，x >0，y >0，画出不等式表示的平面区域得125<d <4.。

课时跟踪检测（六） 等差数列的概念及通项公式层级一 学业水平达标1．已知等差数列{a n }的通项公式为a n ＝3－2n ，则它的公差为( ) A ．2 B ．3 C ．－2D ．－3解析：选C ∵a n ＝3－2n ＝1＋(n －1)×(－2)，∴d ＝－2，故选C. 2．若等差数列{a n }中，已知a 1＝13，a 2＋a 5＝4，a n ＝35，则n ＝( )A ．50B ．51C ．52D ．53解析：选D 依题意，a 2＋a 5＝a 1＋d ＋a 1＋4d ＝4，代入a 1＝13，得d ＝23.所以a n ＝a 1＋(n －1)d ＝13＋(n －1)×23＝23n －13，令a n ＝35，解得n ＝53.3．设x 是a 与b 的等差中项，x 2是a 2与－b 2的等差中项，则a ，b 的关系是( ) A ．a ＝－b B ．a ＝3b C ．a ＝－b 或a ＝3bD ．a ＝b ＝0解析：选C 由等差中项的定义知：x ＝a ＋b2，x 2＝a 2－b 22，∴a 2－b 22＝⎝⎛⎭⎪⎫a ＋b 22，即a 2－2ab －3b 2＝0. 故a ＝－b 或a ＝3b .4．数列{a n }中，a 1＝2,2a n ＋1＝2a n ＋1，则a 2 015的值是( ) A ．1 006 B ．1 007 C ．1 008D ．1 009解析：选D 由2a n ＋1＝2a n ＋1，得a n ＋1－a n ＝12，所以{a n }是等差数列，首项a 1＝2，公差d＝12， 所以a n ＝2＋12(n －1)＝n ＋32，所以a 2 015＝2 015＋32＝1 009.5．已知数列3,9,15，…，3(2n －1)，…，那么81是数列的( ) A ．第12项 B ．第13项 C ．第14项D ．第15项解析：选C a n ＝3(2n －1)＝6n －3，由6n －3＝81，得n ＝14. 6．在等差数列{a n }中，a 3＝7，a 5＝a 2＋6，则a 6＝________. 解析：设等差数列{a n }的公差为d ，由题意，得⎩⎪⎨⎪⎧a 1＋2d ＝7，a 1＋4d ＝a 1＋d ＋6.解得⎩⎪⎨⎪⎧a 1＝3，d ＝2.∴a n ＝a 1＋(n －1)d ＝3＋(n －1)×2＝2n ＋1. ∴a 6＝2×6＋1＝13. 答案：137．已知数列{a n }中，a 1＝3，a n ＝a n －1＋3(n ≥2)，则a n ＝________. 解析：因为n ≥2时，a n －a n －1＝3，所以{a n }是以a 1＝3为首项，公差d ＝3的等差数列．所以a n ＝a 1＋(n －1)d ＝3＋3(n －1)＝3n .答案：3n8．已知{a n }为等差数列，且a 7－2a 4＝－1，a 3＝0，则公差d ＝________. 解析：根据题意得：a 7－2a 4＝a 1＋6d －2(a 1＋3d )＝－a 1＝－1，∴a 1＝1.又a 3＝a 1＋2d ＝1＋2d ＝0， ∴d ＝－12.答案：－129．已知数列{a n }满足a 1＝2，a n ＋1＝2a na n ＋2，则数列⎩⎨⎧⎭⎬⎫1a n 是否为等差数列？说明理由． 解：数列⎩⎨⎧⎭⎬⎫1a n 是等差数列，理由如下：因为a 1＝2，a n ＋1＝2a na n ＋2， 所以1a n ＋1＝a n ＋22a n ＝12＋1a n，所以1a n ＋1－1a n ＝12(常数)． 所以⎩⎨⎧⎭⎬⎫1a n 是以1a 1＝12为首项，公差为12的等差数列．10．若1b ＋c ，1a ＋c ，1a ＋b是等差数列，求证：a 2，b 2，c 2成等差数列． 证明：由已知得1b ＋c ＋1a ＋b ＝2a ＋c ，通分有2b ＋a ＋c b ＋c a ＋b ＝2a ＋c. 进一步变形有2(b ＋c )(a ＋b )＝(2b ＋a ＋c )(a ＋c )，整理，得a 2＋c 2＝2b 2， 所以a 2，b 2，c 2成等差数列．层级二 应试能力达标1．若数列{a n }为等差数列，a p ＝q ，a q ＝p (p ≠q )，则a p ＋q 为( ) A ．p ＋q B ．0 C ．－(p ＋q )D.p ＋q2解析：选B ∵a p ＝a 1＋(p －1)d ，a q ＝a 1＋(q －1)d ，∴⎩⎪⎨⎪⎧a 1＋p －d ＝q ， ①a 1＋q －d ＝p . ②①－②，得(p －q )d ＝q －p . ∵p ≠q ，∴d ＝－1.代入①，有a 1＋(p －1)×(－1)＝q ，∴a 1＝p ＋q －1. ∴a p ＋q ＝a 1＋(p ＋q －1)d ＝p ＋q －1＋(p ＋q －1)×(－1)＝0.2．已知x ≠y ，且两个数列x ，a 1，a 2，…，a m ，y 与x ，b 1，b 2，…，b n ，y 各自都成等差数列，则a 2－a 1b 2－b 1等于( ) A.m n B.m ＋1n ＋1 C.n mD.n ＋1m ＋1解析：选D 设这两个等差数列公差分别是d 1，d 2，则a 2－a 1＝d 1，b 2－b 1＝d 2.第一个数列共(m ＋2)项，∴d 1＝y －x m ＋1；第二个数列共(n ＋2)项，∴d 2＝y －x n ＋1.这样可求出a 2－a 1b 2－b 1＝d 1d 2＝n ＋1m ＋1. 3．已知数列{a n }，对任意的n ∈N ＋，点P n (n ，a n )都在直线y ＝2x ＋1上，则{a n }为( ) A ．公差为2的等差数列 B ．公差为1的等差数列 C ．公差为－2的等差数列D ．非等差数列解析：选A 由题意知a n ＝2n ＋1，∴a n ＋1－a n ＝2，应选A.4．如果a 1，a 2，…，a 8为各项都大于零的等差数列，且公差d ≠0，则( ) A ．a 3a 6>a 4a 5 B ．a 3a 6<a 4a 5 C ．a 3＋a 6>a 4＋a 5D ．a 3a 6＝a 4a 5解析：选B 由通项公式，得a 3＝a 1＋2d ，a 6＝a 1＋5d ，那么a 3＋a 6＝2a 1＋7d ，a 3a 6＝(a 1＋2d )(a 1＋5d )＝a 21＋7a 1d ＋10d 2，同理a 4＋a 5＝2a 1＋7d ，a 4a 5＝a 21＋7a 1d ＋12d 2，显然a 3a 6－a 4a 5＝－2d 2<0，故选B.5．数列{a n }是首项为2，公差为3的等差数列，数列{b n }是首项为－2，公差为4的等差数列．若a n ＝b n ，则n 的值为________．解析：a n ＝2＋(n －1)×3＝3n －1，b n ＝－2＋(n －1)×4＝4n －6，令a n ＝b n ，得3n －1＝4n －6，∴n ＝5. 答案：56．在数列{a n }中，a 1＝3，且对于任意大于1的正整数n ，点(a n ， a n －1)都在直线x －y －3＝0上，则a n ＝________.解析：由题意得a n －a n －1＝3，所以数列{a n }是首项为3，公差为3的等差数列，所以a n ＝3n ，a n ＝3n 2.答案：3n 27．已知数列{a n }满足a 1＝1，且a n ＝2a n －1＋2n(n ≥2，且∈N ＋)． (1)求a 2，a 3；(2)证明：数列⎩⎨⎧⎭⎬⎫a n 2n 是等差数列；(3)求数列{a n }的通项公式a n .解：(1)a 2＝2a 1＋22＝6，a 3＝2a 2＋23＝20. (2)证明：∵a n ＝2a n －1＋2n(n ≥2，且n ∈N ＋)， ∴a n 2n ＝a n －12n －1＋1(n ≥2，且n ∈N ＋)， 即a n 2n －a n －12n －1＝1(n ≥2，且n ∈N ＋)， ∴数列⎩⎨⎧⎭⎬⎫a n 2n 是首项为a 121＝12，公差d ＝1的等差数列．(3)由(2)，得a n 2n ＝12＋(n －1)×1＝n －12，∴a n ＝⎝ ⎛⎭⎪⎫n －12·2n.8．数列{a n }满足a 1＝2，a n ＋1＝(λ－3)a n ＋2n(n ∈N ＋)． (1)当a 2＝－1时，求λ及a 3的值；(2)是否存在λ的值，使数列{a n }为等差数列？若存在求其通项公式；若不存在说明理由． 解：(1)∵a 1＝2，a 2＝－1，a 2＝(λ－3)a 1＋2，∴λ＝32.∴a 3＝－32a 2＋22，∴a 3＝112.(2)∵a 1＝2，a n ＋1＝(λ－3)a n ＋2n， ∴a 2＝(λ－3)a 1＋2＝2λ－4.a 3＝(λ－3)a 2＋4＝2λ2－10λ＋16.若数列{a n }为等差数列，则a 1＋a 3＝2a 2. 即λ2－7λ＋13＝0.∵Δ＝49－4×13<0，∴方程无实数解．∴λ值不存在．∴不存在λ的值使{a n }成等差数列．。