工艺定位误差的分析与计算

定位误差分析计算综合实例定位误差的分析与计算，在夹具设计中占有重要的地位，定位误差的大小是定位方案可否确信的重要依据。

为了把握定位误差计算的相关知识，本末节将给出一些计算实例，抛砖引玉，以使学习者取得触类旁通、融会贯通的学习成效。

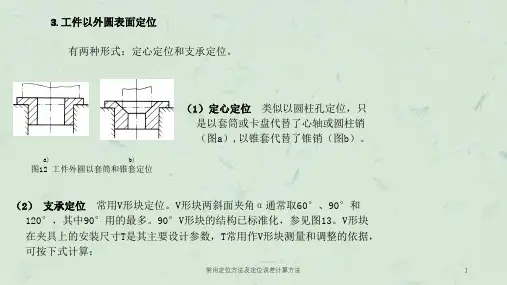
例3-3 如图3.25所示，工件以底面定位加工孔内键槽，求尺寸h 的定位误差？解：（1）基准不重合误差求jb ∆ 设计基准为孔的下母线，定位基准为底平面，阻碍二者的因素有尺寸h 和h 1，故jb ∆由两部份组成：φD 半径的转变产生2D ∆尺寸h 1转变产生12h T ，因此122h jb T D+∆=∆ 底平面，对刀基准为（2）基准位置误差jw ∆ 定位基准为工件与定位基准接触的支承板的工作表面，不记形状误差，那么有0=∆jw因此槽底尺寸h 的定位误差为 122h dw T D+∆=∆ 例3-4 有一批直径为0d T d -φ的工件如图3.27所示。

外圆已加工合格，今用V形块定位铣宽度为b 的槽。

假设要求保证槽底尺寸别离为1L 、2L 和3L 。

试别离分析计算这三种不同尺寸要求的定位误差。

解：（1）第一计算V 形块定位外圆时的基准位置误差jw ∆在图3.26中，对刀基准是一批工件平均轴线所处的位置O 点，设定位基准为外圆的轴线，加工精度参数的方向与21O O 相同，那么基准位置误差jw ∆为图中O 1点到O 2点的距离。

在ΔO 1CO 2中，22212α=∠=O CO T CO d ，，依照勾股定理求得 221sin 2αd jw T O O E ==∆=∆（2）别离计算图3.27三种情形的定位误差①图a ）中1L 尺寸的定位误差2)(2sin 2sin 201ααd L dw djw jb T T E B =∆=∆=∆=∆=∆②图b ）中2L 尺寸的定位误差L 2L 3L 10dTd -φ b图3.27 V 形块定位外圆时定位误差的计算图3.25 内键槽槽底尺寸定位误差计算图3.26 V 形块定位外圆时基准位置误差jw ∆的计算1—最大直径 2—平均直径3—最小直径BA α/ 21 C 32 O OO2sin 22αd jw d jb T E T B =∆=∆=∆=∆需要说明的是2L 尺寸定位误差dw ∆的合成问题。

P.157（题3-3）习题（定位误差分析计算）解答：答：本工序铣槽要保证两个加工精度：尺寸014.054-和对称度不大于0.03。

1、采用第一种定位方案（见b 图）时，（1）对于尺寸014.054-的定位误差： )047.0(314.0021.0145sin 121.012sin 12=≤≈⎪⎭⎫ ⎝⎛-︒=⎪⎪⎪⎪⎭⎫ ⎝⎛-=∆-∆=∆αd JB JW DW T 所以能保证尺寸014.054-的加工精度要求。

（2）对于对称度的定位误差：000=+=∆+∆=∆JW JB DW（注：由于V 形块对工件外圆定位时，其定位基准就是过外圆中心的垂直线，即垂直方向的直径，所以定位基准与对称度的设计基准重合，0=∆JB ；又由于V 形块具有自动对中作用，外圆的中心仅在垂直方向上产生位置偏差，不会在水平方向上产生偏移，所以0=∆JW 。

） 所以能保证对称度的加工精度要求。

由此可见，第一种定位方案能同时保证上述两个加工精度要求。

2、采用第二种定位方案（见c 图）时，因定位销轴水平放置，属于单边固定接触。

（1）对于尺寸014.054-的定位误差： ）（047.0314.0085.0)202.003.0()21.0202.0(=≥=+++=∆+∆=∆JW JB DW （注：由于用销轴对工件内孔进行定位，定位基准是工件内孔的中心，而设计基准是工件外圆的下母线，所以基准不重合，另外要注意到根据题目的提示：内孔与外圆还存在着同轴度公差，同轴度公差是指任意直径方向上，所以基准不重合误差既要考虑到工件外圆半径公差，还要考虑到同轴度公差在半径方向上所产生的最大偏差）所以不能保证尺寸014.054-的加工精度要求。

（2）对于对称度的定位误差： ）（01.0303.002.0002.0=≥=+=∆+∆=∆JW JB DW （注：由于销轴对工件内孔定位时，其定位基准就是内孔中心，而对称度的设计基准是外圆的中心，即垂直方向的直径，当外圆的中心与内孔的中心在水平方向上产生最大的同轴度误差时，定位基准与对称度的设计基准不重合，02.0=∆JB ；又由于水平放置的销轴也具有自动对中作用，内孔的中心仅在垂直方向上产生位置偏差，不会在水平方向上产生偏移，所以0=∆JW 。