定位误差分析与计算.
- 格式:doc
- 大小:45.50 KB
- 文档页数:5


定位误差的分析与计算一、定位误差的概念和原因定位误差是指定位系统测量结果与真实位置之间的差异或偏差。
在现代生活中,定位系统广泛应用于导航系统、无人驾驶、无人飞行器等领域,而定位误差对于系统的准确性和可靠性至关重要。
1.信号传播误差:这是由于信号在传播过程中受到大气中的影响,如电离层、大气湿度等所产生的误差。
这种误差对于GPS系统尤为明显,导致多径效应、钟差误差等。
2.接收机误差:接收机的硬件和软件系统可能存在不同程度的误差。
硬件方面,接收机的时钟精度、天线阻抗匹配等问题都可能导致定位误差。
软件方面,接收机的算法、数据处理等也可能引入误差。
3.观测误差:观测误差是指由于测量设备的精度或不完善性所导致的误差。
例如,测量设备的精度限制了对信号强度、TOA(Time of Arrival)等参数的准确测量。
4.环境因素:环境因素也是定位误差产生的原因之一、比如,建筑物、树木、走廊等物体会对信号传播产生阻碍和衍射,从而影响接收机的测量结果。
5.多径效应:多径效应是指信号传播过程中,信号除了直射到达接收机外,还经历了反射,导致信号的多个传播路径同时到达接收机。
多径效应会产生明显的信号干扰和测量误差。
二、定位误差的计算方法1.位置误差计算:位置误差是指实际测量位置与真实位置之间的距离差异。
一种常见的计算方法是通过比较GPS测量点与参考点之间的差异来计算位置误差。
通过收集多个测量点的数据,可以使用最小二乘法进行曲线拟合,从而计算出测量点与真实位置之间的距离差异。
2.时间误差计算:时间误差是指实际测量时间与真实时间之间的差异。
在GPS系统中,时间误差主要由于卫星钟的钟差所引起。
通过GPS接收机接收到的卫星信号的时间戳和GPS接收机内部的时间戳之间的差异,可以计算出时间误差。
4.误差修正算法:为了减小定位误差,可以使用一些误差修正算法来对测量结果进行修正。
一种常见的方法是差分GPS技术,通过使用两个或多个接收机接收同一卫星信号,对测量结果进行差分处理,从而减小定位误差。
华北航天工业学院教案教研室:机制工艺授课教师:陈明第十章机床夹具的设计原理第三节定位误差的分析与计算一批工件逐个在夹具上定位时,各个工件在夹具上所占据的位置不可能完全一致,以致使加工后各工件的加工尺寸存在误差,这种因工件定位而产生的工序基准在工序尺寸上的最大变动量,称为定位误差,用∆D表示。
一、定位误差的组成1.基准不重合误差如前所述,当定位基准与设计基准不重合时便产生基准不重合误差。
因此选择定位基准时应尽量与设计基准相重合。
当被加工工件的工艺过程确定以后,各工序的工序尺寸也就随之而定,此时在工艺文件上,设计基准便转化为工序基准。
设计夹具时,应当使定位基准与工序基准重合。
当定位基准与工序基准不重合时,也将产生基准不重合误差,其大小对于定位基准与工序基准之间尺寸的公差,用∆B表示。
工序基准与定位基准之间的尺寸就称为定位尺寸。
2.基准位移误差工件在夹具中定位时,由于工件定位基面与夹具上定位元件限位基面的制造公差和最小配合间隙的影响,从而使各个工件的位置不一致,给加工尺寸造成误差,这个误差称为基准位移误差,用∆Y表示。
基准位移误差的大小对应于因工件内孔轴线与心轴轴线不重合所造成的工序尺寸最大变动量。
当定位基准的变动方向与工序尺寸的方向相同时,基准位移误差等于定位基准的变动范围,即∆Y = ∆i当定位基准的变动方向与工序尺寸的方向不同时,基准位移误差等于定位基准的变动范围在加工尺寸方向上的投影,即∆Y = ∆i cos a二、各种定位方式下定位误差的计算1.定位误差的计算方法如上所述,定位误差由基准不重合误差与基准位移误差两项组合而成。
计算时,先分别算出∆B和∆Y,然后将两者组合而成∆D。
组合方法为:如果工序基准不在定位基面上:∆D =∆Y + ∆B如果工序基准在定位基面上:∆D = ∆Y±∆B式中“+”、“-”号的确定方法如下:1)1)分析定位基面直径由小变大(或由大变小)时,定位基准的变动方向。




定位误差分析与计算一、基本概念定位误差分析是针对某一个工序的工序尺寸而言的,只要该工序尺寸不因定位而产生误差,那么就认为该工序尺寸的定位误差是零。
至于该工序尺寸在加工过程中产生的误差,则不属于定位误差的研究范畴。
所以,不应将定位误差与加工过程误差以及其它误差混为一谈。
1.定位误差△D(△dw):工件在夹具上(或机床上)定位不准确而引起的加工误差称之为定位误差。
其大小等于按调整法加工一批工件而定位时工序尺寸的最大变动量。
定位误差来源于两个方面:基准不重合误差和基准位移误差。
2.基准不重合误差△B(△jb):因工序基准与定位基准不重合(原因),用调整法加工一批工件时(条件),引起工序基准相对定位基准在工序尺寸方向上的最大变动量 (结果),称为基准不重合误差。
若把工序基准与定位基准之间的联系尺寸(基本尺寸)称之为“定位尺寸”,则△B就是定位尺寸的公差在工序尺寸方向上的投影(或者说定位尺寸的最大变动量在工序尺寸方向上的投影)。
注意:基准不重合误差中的工序基准和定位基准都是针对工件而言的,与定位元件无关;3.基准位移误差△Y(△db):因定位副制造不准确(原因),用调整法加工一批工件时(条件),引起工序基准在工序尺寸方向上的最大变动量(结果),称为基准位移误差。
(或者说工序基准位置的最大变动量在工序尺寸方向上的投影)。
基准位移误差可以划分为两类:工件定位表面制造不准确引起的基准位移误差和夹具定位元件表面制造不准确引起的基准位移误差。
注意:在基准位移误差计算中,工序基准的变动是因为定位基准的变动而引起的。
所以有学者认为:基准位移误差是指定位基准在工序尺寸方向上的最大变动量。
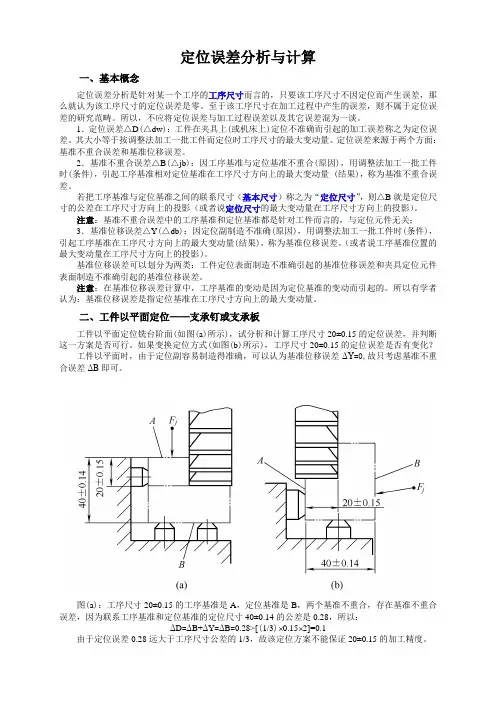
二、工件以平面定位——支承钉或支承板工件以平面定位铣台阶面(如图(a)所示),试分析和计算工序尺寸20±0.15的定位误差,并判断这一方案是否可行。
如果变换定位方式(如图(b)所示),工序尺寸20±0.15的定位误差是否有变化?工件以平面时,由于定位副容易制造得准确,可以认为基准位移误差ΔY=0,故只考虑基准不重合误差ΔB即可。



定位误差分析计算所谓定位误差,是指由于工件定位造成的加工面相对工序基准的位置误差。
因为对一批工件来说,刀具经调整后位置是不动的,即被加工表面的位置相对于定位基准是不变的,所以定位误差就是工序基准在加工尺寸方向上的最大变动量。
㈠引言①△总≤δ其中△总为多种原因产生的误差总和,δ是工件被加工尺寸的公差,△总包括夹具在机床上的装夹误差,工件在夹具中的定位误差和夹紧误差,机床调整误差,工艺系统的弹性变形和热变形误差,机床和刀具的制造误差及磨损误差等。
②△定+ω≤δ 其中,ω除定位误差外,其他因素引起的误差总和,可按加工经济精度查表确定。
所以由①和②知道:△定≤δ-ω(是验算加工工件合格与否的公式)或者:△定≤1/3δ(也是验算加工工件合格与否的公式)㈡定位误差的组成1、定义:定位误差是工件在夹具中定位,由于定位不准造成的加工面相对于工序基准沿加工要求方向上的最大位置变动量。
2、定位误差的组成:1) 定位基准与工序基准不一致所引起的定位误差,称基准不重合误差,即工序基准相对定位基准在加工尺寸方向上的最大变动量,以△不表示。
图示零件,设e面已加工好,今在铣床上用调整法加工f面和g面。
在加工f面时若选e面为定位基准,则f面的设计基准和定位基准都是e面,基准重合,没有基准不重合误差,尺寸A的制造公差为TA。
加工g 面时,定位基准有两种不同的选择方案,一种方案(方案Ⅰ)加工时选用f面作为定位基准,定位基准与设计基准重合,没有基准不重合误差,尺寸B的制造公差为TB;但这种定位方式的夹具结构复杂,夹紧力的作用方向与铣削力方向相反,不够合理,操作也不方便。
另一种方案(方案Ⅱ)是选用e面作为定位基准来加工g面,此时,工序尺寸C是直接得到的,尺寸B是间接得到的,由于定位基准e与设计基准f不重合而给g面加工带来的基准不重合误差等于设计基准f面相对于定位基准e面在尺寸B方向上的最大变动量TA。
定位基准与设计基准不重合时所产生的基准不重合误差,只有在采用调整法加工时才会产生,在试切法加工中不会产生。
4.4 定位误差分析与计算在机械加工过程中,使用夹具的目的是为保证工件的加工精度。
那么,在设计定位方案时,工件除了正确地选择定位基准和定位元件之外,还应使选择的定位方式必须能满足工件加工精度要求。
因此,需要对定位方式所产生的定位误差进行定量地分析与计算,以确定所选择的定位方式是否合理。
4.4.1 定位误差产生的原因和计算造成定位误差ΔD的原因可分为性质不同的两个部分:一是由于基准不重合而产生的误差,称为基准不重合误差ΔB;二是由于定位副制造误差,而引起定位基准的位移,称为基准位移误差ΔY。
当定位误差ΔD≤1/3δK(δK为本工序要求保证的工序尺寸的公差)时,一般认为选定的定位方式可行。
(1) 基准不重合误差的计算由于定位基准与工序基准不重合而造成的工序基准对于定位基准在工序尺寸方向上的最大可能变化量,称为基准不重合误差,以ΔB表示。
如图4.36所示的零件简图,在工件上铣一通槽,要求保证的工序尺寸为A、B、C,为保证B尺寸,工件用以K1面或以K2面来定位,都可以限制工件在B尺寸方向上的移动自由度。
但两种定位方式的定位精度是不一样的。
由于加工过程中,是采用夹具上定位件的定位表面为基准来对刀的。
当以K1面为定位基准时,如图 4.37(a)所示B就为确定刀具与夹具相互位置的对刀尺寸,在一批工件的加工过程中B的位置是不变的。
当以K2面为定位基准时,如图4.37(b)所示B′为确定刀具与夹具相互位置的对刀尺寸,由于工序基准是K1面,与K2面不重合。
当一批工件逐个在夹具上定位时,受尺寸L±Δl的影响,工序基准K1面的位置是变动的,K1的变动影响工序尺寸B的大小,给B造成误差。
由图 4.37(a)可知ΔB=0由图 4.37(b)可知ΔB=Lmax-Lmin=2Δl(4.1)当工序基准的变动方向与工序尺寸方向有一夹角时,基准不重合误差等于定位基准与工序基准间距离尺寸公差在工序尺寸方向上的投影,即Δ B= (Smax-Smin)cos ββ是基准不重合误差变化方向与工序尺寸方向上夹角( 2)基准位移误差和计算由于定位副的制造误差而造成定位基准对其规定位置的最大可能变动位移,称为基准位移误差,用ΔY来表示。
4.4 定位误差分析与计算
在机械加工过程中,使用夹具的目的是为保证工件的加工精度。
那么,在设计定位方案时,工件除了正确地选择定位基准和定位元件之外,还应使选择的定位方式必须能满足工件加工精度要求。
因此,需要对定位方式所产生的定位误差进行定量地分析与计算,以确定所选择的定位方式是否合理。
4.4.1 定位误差产生的原因和计算
造成定位误差Δ D的原因可分为性质不同的两个部分:一是由于基准不重合而产生的误差,称为基准不重合误差Δ B;二是由于定位副制造误差,而引起定位基准的位移,称为基准位移误差Δ Y。
当定位误差Δ D≤1/3δK(δK为本工序要求保证的工序尺寸的公差)时,一般认为选定的定位方式可行。
(1 基准不重合误差的计算
由于定位基准与工序基准不重合而造成的工序基准对于定位基准在工序尺寸方向上的最大可能变化量,称为基准不重合误差,以ΔB表示。
如图4.36所示的零件简图,在工件上铣一通槽,要求保证的工序尺寸为A、B、C,为保证B尺寸,工件用以K1面或以K2面来定位,都可以限制工件在B尺寸方向上的移动自由度。
但两种定位方式的定位精度是不一样的。
由于加工过程中,是采用夹具上定位件的定位表面为基准来对刀的。
当以K1面为定位基准时,
如图 4.37(a)所示B就为确定刀具与夹具相互位置的对刀尺寸,在一批工件的加工过程中 B的位置是不变的。
当以K2面为定位基准时,如图4.37(b)所示B′为确定刀具与夹具相互位置的对刀尺寸,由于工序基准是K1面,与K2面不重合。
当一批工件逐个在夹具上定位时,受尺寸L±Δl的影响,工序基准K1面的位置是变动的,K1的变动影响工序尺寸B 的大小,给B造成误差。
由图 4.37(a可知ΔB=0
由图 4.37(b可知ΔB=Lmax-Lmin=2Δl (4.1)
当工序基准的变动方向与工序尺寸方向有一夹角时,基准不重合误差等于定位基准与工序基准间距离尺寸公差在工序尺寸方向上的投影,即
Δ B= (Smax-Smincos β β是基准不重合误差变化方向与工序尺寸方向上夹角
( 2)基准位移误差和计算
由于定位副的制造误差而造成定位基准对其规定位置的最大可能变动位移,称为基准位移误差,用ΔY 来表示。
显然不同的定位方式和不同的定位副结构,其定位基准的移动量的计算方法是不同的。
下面分析几种常见的定位方式产生的基准位移误差的计算方法。
1)工件以平面定位工件以平面为定位基准时,若平面为粗糙表面则计算其定位误差没有意义;若平面为已加工表面则其与定位基准面的配合较好,误差很小,可以忽略不计。
即工件以平面定位时,
ΔY=0 (4.2
2)工件以圆孔在圆柱销、圆柱心轴上定位或工件以外圆柱面在圆孔上定位
工件以圆孔在圆柱销、圆柱心轴上定位,其定位基准为孔的中心线,定位基面为内孔表面。
如图 4.38所示,设工件的圆孔为ФD +δ D ,定位件的轴径尺寸为Фd -δ d 。
由于定位副配合间隙的影响,会使工件上圆孔中心线(定位基准的位置发生偏移,当孔的尺寸为最大值,轴径尺寸为最小值时,其中心的可能偏移量即基准位移误差Δ y最大。
Δ Y =ФDmax一Фdmin= δ D + δ d十Xmin…………………………(4.3
Xmin--定位所需最小间隙(设计时确定),mm。
Xmin=ФDmin-Фdmax
其定位基准可以在任意方向上偏移,即Δ Y误差的对任意方向的工序尺寸都有影响
当工件用水平圆柱心轴定位时,相反,工件以外圆柱面在圆孔上定位,其Δ Y的计算为
Δ Y= ( δ D + δ d+Xmin/2 (4.4
相反,工件以外圆柱面在圆孔上定位,其Δ Y的计算为
Δ Y =ФDmax一Фdmin= δ D + δ d十Xmin (4.5
不过δ D 是定位件圆孔的极限尺寸,δ d 是工件外圆柱面的极限尺寸.而其Δ Y 误差同样对任意方向的工序尺寸都有影响
3)工件以外圆柱面在v形块上定位
工件以外圆柱面在 v形块上定位时,其定位基准为工件外圆柱面的轴心线,定位基面为外圆柱面。
若不计 V形块的制造误差,由于V形块的对中性则
Δ Y(对称面水平方向上=0 (4.6
而由于工件基准面的形状和尺寸误差时,工件的定位基准会在对称面上产生偏移,如图4.39所示,即在Z向的基准位移量可由下式计算
Δ Y = OOˊ=δ d/2sin(α/2) (4.7
其中δ d——工件定位基面的直径公差,mm;
α——V形块的夹角,( ° 。
ΔY的误差变化方向在V形块的对称面上
(3)定位误差的计算
由于定位误差ΔD是由基准不重合误差和基准位移误差组合而成的,因此在计算定位误差时,先分别算出Δ B和ΔY ,然后将两者组合而得ΔD。
组合时可有如下情况。
1Δ Y ≠ 0,Δ B=O时Δ D= Δ B (4.8
2ΔY =O,Δ B ≠ O时Δ D= Δ Y (4.9
3Δ Y ≠ 0, Δ B ≠ O时
如果工序基准不在定位基面上Δ D=Δ y + Δ B (4.10
如果工序基准在定位基面上Δ D=Δ y ±Δ B (4.11
“ + ” ,“—” 的判别方法为:
① 设定位基准是理想状态,当定位基面上尺寸由最大实体尺寸变为最小实体尺寸(或由小变大时,判断工序基准相对于定位基准的变动方向。
② 设工序基准是理想状态,当定位基面上尺寸由最大实体尺寸变为最小实体尺寸(或由小变大时,判断定位基准相对其规定位置的变动方向。
③ 若两者变动方向相同即取“ + ” ,两者变动方向相反即取“—”。