当前位置：文档之家 › 固体物理学：自由电子费米气体

固体物理学：自由电子费米气体

  • 格式：ppt
  • 大小：2.97 MB
  • 文档页数：116

下载文档原格式

  / 116

合集下载

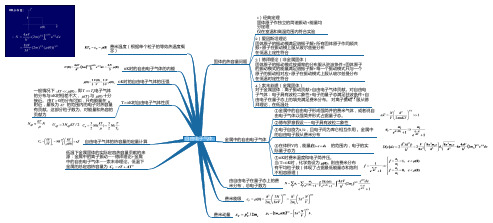
金属中自由电子气体

金属中自由电子气体

1）经典定理固体原子作独立的简谐振动+能量均分定理仅在室温和高温范围内符合实验2）爱因斯坦理论固体原子的振动模满足谐振子解+所有固体原子作同频共振+原子在振动模上服从玻尔兹曼分布在低温上定性符合3）德拜理论（非金属固体）固体原子的振动模式按频率的分布服从驻波条件+固体原子的振动模式的能量满足谐振子解+每一个振动模式只与一个原子的振动相对应+原子在振动模式上服从玻尔兹曼分布在低温时定性符合4）索末菲理（金属固体）对于金属固体：离子振动贡献+自由电子气体贡献。

对自由电子气体：电子具有波粒二象性+电子的量子态满足驻波条件+自由电子在量子态上的填充满足费米分布。

对离子振动：服从德拜理论，在低温处①金属中的自由电子形成强简并的费米气体，或者说自由电子气体以强简并形式占据量子态。

②德布罗意假设——电子具有波粒二象性③电子自旋为1/2，且电子间为库仑相互作用。

金属中的自由电子服从费米分布④在体积V 内，能量在的范围内，电子的实际量子态为⑤0K 时费米温度和电子简并压。

当T=0K 时，化学势设为，则由费米分布有平均粒子数（体现了占据最低能量态和泡利不相容原理）一般情况下，，即电子气体的分布与0K 时相差不大，与十分接近。

由的分布可知，只有能量在附近，量级为的范围内的电子对热容量有贡献。

这部分粒子数为、对能量和热容的贡献为固体的热容量问题金属中的自由电子气体由自由电子在量子态上的费米分布，总电子数为费米能级费米动量费米温度（根据单个粒子的等效热温度概念）0K 时的自由电子气体的内能0K 时的自由电子气体的压强T>0K 时自由电子气体性质自由电子气体的热容量的定量计算低温下金属固体的实际定容热容量贡献的来源：金属中的离子振动——德拜理论+金属中的自由电子气体——索末菲理论。

低温下金属的总定容热容量为自由电子气体。

固体物理学课件：第五章 金属自由电子论

固体物理学课件：第五章 金属自由电子论

所以
0
M H
N
EF0
0
2 B
0
3N 0B2
2EF0
N
EF0
3N 2EF0
由于BB << EF0，所以，我们再次看到对电子Pauli 顺磁有贡献的并不是金属所有的自由电子，而只是在费 米面附近的一小部分电子。
3. 导电率
当＝0时，费米球的球心在原点，这时，任何一 个量子态k，都有一个反方向的－k态与之对应，处在 这两种量子态的电子具有大小相等、方向相反的速度， 所以，系统的总电流为0。
3. 能态密度
E k
2k 2
2
2m 2m
kx2
k
2 y
kz2
这表明，在k空间中，自由电子的等能面为球面，在能 量为E的球体中，波矢k的取值总数为
k 4k3
3
每一个k的取值确定一个电子能级，若考虑电子自旋， 根据Pauli原理每一个能级可以填充自旋方向相反的两 个电子。如将每一个自旋态看作一个能态，那么，能 量为E的球体中，电子能态总数为
2. Pauli顺磁 这里只考虑T 0的极端情况。
当B=0时，由于电子 自旋方向相反的两种 取向的几率相等，所 以，整个系统不显示 磁性，即M=0。
E
- B
E0
F
当B 0时，自旋磁矩 在磁场中的取向能：
N(E)/2
0
B=0
B
N(E)/2
B平行于B： －BB； B反平行于B： ＋ BB
导致两种自旋电子的能级图发生移动，相应的费米 能相差2 BB。因此，电子的填充情况要重新调整， 即有一部分电子从自旋磁矩反平行于B转到平行于B 的方向，最后使两边的费米能相等。
f E
E

第五章：金属的电子理论

第五章：金属的电子理论

dN ( E ) 3 2me 2 dE 2
3/ 2
3/ 2
E1/ 2
V 3 2
V 2me 2 2 2 3N ( E ) 2E
E1/ 2
DOS: number of electrons/unit energy in a range E ~ E + dE
自由电子模型总结
• 即使在金属中，传导电子的电荷分布（ charge distribution）收到 离子芯强烈静电势的影响。因此，自由电子模型描述传导电子的运 动特性（kinetic properties）最为合适。传导电子与离子之间的相 互作用将在能带理论中讨论。 • 最简单的金属是碱金属：Li, Na, K, Rb, Cs。在这些单价金属中，N 原子构成的晶体有N 个电子和N 个正离子。 • 自由电子模型产生于在量子理论建立之前。经典Drude模型成功导 出欧姆定律（Ohm’s law），以及电导和热导的关系。但是，由于 使用了Maxwell经典统计分布，它不能解释比热容（heat capacity） 和磁化率（magnetic susceptibility ）。后来Sommerfeld在量子理 论基础上重建了该模型。
~ 10eV
1/ 3 2 pF kF 3 N ~ 108 cm / sec vF V me me me
2/3 2 2 2 EF 2 3 N ~ 105 K TF kF kB 2me kB 2me kB V
态密度（Density of states, DOS）
L N (E) 2 2
dN ( E ) L 2me 1 N ( E ) 2me E , D( E ) dE E 2

费米气体

费米气体

统计规律
费米气体的统计规律有：费米-狄拉克统计，非广延统计。
费米气体是理想气体的量子力学版。在金属内的电子、在半导体内的电子、或在中子星里的中子，都可以被 视为近似于费米气体。在一个处于热力平衡的费米气体里，费米子的能量分布，是由它们的密度，温度，与容许 能量量子态集合，依照费米-狄拉克分布方程而决定的。泡利不相容原理阐明，不容许被两个或以上的费米子占用 同一个量子态。因此，在绝对零度，费米气体的总能量，大于费米子数量与单独粒子基态能量的乘积。并且，在 绝对零度，费米气体的压力，称为“简并压力”，不等于零。这与经典理想气体的现象有很明显的不同。简并压 力使得中子星或白矮星能够抵抗万有引力的压缩，因而得到稳定平衡，不致向内爆塌。
感谢观看
简介
费米气体是借用理想气体模型描述费米子系统性质的量子力学模型。该模型中，粒子所处的量子态可用它们 具有的动量来表征。对于周期性系统，譬如在金属原子点阵中运动的电子，亦可类似地引入“准动量”的概念以 表征量子态（参见条目布洛赫波）。无论上述哪种模型，其具有费米能的量子态都处于动量空间中的一个确定的 曲面上，这个曲面称为费米面。费米气体的费米面是一个球面；周期体系中的费米面则通常是扭曲面。费米面包 围的体积决定了系统中的电子数，而费米面的拓扑结构则与金属的各种传导性质（如电导率）直接相关。对费米 面的研究有时被称为“费米学”（Fermiology）。如今，绝大多数金属的费米面均已经有较透彻的理论与实验研 究。
由于前述定义忽略了粒子与粒子之间的相互作用，费米气体问题约化为研究一群独立的费米子的物理行为的 问题。这问题本身相当容易解析。一些更深奥，更进阶，更精密的理论，牵涉到粒子与粒子之间的互相作用的理 论（像费米液体理论或相互作用的微扰理论），时常会以费米气体问题为研究的开端。

固体物理(第11课)索末菲模型

固体物理(第11课)索末菲模型

5.2.2 单电子的本征态和本征能量
1.电子气的本征态 ˆ 设F为算符，U为一个函数， 为常数。 设一金属为立方体，其 边长为L。且有： ˆ U U，则称为算符F的本征 ˆ 2 若有F
表示空间某点处单位体 积元中粒子出现的
0 x,y,z L 0 值，U为算符F的本征函数，而此时 ˆ U 2 V ( x, y, z ) 几率，波函数归一化条 件： dr 1 x,y,z 0或x,y,z 态称为本征态。 函数对应的粒子运动状 L ˆ H E 在金属内部有：
ik r
N
2 nx 2 n y 2 nz k I J K L L L
k空间 波矢空间 状态空间
nx Kx L1 ny Ky L2 nz Kz L3
其中
nx n y 0,1,2 nz
在恒定势场条件下，即V x, y , z, t V x, y , z 波函数应有以下形式： ( x, y , z, t ) e
E i t
2. 定态薛定谔方程：
其空间部分ψ ψ(x , y , z)应满足如下方程： 2 2 V x, y , z E , 定态薛定谔方程 2 2m x ( x, y , z ) 粒子的定态波函数
2 i ( pr Et ) Ae 进行二次偏微商 ,得到 2 Ap x 2 i ( p x x p y y p z z Et ) e
2 t
同理有
2 px 2 ( r, t ) 2 p2 y 2 ( r, t ) t 2
L 3. 单位体积对应的量子态数目： 2 2

固体物理

固体物理

第一章晶体结构⏹布拉菲点阵概念⏹惯用晶胞（单胞）概念⏹初基晶胞（原胞）概念⏹Wigner-Seize晶胞⏹晶体结构基元+点阵=晶体结构⏹简单的晶体结构（1）sc，bcc，fcc结构的特征（2）金刚石结构（3）六角密堆积结构（4）NaCl结构（5）CsCl结构⏹晶列, 晶向, 晶面, 晶面族, 晶面指数, 密勒指数, 晶面间距晶面指数（hkl)的定义和求法方向指数[abc]的定义和求法⏹对称操作⏹7种晶系和14种布拉菲点阵1以堆积模型计算由同种原子构成的同体积的简立方和面心立方晶体中的原子数之比。

2证明立方晶系的晶列[hkl]与晶面族(hkl)正交3某元素晶体的结构为体心立方布拉菲格子，试指出其格点面密度最大的晶面系的密勒指数，并求出该晶面系相邻晶面的面间距4在立方晶胞中画出（122），（001），（10），（210）晶面和[122]5晶体中可以独立存在的8种对称元素是：、、、、、、、。

⏹布拉格定理⏹倒易点阵初基矢量公式⏹布里渊区的求法（二维正方格子和长方格子）⏹实验衍射方法（劳厄法、转动晶体法和粉末法）⏹倒易点阵矢量和晶面指数间的关系1考虑晶体中一组互相平行的点阵平面（hkl），（a）证明倒易点阵矢量G（hkl）=hb1+kb2+lb3垂直于这组平面（hkl）；（b）证明两个相邻的点阵平面间的距离d（hkl）为2从体心立方铁的（110）平面来的X-射线反射的布喇格角为22º，X-射线波长λ=1.54Å。

试计算铁的立方晶胞边长；(b）从体心立方结构铁的(111)平面来的反射的布喇格角是多少？答案：a）a=2.91Å；b）θ=27.28º3对于点阵常数为a的二维六角点阵，（a）写出正点阵的初基矢量；（b ）计算倒易点阵的初基矢量；（c ）画出第一、第二、第三布里渊区；（d ）计算第一布里渊区的体积。

4半导体材料Si 和Ge 单晶的晶体点阵类型为 ，倒易点阵类型为 ，第一布里渊区的形状为 ，每个 原子的最近邻原子数为 。

固体物理第二章金属自由电子论


u为平均附加速度: v
v :电场附加给电子的平均速度(平均附加速度)。?? 10
考虑某一个电子，从上次碰撞发生起，有t时间的行 程。如果无外电场，其速度为v0。根据特鲁德模型德假 设，碰撞后电子出现的方向是随机的，因此v0将对总体 的电子平均速度毫无影响，即：
v0 0
但在外电场存在条件下，在上一次碰撞后立即附加
上一个速度：
eEt vt m
(E为外加电场，m为电子质量)。因此电子平均速度 只是由各电子的附加速度取平均获得。
vv0vt
eE
m
t2 t1
11
欧姆定律E=j ，其中E为外加电场强度、为电阻率、j 为电流密度。
成功用微观量解释了宏观量！
12
特鲁德模型的其他成功之处
Nat. Photon. 1, 641, 2007
EF0 ~ 几个eV
定义 Fermi 温度：
TF
E
0 F
kB
物理意义：设想将EF0转换成热振动能，相当于多高温度 下的振动能。
金属：TF： 104 ~ 105 K 36
一些金属元素费米能与费米温度的计算值
元素
Li Na K Rb Cs Cu Ag Au Be
EF0 (eV) 4.72 3.23 2.12 1.85 1.58 7.00 5.48 5.51 14.14
怎么求dN！ 接下来问题就来了！ dU EdN
Here comes the problem U EdN
16
§2.2 Sommerfeld的自由电子论
核心问题
怎么求dN！
对于理想气体貌似有某个方法 对于dV范围内的分子数为： dN=dV内分子密度×dV
对于dE范围内的：

17.1 自由电子气体模型


dN
N

F
0
3
F3

3d

3 4
F
单位体积内, 能量区间 E~E+dE 内的状态数
dNE g(E)dE V
g(E)
dNE VdE

(2me )3/2
2 2 3
E1/2
-- 态密度
电子是按能量规则地从低向高排布， 一个态一个电子（泡利不相容原理）
能量区间 E~E+dE 电子数密度
金属自由电子气体模型
平均场近似下，金属原子的价电子是在均
匀的势场中运动，金属表面对电子可近似看作 无限高势垒。(功函数远大于电子动能)
这些价电子称为自由电子。
U

0
内部 外部
如果考虑立方体形状，N个自由电子好象 是装在三维盒子里的气体。
L L
每个电子都要满足驻波条件
L

nx 2
x
kxL nx
dN E V

g(E)dE 0
E EF E EF
小于费米能量，电子数 = 状态数 小于费米能量态，电子占据几率 1
大于费米能量态，电子占据几率 0
f(E) 1
T=0
0 系统 T = 0
EF E
编者： 安宇
§1 自由电子气体按能量的分布
金属中的电子受到周期排布的晶格上离子 库仑力的作用。
一晶 维格 晶、 体点
阵
U(x)
21
21
考虑电子受离子与其它电子的(2) 电子的运动有隧道效应
(1) 蕊电子 (2) 价电子
价电子的势垒穿透概率较大 在整个固体中运动, 称为共有化电子
(2,1,1) (1,2,1) (1,1,2)

自由电子模型在固体物理学中的应用

自由电子模型在固体物理学中的应用自由电子模型是固体物理学中的重要理论之一，它可以帮助我们理解固体的电子结构和导电性质。

在这篇文章中，我们将探讨自由电子模型的基本原理以及其在固体物理学中的应用。

首先，让我们来了解一下自由电子模型的基本原理。

根据这个模型，固体中的原子贡献到电子结构的唯一方式是通过它们最外层的价电子。

在自由电子模型中，我们假设固体中的电子几乎完全自由地运动，就像在真空中一样。

这意味着电子之间没有相互作用，也没有受到晶格的束缚。

通过这个简化的模型，我们可以解释许多固体的重要性质。

首先是电子的能带结构。

当我们考虑到每个原子贡献的电子数时，我们可以得到能量与动量的关系。

这个关系被描述为能带结构，指的是一段能量范围内允许存在电子的能量带。

在能带结构中，我们可以看到费米能级的存在。

费米能级是指在绝对零度时，处于占据态和空位态之间的能级。

它决定了固体的导电性质。

当我们加入能量到系统中，例如通过温度，电子将从占据态变为空位态。

费米能级以上的电子可以参与传导，而以下的不能。

这解释了为什么某些固体是良好的导体，而其他的是绝缘体或半导体。

与能带结构相关的一个重要现象是禁带。

禁带是指能带之间的能量范围，其中不存在电子能级。

这解释了为什么某些固体无法导电，因为它们的能带结构中没有可用的电子态。

此外，自由电子模型还可以解释电子在固体中的运动性质，如电子的有效质量和迁移率。

有效质量指的是在固体中运动的电子与在真空中自由运动的电子之间的等效质量。

迁移率是描述电子运动难易程度的物理量。

虽然自由电子模型是一个简化的模型，但它为我们提供了理解固体物理学中的许多现象的基本框架。

它为我们提供了解释导电性、光学性质、热导率和磁性等多种性质的途径。

然而，我们也必须意识到自由电子模型的局限性。

它忽略了电子之间的相互作用和晶格的影响，这在某些情况下可能是不合适的。

因此，在更加复杂的系统中，我们需要借助其他更精确的理论和模型来深入研究固体物理学的问题。

固体物理第一章课件


1
3
E = V ∫0 g ( E ) EdE = V ∫0
F
E
E
F
E 2m3 2m3 E 2m 3 2 2 F 2 EdE = V E dE = V E ∫ 0 π2ℏ 3 π2 ℏ 3 π2 ℏ 3 5 F
3
5
E=3E N 5 F
能态密度的更一般形式
g ( E )= dN dE
E k =const.
NZ NZ NZ
自由电子模型的物理思想
◆ 自由电子近似 离子静止，忽略电子和离子实之间的相互作用，电子运动范围 仅受限于晶体表面势垒，被限制在晶体内部 ◆ 独立电子近似 忽略电子和电子之间的相互作用 ◆ 驰豫时间近似
Zn Zm ℏ2 e2 H= −∑ ∇n 2 + ∑′ 1 2 n, m 4πε0 R − R n =1 2M n n m Zn e2 ℏ 2 2 e2 1 1 1 −∑ ∇i + ∑′ −∑∑ 2 i =1 2m i , j 4πε r − r i =1 n=1 4πε r − R i 0 i 0 i j n
kF = 3π2 ne
ℏ 2 kF 2 2m
1/3
108cm -1 2~10eV
费米能量：
EF=
费米动量： 费米速度： 费米温度：
pF = ℏk F
υF = ℏkF /m T F = EF / k B
108cm/s 104 ~105 K 参见表 1.1
单位体积内的平均能量
T=0时，单位体积内的平均能量为：
Drude 模型：应用经典力学，服从经典统计，麦克斯韦- 玻耳兹曼分布 Sommerfeld 模型：应用量子理论，服从量子统计，费米-狄拉克分布
f ( E )= e
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
释了金属的高电导率、高热导率、霍尔效应以及某些光学性 质。
14
不足之处： 获得的平均自由程和热容与实验结果严重不符，实验 上热容仅是理论值的1%(电子参与导电过程，但对热 导好像没有参与，为什么？）；在处理磁化率等问题 上也遇到根本性的困难。
不足之处产生的原因分析
经典理论在微观世界的不适用
15
量子力学对金属中电子的处理
2）忽略了电子与电子之间的库仑排斥相互作用， 成为独立电子近似（independent electron approximation）。
7
3） 传导电子简单地随机的和正离子实相碰撞(受正 离子实的散射)且碰撞是瞬时的，每次碰撞都急剧地 改变传导电子的速度，但碰后电子的速度只与碰撞 地点的温度有关，而与碰前速度无关。电子只是通 过碰撞与周围环境达到热平衡。在相继的两次碰撞 之间，电子做直线运动，遵循牛顿第二定律，称为 碰撞近似（collision approximation）。
12
3）金属的比热
特鲁德模型将金属中的电子视作经典粒子。根据经典的能 量均分定律：
—— 每个电子具有3个自由度，每个自由度具有kBT/2的 平均能量
—— 设单位体积内的电子数为n，则电子气系统的内能密
度为
U
3 2
nkBT
电子气的热容：
C Classical v
3 2
nkB
高温下与晶格振动的贡献相当， 这与实验结果不符。
4）一个电子与离子实两次碰撞之间的平均时间间隔 称为弛豫时间，它与电子的速度和位置无关，称为 弛豫时间近似（relaxation approximation）。
8
特鲁德模型的应用
1）金属的直流电导金属晶体内的电子运动类 似理想气体分子的运动，因此电流密度为
j = -nev平
n —— 金属导体内的电子数密度 v平—— 电子运动的平均定向速度
大多数金属
C Experimental V
/ CClassical V
0.01
13
4）特鲁德模型的发展：
1904年，洛伦兹发展了该模型，将麦克斯韦—玻尔 兹曼统计规律引人，认为电子速度服从麦克斯韦—玻尔兹
曼统计分布律。
5）特鲁德模型的成功与失败
成功之处：
经典的特鲁德—洛伦兹自由电子模型从微观上定性的解
16
2．Sommerfeld的自由电子论
索末菲模型的基本假设： 1）free electron approximation 2）independent approximation 3）价电子的能量分布服从费米—狄拉克统计，称为 自由电子费米气体（free electron Fermi gas） 4）不考虑电子和离子实的碰撞（no collision）
1926 年 费 米 — 狄 拉 克 统 计 理 论 和 量 子 力 学 建 立 ， 1928年，索末菲在自由电子模型基础上，提出应该 利用量子力学原理去计算电子气体的能量和动量， 并由此考察金属的一些特性。
索末菲提出：电子在离子产生的平均势场中运动， 电子气体服从费米 — 狄拉克分布和泡利不相容原理。 并成功地计算了电子的热容，解决了经典理论的困 难。
将金属中高浓度（1022-1023/cm3)的价电子看作理 想气体，其基本假设为：
1）金属晶体中的传导电子只与离子实发生碰撞 （后面可以看到，电子与电子之间的碰撞几率基本 可以忽略），忽略了离子实与传导电子之间的库仑 相互作用，称为自由电子近似（free electron approximation）。
2
许多固体具有导电性，这意味着在这固体内 有许多电子并没有真正被原子所束缚住，相反的 这些电子可以在固体内遨游。
具有导电性的固体可被区分成两类，那便是 金属与半导体。
在这章节内我们将只针对金属进行讨论。
3
§6.1 金属自由电子论
的物理模型
4
1. Drude的金属自由电子论
Drude的经典理论建立的历史背景: 1870年前后，玻尔兹曼、麦克斯韦等
Drude的经典理论: 自由电子是经典离子气体，服从玻尔
兹曼分布(速度分布)，与中性稀薄气体一 样去处理，完全套用经典气体模型，认为 电子之间无相互作用，同时也不考虑离子 实势场的作用。
这样一个简单的物理模型处理金属的 许多动力学问题是成功的，特别是对我们 理解简单金属的许多性质是有帮助的。
6
Drude经典理论的基本假设:Biblioteka v平eEtme
me——电子的质量
t ——传导电子与离子实发生碰撞的平均自由时间
ne2t
j nev平 me E
ne2t 1 me
j E E j 欧姆定律
10
2）金属的平均自由时间和平均自由程 ——实验测定金属的电阻率，来估计平均自由时间t
t
me
ne2
1015
1014 s
——平均自由程l (电子在连续两次碰撞之间的平均运动距离)
l v平t
——根据经典的能量均分定律，有
1 2
mev平2
3 2
kBT
l v平t 110 A
11
l v平t 110 A
free electron approximation
离子实（金属原子间距）大约也就是这个量级，可 以看出，与Drude模型的假设比较吻合。
——但实验中发现金属中电子的平均自由程要比以上特 鲁德模型的估算值大得多。Cu： T=4K， l 103 A 也就是Drude模型当中的假设并不是适用于一切情况。
建立了气体分子运动论和统计理论；1897 年，T.T.Thomson发现电子，使得人们轻 易就可以猜测出金属导电的机制。
在总结 金属本身总是具有高电导率、 高热导率和高的反射率的实验事实的基础 上，Drude于1900年建立了Drude模型，主 要研究金属的电导和热导问题。
5
1. Drude的金属自由电子论
讨论：
外电场E=0时， v平=0
电子运动是随机的
净定向电流为零，对电流密度没有贡献
9
外电场E≠ 0时， v平≠ 0 —— 产生净定向电流 在外场E作用下，考虑电子每一次碰撞后其运动方向是随机 的，所以电子的初速度对平均速度是没有贡献的。
因此，电子平均速度v平起源于在外场E作用下，电子在连续 两次碰撞的平均时间间隔内，电子附加上的一个速度：
第六章
自由电子费米气体 (金属自由电子论)
Free Electron Fermi Gas
金属元素有大约75种之多，在自然 界大约有2/3以上的固态纯元素属于
金属。
人类社会很早就学会了使用金属并 以其作为人类进步的标志，如过去的铜 器时代、铁器时代等。
金属具有良好的导电、导热、易加 工及特殊的金属光泽等特点，但为什么 这些元素具有如此的特点？其深层次的 原因是什么？