(36)光程 薄膜干涉

薄膜可以是固体的、液体的或气体的 ，只要其上下表面反射的光波能够发 生干涉即可。
等倾干涉的条件
1
入射光波必须是平行光束，即光束的入射角必须 相等。
2
薄膜的上下表面必须平行，即薄膜的倾角必须为 零。
3
入射光波在薄膜上下表面的反射必须满足干涉条 件，即光波的波长、入射角和薄膜的折射率必须 满足干涉相长的条件。
薄膜厚度的测量
薄膜厚度的精确测量
等倾干涉条纹的形状和间距与薄膜的厚度有关，通过测量干涉条纹的形状和间 距，可以精确测量薄膜的厚度。
薄膜生长过程的实时监测
在薄膜生长过程中，等倾干涉条纹可以实时监测薄膜的生长情况，为薄膜生长 工艺的控制提供依据。
其他应用领域
光学传感
等倾干涉条纹的形状和变化可以用于检测物理量如温度、压力、折射率等的变化 ，在光学传感领域有广泛的应用。
等倾干涉的原理
当一束光波入射到薄膜上 时，光波在薄膜上下表面 反射，形成两列相干光波。
当两列光波的相位差等于 2nπ（n为整数）时，它 们发生干涉相长，形成明 亮的干涉条纹。
ABCD
由于光波在薄膜上下表面 的反射路径不同，导致两 列光波的相位发生变化。
当两列光波的相位差不等 于2nπ时，它们发生干涉 相消，形成暗的干涉条纹。
薄膜干涉的形成
当光波入射到薄膜表面时，一部分光被反射，一 部分光透射进入薄膜内部。
反射光和透射光在薄膜表面再次相遇，由于光程 差的存在，它们会发生干涉。
当薄膜的厚度满足一定条件时，反射光和透射光 的光程差相等，形成等倾干涉现象。
03
等倾干涉现象
等倾干涉的定义
等倾干涉是指当一束光波入射到薄膜 上，在薄膜上下表面反射的光波发生 干涉的现象。

1.95 k 3.26
紫 红 色
k 2,
k 3,
2n1d 736 nm 2 1/ 2 2n1d 441 .6nm 3 1/ 2
红光 紫光

d
§11-3 光程 薄膜干涉
结论 （1）反射光的光程差 （2）透射光的光程差为
Δr 2n2 d cos r 2
1 2 3
Δt 2n2d cosr
说明当反射光干涉相互加强时， 透射光干涉相互减弱. 能量守恒!
4
5
注意：两束反射光只有一束有相位突变，则反射光之间 有附加的光程差/2，否则没有。 （3）光学元件的表面镀一层薄膜，制成增透膜或增反膜
相位跃变影响
k 相长( 最亮处) 2kπ 1 2 Δ (2k 1) (2k 1) π 2 相消( 最暗处)
k 0,1,2,
§11-3 光程 薄膜干涉
讨论: 杨氏双缝中，若有下列变动，干涉条纹将如何变化? （1） 把整个装置浸入水中 （2）光源S略微下移至S'，讨 S1 论条纹移动情况 ，若 S1S 'S d o' S2S'= ，求解明纹位置 x 表 S' S 2 达式以及SS' =? ；若S' 下移b， b' 则屏上中央明纹移动多少距 离？ （3） S1处加一透明介质片( n , t ) （4）两缝宽度稍有不等；
F
B
§11-3 光程 薄膜干涉
三 薄膜干涉
1 2 L 3 C E P
32 n2 ( AB BC) n1 AD
2
只有i=0或i=900
M1 M2
n1
n2
i
A

02
在等倾干涉中，光线在薄膜的上、下表面反射后发 生相干，形成干涉条纹。
03
等倾干涉广泛应用于光学仪器、光通信等领域，是 光学干涉技术中的重要组成部分。
等倾干涉的条件
1
入射光束必须为平行光束，且入射角相等。
2
薄膜必须具有一定的厚度，且上下表面反射率相 近。
3
入射光波长需满足一定条件，使得光在薄膜中发 生相干。
发展等倾干涉的数值模拟方法
利用计算机模拟等倾干涉现象，预测不同条件下的干涉结果，为实验设计和优化提供指 导。
等倾干涉的实验研究
探索新型的干涉实验技术和装置
开发更先进、更高效的实验装置和方法，提高干涉实验的精度和可靠性。
拓展等倾干涉的应用范围
将等倾干涉技术应用于更多领域，如光学传感、表面检测、生物医学等，发掘其潜在的应用价值。
感谢您的观看
THANKS
薄膜干涉的应用
01
02
03
光学检测
利用薄膜干涉现象检测光 学元件的表面质量、光学 薄膜的厚度和折射率等参 数。
光学信息处理
利用薄膜干涉现象实现光 学信息的调制、滤波和合 成等操作。
光学仪器
薄膜干涉现象用于制造各 种光学仪器，如干涉仪、 光谱仪和望远镜等。
02 等倾干涉原理
等倾干涉的概念
01
等倾干涉是指当平行光束入射到薄膜表面时，在等 倾角的位置上产生干涉现象。
实验设备
分束器
将激光分成反射和 透射光束。
观察装置
包括显微镜和屏幕， 用于观察干涉现象。
激光源
用于提供单色相干 光源。
薄膜样品
需要制备不同厚度 和折射率的薄膜样 品。
测量工具
用于测量薄膜厚度 和折射率。

Cn
e
B n2
e
sin2 r
2n
2ne
cos r
cos r
又由折射定律：
n sinr n1 sini
2n e cosr
光在界面反射时有
得：
2en cos
r
(0或
2
)
相位突变，则必须 考虑半波损失，加上
(2d
n2
n2 1
si n2
i
)
(0或
) 2
附加光程差
问题：什么情况下加附加光程差？
k2 l
第（k+1）级暗条纹
k 1 k0
Δe
k1 k2
ek
第k级条纹对应的厚度 ek
同一级条纹对应同一膜厚，
ek 1
(2k
k
1)
2n
第k级暗条纹
4n
明纹 (k 1,2 )
暗纹(k 0,1,2
)
故称为等厚条纹或等厚干涉
K=0，对应e=0，为劈尖边缘，叫做边缘暗条纹 ， k=1，e=/2n——第一级暗纹下面的薄膜厚度， e=/4n——第一级明纹下面的薄膜厚度……
sin 2n
太大条纹太密看不清
B. l ，白光照出彩条。
5、应用：
测波长：已知θ、n，测l可得λ 测折射率：已知θ、λ，测l可得 n
e ek1 ek 2n l ek1 ek
sin 2n
测微小角度：已知 n、λ，测l可得微小角度
测细小直径、厚度、微小变化 λ
平晶
n1
4、相邻明纹（或暗纹）间距
2ne
2
k (2k
k 1)
2
1,2,
明纹
k 0,1,2, 暗纹

清晰明亮，次极大处的条纹相
对越来越暗，甚至不被察觉。
光的干涉
N=2 N=3 N=4 N =10
N 很大
-2
-1
0
1
2
N 增大，主极大条纹变亮变窄，次极大数目变多而相对强度变小。
光的干涉
N=2 N=3 N=4 N =10 N 很大
N个相干线光源干涉条纹示意图
意义最大的是厚度均匀薄膜在无穷远处的等倾条纹 (equal inclination fringes)和厚度不均匀薄膜 表面的等厚条纹(equal thickness fringes) 。
光的干涉
肥皂泡和在平静水面上的油膜表面的彩色图样， 许多昆虫（蝉、蜻蜓）翅翼上所见的缤纷色彩 皆是薄膜前后表面反射光的干涉所致。
相应的相位差
光的干涉
相邻两光线在 P 点的相位差
设各光线在 P 点的振幅大小均为 用旋转矢量法求 N 个振动的合成振幅大小
先粗略了解 随
的变化概貌
同向叠加（主极大） 自行封闭
同向叠加（主极大）
同向叠加
自行封闭 位于相邻 自行封闭 两零值间
同向叠加
（主极大）
（次极大）
（主极大）
光的干涉
与
各旋转矢 量的垂直 平分线的 公共交点
光的干涉
完
光的干涉
光的干涉
备用资料
光的干涉
光的干涉
光的干涉
光的干涉
光的干涉
光的干涉
例6
光的干涉
例7
光的干涉
光的干涉
光的干涉
光的干涉
640 nm
4.80 mm 6.40 mm
4.00 m
光的干涉
光的干涉
光的干涉

⑶ 当i不变、d变，则d相同处出现同一条纹 —— 等厚干涉； 当i变、d不变，则i相同的入射光产生同一条纹 —— 等倾干涉；
⑷ 透射光 a'' 、b''间的光程差与. a' 、b'间的光程差相差λ / 2。
增透膜：
在透镜表面镀上折射率为n的透明薄膜，并
使n1<n<n2，波长为 λ 的入射光垂直入射。
解：未充液体时第10环的直径为：d10 2
劈尖：平行等间隔条纹
⑵ 牛顿环：
设单色光垂直入射（i = 0），n = 1
L2nd2 2kk12
明环 暗环
r 2 R 2 (R d ) 2 2 R d d 2 2 Rd
r 2Rd (L)R
2
C λ
R（很大）
r d
O
牛顿环仪
明环半径 暗环半径
r (k 1 )R
2
r kR
O点处：d = 0、 Δ L = λ /2 —→ .暗斑
解：
⑴ 由条纹突起的方向可判断是凹槽。
⑵ 由下图：
asin h bsin
2
sin h
a
sin
2b
解得： h a
b2
.
a b
b a
h
α dk
dk+1
h
例题4-11：
当牛顿环装置中的透镜与玻璃板间充以某种液体时，牛顿环中第 10个亮 环的直径由 1.40 cm 变为 1.27 cm ，求这种液体的折射率。
§4.3 薄膜干涉 （分振幅法）
1、光程差公式：
Ln(A C C)P n 1A B 2
2nAC n1AP siin2
2nd 2dsirn nsirn

《大学物理》
教师：
胡炳全
《大学物理》
教师：
胡炳全
L 2ne / 2 k
k 1对应的薄膜厚度最小
emin
emin

4n
无半波损失时,增反膜的 最小厚度:

2n
《大学物理》
教师：
胡炳全
增透膜的最小厚度与增反膜情况正好相反(如下表):
最小厚度 有半波损 无半波损 失 失 λ/4n λ/2n 增反膜
增透膜 λ/2n λ/4n
《大学物理》
教师：
胡炳全
第三节 薄膜干涉
一、薄膜干涉及其分类： 光线经过薄膜的两个 界面反射后在入射光一侧 发生的干涉,或透射光与 经过反射的透射光在入射 光的另一侧发生的干涉称 为薄膜干涉.前者反射光 (薄膜)干涉，后者叫透射 光(薄膜）干涉. 薄膜干涉发生的位置,可以 在薄膜的上下两个表面附近,也 可以在其它任何地方.通常我们 考虑的是发生在薄膜表面附近 的等厚干涉. P
由三角形AOO’，可得该处干涉的 光程差与半径r的关系为：
R ( R e) r
2 2
2
r e r e 2R 2R
2 2 2
nr L {0, / 2} R
干涉条纹一定是圆环，因为r相同， 厚度相同，光程差相同：
《大学物理》
教师：
胡炳全
•牛顿环干涉明纹和暗纹的半径（有半波损）
nr 由L / 2 k , 可得 : R
2
(2k 1) R r明 2n
nr 1 由L / 2 (k ) , 可得 : R 2
2
kR 空气中 r暗 kR n
牛顿环干涉 中心处为暗 纹（斑）

★ 结论：薄透镜不会引起各相干光之间的附加光程差。
20
万物之美 科学之理
目录
第一节 光源 光波 光的相干性 第二节 光波的叠加 光程与光程差 第三节 分波阵面干涉 第四节 分振幅干涉 第五节 迈克尔逊干涉仪 第六节 迈克尔逊干涉仪
第三节 分波阵面干涉
杨氏双缝干涉实验
实验现象
s1
S
s2
明条纹位置 明条纹位置 明条纹位置
42
第四节 分振幅干涉
43
第四节 分振幅干涉
练一练 观察 n=1.33 的薄油膜的反射光，它呈波长为 500nm 的绿光， 且这时法线和视线夹角 i=45o
求 （1）膜的最小厚度
i
（2）若垂直观察，此膜呈何种颜色
d
解 （1） 绿光干涉相长
数据代入（k=1）： （2） 垂直观察
深黄色
44
第四节 分振幅干涉
P
S1
r2 d
x
2
1
0
I
S2
D
1
x
2
25
第三节 分波阵面干涉
讨论
D、d 一定时， x 或 x
若用白光照射双缝，屏上中心明纹仍为白色，两侧对称分布各级紫内红 外的彩色条纹。更高级次的彩色条纹可能会发生重叠 。
0
1
2
3
0 1 23 4
中央明纹
3
2
1
0
1
2
3
26
第三节 分波阵面干涉 洛埃镜
M
S1 •
5
第一节 光源 光波 光的相干性
光波
1、颜色与光波
光色 波长(nm)
可
红
760~622
见
光 七

Hale Waihona Puke 光波在薄膜上的多次反射与折射
θ
tn
薄膜干涉的复杂性
• 仅仅从一个点光源发出的光波，经过薄膜不同表 面的多次反射就可以在各处进行干涉（非定域）
• 点光源为理想光源，且强度弱，不易观察
S
薄膜干涉的复杂性
• 实际为扩展光源发出的光波，可增强干涉视场强度
• 干涉条纹并非在整个空间可见，而只能在特定的区 域出现（定域干涉）
光波在薄膜上的多次反射与折射仅仅从一个点光源发出的光波经过薄膜不同表面的多次反射就可以在各处进行干涉非定域干涉条纹并非在整个空间可见而只能在特定的区域出现定域干涉所以要采用一定的方法或装置观察某一类光波的干涉两类典型的薄膜干涉一等倾干涉平行光波之间的干涉薄膜上下表面相互平行二等厚干涉光波在薄膜表面处的干涉薄膜上下表面不平行第一列反射光有半波损失而其他的反射光没有半波损失产生了附加相位等效于产生了半波损失
得第N条亮纹的角半径（半径对透镜中心所张开的角，入射角）：
i1N
=
1 n1
n2 Nλ
h
相应的干涉圆环半径：
rN = i1N f
相邻亮纹的角间距：
i1N
=
n2λ
2n12hi1N
相邻亮纹间距：
rN =i1N f
n1 i1 i1 n2 i2
j +1 j
δ i1 ∆i1
第j级亮条纹
λ
2n2h cos i2 = (2 j +1) 2
2n2h sin i2δi2 = λ / 2
δ i2
=
λ
4n2h sin i2
膜厚增大，条纹细锐
中心条纹没有周围细锐
条纹中心疏，周围密
2.6.2. 等厚干涉 （薄膜两表面不平行）

l

h
明纹中心
2. 干涉条件
暗纹中心
k 0,1,2
3. 特点
•劈尖干涉是等厚干涉 •劈尖的等厚干涉条纹是一系列等间距、明暗 相间的平行于棱边的直条纹。 •空气劈尖相邻明条纹对应的厚度差：
ek ek 1 h L l e / 2
4 .若劈尖间夹有折射率为 n 的介质，则：
e /(2n)
例8－3．如图所示，在折射率为1.50的 平板玻璃表面有一层厚度为300nm，折 射率为1.22的均匀透明油膜，用白光垂 直射向油膜，问： 1)哪些波长的可见光在反射光中产生 相长干涉? 2)若要使反射光中λ=550nm的光产生相 消干涉，油膜的最小厚度为多少? 解：(1)因反射光之间没有半波损失， 由垂直入射i=0，得反射光相长干涉的 条件为
劈尖相邻级次条纹对应的薄膜厚度差为膜内光波长的一半。 •薄膜厚度的测量
tan e / l

2l
应用
•薄膜厚度的测定
h L

2l
•测定光学元件表面的平整度
L
结论
2e / 2 k
明纹中心 暗纹中心
2e / 2 (2k 1) / 2 k 0,1,2

h b b

2a
得：h＝0.219 m
三、牛顿环
1. 实验装置
用平凸透镜凸球面所反射 的光和平镜上表面所反射 的光发生干涉，不同厚度 的等厚点的轨迹是以O为 圆心的一组同心圆。
T
S
M
O
N
2、干涉公式
2e / 2 k
k 1,2,3
明环中心
2e / 2 (2k 1) / 2 k 0,1,2,3 暗环中心

照像机对此波长反射小，可在照像机镜头上镀一层氟化镁MgF2 薄膜，已知氟化镁的折射率 n=1.38 ，玻璃的折射率n=1.55.
求:氟化镁薄膜的最小厚度. 解:两条反射光干涉减弱条件
r1
r2
2nd (2k 1) 2
增透膜的最小厚度
k 1,2,
d
550 d 100nm 4n 4 1.38
光线垂直入射
i 0
入射光
反射光1 反射光2
d
2k 2 2n2 d 2 （2k 1 ） 2
k 1,2, 相长干涉 k 1,2, 相消干涉
2
2k k 1,2, 相长干涉 2 2 2d n2 n12 sin 2 i 2 （2k 1 ） k 1,2, 相消干涉 2
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
例1(教材P19
例22.5)为测量一细金属丝的直径d，按
图办法形成空气劈尖，用单色光照射形成等厚干涉条纹， 用读数显微镜测出干涉明条纹的间距，就可以算出d。
已知单色光波长为589.3 nm，测量结果是：金属丝与劈
解:设空气的折射率为 n1 1.00 油膜和玻璃的折射率分别为 n2 1.30 和 n3 1.50
在油膜上下表面的反射光都有相位突变,所以, 0
反射光光程差干涉极小时,应有:
1 2en2 2k 1 k 2 2
7

设 1 500 nm 对应 k 级干涉极小,

高中物理光的干涉问题解析在高中物理学习中，光的干涉是一个重要的概念，也是考试中经常出现的题型之一。

干涉是指两束或多束光波相互叠加产生的现象，它可以解释许多光的特性和现象，如薄膜干涉、杨氏双缝干涉等。

本文将通过具体的例题，分析解决干涉问题的方法和技巧，帮助高中学生更好地理解和应用干涉概念。

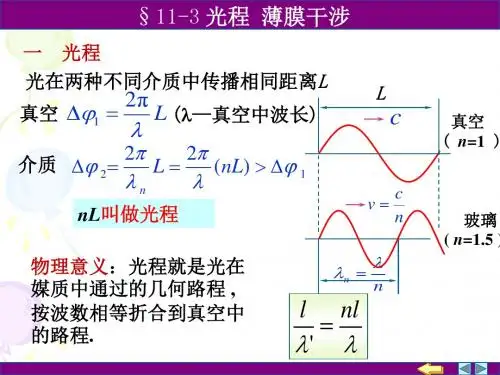
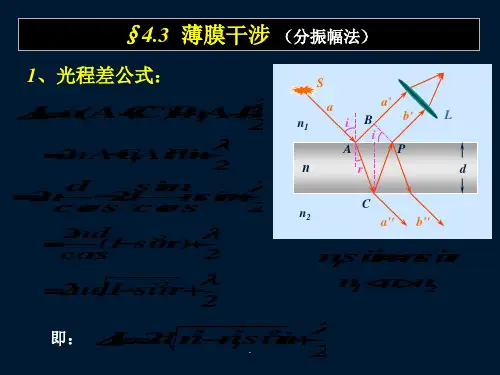
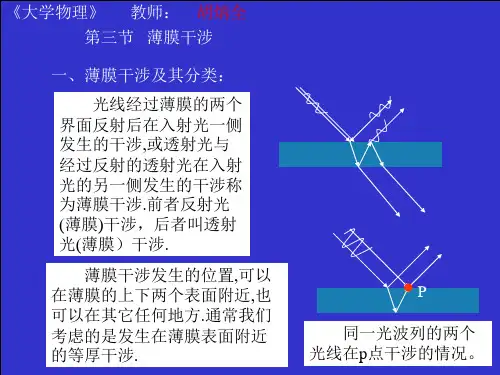
一、薄膜干涉问题薄膜干涉是光的干涉中的一个重要问题。

我们以一道光线从空气射入厚度为t的透明薄膜，然后射入介质为n的介质中，再从介质射入空气中。

这个过程中，光线会发生反射和折射，产生干涉现象。

下面我们通过一个例题来说明解决薄膜干涉问题的方法。

例题：一束波长为λ的光垂直射入厚度为t的空气膜，上下表面的折射率分别为n1和n2，已知n1>n2。

当n1t=λ/4时，求干涉条纹的间距。

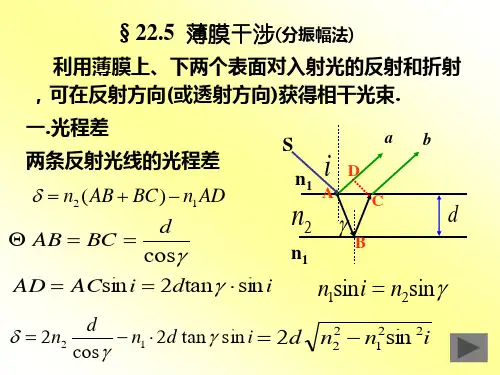
解析：根据薄膜干涉的条件，当光波从厚度为t的薄膜射出时，光程差为2nt。

而干涉条纹的间距与光程差有关，可以通过以下公式计算：间距d = λ / (2(n1-n2)cosθ)其中，θ为入射角。

在本题中，由于光是垂直射入薄膜，所以θ=0°，cosθ=1。

代入已知条件，我们可以得到：d = λ / (2(n1-n2))这样，我们就得到了干涉条纹的间距与波长、折射率之间的关系。

通过这个例题，我们可以看出，解决薄膜干涉问题的关键是确定光程差和干涉条纹的间距之间的关系，并运用相关公式进行计算。

二、杨氏双缝干涉问题杨氏双缝干涉是光的干涉中的另一个重要问题。

我们将一束光通过两个狭缝射入屏幕上，观察到一系列明暗相间的干涉条纹。

下面我们通过一个例题来说明解决杨氏双缝干涉问题的方法。

例题：两个狭缝间距为d，一束波长为λ的光垂直射入，屏幕离狭缝距离为D。

求第m级明条纹的角宽度。

解析：根据杨氏双缝干涉的条件，明条纹的角宽度可以通过以下公式计算：θ = λ / d其中，θ为角宽度。

在本题中，我们需要求解第m级明条纹的角宽度，可以通过以下公式计算：θm = mλ / d这样，我们就得到了第m级明条纹的角宽度与波长、狭缝间距之间的关系。

3、薄膜干涉的应用
（1）增透膜：在透镜、棱镜等光学元件的 表面涂有一层呈淡紫色的薄膜，增强透射光 强度，减少光的反射引起的损失。增透膜的 厚度为（ ）
透射光在薄膜中波长的1/4倍（ λ绿/4）
使薄膜前后两面的反射光的光程差为λ/2，
故反射光叠加后减弱
例、市场上有种灯具俗称"冷光灯"，用它照射物 品处产生的热效应大大降低，从而广泛地应用于博 物馆、商店等处。这种灯降低热效应的原因之一是 在灯泡后面放置的反光镜玻璃表面上镀一层薄膜 （例如氧化镁），这种膜能消除不镀膜时玻璃表面 反射回来的红外线热效应。以λ表示此红外线的波 长，则所镀膜的厚度最小应为：
三、薄膜干涉（光程差：薄膜厚度的2倍）
1、相干光源：薄膜前后两个表面的反射光
2、现象：单色光：明暗相间的单色条纹 白光：彩色条纹
例：用单色光照射肥皂薄膜时，发生光的干涉现象，这 时（AB） A、看到的干涉图样是明暗相间的条纹 B、从光源所在侧才能看到干涉图样 C、从光源的对侧才能看到干涉图样 D、从光源发出的光与肥皂膜表面反射的光发生干涉， 形成干涉图样
；一键测量仪/ 一键测量仪 ；
爬在树上，弄得满头满脸的都是乱扑扑的桃花瓣儿。等回到家，又总被母亲从衣 领里抖出一大把柔柔嫩嫩的粉红。啊，那个孩子呢？那个躺在小溪边打滚，直揉得小裙子上全是草汁的孩子呢？她隐藏到什么地方去了呢？ ⒅啊，春天多叫入迷惘啊！它究竟是怎么回事呢？是谁负责管理这 最初的一季呢？他想来应该是一种神奇的艺术家了，当他的神笔一挥，整个地球便美妙地缩小了，缩成了一束花球，缩成了一方小小的音乐匣子。他把光与色给了世界，把爱与笑给了人类。啊，春天，这样的魔季！ （选自《张晓风自选集》，有删改） 17．阅读全文，概括文中实写的两 幅主要画面。（4分） 答：18.请为第②节中加点词写一段赏析性批注。（4分） 山容已经不再是去秋的清瘦了，那白绒绒的芦花海也都退潮了。 批注： ? 19.结合语境，理解第⑧节画线句的深刻含意。（3分） 春天我们该到另一所学校去念书的。 答：20.文章标题为“魔季”，为什么 却浓墨重彩地描写了一个小女孩？（5分） 答： ? 21.第⑥节用了十个问号，可是读起来一点也不显得单调，反而别有韵味。仔细阅读这节文字，说说这样表达的作用，并分析其中蕴含的丰富情感。（6分） 答：代谢：17．（1）绿色的谷和清澈涧水里的花瓣。（2）我与小山居者凯凯相 遇的画面。【解析】这题考查概括文本的能力，注意审题，要求概括的是实写的画面，一个是大自然的画面，一个是人在自然中的画面。 18.“清瘦”这里用来形容去年的秋天，是运用了拟人的修辞手法，生动形象地写出了秋天的山之萧瑟景象，从而反衬出春天山上的丰盛之美。“退潮” 这里是写白绒绒的芦花海，运用了比喻的修辞手法，生动形象地写出了秋天时芦花繁茂和美丽，像白色的浪花一般，而到了春天，满山是绿色，通过这样的颜色对比，更加突出了作者对春天的喜爱。【解析】这题考查的是对修辞的赏析能力。结合上下文理解修辞在这里所起到的表达效果 即可。 19．春天的时候我们人类应该到大自然中去学习。? 【解析】这题考查的是句子的含义。通过联系上下文把握句子里比喻词的深层含义。“另一所学校”在文中指的是大自然。 20．（1）通过小女孩凯凯对春的反应和大自然景物的照应来衬托出春的美妙。（2）通过小女孩的话， 自然引出作者的观点“春天我们该到另一所学校去念书的”。（3）小女孩的纯朴快乐就像春天一样美好。（4）小女孩的年纪就正处在人生中的春天。（5）小女孩让作者想起了自己小时候春天的故事。【解析】解答这个题目，要结合文章内容和作者的情感来回答，理解小女孩和景物之 间的关系，小女孩和作者情感之间的关系，小女孩自身的象征含义。 21．（1）运用了多个疑问句和反问句。多个疑问句连用表现了作者联想的过程，构成了悬念，使读者被带领吸引着往下读，引出了下文写童年自己，表现了作者对春天的无比喜爱之情。（2）紧接着是几个反问句，回 忆了童年对自己春天的生活，非常强烈地表达了对江南的怀念，对童年的追忆，对母亲的爱。（3）最后又是两个疑问句，表现了作者对童年不再的怅然若失之情。? 【解析】十个问句，较多，可以根据内容和情感的不同进行划分，逐个解答，切忌眉毛胡子一把抓，不去条分缕析，就会 漏掉要点失分。 （2017山东济宁）（二）阅读下面的文章，完成1-20题。 （15分） 胡 记 面馆 马苏玥 （1）①胡记面馆，是小城东头最有名的面馆，胡家世代经营着小城老街偏东头的面馆子，靠着祖上流传下来的古法做面发家，子孙代代相传。用古法精心配制出来的面细润筋道、清 新爽口，吃过的人没有不夸赞的。? （2）老街人看到这代胡记的掌勺兼老板老胡都笑嘻嘻地打招呼：“老胡，多做一碗吧，馋面喽。”老胡也笑：“三六九，年年有，祖宗的老规矩俺可不敢改了!饿饿吧，明天再来。”? （3）胡记面做起来可不容易!﹣年里下麦子的时候，挑熟好的麦捆 回家，人推着石磨细细地磨，这样面粉老到细腻。面是在头天晚上和的，先把面用水一裹，搓成块块，再加碱醒面，碱要讲纯度，不能太杂。面要醒到苦里发甜，味不对就弃面重醒，醒好的面用湿布包着放一晚，第二天拉的时候，面就筋道，任人拉扭。这一步步说着简单，做起来复杂麻 烦，可胡家人从来不嫌麻烦，因为，少或改了步骤，面就不如之前鲜嫩了。? （4）老胡有个独子﹣﹣胡良，娃娃脑子灵光，什么东西都一学即会，老胡很早就让儿子学手艺。 （5）胡良学着老爹磨面、和面、拉面。揪起一拳头大的面，搓成匀粗的长条，再压平扁，用快力划上几条长口， 一手抓起一头面，用大臂的匀力扯面，双臂翼张于胸，“啪”的一声合起面上下一抖，再拉。统共拉八次。完后用手托着面条，快速削去面头，左右一甩，把身子一仰，手里的面顺着就到了灶上的沸水里。然后伸双长筷，搅几下捞到一边盛高汤的瓷碗里。做好的面乍一瞧，就像是条条羊 脂玉浸在汤里。胡良的手艺比他爹还要强一分。? （6）胡家面做起来又费时又费力，祖上说，烹小鲜如治大国，一日卖两顿，一顿36碗上等面，就保得胡记不衰。胡家祖宗规定的数量不光是为了讨个吉利，也是经过实践得来的，一个人不急不忙，一天顶好才能做出72碗上等面来。胡记 面全在磨、和、拉三字里，一步也少不得，缺不得，减不得啊! （7）祖宗的规矩，老胡从没坏过。一天72碗上等面，不多不少。? （8）这天晚上，胡良正和面，皱眉跟老胡说：“爸，咱家一天多做几碗，用厂里出的面粉，雇个人和面，改改老法子，就快了。我试过，那面模样一点儿不 差，味道也不差太多。”? （9）“什么混话，那样的面还叫胡记吗？”老胡一听，气得拍了下桌子，“胡记面贵在每根都包含着厨子的心血，是花过心思的，这些可全藏在一步步流程规矩中，老祖宗的法子不能改啊!”? （10）“什么年代了，有胡氏这块招牌，老法子稍变有什么嘛!” 胡良不服气。 （11）“这哪是变法子，这是砸牌子，招牌砸了，往后拿什么做生意？”? （12）胡良没听，在城中央偏东的地方开了家分店。 （13）往后老街人从城里回来，看着老胡：“小胡开了家分店哩，生意红红火火，一天卖几百碗，儿子赶上老子喽。”? （14）老胡不再笑了， 只是愤愤抚手，频频叹气。 （15）有个城里谋生计的老街人有回点了碗胡记分店面，才吃了一口，就搁筷了，咂咂嘴：“不比老街的胡记呦，少了点儿筋道味儿。”周围正大快朵颐的食客皆惊奇。 （16）有好面的食客闻讯赶往老街。 （17）老街这边，胡良一走，店就留了老胡一人， 老胡依然按规矩，一天72碗上等精面，不多不少。食客大呼：“极妙!”陶然于老街胡记。渐渐消息传开，胡良的生意淡了。大凡吃了城中胡记的，都来了老街，而吃了老街的，却再没回到城中胡记。胡良开始入不敷出了。? （18）胡良回了老街。 （19）老胡看见儿子，也不说话，只管 做面。胡良吃了口老胡的面，想了想城中面馆的面，矮了头。 （20）胡良又开始做面了，一天72碗，跟他爹一样。胡记名声越传越远，一碗面是别家三四倍价钱，但小面馆生意仍然红火，有本地、外地，甚至还有别国的人。老街东头，胡记门外经常排长龙队。 （21）那年老胡病了，胡 良在跟前，老胡说：“别说爸迂腐，不懂变通，爸咋不知道赚钱？爸守的不是老规矩，不是这胡记招牌，而是这面的品质味道。做生意不用好货，待时间久了，谁买你的账？要想做好生意，就得本本分分，不搞噱头。做面和做人、做事一样，得守好底线，脚踏实地，才能摘到星星揽到月 亮。”胡良泪汪汪地听。 （22）“再去给老子做碗面吧!” （23）胡良端着面回来，老胡捧在手里，对着光瞧了瞧，面条细若发丝，色泽细亮，挑起一筷子，吸上一口，面质轻柔，鲜香可口。老胡眯着眼，长嘘口气，“就是这个样。”随即倒在了一边，手中那碗却端端正正，滴汤不 洒。? （选自《齐鲁晚报》2017-03-02，有删改）? 17.文章第②段有何作用？（4分） 答： 【代谢】承接上文表现胡记面馆口碑好，引出下文对胡记面馆工艺精细的描写； 突出了老胡坚守规矩的形象特点；为后文写老胡反对破坏规矩做铺垫。（每点2分，答出两点即可） 【解析】本 题考查段落作用的分析．解答此题一般从结构与内容两方面入手。从内容上看，这段表现了胡记面馆的数量有限，老胡对祖宗的规矩的遵守；从结构上看，引出下文胡良不遵守祖辈规矩的情节，推动故事情节的发展。 18.赏析第⑤段画线句子的表达效果。（3分） 答：? 【代谢】18.示 例：（1）运用一系列动词，详写拉面过程，表现了胡良手艺高超，做面工艺精细。（2）多用短句，简洁明快，表现了胡良动作干净利落，手艺精湛。 （指出分析角度1分，点明效果2分） 【解析】本题考查句子的赏析。解答此题可以从人物动作描写来分析。句子主要描写了胡记面制作 的过程，从一连串的动作可以看出，面的制作复杂，也正因此才会受到人们的欢迎。 19.小说主要运用了对比手法，试举一例分析。（4分） 答：?【代谢】示例： （1）胡良开分店前期生意红火，后来入不敷出，回归传统后生意仍然红火，前后对比，使小说情节跌宕起伏，也凸显了主 题。 （2）胡良破坏规矩经营失败，老胡坚守优良传统生意兴隆，两个人物形成对比，暗示了主题。 （举例2分，分析作用2分。分析合理即可。） 【解析】本题考查写作手法的理解与分析。对比手法：是把具有明显差异、矛盾和对立的双方安排在一起，进行对照比较的表现手法，通过 比较，突出事物的特点，更好地表现文章主题。文中的对比有：老胡对祖训的遵守与胡良对祖训的弃之不顾；食客对老胡与胡良面的夸赞；胡良在开分店前后的态度等，表现出做生意要厚道，要以真实的手艺来博得顾客的赞誉。 20.分析下面句子的含义。 （4分）老胡眯着眼，长嘘口气， “就是这个样。” 答：?【代谢】老胡对儿子的手艺感到欣慰；希望儿子守好底线做人，脚踏实地做事。 （欣慰2分，希望2分） 【解析】本题考查句子含义的理解。题目所给的句子正是全文点明主旨的句子，从老胡对祖训的坚守，胡良生意的失败，可以知道这句话的含义是做生意就得 守本分，要诚信。 【分析】本文可分为四个部分：第一部分（1～3），介绍胡记面馆的特色；第二部分（4～11），写胡良央求父亲每天多做些面，能挣更多的钱，遭到老胡的拒绝；

为n的透明介质膜上，要使透射光得到加强，薄膜
的厚度最少应为（ Ａ）
A，λ/4n； B，λ/2n； C，λ/4； D，λ/2
牛顿环
干涉图样：中央疏边沿密的同心圆环
照相机：
因为人的视觉最敏感的色光为绿光，所以增透膜的
厚度为绿光在增透膜中波长的1/4。以增大绿光的
透射强度。 因为红光与紫光反射强度大，所以照相机的镜头常 呈淡紫色或蓝色
3、高反射膜（增反膜）
薄膜厚度
d 2
2
防紫外线眼镜 路标
高反射膜
1、有关光学仪器上镜头的增透膜，下列说法正确的
是：（ ＡＤ）
回答下图中P点和M点对应的位置是凹陷还是凸起?
薄膜厚度
d 2
4
设增透膜的折射率为n，光在
真空中的波长为λ1，在介质中 的波长为 Nhomakorabea22
1
n
原理：当薄膜的厚度是入射光在 薄膜中波长的１∕４时，在薄膜 的两个面上的反射光，光程差恰 好等于半波长，因而相互抵消， 达到减小反射光，增大透射光的 作用
增透膜
A．增透膜是为了减少光的反射损失而增强透光的强 度； B．增透膜的厚度等于入射光在真空中波长的λ/4； C．增透膜的厚度等于入射光在薄膜中波长的λ/4； D．因为增透膜厚度一般选适合绿光反射相互抵消的 厚度，红光紫光反射不能完全抵消的厚度，所以涂 有增透膜的镜头呈淡紫色。
7、将波长为λ的单色光从空气垂直入射到折射率
薄膜干涉中的色散：
1、薄膜干涉实验：
1）现象：水平明暗相间条纹
2)现象解释：
⑴当 2d k 时，出现亮条纹 ⑵当 2d 2k 1时2 ，出现暗条纹
用白光照射薄膜会出现什么现象？
1)光在油膜上下表面反射后干涉 2)昆虫的翅膀呈彩色 3)某些金属的表面呈彩色 4)照相机的镀膜镜头是有颜色的