下载文档原格式
薄膜干涉光程差公式高中薄膜干涉光程差公式 在物理学中，薄膜干涉是涉及光的波动性质的一种现象。
光程差是用来描述光通过不同介质或空气中传播时所经过的距离差。
薄膜干涉光程差公式是用来计算不同介质或空气中的光程差的公式。
本文将详细介绍薄膜干涉光程差公式的推导和应用。
第一段：什么是薄膜干涉 薄膜干涉指的是光在透明材料表面反射和折射时发生的干涉现象。
当光线通过一个薄膜时，会发生反射和折射，而这两束光线再次相遇时会产生干涉。
这种干涉现象可以用于解释一些自然界或实验室中观察到的颜色变化现象，例如气泡的彩色、油膜上的彩色等。
第二段：什么是光程差 光程差是指光线从一个点到另一个点所经过的路径长度差。
当光线通过一个介质或空气时，会因为介质的折射率不同而导致光程差的发生。
光程差是薄膜干涉现象中的一个重要参数，它决定了干涉条纹的样式和颜色。
第三段：薄膜干涉光程差公式的推导 薄膜干涉光程差公式可以通过菲涅尔公式和折射定律来推导。
菲涅尔公式描述了光在介质的折射和反射过程，折射定律则是描述光在不同介质中传播时的折射规律。
推导过程如下： 假设有一薄膜，其上方为介质1，下方为介质2。
光线从空气（介质1）射入到薄膜（介质2）的表面，首先发生反射，根据反射定律可知反射角等于入射角。
即：θ1 = θr。
接下来，光线从薄膜（介质2）射入到空气（介质1），发生折射。
根据折射定律可知折射角与入射角和折射率的乘积之比相等。
即：θr = θ2 / n2。
根据几何关系可知：θ1 + θ2 = φ，其中φ为干涉条纹的相位差。
代入上述公式和几何关系中可得：θ1 = (n2 / n1) * φ通过一个周期的干涉条纹相位差为2π，因此有：φ = 2π / m，其中m为干涉条纹的级数。
将上述公式代入θ1的公式中可得：θ1 = (n2 / n1) * (2π / m)结合菲涅尔公式和折射定律，可得到薄膜干涉光程差公式： δ = 2 * d * (n2 / λ) * cos(θ1) 其中，δ为光程差，d为薄膜的厚度，n2为介质2的折射率，λ为入射光的波长，θ1为入射角。
薄膜干涉光程差公式高中
【最新版】
目录
1.薄膜干涉光程差公式的背景和基本概念
2.薄膜干涉光程差公式的推导和理解
3.薄膜干涉光程差公式在实际应用中的意义
4.薄膜干涉光程差公式的扩展和深化理解
正文
薄膜干涉光程差公式是光学中的一个重要公式，它描述了薄膜干涉现象中光程差的计算方法。
在薄膜干涉中，由于光的波动性和薄膜的厚度，光在薄膜的前后表面反射后会产生干涉，形成明暗相间的干涉条纹。
而薄膜干涉光程差公式就是描述这种干涉条纹的关键公式。
一、薄膜干涉光程差公式的背景和基本概念
薄膜干涉光程差公式的推导源于光的波动性和薄膜的厚度。
在薄膜干涉中，光在薄膜的前后表面反射后会产生干涉，形成明暗相间的干涉条纹。
这种干涉是由光的相位差引起的，而光的相位差又可以通过光程差来描述。
二、薄膜干涉光程差公式的推导和理解
薄膜干涉光程差公式可以描述为：δ = (2ne + λ/2)d，其中n是薄膜的折射率，e是薄膜的厚度，λ是光的波长，d是薄膜的厚度。
这个公
式的推导过程比较复杂，需要考虑光的折射、反射和干涉等多种因素。
三、薄膜干涉光程差公式在实际应用中的意义
薄膜干涉光程差公式在实际应用中非常重要，它可以用来分析和计算薄膜干涉的条纹，以及条纹的亮度和颜色等特征。
同时，薄膜干涉光程差公式也可以用来制作各种光学元件，如减反射膜和干涉滤光片等。
四、薄膜干涉光程差公式的扩展和深化理解
在实际应用中，薄膜干涉光程差公式需要考虑一些特殊情况，如薄膜的厚度不等、光的波长不等等。
此外，薄膜干涉光程差公式还可以和其他光学公式结合起来，深化对光学现象的理解。
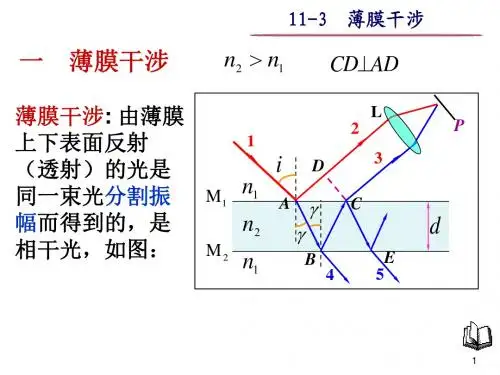
薄膜干涉的原理及应用薄膜干涉是指光线在两个平行的透明介质界面之间传播时发生的干涉现象。
薄膜干涉的原理主要有两种，一种是取决于光线经过薄膜时的反射和折射，另一种是取决于薄膜上存在的厚度变化。
首先，光线经过薄膜时的反射和折射产生干涉是薄膜干涉的一种原理。
当入射光线照射到薄膜上时，一部分光线被薄膜上的介质反射，一部分光线经过薄膜后折射出去。
由于折射率的差异，光线的相位发生变化，产生了干涉现象。
根据不同的入射角度和薄膜的厚度，干涉的结果有时是增强，有时是消减。
也就是说，入射光线经过薄膜干涉后，会出现明暗相间的干涉条纹。
其次，薄膜上存在的厚度变化也会导致光线的干涉现象。
当薄膜具有不均匀的厚度分布时，入射光线在不同位置的薄膜上经过不同的光程，从而产生干涉现象。
这种干涉称为厚度干涉，通过观察干涉条纹的形态可以获取薄膜的厚度信息。
薄膜干涉具有许多应用。
以下是几个常见的应用：1.薄膜干涉可以用于制造薄膜光学器件，如光学镀膜和光学滤光片。
通过选择适当的薄膜材料和调节厚度，可以实现对特定波长光的反射或透射。
这些器件在摄影、显示器、激光技术等领域中得到了广泛应用。
2.薄膜干涉在非破坏性测试技术中起着重要作用。
通过测量干涉条纹的变化，可以获取材料的厚度、表面形貌、应力等信息，从而判断材料的质量和性能。
3.薄膜干涉还可以用于生物医学领域的光学显微镜。
通过将样本置于薄膜上，当入射光通过样本和薄膜时，会发生干涉现象。
通过观察干涉条纹的形态和变化，可以获得有关样本的信息，如细胞的形态、结构和运动等。
4.薄膜干涉还可以应用于材料的质量控制和检测。
通过测量干涉条纹的变化，可以判断材料的化学成分、密度、厚度等，从而实现对材料质量的检测和控制。
总之，薄膜干涉是光学中一种重要的现象，其原理包括光线的反射和折射产生的干涉以及薄膜的厚度变化引起的干涉。
薄膜干涉具有广泛的应用，包括光学器件制造、非破坏性测试、生物医学等领域。
通过利用薄膜干涉的原理，可以实现对材料性能和质量的检测和控制。
薄膜的干涉的原理及应用一、薄膜干涉的基本概念薄膜干涉是指光波在经过透明薄膜时发生的干涉现象。
薄膜是一种在物体表面上有一定厚度的透明材料层。
当光波通过薄膜时，部分光波会被反射，而部分光波会被折射。
这两部分光波在空间中叠加形成干涉。
薄膜干涉现象是由于光的波动性和光在不同介质中传播速度不同的性质所引起的。
主要的原理是反射干涉和折射干涉。
二、薄膜干涉的原理2.1 反射干涉当一束光波垂直入射到薄膜上时，部分光波被反射，部分光波被折射。
反射光波和折射光波之间会发生干涉现象，形成反射干涉。
反射干涉的原理可以用光程差来解释。
光程差是指光波从光源到达观察者的路径长度差。
当反射的两束光波的光程差是波长的整数倍时，它们会相干叠加，形成明暗相间的干涉条纹。
2.2 折射干涉当光波从一个折射率较高的介质进入到一个折射率较低的介质中时，光波会发生折射。
在这个过程中，反射和透射的光波之间也会发生干涉。
折射干涉的原理与反射干涉类似，都是由光程差引起的。
当折射的两束光波的光程差是波长的整数倍时，它们会相干叠加，形成干涉条纹。
三、薄膜干涉的应用薄膜干涉在许多领域中有着广泛的应用，下面列举了几个主要的应用：3.1 光学镀膜薄膜干涉在光学镀膜中有着重要的应用。
通过在光学元件的表面上镀上特定的薄膜，可以改变光学元件的反射和透射特性。
利用薄膜的干涉效应，可以实现对特定波长的光的反射和透射的选择性增强或减弱，从而改善光学元件的性能。
3.2 惠斯托克森干涉仪惠斯托克森干涉仪是一种基于薄膜干涉原理的光学仪器。
它由两个平行的透明薄膜组成，在光路中产生干涉现象。
通过观察干涉条纹的变化，可以测量物体的形状、厚度和折射率等参数。
3.3 光学薄膜滤波器光学薄膜滤波器利用薄膜干涉的原理，可以选择性地透过或反射特定波长的光。
这种滤波器在光学传感器、摄像机、光学仪器等领域中广泛应用，用于分离和选择特定的光谱成分。
3.4 光膜干涉显示技术光膜干涉显示技术利用薄膜的干涉效应，在显示屏上产生出明亮、清晰的图像。
光的干涉与薄膜干涉实验光的干涉和薄膜干涉是光学实验中常见的现象，它们揭示了光的波动性质和光的干涉规律。
通过这两个实验，我们可以更好地理解光的行为和性质，以及应用于实际生活中的相关技术。
一、光的干涉实验光的干涉是指两束或多束光相互叠加形成干涉条纹的现象。
这种现象可以通过杨氏双缝干涉实验来观察和解释。
在光的干涉实验中，我们需要一个光源、一块可透光的屏幕和一对缝。
首先，我们将光源放置在一定的位置上，让光通过一个狭缝，形成一个细而直的光线。
然后，我们在透光屏的一端设置两个狭缝，光线通过这两个狭缝后形成两束光，并在透光屏的另一端投射到屏幕上。
当两束光线在屏幕上相遇时，它们会相互干涉并产生交替出现的亮暗条纹，也称为干涉条纹。
这些条纹的形状和间距取决于两束光线之间的相位差。
干涉条纹的出现可以用干涉现象的两种探测方法来解释：波的干涉和波的相长相消。
波的干涉是指两束光相遇时，波峰与波峰相重叠形成增强干涉，波峰与波谷相重叠形成减弱干涉。
而波的相长相消则是指两束光相差半波长或整波长时，波峰和波峰相长形成增强干涉，波峰和波谷相消形成减弱干涉。
通过观察和测量干涉条纹的特性，我们可以计算出两束光线之间的相位差，从而推导出光的波长和实际中的应用。
光的干涉实验在光学技术和科学研究中有着广泛的应用，例如激光技术、显微镜和干涉仪器等。
二、薄膜干涉实验薄膜干涉是指光线通过薄膜表面时，由于不同介质的折射率引起的光程差而产生干涉现象。
这种现象可以通过牛顿环干涉实验来观察和解释。
在薄膜干涉实验中，我们需要一个透明的非金属薄膜，如硬币反射面上的氧化层，和一个平坦的玻璃片。
首先，我们将玻璃片放置在硬币的反射面上，形成一个薄膜。
然后，从顶部照射一束光线，光线穿过玻璃片并通过薄膜，再次射出。
当光线经过薄膜时，根据不同介质的折射率，会产生不同的光程差。
光从薄膜表面射出后，会与反射的光线相干并产生干涉条纹。
通过观察这些干涉条纹的形状和颜色，我们可以判断薄膜的厚度和折射率。
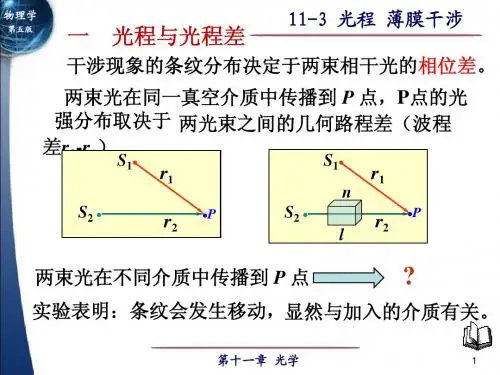
薄膜干涉光程差公式高中摘要：一、薄膜干涉光程差公式简介- 薄膜干涉光程差公式定义- 公式中各参数含义及物理意义二、薄膜干涉光程差公式推导- 薄膜干涉光程差公式推导过程- 注意要点及难点解析三、薄膜干涉光程差公式应用- 薄膜干涉在实际应用中的案例- 薄膜干涉光程差公式在案例中的应用四、总结与展望- 对薄膜干涉光程差公式的总结- 对未来薄膜干涉光程差公式的展望正文：一、薄膜干涉光程差公式简介薄膜干涉光程差公式，是描述光线在薄膜上下表面反射后，形成的干涉现象中，两束相干光之间的光程差与薄膜厚度、折射率等参数之间的关系公式。
它对于理解薄膜干涉现象、预测干涉条纹的分布以及进行薄膜厚度等参数的测量具有重要意义。
二、薄膜干涉光程差公式推导薄膜干涉光程差公式的推导过程涉及到一些光学基础知识，如光的折射、反射以及相干光的干涉等。
具体的推导过程如下：首先，假设光线在薄膜上下表面分别发生折射角为i和r的反射，光线在薄膜内部的传播距离为d，薄膜厚度为e。
根据光的折射定律，可以得到：1 * sin(i) = n2 * sin(r)其中，n1和n2分别为空气和薄膜的折射率。
接下来，考虑光线在薄膜上下表面反射后的光程差。
根据薄膜干涉的原理，光线在薄膜上下表面的反射光程差为2e，而在薄膜内部的传播光程差为d。
因此，总的光程差为2ne + λ/2，其中λ为光的波长。
最后，根据相干光干涉的原理，两束相干光之间的光程差应等于整数倍的波长，即2ne + λ/2 = m * λ，其中m为整数。
将上述两式联立，可以解得：e = (m * λ - λ/2) / 2n这就是薄膜干涉光程差公式。
三、薄膜干涉光程差公式应用薄膜干涉光程差公式在实际应用中有着广泛的应用，如薄膜厚度测量、光学薄膜设计等。
以下是一个具体的案例：在薄膜厚度测量中，假设我们已知光的波长为λ，折射率为n，以及干涉条纹的级次m。
通过测量干涉条纹的间距，可以得到：Δy = λ/m结合薄膜干涉光程差公式，可以求得薄膜厚度：e = (m * λ - λ/2) / 2n从而实现薄膜厚度的精确测量。
