当前位置：文档之家 › 第2节-光程差—薄膜干涉.

第2节-光程差—薄膜干涉.

  • 格式：ppt
  • 大小：858.50 KB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

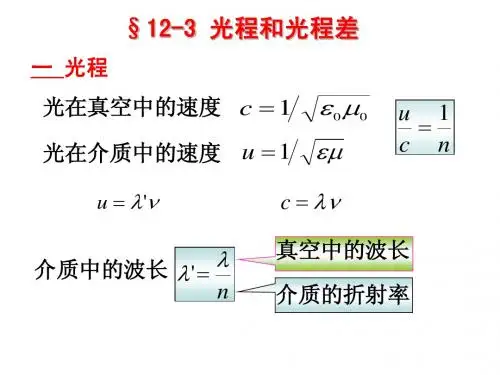
大学物理学之光程_薄膜干涉

大学物理学之光程_薄膜干涉

M
2dn2 cos / 2
N
2e n n sin i
2 2 2 1 2

2
（a) 干涉条纹的级次K仅与
倾角i有关，点光源S发出的 光线中，具有同一倾角的 反射光线会聚干涉，形成 同一级次圆环形干涉条纹 ，称为等倾干涉条纹。 (b) 对于不同倾角的光入射： 入射角 i 越小，光程差越 大，条纹越在中心。 条纹中心处，入射角i=0
第十一章 光学
16
3. 平行平面 膜干涉的应用
增透膜----利用薄膜上、下表面反射光的光程差符合相消 干涉条件来减少反射，从而使透射增强。
增反膜----利用薄膜上、下表面反射光的光程差满足相长 干涉，因此反射光因干涉而加强。
（1）增透膜(dark film)： 在折射率为 n1 的媒质表面 镀一层厚度为e的透明的折 射率为 n ，如果：
2 2 2 1 2

2
加强 减弱
( k 0,1,2,)
P
2
n1
i

D
对同样的入射光来说，当 反射方向干涉加强时，在 透射方向就干涉减弱。
n2
M2
A B 4
d
E 5
Δt 2d n n sin i
2 2 2 1 2
n1
透射光干涉条纹和反射光干涉条纹互补
物理学
第五版
11-3 光程 薄膜干涉
§12-3 光程和光程差
一 光程 光在真空中的速度 c 1 光在介质中的速度 u 1
u '
0 0

u 1 c n
c
介质中的波长 ' n
真空中的波长 介质的折射率
物理学

薄膜干涉光程差公式高中

薄膜干涉光程差公式高中

薄膜干涉光程差公式高中薄膜干涉光程差公式 在物理学中，薄膜干涉是涉及光的波动性质的一种现象。

光程差是用来描述光通过不同介质或空气中传播时所经过的距离差。

薄膜干涉光程差公式是用来计算不同介质或空气中的光程差的公式。

本文将详细介绍薄膜干涉光程差公式的推导和应用。

第一段：什么是薄膜干涉 薄膜干涉指的是光在透明材料表面反射和折射时发生的干涉现象。

当光线通过一个薄膜时，会发生反射和折射，而这两束光线再次相遇时会产生干涉。

这种干涉现象可以用于解释一些自然界或实验室中观察到的颜色变化现象，例如气泡的彩色、油膜上的彩色等。

第二段：什么是光程差 光程差是指光线从一个点到另一个点所经过的路径长度差。

当光线通过一个介质或空气时，会因为介质的折射率不同而导致光程差的发生。

光程差是薄膜干涉现象中的一个重要参数，它决定了干涉条纹的样式和颜色。

第三段：薄膜干涉光程差公式的推导 薄膜干涉光程差公式可以通过菲涅尔公式和折射定律来推导。

菲涅尔公式描述了光在介质的折射和反射过程，折射定律则是描述光在不同介质中传播时的折射规律。

推导过程如下： 假设有一薄膜，其上方为介质1，下方为介质2。

光线从空气（介质1）射入到薄膜（介质2）的表面，首先发生反射，根据反射定律可知反射角等于入射角。

即：θ1 = θr。

接下来，光线从薄膜（介质2）射入到空气（介质1），发生折射。

根据折射定律可知折射角与入射角和折射率的乘积之比相等。

即：θr = θ2 / n2。

根据几何关系可知：θ1 + θ2 = φ，其中φ为干涉条纹的相位差。

代入上述公式和几何关系中可得：θ1 = (n2 / n1) * φ通过一个周期的干涉条纹相位差为2π，因此有：φ = 2π / m，其中m为干涉条纹的级数。

将上述公式代入θ1的公式中可得：θ1 = (n2 / n1) * (2π / m)结合菲涅尔公式和折射定律，可得到薄膜干涉光程差公式： δ = 2 * d * (n2 / λ) * cos(θ1) 其中，δ为光程差，d为薄膜的厚度，n2为介质2的折射率，λ为入射光的波长，θ1为入射角。

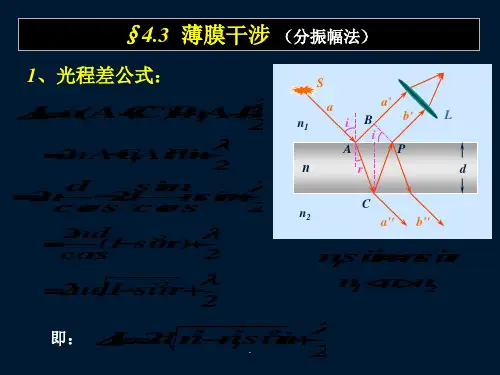
薄膜干涉 讲解

薄膜干涉 讲解

⑶ 当i不变、d变，则d相同处出现同一条纹 —— 等厚干涉； 当i变、d不变，则i相同的入射光产生同一条纹 —— 等倾干涉；
⑷ 透射光 a'' 、b''间的光程差与. a' 、b'间的光程差相差λ / 2。
增透膜：
在透镜表面镀上折射率为n的透明薄膜，并
使n1<n<n2，波长为 λ 的入射光垂直入射。
解：未充液体时第10环的直径为：d10 2
劈尖：平行等间隔条纹
⑵ 牛顿环：
设单色光垂直入射（i = 0），n = 1
L2nd2 2kk12
明环 暗环
r 2 R 2 (R d ) 2 2 R d d 2 2 Rd
r 2Rd (L)R
2
C λ
R（很大）
r d
O
牛顿环仪
明环半径 暗环半径
r (k 1 )R
2
r kR
O点处：d = 0、 Δ L = λ /2 —→ .暗斑
解：
⑴ 由条纹突起的方向可判断是凹槽。
⑵ 由下图：
asin h bsin
2
sin h
a
sin
2b
解得： h a
b2
.
a b
b a
h
α dk
dk+1
h
例题4-11：
当牛顿环装置中的透镜与玻璃板间充以某种液体时，牛顿环中第 10个亮 环的直径由 1.40 cm 变为 1.27 cm ，求这种液体的折射率。
§4.3 薄膜干涉 （分振幅法）
1、光程差公式：
Ln(A C C)P n 1A B 2
2nAC n1AP siin2
2nd 2dsirn nsirn

薄膜干涉的光程差

薄膜干涉的光程差

薄膜干涉的光程差
薄膜干涉的光程差是由两相干光在薄膜上下表面反射（或折射）而形成的。

光程差公式为：Δ=2ndcos(θt)±λ/2。

其中，n为薄膜的折射率，d为入射点的薄膜厚度，θt为薄膜内的折射角，±λ/2 是由于两束相干光在性质不同的两个界面（一个是光疏-光密界面，另一是光密-光疏界面）上反射而引起的附加光程差。

当光垂直入射到薄膜时，即入射角为0°时，光程差为半个波长，因此称为半波损失。

薄膜干涉原理广泛应用于光学表面的检验、微小的角度或线度的精密测量、减反射膜和干涉滤光片的制备等。

比较简单的薄膜干涉有两种，一种称做等厚干涉，这是由平行光入射到厚度变化均匀、折射率均匀的薄膜上、下表面而形成的干涉条纹。

薄膜光程差相同的地方形成同条干涉条纹，故称等厚干涉。

另一种称做等倾干涉，当不同倾角的光入射到折射率均匀，上、下表面平行的薄膜上时，同一倾角的光经上、下表面反射(或折射)后相遇形成同一条干涉条纹，不同的干涉明纹或片间的空气层就形成空气薄膜。

用水银灯或纳灯作为光源，就可以观察到薄膜干涉现象。

第2节_光程差—薄膜干涉

第2节_光程差—薄膜干涉

薄膜干涉的原理
第三章
薄膜干涉的概念
薄膜干涉的定义 薄膜干涉的原理 薄膜干涉的分类 薄膜干涉的应用
薄膜干涉的原理
薄膜干涉的定义： 指光在薄膜的两 个表面反射后叠 加产生的干涉现 象。
薄膜干涉的形成： 当光入射到薄膜 上时，一部分光 在薄膜的上表面 反射，另一部分 光进入薄膜内部 并向下表面反射。
光学薄膜的制 备
光学薄膜的应 用领域拓展
光程差与薄膜干涉的关系
第四章
光程差对薄膜干涉的影响
添加标题
光程差与薄膜干涉的关系：光在薄膜上反射和折射时，由于入射角不同，光在薄膜上的反射和折 射路径长度也会不同，从而产生光程差。
添加标题
光程差对薄膜干涉的影响：光程差的大小直接影响薄膜干涉的强度和分布。当光程差较小时，干 涉条纹较为稀疏；当光程差较大时，干涉条纹较为密集。
实验步骤：激光束 通过分束器分成两 束，分别经过薄膜 样品的前后表面反 射，再回到屏幕产 生干涉现象
实验结果：观察干 涉条纹，测量光程 差，计算薄膜厚度
实验结果及分析
实验数据记录：详细记录实验过程中的各项数据，包括光程差、干涉条纹等 数据处理与分析：对实验数据进行处理和分析，得出光程差与薄膜干涉之间的关系 实验结论：根据实验结果得出光程差与薄膜干涉的结论，验证理论预测 实验误差分析：对实验过程中可能出现的误差进行分析，提高实验精度
光学传感器的应用前景
光学传感器在光 学领域的应用前 景
光学传感器在医 疗领域的应用前 景
光学传感器在环 保领域的应用前 景
光学传感器在军 事领域的应用前 景
感谢您的观看
汇报人：
薄膜干涉在光学中 的应用
光程差与薄膜干涉的相互作用
光程差与薄膜干涉的原理 光程差与薄膜干涉的相互作用过程 光程差与薄膜干涉的相互影响 光程差与薄膜干涉的应用

薄膜干涉光程差公式高中

薄膜干涉光程差公式高中

薄膜干涉光程差公式高中摘要：一、薄膜干涉光程差公式简介- 薄膜干涉光程差公式定义- 公式中各参数含义及物理意义二、薄膜干涉光程差公式推导- 薄膜干涉光程差公式推导过程- 注意要点及难点解析三、薄膜干涉光程差公式应用- 薄膜干涉在实际应用中的案例- 薄膜干涉光程差公式在案例中的应用四、总结与展望- 对薄膜干涉光程差公式的总结- 对未来薄膜干涉光程差公式的展望正文：一、薄膜干涉光程差公式简介薄膜干涉光程差公式，是描述光线在薄膜上下表面反射后，形成的干涉现象中，两束相干光之间的光程差与薄膜厚度、折射率等参数之间的关系公式。

它对于理解薄膜干涉现象、预测干涉条纹的分布以及进行薄膜厚度等参数的测量具有重要意义。

二、薄膜干涉光程差公式推导薄膜干涉光程差公式的推导过程涉及到一些光学基础知识，如光的折射、反射以及相干光的干涉等。

具体的推导过程如下：首先，假设光线在薄膜上下表面分别发生折射角为i和r的反射，光线在薄膜内部的传播距离为d，薄膜厚度为e。

根据光的折射定律，可以得到：1 * sin(i) = n2 * sin(r)其中，n1和n2分别为空气和薄膜的折射率。

接下来，考虑光线在薄膜上下表面反射后的光程差。

根据薄膜干涉的原理，光线在薄膜上下表面的反射光程差为2e，而在薄膜内部的传播光程差为d。

因此，总的光程差为2ne + λ/2，其中λ为光的波长。

最后，根据相干光干涉的原理，两束相干光之间的光程差应等于整数倍的波长，即2ne + λ/2 = m * λ，其中m为整数。

将上述两式联立，可以解得：e = (m * λ - λ/2) / 2n这就是薄膜干涉光程差公式。

三、薄膜干涉光程差公式应用薄膜干涉光程差公式在实际应用中有着广泛的应用，如薄膜厚度测量、光学薄膜设计等。

以下是一个具体的案例：在薄膜厚度测量中，假设我们已知光的波长为λ，折射率为n，以及干涉条纹的级次m。

通过测量干涉条纹的间距，可以得到：Δy = λ/m结合薄膜干涉光程差公式，可以求得薄膜厚度：e = (m * λ - λ/2) / 2n从而实现薄膜厚度的精确测量。

薄膜干涉


薄膜干涉条件： 薄膜干涉条件： 干涉加强： 1. 干涉加强：
λ , ∆ = 2d n − n sin i + = kλ k =1 2,L 2
2 2 2 1 2
干涉减弱： 2. 干涉减弱：
λ λ ∆ = 2d n − n sin i + = (2k +1 ) 2 2
2 2 2 1 2
k = 0,1 2,L ,
薄膜干涉
薄膜干涉反射光光程差
λ ∆ = n2 (A + B ) −n1A + B C D 2
由折射定律得： 由折射定律得： 1
P Q
D
n1 n2
i
A
2
i
r
B
C
d
λ ∆ = 2d n −n sin i + 2
2 2 2 1 2
n1 n2 > n1
λ ∆ = 2d n −n sin i + 2
2 2 2 1 2
每一条纹（ 每一条纹（即级 次）对应劈尖内一定 的厚度， 的厚度，当此厚度位 置改变时， 置改变时，对应的条 纹随之移动。 纹随之移动。
波长为680nm的平行光照射到 的平行光照射到L=12cm长的两块玻 例 波长为 的平行光照射到 长的两块玻 璃片上， 两玻璃片的一边相互接触， 璃片上 ， 两玻璃片的一边相互接触 ， 另一边被厚度 Ｄ=0.048mm的纸片隔开 . 试问在这 的纸片隔开. 的纸片隔开 试问在这12cm长度内会呈 长度内会呈 现多少条暗条纹 ? 解
劈尖干涉的应用 干涉膨胀仪 测膜厚
∆ l
n1 n2
si
sio2 e
l0
λ d=N 2n1
检验光学元件表面平整度
∆e

薄膜干涉的光程差公式

薄膜干涉的光程差公式薄膜干涉是一种光学干涉现象，是指当光线在两个介质之间传播时，由于不同介质的折射率不同，光线在介质中的传播路径不同，导致光程差的变化，从而产生干涉现象。

光程差是指光线传播过程中两条光线路径所走过的路程之差。

在薄膜干涉中，光线由真空中入射到一个介质中，然后再出射到另一个介质中。

设入射光线角度为θ，入射介质的折射率为n1，薄膜的厚度为d，薄膜的折射率为n2、在薄膜中，光线的路径可以分为两部分：一部分是入射光线在第一个介质中传播的路径，另一部分是入射光线在薄膜中传播的路径。

首先考虑入射光线在第一个介质中的传播路径。

入射光线在第一个介质中传播的路程为L1，由于第一个介质的折射率为n1，光线在此介质中的传播速度为c/n1，所以可以得到L1=c*t1，其中t1为光线在第一个介质中的传播时间。

根据物理学中的定义，光线在真空中的传播时间t为光线传播的路程L与光速c的比值，即t=L/c。

因此，L1=ct1=nc*t。

由此可见，入射光线在第一个介质中的传播路径与时间与真空中的传播路径和时间成正比。

接下来考虑入射光线在薄膜中的传播路径。

假设入射光线与薄膜表面的夹角为θ，入射光线在薄膜中传播的路程为L2、由于薄膜的厚度为d，光线传播的速度为c/n2，所以可以得到L2=d/cosθ*n2、其中cosθ为入射角的余弦值，n2为薄膜的折射率。

因此，入射光线在薄膜中的传播路径与薄膜的厚度和入射角的余弦值成正比。

最后考虑出射光线在第二个介质中的传播路径。

出射光线在第二个介质中的传播路径为L3、由于第二个介质的折射率为n1，光线在此介质中传播的速度为c/n1，所以可以得到L3=c*t3、根据上面的定义，可知L3=ct3=nc*t。

因此，出射光线在第二个介质中的传播路径与时间与真空中的传播路径和时间成正比。

根据光程差的定义，可以得到光程差为Δ=L1+L2+L3=(nc*t)+(d/cosθ*n2)+(nc*t)。

化简得到Δ=2nct+(d/cosθ*n2)。

第2节 光程差—薄膜干涉

4
2.光程差与相位差的关系（设两光同位相） 光程差与相位差的关系（设两光同位相） 光程差与相位差的关系 光程差每变化一个波长， 光程差每变化一个波长，相位差变化 2π 光程差为 δ ，相位差为∆ϕ ； 光程差与相位差的关系为： 光程差与相位差的关系为： δ = ∆ϕ λ 2π 2π 则相位差为： 则相位差为： ϕ = ∆ δ
13
①
i
n1 n2
②
d
n3
P
① i
A
D i
②
C
n1
r
B
n2
d
n3
δ ' = n2 ( AB + BC ) − n1 AD
AB = BC = d / cos r
①
D
P
AD = AC sin i = 2dtgr sin i
i i
A
i r r
B
②n
C
1
δ ' = n2 2 AB − n1 AD
n2
d
= 2n2d / cos r − 2n1dtgr sin i 2d = (n2 − n1 sin 2 i ) 由折射定律 n1 sin i = n2 sin r cos r 2n2d 2dn2 2 = cos2 r = 2n2d cos r δ '= (1 − sin r ) cos r cos r
n3
= 2n2d 1 − sin r = 2d n − n sin i
2
2 2
2 1
2
14
未考虑半波损失时
①
2 ′ = 2d n2 − n12 sin 2 i δ
i
n ②1 n2
d
考虑半波损失： 考虑半波损失：

薄膜干涉

§12-5 薄膜干涉 一、薄膜干涉的光程差公式
P i
n1 n2
2e n n sin i
2 2 2 1 2
a b
当 n1 > n2 > n3 ，
或 n1 < n2 < n3 时,
=0
γ i
2 2 2 1
e
n3
当 n1 < n2 > n3 或 n1> n2 < n3 时,
例如：当 n1 = n3 > n2 时，

10
五. 牛顿环
r2 R2
2e
2
R e
2
2 Re e 2 R e 可以略去e2 r2 e 2R r2 明环半径 k R 2
r
2k 1R
2
k 1,2 ,3
11
暗环半径
r
r2 R

2
2k 1
2
d N 2
若插入介质
2( n 1) L N
n N 2L 1
n,L N
14
二. 干涉现象的应用 三.相干长度 设波列长为L , 则两分光束产生干涉的最大光程差 m= L, 该长度即为单a1 a1a 1 S1 a a2 2 a2 S a2a2 b2 S2 a2

n2 1.38
e
2 2n2
由k=1得
emin

4n2
n3 1.50
0.1 μm
5
2e n n sin i
2 2 2 1 2
四. 劈尖干涉
平行光垂直入射
空气劈尖 ( n2 = 1 )
2e

2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

(r2 h nh) r1
当光程差为零时，对应零条纹的位置应满足：
r2 r1 (n 1)h 0 所以零级明条纹下移 原来 k 级明条纹位置满足： r2 r1 k
设有介质时零级明条纹移到原来第 k 级 k h 处，它必须同时满足：r2 r1 (n 1)h n 1
第二节
光程差 薄膜干涉
1
一、光程与光程差
1.光程
光源的频率不变，光在传播过程中频率保持不变。
在真空中光的波长为 ，光速为 C，进入折射率 为 n 的介质中后，波长n , 光速为 v ,则有： C C n 而 n v n v n 同一频率的光在不同介质中波长不相同。 处理方法：把光在介质中的波长折合成它在真空中的 波长作为测量距离的标尺，并进一步把光在介质中传 播的距离折合成光在真空中传播的距离。
l2 l1 d tg a d a (4)
由(3)和(4)得：劈尖b应向上移动的最小距离为
d 2 n 1 a 或 d 2 n 1 tg a
8
二、几个概念
1.薄透镜不引起附加光程差
透镜可以改变光线的传播方向，但是在光路 中放入薄透镜不会引起附加的光程差。
解:设 o 点最亮时,光线 2 在劈尖 b 中传播距离为 l1 ,则由双缝 S1 和 S2 分 别到达 o 点的光线的光 程差满足下式:

S1
S
1 2
b
o
S2
n 1 l1 k
7
(1)
设 o 点由此时第一次变为最暗时,光线 2 在劈尖 b 中传 播的距离为 l2 ,则由双缝 S1 和 S2 分别到达 o 点的两光 程差满足下式 1 c n 1 l2 k (2) 2 S1 1 (2) (1)得： o S 1 n 1 l2 l1 (3) 2 S2 2 b 由图可求出：
11
①
i
n1 n2
②
d
P
n3
i
D
① ②
C
i
A
n1
r
n2
B
n3
d
' n2 ( AB BC) n1 AD
AB BC d / cos r
①
P
AD AC sin i 2d tg r sin i
i i
A
D
' n2 2 AB n1 AD
i r
②n
C
1
2n 2 d / cos r 2n1d tg r sin i 2d (n2 n1 sin i sin r ) 由折射定律 n1 sin i n 2 sin r cos r 2n 2d 2dn2 2 2 cos r 2n 2 d cos r ' (1 sin r ) cos r cos r
i
n1
n1 n 2
当光从折射率大的光密介质， 正入射于折射率小的光疏介质 时，反射光没有半波损失。
10
r
n2
折射光都无半波损失。
三、薄膜干涉
单色光以入射角 i 从折 射率为 n1介质 进入折射率 为n2 的介质， 在薄膜的上下两表面产生的反射 光 ①光、② 光，满足相干光的 5 个 条件，能产生干涉，经透镜汇聚， 在焦平面上产生等倾干涉条纹。 从焦点 P 到 CD 波面，两 条光的光程差为 0，则在未 考虑半波损失时① 光、② 光的光程差为：
3
n


可以证明：光通过相等的光程，所需时间相同， 位相变化也相同。 如果光线穿过多种介质时，其光程为：
n1r1 n2r2 nn rn
r
1 n1
r
2 n2
ri ni
rn nn
n i ri
i 1
n
2.光程差 1 .光程差：两束光的光程之差。 设一束光经历光程1，另一束光经历光程2， 则这两束光的光程差为：
5
例2.在图示的双缝反射实验中，若用半圆筒形薄 玻璃片（折射率 n1=1.4 ）覆盖缝 S1，用同样厚 度的玻璃片（折射率 n2=1.7）覆盖缝 S2，将使屏 上原来未放玻璃时的中央明条纹所在处O变为第 五级明纹。设单色光波长 =480.0nm，求玻璃 片的厚度 d。 d 解：覆盖玻璃前 r2 r1 0 n S r
2 1
2.光程差与相位差的关系（设两光同位相） 2 则相位差为：
4

例1：已知：S2 缝上覆盖的介 质厚度为 h ，折射率为 n ， 设入射光的波为
S1Biblioteka r1r2h
S2
问：原来的零极条纹移至何处？若移至原来的第 k 级 明条纹处，其厚度 h 为多少？
解：从S1和S2发出的相干光所对应的光程差
6
例3.如图所示,用波长为 的单色光照射双缝干 涉实验装置,并将一折射率为 n、劈角为 a （a 很小）的透明劈尖 b 插入光线 2 中.设缝光源 S 和屏 c 上的 o 点都在双缝 S1 和 S2 在中垂线上.问 要使 o 点的光强由最亮变为最暗,劈尖 b 至少应 c 向上移动多大距离 d ( 只遮住S2 ) ?
2
设光在折射率为 n 的介质中传播的几何路程为 L， L vt 则 c C 有 L t即nL ct n v n 定义： 光程：光在介质中传播的波程与介质折射率的乘积。
nL
意义：光在t时刻内在真空中通过的路程nL就相当于 光在介质中在相同的时间内所通过的路程。 在一条波线上，波在介质中前进L，位相改变为： 2 2 2 L nL （同一波线上两点间的位相差）
1 1 1
覆盖玻璃后
r2 n2d d (r1 n1d d )
O
S2 n 2 r2 5 (n2 n1 )d 5 则有 d 5 / n 2 n 1 5 4 .8 10 7 / 1 .7 1 .4 8 10 6 m
F
F
波阵面
波阵面
通过光轴的光线波程最短，但在透镜中的光程长； 远离光轴的光线波程长，但在透镜中的光程短，总 的来讲，各条光线的光程都是相同的。
9
2.半波损失
半波损失：光从光疏介质进入光密介质，光反射后有 了量值为 的位相突变，即在反射过程中损失了半个 波长的现象。 产生条件：
n1 n 2
当光从折射率小的光疏介质，正入 射或掠入射于折射率大的光密介质 时，则反射光有半波损失。