当前位置：文档之家 › 由投影重建图像

由投影重建图像

  • 格式：pdf
  • 大小：636.13 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

图像处理第7章 图像投影重建

图像处理第7章 图像投影重建

设f(x,y)在以原点为圆心的单位圆Q 外为0，现考虑有一条由发射源到接 收器的直线在平面上与f(x,y)在Q内
相交，这条直线用两个参数来确定： 1，它与原点的距离s；2，它与Y轴 的夹角θ。
7.2.1 投影重建图像示意图
7.2.1 基本模型
沿直线（s, θ ）对 f（x,y)的积分
设Q为单位圆，积分上下限分别为t和-t
7.4 逆投影重建
7.4.1 逆投影重建原理
将从各个方向得到的投影逆向返回到该方向的各个位置，如果对多个 投影方向都进行这样的逆投影并叠加结果，就有可能建立平面上的一 个分布。
（a）分别给出水平投影和逆投影的示意图，发射源发出均匀射线，由 于所穿透物体各处密度不同，各接收器得到的响应不同。
（b）给出垂直投影和逆投影的示意图，与水平方向的效果类似
讨论接收器在一段弧上等角度间隔排列的情况，
用（s, θ）所指定的一条射线可看做是一组用（α，β）指定 的射线中的一条，其中α是该射线与中心射线的离散角，β 是源与原点连线和Y轴夹角，它确定了源的方向。
（7.2.5）
7.2.2 拉东变换
对f(x, y)沿一个固定角度投影结果的1-D傅里叶变换对 应f(x, y)的2-D傅里叶变换中沿相同角度的一个剖面/层， 如图7.2.3.
7.3 傅里叶反变换重建
基于变换的重建方法，它是首先在投影中得到应用的方法
1. 基本步骤和定义
(1) 建立数学模型，其中已知量和未知量都是连续实数的函数 (2) 利用反变换公式（可有多个等价的）解未知量 (3) 调节反变换公式以适应离散、有噪声应用的需求 重建算法： 设图象区被1个直角网格所覆盖，K为X方向上的点数，L为Y方向上的
(7.2.1)
7.2.2 拉东变换

图像重建

图像重建

恢复图像本来面目的处理措施。
④校正技术，即采用几何校正措施，去掉图像上的几何失真
。通过以上技术可以去除图像上的畸变及噪声信息，使图像 更加清晰，以便用目视准确判读和解释。
二 医学CT三维图像重建
二 分割标注 分割标注是保证三维重建准确性的关键技术,分割效果直接影 响三维重构的精确度。图像分割的目标是将图像分解成若干 有意义的子区域(或称对象) 。标注则为了能够识别出各区域 的解剖或生理意义。在医学图像领域,常常简单地将分割标 注的过程称为分割。 可简单的将医学图像分割分为两类:基于边界和基于区域。
例如,手术开窗，通过人机交互工具在重建出的人体器官立体视图上模拟
手术开刀,要求在计算机上迅速显示出模拟手术结果.
二 医学CT三维图像重建
重建流程图
二 医学CT三维图像重建
2 断层扫描原理
二 医学CT三维图像重建
（3）重建方法
在各种图像重建算法中，计算机断层扫描技术又称计算机
层析（CT）占有重要的地位。 计算机断层扫描技术的功能是将人体中某一薄层中的组 织分布情况，通过射线对该薄层的扫描、检测器对透射信 息的采集、计算机对数据的处理，并利用可视化技术在显 示器或其他介质上显示出来。 这项技术的重要基础是投影切片定理： 即对于任何一个三维(二维)物体，它的二维(一维)投影的 傅立叶变换恰好是该物体的傅立叶变换的主体部分。
基于边界的分割寻找感兴趣的封闭区域;
基于区域则是将体数据分为若干不重叠的区域,各区域内部
的体素相似性大于区域之间的体素相似性。
二 医学CT三维图像重建
（5）切片的重组、插值 CT 三维成像的主要方法是:通过多幅等间隔的相继断层图像 重建三维目标,实现人体组织器官的立体显示、操作和分析. CT 扫描仪得到的断层图像序列在空间三个正交的方向上分 辨率通常不同,例如,CT 切片中,层内像素距离通常在015 到 2mm之间,而层间距则位于1 到15mm 之间,断层内象素空间分 辨率远远高于各断层间的空间分辨率.如果直接用这种图像 进行分析处理和显示,由于三个方向空间分辨率不一致,使显 示结果呈阶梯状. 因此,要实现物体的三维显示和处理必须形成等分辨率的数 据,而内插是三维重建中必不可少的环节,内插效果直接影响 重建的质量.

CT

CT

I I 0e
μ 物 -μ 水 CT值 1000 μ水
• CT值：骨密质1000 空气-1000 水0 脑白质>脑灰质 凝固的血>血液
历史
• • • • • 伦琴：发现X射线 Rodon：图像重建 Bracewell：绘制太阳微波发射图像 Hounsfield：CT扫描机（头部） Ledley：全身CT扫描机
是就辐射出X射线。
• 球管外壳：作用：保证电子在真空管内能够自由加速，运动不受阻； 隔热与绝缘 类型：玻璃外壳；金属陶瓷外壳 • 阴极： 作用：发射电子，并使电子聚焦去轰击阳极。 组成：灯丝：钨丝 聚焦杯：把到达阳极的电子聚焦成一个窄束。 • 阳极：电子被加速至阳极，在阳极受阻，由于电子和靶材料之间的碰 撞，使得阳极产生热和电磁辐射。 分类：固定阳极：不能满足高负载的性能要求。 旋转阳极：提高热容量，提高功率，焦点小。绝缘油散 热和冷却。
各类CT扫描机
• • • • • • • • • • 第一代：平移+旋转扫描式——笔形扫描线束，时长伪影大 第二代：平移+旋转扫描式——扇形线束，射线利用率低 第三代：旋转- 旋转扫描式——较宽的扇形角 第四代：旋转- 静止扫描式——扇形线束角度大，对散射线及其敏感 第五代：电子束X射线管，对射线源要求比较高 螺旋CT（SSCT）：对整个容积进行快速连续扫描 多层面螺旋CT机（MSCT）：探测器呈弧面排列 双源CT 显微CT 工业CT
CT原理与技术
医工
什么是CT?
• CT是指由投影重建图像,由Hounsfield 发明，经历了五代。利用CT扫描成像 系统，完成数据采集、图像重建、图 像显示过程。对CT的评价可以从CT剂 量、系统参数及伪影来判定。
CT测什么
• • • 线性衰减系数（μ）：干涉散射、光电效应、康普顿效应的总和 在CT所用的较高能量的X射线中，康普顿效应起主导作用 朗伯-比尔定律：当一单色线束通过一密度均匀的小物体时，其能量与物质的 原子相互作用减弱，减弱程度与物质的厚度和组成成分或吸收系数有关， μ d • CT值：μ不具有很强的描述性，很大程度上取决于X射线光谱能量。相对于水 计算出来的μ为CT值。

图像重建原理

图像重建原理

F1{g (R)}
（3）卷积反投影法
卷积函数C(R)
卷积反投影函数改写成卷积的形式：
F11[F1{g (R) }] g (R) F11{ }
算法特点：将投影函数gθ(R)直接在空域中 进行修正，即将gθ(R)与一个事先设计好地 卷积函数C(R)进行卷积运算，然后将卷积后
利用积分式展开，可表示如下：


f (x, y)
0
d
[


g
(t)C(R
t)dt]
(x cos

y sin

R)dR


0 d g (t)C(x cos y sin t)dt


0 d g (R)C(x cos y sin R)dR

dd


d
0


G
( )e2jR

d
(x cos

y sin

R)dR


d
0
g '

(R)
(x
c os

y
s in

R)dR
g (R)
g' (R)
f (x, y)
1D FT
1D IFT
空间域 频域

F1{g (R)}
的结果作反投影。


f (x, y) 0 d {g (R) C(R)} (x cos y sin R)dR
卷积函数 C(R) F 1{ }
因 不可积，故对 重新定义如下：
lim e 0

CT图像重建技术

CT图像重建技术

CT图像重建技术CT图像重建技术000计算机层析成像(Computed Tomography，CT)是通过对物体进行不同角度的射线投影测量而获取物体横截面信息的成像技术，涉及到放射物理学、数学、计算机学、图形图像学和机械学等多个学科领域。

CT技术不但给诊断医学带来革命性的影响．还成功地应用于无损检测、产品反求和材料组织分析等工业领域。

CT技术的核心是由投影重建图像的理论，其实质是由扫描所得到的投影数据反求出成像平面上每个点的衰减系数值。

图像重建的算法有很多，本文根据CT扫描机的发展对不同时期CT所采用重建算法分别进行介绍。

第一代和第二代CT机获取一个单独投影的采样数据是从一组平行射线获取的，这种采样类型叫平行投影。

平行投影重建算法一般分为直接法与间接法两大类。

直接法是直接计算线性方程系数的方法，如矩阵法、迭代法等。

间接法是先计算投影的傅立叶变换，再导出吸收系数的方法，如反投影法、二维傅立叶重建法和滤波反投影法等[1]。

2.1 直接法2.1.1 矩阵法设一个物体的内部吸收系数矩阵为：(1)为了求得该矩阵中的元素值，我们可以先计算该矩阵在T个角度下的T组投影值 ,如设水平方向时 ,则：(2)同样其它角度下也有类似方程，把所有方程联立得到求解，即可求得所有u值。

通常情况下，由于联立方程组的数目往往不同于未知数个数，且可能有不少重复的方程，这样形成的不是方阵，所以一般不满秩，此时需要利用广义逆矩阵法进行求解。

2.1.2 迭代法实际应用中，由于图像尺寸较大，联立的方程个数较多，采用直接采用解析法难度较大，因此提出了迭代重建方法。

迭代法的主要思想是：从一个假设的初始图像出发，采用迭代的方法，将根据人为设定并经理论计算得到的投影值同实验测得的投影值比较，不断进行逼近，按照某种最优化准则寻找最优解[2]。

通常有两种迭代公式，一种是加法迭代公式[2]：（3）另一种是乘法迭代公式[2]：(4)两式中是相邻两次迭代的结果；是某一角度的实测投影值，是计算过程的计算投影值, 是投影的某一射线穿过点的点数，即计算投影值的射线所经过的像素的数目，是松弛因子。

数字图象处理 第5章 图像复原

数字图象处理 第5章 图像复原

（注①：若a(x),b(x) 为m维列向量，X为n维列
d daT dbT T 向量，那么： (a b) b a dX dX dX
注②：
dX T I dX
dX I T dX
）
ˆ 那么： f H 1 g
ˆ 若H已知，则可根据上式求出 f 。
2.2逆滤波（频域恢复方法）

ˆ 可以证明，对 f H 1 g 两边分别取傅立叶变换，
1.2 图像的退化模型
图像的退化和恢复模型如下图所示。
n( x, y )
f ( x, y )
h( x, y)
＋
g ( x,Байду номын сангаасy )
图像的退化由系统特性和噪声两部分引起。在这个 模型中，图像退化过程被模型化为一个作用在输入 图像f(x,y)上的系统H。它与一个加性噪声n(x,y)的 联合作用导致产生退化图像g(x,y)。
1.2 图像的退化模型
h( 2) h(1) h(0) h(1) h(0) h ( 2) h( 2) h(1) h(0) H h( 2) h(1) h(0) h( 2) h(1) h(0) h( 2) h(1) h(0)
其中未列出的元素均为零。
其中H为MN×MN维矩阵。
1.2 图像的退化模型
每个Hi是由扩展函数he(x,y)的第i行循环构成
he (i,0) h (i,1) Hi e he (i, N 1) he (i, N 1) he (i,0) he (i, N 2) he (i,1) he (i,2) he (i,0)
1.2 图像的退化模型
考虑到噪声，将延拓为M×N的噪声项加上，上式变为：

第六章 由投影重建图像 1.断层摄影图像的获取 2.重建图像的几种方法

第六章 由投影重建图像 1.断层摄影图像的获取 2.重建图像的几种方法
后所接收的信息叠加起来。
2) 反投影法
2) 反投影法

例如：把与A象素有关的z1 ,z3 ,z5叠加起来，可
知 A的值将和总和成正比。其他各个象素也一
样，事实上，叠加的结果都包含有 9 个象素的 总和，为保持射线密度的平均值不变，可以用 总象素数 9 去除总和，从而获得一个相应象素 的平均密度值，即重建图像的各个象素值分别
1）减少未知数数目
2）增加扫描路径
3）改变扫描路径
1) 解联立方程组方法

对于本问题，只有第三种 方程组为：
A B D z1 D E F z4 C D z2 B E z5 A B C z3 A C E z6
图(c)是改变扫描路径的情况，此时获得的新联立
些改变，但其基本原理还是相同的。下面我们
仅就 T-R 型扫描方式，讨论几种图像重建的方
法。
2. 重建图像的几种方法

常用的几种由投影重建图像的方法：
l解联立方程组方法 l反投影法 l利用傅立叶变换进行图像重建 l利用卷积进行图像重建
l图像重建的逐步逼近法
l最优化重建 l扇形投影数据的重建
1) 解联立方程组方法
复技术。如把投影看成是一种劣化过程，而重
建则是一种复原过程。具体来说，ห้องสมุดไป่ตู้投影时我
们丢失了沿射线方向的分辨能力(只剩1—D信
息)，而重建则利用多个投影恢复了2—D的分
辨力。
第六章 由投影重建图像

从投影重建图像的技术在许多科学领域，包括从分子
量级(借助电子显微镜)到宇宙量级(射电天文学)都得 到了应用。它极大地增强了人类观察物体内部结构的
收敛于对应象素值）而引起的结构模糊。

CT设备(2013)

CT设备(2013)

（一） X线管
Ｘ线管是产生Ｘ射线的器件，一般由阴极、 阳极和真空玻璃管（或金属管）组成。
1.Ｘ线管的发展
2.Ｘ线管损坏主要原因 3.Ｘ线管保护装置 4.Ｘ线管技术参数
1.Ｘ线管的发展
由于螺旋CT扫描需要长时间连续曝光，对 球管的散热率要求很高，采用大热容量球管， 能延长连续曝光时间，为解决这个问题，各厂 家都在不断地对球管进行改进。
GE公司采用了航天散热涂料增加阳极散 热率。 飞利浦公司金属轴承中空，冷却油进入阳 极靶核心而形成*透心凉*直接油冷技术，使球 管散热率进一步提高。 东芝公司采用阳极接地的方法加大球管散 热率。
Anode Grounded Technology
Aperture: Absorption of Recoil electrons • No Off-Focal X-ray • 30% less heat up
µ +µ +••••••+µn=1/△DlnIo/In 1 2
二、工作原理
（一）测量哪些数据 （二）如何测量一个物体 （三）如何计算一幅CT图像 （四）在CT图像中显示什么
（一）测量哪些数据 在CT中需要测量穿过人体之后的X 线强度，还要测定初始强度，计算从X线 源到探测器的每条射线上的衰减值，以 确定衰减分布函数µ （x ,y）。
（四）在CT图像中显示什么
CT测量并计算线性衰减µ （x,y）的空间分 布。不过，物理量µ 并不具备很强的描述性， 而且在很大程度上取决于X线光谱能量。对µ 的 定量描述是非常麻烦的；因为使用不同电压和 过滤器的CT所获得的图像，在它们之间进行直 接比较是毫无意义的。因此，定义了一个新概 念CT值，作为表达组织密度的统一单位。
为了纪念CT的发明者，将CT值的单位指定为 Hounsfield单位(HU)。对于一组织T，它的衰减系 数为µ ，则它的CT值可表示为 T CT值=（ µ –µ ）/ µ ×1000HU T 水 水 按此比例，水和每一种相当于水的组织，即 µ =µ ，它的CT值应为0HU。 因为 µ 空气几乎等 T 水 于0，所以空气的CT值为 -1000HU。水和空气的 CT值不受X线能量的影响，因此它们就成为CT值 标尺上的固定点。

滤波反投影法重建CT图像实验指导书一、实验目的1.了解傅立叶.docx

滤波反投影法重建CT图像实验指导书一、实验目的1.了解傅立叶.docx

滤波反投影法重建CT图像实验指导书一、实验目的1.了解傅立叶变换法、直接反投影法重建CT图像的原理;2.掌握滤波反投影法重建CT图像的原理和基木方法。

二、实验器材装有MATLAB程序的PC机，滤波反投影法图像重建演示软件，投影数据。

三、实验原理CT图像重建问题实际上就是如何从投影数据中解算出成像平面上各像索点的衰减系数。

图像重建的算法有多种，如反投影法、傅立叶变换法、迭代法、滤波反投彩法等。

在介绍算法前，有必要先介绍从投影重建图像的重要依据，即中心切片定理。

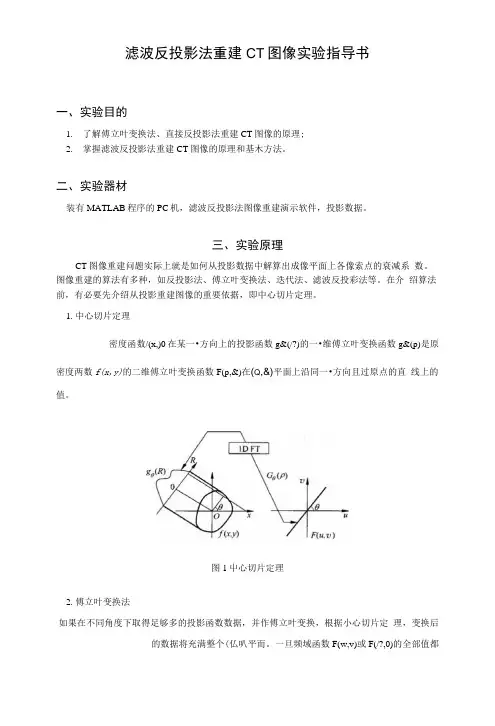
1.中心切片定理密度函数/(x,)0在某一•方向上的投影函数g&(/?)的一•维傅立叶变换函数g&(p)是原密度两数f(x,y)的二维傅立叶变换函数F(p,&)在(Q,&)平面上沿同一•方向且过原点的直线上的值。

图1屮心切片定理2.傅立叶变换法如果在不同角度下取得足够多的投影函数数据，并作傅立叶变换，根据小心切片定理，变换后的数据将充满整个(仏叭平而。

一旦频域函数F(w,v)或F(/?,0)的全部值都得到后，将真做傅立叶反变换，就能得到原始的密度函数.f(x,y)，即所要重建的图像。

上述图像重建算法称为傅立叶变换法，图2给出了傅立叶变换重建方法的流程图。

图屮指出，对于每次测得的投影数据先作一维傅立叶变换。

根据中心切片定理，可将此变换结果看成二维频率域屮同样角度下过原点的直线上的值。

在不同投影角卜•所得的一维变换函数可在频域中构成完整的二维傅立叶变换函数，将此二维变换函数做一次逆变换，就得到了所要求的空间域屮的密度函数。

为了在二维逆变换屮采用快速傅立叶变换算法，通常在逆变换前要将极坐标形式的频域函数变换成直角坐标形式的数据。

图2傅立叶变换重建图像的过程采用傅立叶变换法重建图像吋，投影函数的一维傅立叶变换在频域中为极处标形式, 把极坐标形式的数据通过插补运算转换为直角坐标形式的数据时，计算工作量较大。

此外, 在极坐标形式的频域数据屮，离原点较远的频率较高的部分数据比较稀疏，当这些位登上的数据转换到肯角坐标下时，需经插补，这将引入一定程度的谋差。

图像重建一般方法

图像重建一般方法
单束平移-旋转方式； 窄扇形束扫描平移-旋转方式； 旋转-旋转方式；


静止-旋转方式；
共同点是都需要X射线管和检测器之间进行 同步扫描机械运动。
38
计算机断层扫描技术
第一代CT (Computed Tomography)
单个探测器 平移－旋转并行光光束
39
第一代CT
1. 单束平移-旋转（T/R）方式
43
第二代CT
多个探测器 平移－旋转小扇形光束
(From G. Wang)
44
第三代CT
多个探测器 旋转－旋转大扇形光束
45
第三代CT
旋转-旋转（R/R）方式
这种扫描称为第三代 CT扫描，扫描装置由一个 X射线管和由 250～ 700个检测器（或用检测器阵列）排列成一个可在扫描 架内滑动的紧密圆弧形。 X 射线管发出张角为 30°～ 45°， 能覆盖整个受检体的宽扇形射线束。 由于这种宽扇束扫描一次 即能覆盖整个受检体，故 摄影区域 只需X射线管和检测器作 同步旋转运动。
11
X射线成像原理
当高速带电粒子撞击物质受阻而突然减速时，能够产生 X 射线。医学影像诊断所用的 X 线产生设备是 X 线管（ X-ray tube，球管）。 1．X射线的产生 X射线的产生需要的基本条件是： （1）有高速运动的电子流； （ 2 ）有阻碍带电粒子流运动的障碍物（靶），用来阻止 电子的运动，可以将电子的动能转变为 X 射线光子的能量 。
27
投影重建概述

概念：投影重建一般指利用物体的多个 （轴向）投影图像重建目标图像的过程。 它是一类特殊的图像处理方法，它输入的 是（一序列）投影图，而输出的是重建图。
通过投影重建就可以直接看到原来被投影 物体某种特性的空间分布，比直接观察投 影图要直观的多。

20081109070715工业CT简介(固鸿)

20081109070715工业CT简介(固鸿)

X射线工业CT简介一、工业CT的发展历程CT产生于20世纪70年代，但其物理根源可追溯到19世纪末。

1895年伦琴发现了一种能够穿过物体的不明射线，命名为X射线，并因此在1901年成为诺贝尔物理奖的第一位获得者。

20世纪初，X射线透射成像开始应用于临床医学诊断。

CT的算法起源要追溯到奥地利数学家J. Radon于1917年提出的观点：任何物体均可用无限多个投影来表示；反之，如果知道无限多个投影，便可重建该物体对象。

他成功地解决了由投影重建图像的数学问题，为CT技术的形成和发展奠定了理论基础，但在当时由于缺少有效的计算工具，一直被束之高阁，没有得到具体应用。

最初把断层成像术应用于医学领域的是Oldendor，他在1961年研制了用Y射线进行透射型成像的初级装置。

1963年美国物理学家Cormack首先提出用断层的多方向投影重建断层图像的代数计算方法。

第一台临床用的计算机断层成像扫描装置于1967年至1970年间由英国HMI公司的工程师Hounsfield研制成功。

Hounsfield和Cormack两人也因对CT 技术的卓越贡献而同获1979年诺贝尔医学奖。

CT技术首先应用于医学领域，对人体的病灶作断层扫描，然后以图像方式分析和确定病状，被称为医用CT (Medical CT即MCT)。

至今，医用CT已经家喻户晓，成为临床医学诊断不可或缺、最为有效的手段。

工业CT(Industrial CT，ICT)技术是在七十年代才逐渐开始研究的。

七十年代初期，曾直接利用医学CT的扫描设备进行工业检测，但始终不能满足实际检测的需要，于是进行了大量工业CT的研制工作，美、德、日、俄等国家在相关领域有不少成果。

美国在70年代末首先开始相关研究，1983年世界首台工业CT安装；1988年美国ARACOR公司研制出2MeV ICT1500，1990年升级为9MeV，1995年又生产了15MeV的ICT2500，并试验60MeV 工业CT；1994年日本研制成功12MeV工业CT；BIR、YXLON、HYTEC、OMEGA等公司也是工业CT领域的佼佼者。

CT图像重建(X线成像系统)

CT图像重建(X线成像系统)

ED=D×Wr

当辐射有多个种类和能量时，在一个组织或器官的 当量剂量就是各个辐射所致的当量剂量的和。
CT剂量

ED给出了不同辐射条件下人体发生生物效应的定量描述，但 人体不同组织或器官对辐射的敏感性和给人体造成的危害是 不同的。 因此又提出组织权重因子Wt（tissue weighting factor） 对上述的ED进行进一步修正。由Wr 和Wt两个因子修正后的 吸收剂量称为有效剂量（effective dose，ED）

伦琴表达照射量只用于能量低于3MeV的X线或 射线辐射，不 适合粒子辐射或能量高于3MeV的光子。 只适用于描述射线对空气的照射，并不能准确表达患者对辐射 的吸收。
பைடு நூலகம்

CT剂量


吸收剂量
描述组织吸收的射线能量 国际单位为：戈瑞（Gy） 1Gy=1J/kg 定义：1kg物质（人体组织）吸收1焦耳能量时的辐射量 吸收剂量D：质量为m（kg）的物质在辐射中吸收的能量 为E（J）时，其吸收剂量 D=E/m （Gy）


CT图像重建

直接反投影法的局限：
容易产生星形伪影
产生原因：反投影法把取 自有限物体空间的投影均 匀地回抹（反投影）到了 射线所及的无限空间的各 个像素上，包括原来像素 值为0的点。
CT图像重建
中心切片定理
CT图像重建

中心切片定理：某断层（或它对应的图像）f（x，y）在视角为 时 得到的平行投影（函数）的一维傅里叶变换，等于f（x，y）二维傅 里叶变换F（w1，w2 ）过原点的一个垂直切片，且切片与轴w1相交成


CT剂量
CT剂量
CT剂量
CT剂量
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4-5 由投影重建图像
一、 实验目的
了解反投影重建算法的方法.
二、 实验内容
1.利用radon 和iradon 函数实现平行束投影和反投影重建算法
2. 利用fanbeam 和ifanbeam 函数实现扇形束投影和反投影重建算法
三、 实验步骤
1.用MATLAB图像处理工具箱的phantom 生成Shep‐Logan 头模型；
P=phantom(256);
imshow(P);
2.用MATLAB中的radon 函数获得Shepp‐Logan 模型的投影数据：
theta1=0:10:170;
[R1,xp]=radon(P,theta1); %计算Shep‐Logen头模型18 个角度
theta2=0:5:175; [R2,xp]=r adon(P,theta2); %36 个角度
theta3=0:2:178;[R3,xp]=radon(P,theta3); % 90 个角度的投应
%显示投影数据：
%18 个角度
figure,imagesc(theta1,xp,R1);xlabel('\theta');ylabel('x\prime');
% 36 个角度
figure,imagesc(theta2,xp,R2);xlabel('\theta');ylabel('x\prime'); % 90 个角度
figure,imagesc(theta3,xp,R3);xlabel('\theta');ylabel('x\prime');
3．用MATLAB 中的iradon 函数对获得的投影数据进行滤波反投影重建，获得Shepp‐Logan 模型的重建图像：
I1=iradon(R1,10);I2=iradon(R2,5);I3=iradon(R3,2);
%显示重建图像：
figure,imshow(I1);
figure,imshow(I2);
figure,imshow(I3);
四、 实验总结
本次实验内容较少，通过本次实验我了解了反投影重建算法的方法.了解了利用radon 和iradon 函数实现平行束投影和反投影重建算法。

了解了利用fanbeam 和ifanbeam 函数实现扇形束投影和反投影重建算法。

对Shepp‐Logan 模型的投影不同角度的图行有了直观的了解。