文档CT图像滤波反投影重建算法的研究
- 格式:doc
- 大小:22.50 KB
- 文档页数:3


反投影重建算法
反投影重建算法(FBP)是一种计算机断层扫描成像(CT)重建图像
的方法。
该算法基于通过旋转体与X射线束的物理原理,将多个方向
的X射线透射数据进行积分,并使用反投影算法将数据重构成一张图像。
FBP算法分为两个基本部分:投影操作和反投影操作。
投影操作是一
种从图像中提取片段的技术,而反投影操作则是将这些片段重构成图像。
FBP重建算法的本质是一种频域过滤操作,其通过滤波技术提取
图像中的高频信息,并使用反投影技术将其还原为一张二维图像。
反投影重建算法的主要优点是其速度和适应性。
这种算法能够轻松地
生成高质量的图像,并且对于许多不同的应用程序都可以使用不同的
滤波模式。
目前,FBP算法被广泛应用于医学成像、工业检测和材料
科学等领域。
需要注意的是,FBP算法并不是完美的。
由于其基于体积的积分,因
此它可能受到一个“锐角偏差”问题的影响。
锐角偏差问题是指,当
图像中存在锐利的边缘或角落时,算法可能会出现伪影或失真的问题。
为了应对这个问题,一些改进算法被提出,例如金刚簇算法(来自中
国科技大学),基于块的迭代顺序最小化算法和模糊模式匹配算法等。
总之,反投影重建算法是一种实用的成像算法,对于许多不同的领域都具有广泛的适用性。
虽然这种算法具有其局限性,但是通过改进算法可以进一步提高它的可靠性和精度。
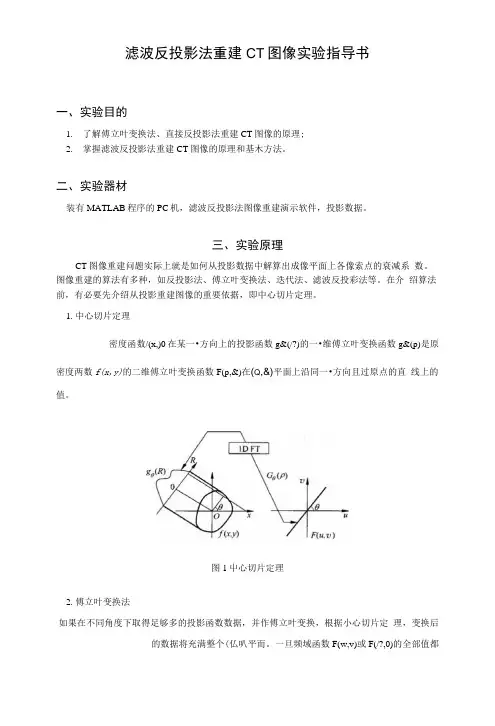
滤波反投影法重建CT图像实验指导书一、实验目的1.了解傅立叶变换法、直接反投影法重建CT图像的原理;2.掌握滤波反投影法重建CT图像的原理和基木方法。
二、实验器材装有MATLAB程序的PC机,滤波反投影法图像重建演示软件,投影数据。
三、实验原理CT图像重建问题实际上就是如何从投影数据中解算出成像平面上各像索点的衰减系数。
图像重建的算法有多种,如反投影法、傅立叶变换法、迭代法、滤波反投彩法等。
在介绍算法前,有必要先介绍从投影重建图像的重要依据,即中心切片定理。
1.中心切片定理密度函数/(x,)0在某一•方向上的投影函数g&(/?)的一•维傅立叶变换函数g&(p)是原密度两数f(x,y)的二维傅立叶变换函数F(p,&)在(Q,&)平面上沿同一•方向且过原点的直线上的值。
图1屮心切片定理2.傅立叶变换法如果在不同角度下取得足够多的投影函数数据,并作傅立叶变换,根据小心切片定理,变换后的数据将充满整个(仏叭平而。
一旦频域函数F(w,v)或F(/?,0)的全部值都得到后,将真做傅立叶反变换,就能得到原始的密度函数.f(x,y),即所要重建的图像。
上述图像重建算法称为傅立叶变换法,图2给出了傅立叶变换重建方法的流程图。
图屮指出,对于每次测得的投影数据先作一维傅立叶变换。
根据中心切片定理,可将此变换结果看成二维频率域屮同样角度下过原点的直线上的值。
在不同投影角卜•所得的一维变换函数可在频域中构成完整的二维傅立叶变换函数,将此二维变换函数做一次逆变换,就得到了所要求的空间域屮的密度函数。
为了在二维逆变换屮采用快速傅立叶变换算法,通常在逆变换前要将极坐标形式的频域函数变换成直角坐标形式的数据。
图2傅立叶变换重建图像的过程采用傅立叶变换法重建图像吋,投影函数的一维傅立叶变换在频域中为极处标形式, 把极坐标形式的数据通过插补运算转换为直角坐标形式的数据时,计算工作量较大。
此外, 在极坐标形式的频域数据屮,离原点较远的频率较高的部分数据比较稀疏,当这些位登上的数据转换到肯角坐标下时,需经插补,这将引入一定程度的谋差。

学术研讨109滤波反投影图像重建算法的◊西南石油大学理学院许珊珊谭兵CT图像重建在医学临床诊断等方面发挥了巨大的作用,滤波反投影算法是图像重建中应用最广泛的一种。
为了重建图像,我们使用了众所周知的傅立叶切片定理,利用逆Radon变换对研究对象进行滤波反投影图形重建。
实验结果表明,对于无嗓声图像,逆Radon变换能较好的完成重建任务,且投影角度数越多,重建图像就越清晰。
1引言各种成像系统依赖于通过计算机断层扫描(CT)过程来重 建图像。
在医学成像中,例如X射线CI拓描、磁共振成像(MRI)和各种类型的正电子发射断层扫描(PET)都记录着三 维物体的二维投影。
事实上,在没有任何关于被成像对象的假 设的情况下,有限数量的投影尚不能唯一且准确地定义原始对 象。
但是,通过组合来自多个投影的信息,可以产生对被成像 对象的精确描述。
于是在雷达成像中,人们可能再次希望合并 在不同角度获得的多个图像。
虽然这些场景彼此差异很大,但它们呈现出类似的数学问题,可以使用类似的技术来解决。
CT中的图像重建是一个数学过程,它根据许多不同角度下 采集的X射_影数据生成断层图像。
由于图像重建对图像质量 有着重大的影响,因此对辐射剂量也有影响。
对于给定的辐射 剂量,希望在不牺牲图像精度和空间分辨率的I f况下重建具有 最低噪声的图像。
优化图像重建过程可以等价于辐射剂量的减 少,因此可以在较低剂量下重建相同质量的图像。
2介绍在计算机断层扫描中,断层扫描重建问题是从一组投影获 得层析切片图像。
通过绘制一组平行射线穿过感兴趣的2D对象 形成投影,沿每条射线将物体对比度的积分分配给投影中的单 个像素。
2D对象的单个投影是一维的。
为了使对象的计算机断 层投影重建成为可能,必须获取多个投影,每个投影对应于射 线之间相对于对象的不同角度^多个角度的投影集合称为正弦 图,它是原始图像的线性变换。
存在两大类重建方法,分析重建和迭代重建。
本文主要关 注分析重建方法。

基于滤波反投影算法的CT系统参数标定及成像研究引言:计算机断层成像(CT)是一种利用X射线穿透人体及物体,通过对不同角度的投影数据进行处理和重建,获得精确的断层图像的技术。
滤波反投影算法是CT成像中最常用的重建算法之一,它能够高效地获得高质量的图像。
然而,在实际应用中,CT系统参数的准确标定对于获得精确的成像结果至关重要。
本文主要研究基于滤波反投影算法的CT系统参数标定及成像方法,旨在提高CT成像的精度和准确性。
1.CT系统参数标定方法1.1X射线束参数标定CT系统中的X射线束参数包括X射线束的发散角和聚焦点位置等。
通过在平板上放置一组密度均匀的标定物体,如骨骼或金属球,采集一组连续的X射线投影数据,并通过滤波反投影算法重建图像。
然后使用灰度剖面法计算图像中标定物体所占据的像素值范围,并在物体边缘处找到距离最远的像素点,从而得到X射线束发散角和聚焦点位置的标定结果。
1.2探测器参数标定CT系统中的探测器参数包括像素间距、灵敏度和线性度等。
针对像素间距的标定,可以在探测器平面上放置一组平行线标定物体,获得连续的X射线投影数据,并利用滤波反投影算法重建图像。
然后通过测量重建图像中平行线标定物体的实际像素间距,与探测器平面上的像素间距进行对比,即可以得到像素间距的标定结果。
对于灵敏度和线性度的标定,可以通过在探测器平面上放置一个均匀强度的平板,获得一组连续的X射线投影数据,并在滤波反投影算法重建图像中测量平板的平均像素值。
然后,与平板的实际强度进行对比,即可得到探测器的灵敏度和线性度的标定结果。
2.基于滤波反投影算法的CT系统成像方法2.1数据采集与预处理将对象置于CT系统内,通过旋转源和探测器获得一组连续的X射线投影数据。
然后,对数据进行预处理,包括背景校正、平面校正以及探测器响应校正等。
2.2滤波反投影重建利用滤波反投影算法对预处理后的X射线投影数据进行重建。
具体地,首先对投影数据进行滤波处理,消除投影数据中的噪声和伪影。
![文档CT图像滤波反投影重建算法的研究[宝典]](https://uimg.taocdn.com/65ffa4795901020207409c9d.webp)
文档CT图像滤波反投影重建算法的研究[宝典] 西北工业大学学位论文知识产权声明书本人完全了解学校有关保护知识产权的规定,即:研究生在校攻读学位期间论文工作的知识产权单位属于西北工业大学。
学校有权保留并向国家有关部门或机构送交论文的复印件和电子版。
本人允许论文被查阅和借阅。
学校可以将本学位论文的全部或部分内容编入有关数据库进行检索,可以采用影印、缩印或扫描等复制手段保存和汇编本学位论文。
同时本人保证,毕业后结合学位论文研究课题再撰写的文章一律注明作者单位为西北工业大学。
保密论文待解密后适用本声明。
学位论文作者签名::《~~~塑, 指导教师签名。
,况订年弓月多,日聊年岁月歹口日西北工业大学学位论文原创性声明秉承学校严谨的学风和优良的科学道德,本人郑重声明:所呈交的学位论文,是本人在导师的指导下进行研究工作所取得的成果。
尽我所知,除文中已经注明引用的内容和致谢的地方外,本论文不包含任何其他个人或集体己经公开发表或撰写过的研究成果,不包含本人或其他已申请学位或其他用途使用过的成果。
对本文的研究做出重要贡献的个人和集体,均已在文中以明确方式表明。
本人学位论文与资料若有不实,愿意承担一切相关的法律责任。
学位论文作者签名网年;月如日西北〕,业大学硕士学位论文第一章绪论第一章绪论本章首先概述了图像重建和,,技术的基本概念及图像重建方法的分类,然后介绍了,,的发展及国内外研究现状,最后阐明了本文的研究目的与意义、主要工作和内容安排。
,(,图像重建与,,技术概述由物体的二维截面或断面向该平面内的各个方向作投影,可获得一系列一维投影函数。
由这些一维投影函数来重建该二维截面则称为图像重建。
该技术是随着计算机技术的进步而发展起来并获得广泛应用的图像处理技术,其最典型的应用是医学上的计算机断层成像术(;,,,,,,, ,,,,鲫,,或;;胁,,,,,,,,,(,,,,肿,,,),简称为;,技术。
它用于获取人体头颅、心肺、腹部等内部器官的二维断层图像(故亦称断层摄影技术),对于,射线放射诊断是一个重大突破,具有深远的实际意义,因而受到普遍的重视。


基于滤波反投影算法的CT系统成像研究摘要:CT系统的安装会使得旋转中心发生偏离,从而影响成像质量,因此需要借助于已知结构的样品来标定CT系统的参数,并且利用标定的参数对未知结构的样品进行图像重建。
首先根据直接反投影算法和滤波反投影算法对收集到的数据中的接收信息分别进行图像重建,通过成像图像可知,滤波反投影算法更优;旋转中心可能发生偏移以及CT系统具有初始角度,依次进行旋转、平移、裁剪和残影去除操作,来校正投影图像,从而得到较高质量的图像。
关键词:CT成像原理(影像医学与核医学);滤波反投影法;图像重建;吸收率引言CT(Computed Tomography)是用X线束从多个方向对人体检查部位具有一定厚度的层面进行扫描,由探测器而不用胶片接收透过该层面的X线,转变为可见光后,由光电转换器转变为电信号,再经模拟/数字转换器转为数字,输人计算机处理。
数字矩阵中的每个数字经数字/模拟转换器转为由黑到白不等灰度的小方块,称之为像素,并按原有矩阵顺序排列,即构成CT图像。
所以,CT图像是由一定数目像素组成的灰阶图像,是数字图像,是重建的断层图像。
首先根据直接反投影算法和滤波反投影算法对收集到的数据中的接收信息分别进行图像重建,将图像重建[4-6]的两种结果进行对比,得出效果较好的模型;然后,旋转中心可能发生偏移以及CT系统具有初始角度,通过旋转、平移、裁剪和残影去除等操作来校正投影图像,最后对图像进行标准化调整,从而提高了成像质量。
1 模型的准备与建立1.1 CT成像的数学基础Rand变换如图1所示,直线g是xOy平面内任意一条直线,t是原点到直线g的距离,φ为原点到直线g的垂线与x轴的夹角。
对于xOy平面内任意一条直线可以由(t,φ)唯一确定。
二维平面中函数f(x,y)沿着直线的积分等于其Rand变换。
中心切片定理中心切片定理是CT图像重建算法的基础,在非衍射源情况下,含义是图像在某个视角下平行投影的一维Fourier变换等同于该图像二维Fourier变换的一个中心切片。

CT滤波反投影图像重建算法的反投影计算量问题
孙丰荣;刘积仁
【期刊名称】《中国生物医学工程学报》
【年(卷),期】2004(023)006
【摘要】本研究在综述扇束滤波反投影图像重建算法的基础上,分析并比较其中的二维反投影运算在直角坐标系和极坐标系下的计算量,然后提出一种极坐标系下的二维反投影运算过程优化方法,使计算量由O(N3)降至O(N2).本研究分析表明,选择在直角坐标系或极坐标系下直接实现二维反投影运算,不会使得其计算量发生数量级上的变化.但是,采取某些算法优化措施,能够显著地减少二维反投影运算过程的计算量.
【总页数】4页(P593-596)
【作者】孙丰荣;刘积仁
【作者单位】山东大学信息科学与工程学院,济南,250100;东北大学信息科学与工程学院,沈阳,110003
【正文语种】中文
【中图分类】R44:TP399
【相关文献】
1.滤波反投影图像重建算法研究 [J], 张顺利;李卫斌;唐高峰
2.关于滤波反投影图像重建算法的研究 [J], 李静
3.基于Hamming窗的滤波反投影CT图像重建算法 [J], 于尚民
4.动态滤波反投影图像重建算法研究 [J], 何世钧;韩宇辉;李照宇;高岩;李晖
5.滤波反投影图像重建算法的研究 [J], 许珊珊;谭兵
因版权原因,仅展示原文概要,查看原文内容请购买。

滤波反投影重建对CT系统研究确定CT系统旋转中心的位置、探测器单元的间距及X射线的180个方向[1];利用MATLAB获得模板示意图,对其处理得探测器单元间隔;建立坐标系,让X 射线入射光线与椭圆和圆的交线长度为约束条件,运用最小二乘法求得目标函数,利用遗传算法在MATLAB实现得到X射线的180个方向;重复上述方法旋转中心满足的约束条件和目标函数,得出旋转中心坐标,确定未知介质在正方形托盘的位置、几何形状和吸收率并利用滤波反投影法中的函数实现重建图像求得该介质的吸收率情况和10个位置处的吸收率.标签:遗传算法;滤波反投影;CT系统;最小二乘法0 引言CT系统就是利用样品对射线能量的吸收特性对生物组织和工程材料的样品进行断层成像,可以获取样品内部的结构信息。
但是CT系统安装时容易出现误差,所以要进行参数标定,并据此对未知结构的样品进行成像。
在正方形托盘上放置两个均匀固体介质组成的标定模板,确定CT系统旋转中心在正方形托盘中的位置、探测器单元之间的距离及该CT系统使用的X射线的180個方向。
1.求探测器单元之间的距离在正方形托盘上放置两个均匀固体介质组成的标定模板的几何信息,可以利用MATLAB对其进行计算绘制出该模板示意图(见图1)通过对比已知模板示意图可知右侧介质直径为8毫米。
然后对每一点的吸收率进行整理,利用MATLAB中的函数,利用这个函数将矩阵A中的元素数值按大小转化为不同颜色,并在坐标轴对应位置处以这种换颜色染色[2],其中决定坐标范围,是两个二维向量,即的范围内染色,根据图像及处理后的数据发现有84个角度没有穿过椭圆部分,对这84个角度进行统计得到有71个角度有29个探测器单元数据,对统计数据求取平均值估计探测器单元间隔d代入数据可得探测器单元间隔。
2.CT系统使用的X射线的180个方向通过CT成像的基本原理:X射线在穿过物质时,其强度的衰减与物质的厚度及入射辐射强度成正比,比例系数记作k,称为衰减系数,也等同于吸收系数,它代表X射线穿过单位厚度的物质时强度减少的比例,则吸收率W为W=kl根据为每一点的吸收率,则可以知道某次旋转时第个探测器上某点的吸收率和第个探测器上该点的吸收率。

基于FBP算法实现CT图像重建及模板优化一、引言计算机断层扫描(CT)技术是一种医学成像技术,能够通过X射线在人体内部产生的密度差异来获取图像信息。
CT图像重建是CT技术中的重要环节,它可以将X射线的投影数据转换成人体内部结构的精确图像,为医生提供诊断和治疗的依据。
在CT图像重建中,滤波反投影(FBP)算法是一种常用的重建算法,它通过对投影数据进行滤波和反投影操作来实现图像的重建。
本文将介绍基于FBP算法实现CT图像重建及模板优化的方法及应用。
二、FBP算法原理及实现FBP算法是一种基于投影数据的CT图像重建算法,它的基本原理是利用投影数据经过滤波和反投影操作来还原原始图像。
具体来说,FBP算法首先对投影数据进行滤波操作,以修正数据中的衰减和散射效应;然后通过反投影操作将滤波后的数据转换成原始图像。
整个过程可以用数学公式表示为:\[f(x,y) = \int_{0}^{2\pi} g(xcos\theta +ysin\theta,\theta)d\theta\]\(f(x,y)\)表示原始图像,\(g(x,y,\theta)\)表示投影数据,\(\theta\)表示投影角度。
FBP算法通过对投影数据进行滤波和反投影操作来实现\(f(x,y)\)的还原。
FBP算法的实现可以分为三个步骤:投影数据滤波、反投影操作和图像重建。
在投影数据滤波过程中,可以采用不同类型的滤波器来对数据进行滤波操作,例如Ram-Lak滤波器、Shepp-Logan滤波器等。
在反投影过程中,可以采用不同的反投影算法来将滤波后的数据转换成原始图像。
通过图像重建操作来生成CT图像并进行模板优化。
三、模板优化方法及应用1. 模板优化方法在CT图像重建中,模板优化是一种常用的图像后处理技术,它可以通过优化图像的灰度、对比度和边缘信息来改善图像的质量。
在FBP算法中,模板优化可以通过对图像进行局部直方图均衡化、增强边缘信息等方式来实现。
地理与生物信息学院2012 / 2013 学年第二学期实验报告课程名称:医学图像处理和成像技术实验名称:CT反投影滤波重建算法设计班级学号: B10090405学生姓名: 陈洁指导教师: 戴修斌日期:2013 年 5 月一、实验题目:CT反投影滤波重建算法设计二、实验内容:1.显示图像;2.获得仿真投影数据;3.基于获得的仿真投影数据重建图像。
三、实验要求:1.Shepp-Logan头模型:画出Shepp-Logan头模型,简称S-L模型,头模型尺寸设定为128×128;2.仿真投影数据的获得:从头模型中获得投影数据,投影数据格式为180×185,即[0,179°]范围内角度每隔1°取样,每个角度下有185个探测器;3.卷积反投影重建算法的实现:基于获得的仿真投影数据重建图像,使用R-L卷积函数,重建尺寸为128×128。
四、实验过程:实验1. Shepp-Logan头模型①算法实现流程:I. S-L头模型由10个位置、大小、方向、密度各异的椭圆组成,象征一个脑断层图像。
Shepp-Logan头模型中的椭圆参数:II. 使用循环语句给像素赋值:for i=1:10for x….for y…..判断点(x, y)是否在第i个椭圆内;如是,则将第i个椭圆折射指数赋给点(x, y);endendendIII. 显示仿真头模型:使用imshow(f,[])函数显示出图像。
②实验代码:clear all;p=[0 0 0.92 0.69 pi/2 10 -0.0184 0.874 0.6624 pi/2 20.22 0 0.31 0.11 72/180*pi 0-0.22 0 0.41 0.16 108/180*pi 40 0.35 0.25 0.21 pi/2 50 0.1 0.046 0.046 0 60 -0.1 0.046 0.046 0 7-0.08 -0.605 0.046 0.023 0 80 -0.605 0.023 0.023 0 80.06 -0.605 0.046 0.023 pi/2 8];N=256;x=linspace(-1,1,N);y=linspace(-1,1,N);f=zeros(N,N);for i=1:Nfor j=1:Nfor k=1:10A=p(k,3);B=p(k,4);x0=p(k,1);y0=p(k,2);x1=(x(i)-x0)*cos(p(k,5))+(y(j)-y0)*sin(p(k,5));y1=-(x(i)-x0)*sin(p(k,5))+(y(j)-y0)*cos(p(k,5));if((x1*x1)/(A*A)+(y1*y1)/(B*B)<=1) %判断条件f(i,j)=p(k,6);endendendendf=rot90(f);imshow(f,[])③运行结果:实验2. 获得仿真投影数据:①算法实现流程:I. θ∈ [00, 10, ..., 1790], s ∈[-92, -91, ..., 91,92];II. 对于第i 个椭圆求出对应θ和s 的仿真投影数据:其中,(x 0, y 0)为中心坐标,A 为长轴,B 为短轴,a 为旋转角度,ρ为折射指数。
西北工业大学学位论文知识产权声明书本人完全了解学校有关保护知识产权的规定,即:研究生在校攻读学位期间论文工作的知识产权单位属于西北工业大学。
学校有权保留并向国家有关部门或机构送交论文的复印件和电子版。
本人允许论文被查阅和借阅。
学校可以将本学位论文的全部或部分内容编入有关数据库进行检索,可以采用影印、缩印或扫描等复制手段保存和汇编本学位论文。
同时本人保证,毕业后结合学位论文研究课题再撰写的文章一律注明作者单位为西北工业大学。
保密论文待解密后适用本声明。
学位论文作者签名::《!!!塑L指导教师签名。
>况订年弓月多D日聊年岁月歹口日西北工业大学学位论文原创性声明秉承学校严谨的学风和优良的科学道德,本人郑重声明:所呈交的学位论文,是本人在导师的指导下进行研究工作所取得的成果。
尽我所知,除文中已经注明引用的内容和致谢的地方外,本论文不包含任何其他个人或集体己经公开发表或撰写过的研究成果,不包含本人或其他已申请学位或其他用途使用过的成果。
对本文的研究做出重要贡献的个人和集体,均已在文中以明确方式表明。
本人学位论文与资料若有不实,愿意承担一切相关的法律责任。
学位论文作者签名网年;月如日西北〕=业大学硕士学位论文第一章绪论第一章绪论本章首先概述了图像重建和CT技术的基本概念及图像重建方法的分类,然后介绍了CT的发展及国内外研究现状,最后阐明了本文的研究目的与意义、主要工作和内容安排。
1.1图像重建与CT技术概述由物体的二维截面或断面向该平面内的各个方向作投影,可获得一系列一维投影函数。
由这些一维投影函数来重建该二维截面则称为图像重建。
该技术是随着计算机技术的进步而发展起来并获得广泛应用的图像处理技术,其最典型的应用是医学上的计算机断层成像术(computedT0mo鲫hy或cc胁puterized.Ibmo肿pby),简称为cT技术。
它用于获取人体头颅、心肺、腹部等内部器官的二维断层图像(故亦称断层摄影技术),对于x射线放射诊断是一个重大突破,具有深远的实际意义,因而受到普遍的重视。
基于滤波反投影算法的CT系统参数标定及成像研究摘要本文主要针对CT系统的参数标定以及成像进行研究,在大致介绍CT设备及其成像原理的基础上,对题目所给问题进行分析计算解答,并采用基于滤波反投影重建算法的逆Radon 变换等算法对数据进行处理分析,得出结果,经过误差分析后,与CT系统自身特点相结合,结果比较理想。
问题一:根据X射线与标定模板的特殊位置如图(4)和图(8),两位之间角度90o,分析特殊位置图形,然后用MATLAB软件可画出CT系统绕某固定的旋转中心逆时针旋转180次的图,找到与特殊位置图形描述相近的图形,发现两特殊位置旋转次数差为90次,由此确定X射线的180个方向,探测器单元之间的距离=椭圆的长轴长/长轴长投影在探测器上单元的数量,由于旋转中心的位置和椭圆中心的位置相对不变,所以根据x和y的偏移量来确CT系统旋转中心在正方形托盘的位置。
问题二:建立CT系统滤波反投影重建算法,用iradon函数对附件2接收信息数据逆变换,即可得到出未知介质的吸收率,未知介质的几何形状,位置等信息。
问题三:由题意可知,该题同问题二相似,只是要求求另一种未知介质的相关信息,所以此题所用数学方法和问题二相同。
问题四:题目所给标定模型存在一定的规律性,并且容易受外界环境的影响,因此计算得到的CT系统参数存在误差。
所以我们自行设计了新的模板来改进标定精度和稳定性。
关键词:特殊位置、滤波反投影重建算法、逆Radon变换一、问题重述CT可以在不破坏样品的情况下,利用样品对射线能量的吸收特性对生物组织和工程材料的样品进行断层成像,由此获取样品内部的结构信息。
一种典型的二维CT系统是平行入射的X射线垂直于探测器平面,每个探测器单元看成一个接收点,且等距排列。
X射线的发射器和探测器相对位置固定不变,整个发射-接收系统绕某固定的旋转中心逆时针旋转180次。
对每一个X射线方向,在具有512个等距单元的探测器上测量经位置固定不动的二维待检测介质吸收衰减后的射线能量,并经过增益等处理后得到180组接收信息。
基于FBP算法实现CT图像重建及模板优化随着医学影像技术的不断发展,计算机断层扫描(CT)已成为一种常见的医学影像检查技术。
CT技术可以通过X射线对人体进行层次的扫描,从而获取人体内部的立体结构图像,为医生提供了重要的诊断信息。
在CT成像过程中,CT图像的重建是一个重要环节,对图像质量和清晰度有着重要的影响。
随着计算机技术的不断进步,一种基于滤波反投影(FBP)算法的CT图像重建方法得到了广泛应用。
本文将介绍基于FBP算法实现CT图像重建的原理、流程,并探讨其在模板优化方面的应用。
一、FBP算法原理及流程滤波反投影算法是目前最为常用的CT图像重建算法之一,它主要基于以下原理:在CT成像过程中,X射线透过人体后,会被不同程度吸收,因此最终在探测器上得到的信号是被衰减和吸收后的X射线信号。
通过这些信号,我们可以得到很多关于人体内部结构的信息,但最终需要将这些信息转化为图像的形式。
FBP算法就是利用这些信号,通过一系列数学模型和计算方法,实现对CT图像的重建。
FBP算法的流程一般包括以下几个步骤:首先是数据采集,即通过X射线扫描获得对应的探测器信号数据;然后是数据预处理,对采集到的数据进行校准和去噪处理;接着是滤波处理,通过使用不同类型的滤波器对数据进行滤波,以提取出图像的各种频率成分;最后是反投影处理,通过对滤波后的数据进行反投影计算,将其转换为图像象素值。
通过这一系列的步骤,FBP算法可以实现对CT图像的高质量重建。
二、FBP算法在模板优化方面的应用在实际的CT图像重建中,如何选择合适的滤波器和参数是一个非常重要的问题。
不同的滤波器和参数会对重建图像的质量和清晰度产生很大的影响。
通过对FBP算法进行优化,可以得到更高质量的CT图像。
在模板优化方面,主要包括以下几个方面:1. 滤波器的选择:滤波器的选择是影响CT图像质量的关键因素之一。
常见的滤波器包括Ram-Lak滤波器、Shepp-Logan滤波器等,它们在不同的应用场景下有着不同的效果。
探讨滤波反投影法和迭代算法对肺部CT图像质量的影响【摘要】目的探讨滤波反投影法(FBP)和迭代算法(IR)对肺部CT图像质量的影响。
方法选取100例健康患者,要求图像质量优良,能完全符合诊断要求,采用Philips Brilliance 256层螺旋CT(iCT)对肺部图像分别行FBP和IR重建,使用FBP方法重建图像为A组,使用IR方法重建图像为B组。
使用配对样本t检验对2组图像CT值、噪声(SD)、信噪比(SNR)、对比信噪比(CNR)进行统计学分析,p<0.05为差异有统计学意义。
结果 A组与B组CT值差异(p≥0.05)没有统计学意义,SD、SNR、CNR差异(p<0.05)均有统计学意义。
结论使用迭代重建方法能有效的减少图像的噪声,改善图像质量。
【关键词】体层摄影术;X线计算机;滤波反投影;迭代算法1972年第一台CT机问世以来,CT技术给医学诊断带来革命性的影响。
计算机断层扫描成像(Computerized Tomography简称CT)是利用一定能量的射线穿过人体时,不同厚度和原子序数的物质对射线衰减不同这一特性成像的。
也就是说,当射线穿过人体时,可以测量投射出后的投影,通过对不同方向得到的多个投影进行图像重建,来获取人体截面的图像。
CT图像重建常用的算法主要有解析法和迭代算法,解析算法中以滤波反投影算法(FBP)最具代表性,PHILIPS 256层螺旋CT iDose4技术为第四代迭代重建(IR)技术,去除各种低光子伪影,从而最有效地抑制低剂量伪影,去除噪音。
作者主要研究iDose4重建算法与FBP重建算法比较,对肺部图像质量的影响。
1.资料与方法1.1 一般资料选取我院2013年5月--2014年5月100例行肺部CT检查的患者,要求肺部纹理清晰,边缘锐利,没有明显的呼吸运动伪影及金属伪影,能完全满足诊断要求。
其中男43例,女57例,年龄范围40–85岁,平均68.5岁。
对同一患者分别用FBP和iDose4方法重建,使用FBP方法重建图像为A组,使用iDose4方法重建图像为B组。
西北工业大学学位论文知识产权声明书本人完全了解学校有关保护知识产权的规定,即:研究生在校攻读学位期间论文工作的知识产权单位属于西北工业大学。
学校有权保留并向国家有关部门或机构送交论文的复印件和电子版。
本人允许论文被查阅和借阅。
学校可以将本学位论文的全部或部分内容编入有关数据库进行检索,可以采用影印、缩印或扫描等复制手段保存和汇编本学位论文。
同时本人保证,毕业后结合学位论文研究课题再撰写的文章一律注明作者单位为西北工业大学。
保密论文待解密后适用本声明。
学位论文作者签名::《!!!塑L指导教师签名。
>况订年弓月多D日聊年岁月歹口日西北工业大学学位论文原创性声明秉承学校严谨的学风和优良的科学道德,本人郑重声明:所呈交的学位论文,是本人在导师的指导下进行研究工作所取得的成果。
尽我所知,除文中已经注明引用的内容和致谢的地方外,本论文不包含任何其他个人或集体己经公开发表或撰写过的研究成果,不包含本人或其他已申请学位或其他用途使用过的成果。
对本文的研究做出重要贡献的个人和集体,均已在文中以明确方式表明。
本人学位论文与资料若有不实,愿意承担一切相关的法律责任。
学位论文作者签名网年;月如日西北〕=业大学硕士学位论文第一章绪论第一章绪论本章首先概述了图像重建和CT技术的基本概念及图像重建方法的分类,然后介绍了CT的发展及国内外研究现状,最后阐明了本文的研究目的与意义、主要工作和内容安排。
1.1图像重建与CT技术概述由物体的二维截面或断面向该平面内的各个方向作投影,可获得一系列一维投影函数。
由这些一维投影函数来重建该二维截面则称为图像重建。
该技术是随着计算机技术的进步而发展起来并获得广泛应用的图像处理技术,其最典型的应用是医学上的计算机断层成像术(computedT0mo鲫hy或cc胁puterized.Ibmo肿pby),简称为cT技术。
它用于获取人体头颅、心肺、腹部等内部器官的二维断层图像(故亦称断层摄影技术),对于x射线放射诊断是一个重大突破,具有深远的实际意义,因而受到普遍的重视。
1.1.1图像重建图像重建是图像处理中一个重要研究分支,是指根据对物体的探测获取的数据来重新建立图像,其重要意义在于获取被检测物体内部结构的图像而不对物体造成任何物理上的损伤。
由于具备无损检测技术的显著优点,它在各个不同的应用领域中都显示出独特的重要性。
例如:在医疗放射学、核医学、电子显微、无线电雷达天文学、光显微和全息成像学及理论视觉等领域都多有应用。
在上述的众多领域中,图像重建在医学方面的应用最为显著。
它大大丰富了对于人体内部器官进行无损检测的方法和手段,为疾病的早期正确诊断提供了科学的、准确的依据。
根据原始数据获取方法及重建原理的不同可分为如下几种:发射断层重建成像(Emj醛i∞computcdTomography,Ec砷,透射断层重建成像frfansmissioncc吼plItcdTomo掣aphy,1∞,反射断层重建成像(Reflecti∞Cc粕puted劢衄ography,RcI)及核磁共振重建成像(Ma印eticRes∞卸cclIIIaging,MRn。
西北工业大学硕士学位论文第一章绪论1.1.2CT技术在各种图像重建算法中,计算机断层成像术即CT技术占有重要的地位。
cT技术的功能是将人体中某一薄层中的组织分布情况,通过射线对该薄层的扫描、检测器对透射信息的采集、计算机对数据的处理,并利用可视化技术在显示器或其他介质上显示出来。
1.1.3图像重建的方法图像重建是CT技术中的一个重要问题。
它的实质是按照采集后的数据,求解图像矩阵中象素,然后重新构造图像的过程;而图像矩阵的求解由计算机完成。
图像重建问题的求解方法根据其特点可分为2大类。
第1类是变换重建方法f也叫解析法呐,其特点是先在连续域解析处理,最后离散化以利用计算机计算。
其中又可分成傅里叶反变换重建法和滤波(或卷积)反投影重建法。
第2类是级数展开重建法12j13l(也叫代数重建法、迭代算法、优化技术等),其特点是从开始就离散化进行分析,从而直接得到数值解。
另外还有将变换法和级数展开法相结合的综合方法,如:迭代变换法、迭代重建重投影、角谐函数重建法和正交多项式展开重建。
变换法的突出优点是实现简单,速度快,对足够精确的投影数据能获得很好的重建质量。
因此目前实用CT系统中,尤其是医用cT系统中广泛采用变换法,特别是滤波反投影类型的算法来进行图像重建。
变换法在技术上有两个主要的限制:(1)噪声特性不好。
因为变换法是基于解析求反公式的闭合形式,要求投影数据是精确的。
对于数据中的噪声,可以通过滤波步骤来适当解决。
如果我们能在投影数据输入给变换法之前,将影响投影数据不精确性的诸多物理因素进行足够的校正,则便可以认为投影数据是相当准确的,从而得到满意的重建。
(乃正因为变换法基于解析求反公式的闭合形式,所以变换法的简单与复杂强烈地依赖于数据采集扫描方式。
如果投影数据不是沿直线的简单线积分,那么可能就得不到解析求反公式的闭合形式,在这样的情况下,变换法就变得无效。
级数展开法能和特定的成像设备及数据采集物理过程的特性相结合,并能利用某些先验信息。
这类方法尤其适合于数据采集过程具有高度统计特性及某些不能获得完整数据集的场合。
并且,级数展开法不像变换法那样强烈依赖于投影数据的采集方式,适合于投影数据不是目标函数沿直线而是沿曲线的积分甚至沿带2西北工业大学硕十学位论文第一章绪论状区域的积分。
级数展开法最大缺点是实现起来复杂,速度慢,并且所需的存储空间大。
因此,目前在实用CT系统中多不采用.1.2CT的发展与研究现状图像重建技术的历史比较悠久。
它的理论起源于1917年奥地利数学家Rad∞所发表的论文14l,文中证明了二维或三维物体的密度分布能够通过其无限多个投影来确定,数学上称之为Rad∞变换。
但限于当时的技术条件而未能在工程上实现,他的论文一直未被世人重视。
由于科学技术的进步,特别是计算机科学的发展,图像重建问题重新引起了人们的兴趣,相继有不少学者进行了卓有成效的创造性研究。
1963年,美国科学家A.M.‟ack首先提出了用x射线投影重建断层图像的计算方法。
19r72年,英国肼I公司中央研究所工程师G.N.H叫蚶eld研制成功诊断头颅用的第一台电子计算机x射线断层摄影装置,并在那一年的英国放射学年会上公布了这一装置及其应用成果,至此,才算真正设计出一个装置用来实现人体断面成像。
在1974年5月蒙特利尔召开的第一次国际Cr会议上,这一新式的x射线显像技术被正式命名为Cc胁putedT(皿ography,简称cT。
CT的问世在放射学界引起了爆炸性的轰动,被认为是继伦琴发现x射线后,工程界对放射学诊断的又一划时代的贡献。
1979年的诺贝尔生理和医学奖破例地授予两位没有专门医学资历的科学家:H∞sfield和Cc悯lack。
从此,放射诊断学进入了cT时代。
cT装置自问世以来,在其后的十多年内获得了极大发展,已从第一代产品发展到了第五代产品。
除X—Cr(用x射线作为辐射源,叫作x射线CT,简称x—C田以外,其他形式的cT也相继问世,如单光子发射cT(sPEcD、正电子发射叫PET)、核磁共振cT(NMR一叨等均已付诸临床应用。
超声CT、微波cT的研究也取得了极大的进展。
应该指出,各类cT的功能是相互补充而不是相互替代的。
cT作为一种高性能的无损诊断技术显然已在医学成像领域确立了不可动摇的地位。
实际上,临床上使用的x—cT设备的性能近年来又有了明显的提高。
为了进一步提高扫描速度,一些快速扫描装置相继诞生。
螺旋式超高速CT甚至可以对慢运动组织进行商分辨率的检查,并能提供人体组织的三维图像。
CT作为一种技术,既有坚实的数学理论为依托,又有现代微电子技术与计算机技术相支持,它已在工业无损检测、地球物理的研究、农林业和环境保护方3西北工业大学硕+学位论文第一章绪论面得到了广泛的应用。
1.3研究目的与意义在图像重建的变换重建方法中,滤波反投影算法(】Filte犯dbackprojccti∞,FBP)是影像重建中应用最广泛的一种算法,在当代x射线CT系统中几乎都用这种方法构成系统。
滤波反投影算法又称卷积反投影算法,因为频域上的滤波相当于空域上的卷积运算。
滤波反投影法大量实用的原因是它的基本算法很容易用软件和硬件实现,而且在数据质量高的情况下可重建出准确清晰的图像。
Hanley变换(HardcyTr姐sfo珊,HD是由著名数学家R.v.L.Hanley于1942年提出的一种正交变换151,它类似于F0lIricr变换(Fouri盱Tr柚sfo加,Fn,但它定义在实数域内,比Fr简单。
离散w变换(DiscrctewTransfom,DwD【6J是我国学者王中德提出的实数域上定义的一种正交变换。
1983年底,R.N.&accwcll研究了Hanley变换的离散形式,称之为离散Harlley变换(DiscfcteTransfonn,DH叫”,它实际上是DwT的一种特殊形式。
1994年,ⅢEE会刊(№din黟ofHanleymEE)出了一期关于Hartley变换的专刊【8l,可见这种变换已在实际应用中得到了广泛重视。
在实序列数据处理中,HT不仅等效于Fr,其正反交换又具有相同的形式,而且HT仅需用到实运算,在存储量和复杂性上要比FT更经济,在实数域能够替代FT进行信号和图像的处理。
有学者基于重建图像象素和投影射线之间在不同的投影方位上所存在的几何关系,提出了平行射束常规反投影的多方位同时反投影伽ultioricntati∞simun柚eous咖putatioⅡofbackp删ccti∞,MSBP)方法19J。
本文将Hanley变换和MsBP方法应用到CT图像的滤波反投影重建方法中,在保持精度不变的前提下,可较大地减少所需的存储空间和计算量。
1.4主要工作和章节安排论文主要完成的工作有:(1)对图像重建及CT技术的研究和发展情况进行了总结和评述,阐明了进行图像重建的目的和意义。
(2)对CT图像的反投影重建算法进行了详细的介绍,集中讨论了滤波4西北工业大学硕士学位论文第一章绪论反投影重建算法的计算机实现的具体步骤。
(3)对与FouIier变换平行的一种正弦正交变换—Hanley变换进行了探讨,根据用Hanlcy变换导出的滤波反投影重建算法重建CT图像,由此重建算法较Fourier方法将有大约一半计算量和存储空间的节省。
将平行射束常规反投影的多方位同时反投影(MSBP)方法应用于cT图像的滤波反投影重建方法中,使象素定位操作中的计算量减少到传统反投影算法的1/8。
(4)对(刁、(3)中采用的算法分别用MaⅡ曲进行了编程仿真,证明了算法的可行性,并对(3)中的方法与传统反投影方法的计算量和存储空间进行了比较和分析。