【学习课件】第三节格林公式及其应用

2) 若D不满足以上条件, 则可通过加辅助线将其分割 为有限个上述形式的区域 , 如图 y
Q P D x y d xd y Q P Q P ( )dxdy ( )dxdy x y x y D D
1
G A
L3 D3
F
C
D1
D2

0
r
例4. 计算
其中L为一无重点且不过原点 该方法俗称 “ 挖洞法 。”
y L
D
的分段光滑正向闭曲线.
(1) 当( 0, 0) D 时, xd y yd x Q P ( )dxdy L x 2 y 2 x y D (2) 当 ( 0,0) D 时,
解: 记L所围闭区域为D，
P Q 证: 将格林公式分为: dxdy Pdx， dxdy Qdy D y L D x L
1) 若D 既是 X - 型区域 , 又是 Y - 型区域 d
x 1 ( y)
y
E D
C
x 2 ( y)
A
B
bx
c
2 ( y ) Q Q d 则 d xd y d y dx D x 1 ( y) x c
Q 0, P y , 则有 A ydx
L
例1. 设 L 是一条分段光滑的闭曲线, 证明 证: 令 P 2x y , Q x 2 , 则
L
2x y d x x 2 d y 0
利用格林公式 , 得
L
2x y d x x 2 d y 0d x d y 0
A
D
y
L
o
x
B
L B O O A x dy L x dy x dy x dy x dy L BO OA 在BO上， y = 0 , d y 0, B O x dy 0

解 用格林公式。 记右半圆域为 D。 A Q P ( )dxdy 原式 x y D D
OA
OA
L
D
3dxdy
D
3 2 1 . 3| D | 0 sinydy cos 2
2
5/23
OA : x 0
D
例2. 求 (2x y4 )dx (3x5y6 )dy , L:
L
(0 ,0 ) 、 (3 ,0 ) 、 (3 ,2 )为 顶 点 的 三 角 形 ， 的 顺 边 时针方向。 D。 解 用格林公式。 记 相 应 三 角 域 为
原式
D

Q P ( ) dxdy x y D
L
3) 在 D 上， Pdx Qdy 与路径无 ；
AB
4) 在 D 上， Pdx Qdy 是某个函数的全 ( x, y) （ Qdy 是一个原函 . 数 即 有原函数 (x ,y ) Pdx
0 0
8/23
说明: 积分与路径无关时, 曲线积分可记为
P d xQ d y P dxQ dy AB A
21/23
r
x
Q P d x d y P d x Q d y 格林公式 x y D L
用格林公式易证： xOy 面上有界闭区 D 的面
| D| xdy D ydx
D
1 xdy ydx . 2 D
x a cos 所围面积 : ( 0 2 π) 例如, 椭圆 L y b sin 1 A x d y y d x 2L 2 π 1 2 2 πab ( ab cos ab sin ) d 0 2

那末 Pdx Qdy Pdx Qdy
L1
L2
由于 Pdx Qdy Pdx Qdy
L2
L2
即 Pdx Qdy 0 .
L1

L
2
L1 L2 是 G内一条有向闭曲线 .
因此 , G内由曲线积分与路径无关
可推出,在 G 内沿闭曲线的积分为零 .
G
DC
x
于是我们得到与定积分中莱布尼兹公式类似的公式 ,
(x, y) Pdx Qdy U (x, y) ( x0 , y0 )
(x , y) ( x0 , y0 )
U (x, y) U (x0 , y0 )
,
其中 L 为一条无重点 ` 分段光滑
且不经过坐标原点的连续曲线 , L的方向为逆时针方向.
解 令 P y , Q x .当 x2 y2 0 时,有
x2 y2
x2 y2
? ? Q
x
y2 x2 x2 y2 2
, P y
y 2 x2 , Q P . x 2 y 2 2 x y
记 L 所围的区域为 D : (1) 当 (0, 0) D , 由格林公式
y
L D

L
xdy x2

ydx y2



D
Q x

P y
dxdy

0
D
dxdy

0
.
o
x
(2) 当 (0, 0) D ,取 r 适当小, 作小圆l
l : x2 y 2 r 2 , 记 L l 所围的区域为 D1 .
y

例4. 计算 圆周
其中L 为上半
从 O (0, 0) 到 A (4, 0).
解: 为了使用格林公式, 添加辅助线段 AO , 它与L 所围 区域为D , 则
原式
L AO
( x 3 y ) d x ( y x) d y
OA
2
2
( x 2 3 y ) d x ( y 2 x) d y
A
D
B
bx
c
2 ( y ) Q Q d 则 d xd y d y dx D x 1 ( y) x c
d d c c
o a
C
Q( 2 ( y ), y ) d y Q( 1 ( y ), y ) d y

CBE
Q( x, y )d y
EAC
l
o D1
L

x
L l

2 0
r 2 cos 2 r 2 sin 2 d 2 2 r
山东农业大学
高等数学
主讲人： 苏本堂
二、平面上曲线积分与路径无关的条件 曲线积分与路径无关
设G是一个开区域 P(x y)、Q(x y)在区域G内具有一 阶连续偏导数 如果对于G内任意指定的两个点A、B以及G内从点A 到点B的任意两条曲线L1、L2 等式
山东农业大学
高等数学
主讲人： 苏本堂
格林公式的应用
1. 简化二重积分
例1. 计算 解: 令 P 0, Q xe
y2
其中D 是以 O(0,0) , A(1,1) ,
B(0,1) 为顶点的三角形闭域 . ,则
y
B(0,1) A(1,1)
D
利用格林公式 , 有

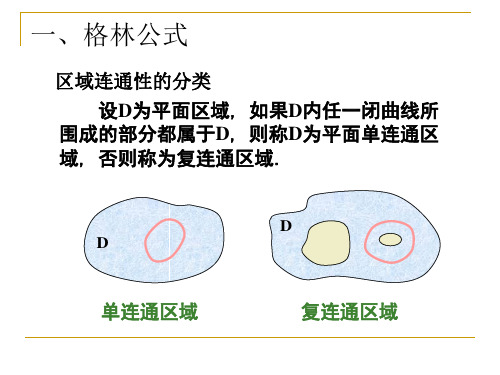
一、格林公式
区域连通性的分类 设D为平面区域, 如果D内任一闭曲线所
围成的部分都属于D, 则称D为平面单连通区 域, 否则称为复连通区域.
D D
单连通区域
复连通区域
L1
D
L2
L1
D
L2
L由L1与L2连成 L由L1与L2组成
边界曲线L的正向: 当观察者沿边界行走时,区 域D总在他的左边.
格林公式
定理1 设闭区域D 由分段光滑的曲线L 围
解 如果添加有向线段 OA，则 AnO + OA = L 是一条正向的封闭曲线.我们设由它围成的区域为
D.
y
因为 P(x, y) = exsin y –
n
my, Q(x, y) = excos y - m，
D
所以
A(a, 0)
O
x
Q Pexco y sexco y sm m , x y
则由格林公式得
L
( e x sy i m n ) d x y ( e x cy o m ) d s y OA
m πa2a0dx0m πa2.
8
0
8
2. 简化二重积分
y
例2 计算
ey2dxdy,其中D 是
B 1
D
D
以O(0,0), A(1,1),B(0,1)为顶点
的三角形闭区域.
o
解 令P 0, Q xey2 ,
d
d
cQ (2 (y )y ) ,d y cQ (1 (y )y ) ,dy
y
CQ B (x E ,y )d y CQ A (x E ,y )ddy E
x1(y)
D
Q (x ,y )d yQ (x ,y )dy

则
∂P −1 = ∂y x2 + y2
(
) (x
n
n
−
2n( x − y ) y
2
(x
x＋y
2
+ y2
)
n
∂Q 1 = ∂x x2 + y2
(
) (x
2 n
−
2n( x + y )x
2
+y
2 n +1
)
+y
2 n +1
)
为使
(x − y )dx + (x + y )dy
= πab
例 计算
3 xydx + x 2 dy ,其中L是矩形闭曲线 (如图). ∫L
由格林公式
∫ = ∫∫ (2 x − 3x)dxdy
L
3 xydx + x 2 dy
2
= ∫ dy ∫ (− x)dx = A
例 计算
(e x sin y − my )dx + (e x cos y − m)dy ∫
=
∂P ∂y
在D内恒成立；
(2) 对于D内任一闭曲线C，C Pdx + Qdy = 0 ∫ (3) 在D内曲线积分 证 (1)→(2) 因为D是单连域,所以闭曲线C所围成的区域G全部在D内, 应用格林公式,有
∂Q ∂P ∫C Pdx + Qdy = ∫∫ ( ∂x − ∂y ) dxdy = 0 G
L
其中L是A到O的上半圆(如图).
L为非闭曲线,直接计算较繁.
O 作辅助线OA,在闭曲线L+OA上用格林公式
mπa 2 = ∫∫ [e x cos y − (e x cos y − m)]dσ = ∫∫ mdσ = 8 D D

l D1
O D2
x
1
2π
d
1 2π
π
20
2
l :4x2 y2 2
法二
l
ydx xdy 4x2 y2
l
ydx
2
xdy
1
2
ydx xd y
l
格林公式
D2是由l 所围区域
4x2 y2 2
所以 I 0 π
π.
1
2
1
2
(1
D2
(2)
π
2
1)dxdy
2
π
25
10.3 格林公式及其应用
Pdx Qdy
L
(L1, L2, L3对D来说为正方向)
8
10.3 格林公式及其应用
(3) 对复连通区域证明:
对若复区连域通不区止域由D一, 格条林闭公曲式线
的右所曲端围线应成积 包.添分 括加,沿且直区边线域界段D的的A方全B向,部CE对边.区界 G D
域则DD来的说边都界是曲正线向由. AB, L2 , BA,
2π 0
格林公式
sin d(
2
(Q P )dxdy D1 x y 0
cos ) cos d(
2
2
0 sin
)
24
10.3 格林公式及其应用
l
ydx xdy 4x2 y2
2π
sin
d(
2
cos
)
2
cos
d(
sin
)
0
2
2 0
π
2
2
sin
2
2
2
2
cos2
d
y L: x2 y2 4

n (cos,cos).
v nds L
(P cos Q cos)ds
L
由格林公式
Pdy Qdx =========
(P Q )d .
L
D y x
（格林公式的另一种形式）
称函数
为平面向量场 v (P(x, y),Q(x, y))
的散度.物理意义：稳定流体通过某一闭曲线的流量，等
于其散度在该闭曲线所的区域上的二重积分之值.
(x y)dx (x y)dy
( L )
x2 y2
0dxdy 0.
D1
首页
上页
返回
下页
结束
铃
这里(L ) 表示多连通区域 D1的正向边界曲线 .这时L按 逆时针方向，而按顺时针方向.因而
(x y)dx (x y)dy
( L )
x2 y2
(x y)dx (x y)dy (x y)dx (x y)dy,
(x y)dx (x y)dy
L
x2 y2
1 r2
2 [r2 (cost sin t)(sin t) r2 (cost sin t)(cost)]dt
0
2
0 1dt 2.
例 4 设函数u(x,y)在有界闭区域D上有连续的二阶
偏导数，L 为D 的边界且逐段光滑.证明：
u
L
u n
ds
y
x
(x2 y)dx (x y2 sin3 y)dy, AO
oA
(x2 y)dx (x y2 sin3 y)dy
AO
0 x2dx 8 .
2
3
首页
上页
返回
下页
结束
铃
当曲线积分 (x2 y)dx (x y2 sin3 y)dy 与路径无 AB

另一种记法 :
x
DP
Green 公式
y Q
dxdy
ÑL Pdx
Qdy.
分析：
待证表达式
D
(
Q x
P )dxdy y
L Pdx
Qdy
等价于证明
D
Q x
dxdy
L
Qdy
D
P y
dxdy
LPdx
Y型区域
X 型区域
证明依赖于区域的形状
既 X又 Y型
单连通 一般区域
复连通
证明:
y
1. 若区域 D既是 X 型
1r 2 dxdy xdy xdy xdy xdy
4
D
L
OA
AB
BO
xdy dxdy 1 r2.
AB D
4
例 2 计算抛物线( x y)2 ax(a 0)与 x轴所
围成的面积.
解 ONA为直线 y 0.
曲线 AMO:
y ax x, x从a变到0.
M
L2
L3
L1
L Pdx Qdy
格林公式
D
Q x
P y
dxd
y
L
Pd
x
Qd
y
1.它建立了二重积分与曲线积分的一种等式关系; 2.它揭示了函数在区域内部与边界之间的内在联系.
格林公式
D
Q x
P y
dxd
y
L
Pd
x
Qd
y
推论: 正向闭曲线 L 所围区域 D 的面积
A 1 xdy y dx A xdy, A ydx.
r2
d
2π
Ñ 例4 计算 L
xdy 4x2

解: 为了使用格林公式, 添加辅助线段 区域为D , 则
它与L 所 围
原式
例5. 验证 数 , 并求出它.
证: 令
在右半平面 ( x > 0 ) 内存在原函
则 由定理 2 可知存在原函数
或
例6. 设质点在力场
由
移动到
作用下沿曲线 L : 求力场所作的功W
解:
令
则有
可见, 在不含原点的单连通区域内积分与路径无关.
第十一章
第三节 格林公式及其应用
一、格林公式
二、平面上曲线积分与路径无关的 等价条件
一. Green公式 闭曲线L的正向: 当沿此方向前进时,L所 围的区域 总在左边.
(Green公式)
格林公式 推论: 正向闭曲线 L 所围区域 D 的面积
例如, 椭圆
所围面积
例1 解
例2. 计算
其中D 是以 O(0,0) , A(1,1) ,
则
1) 计算曲线积分时, 可选择方便的积分路径;
2) 求曲线积分时, 可利用格林公式简化计算,
若积分路径不是闭曲线, 可添加辅助线;
3) 可用积分法求d u = P dx + Qdy在域 D 内的原函数:
取定点
及动点
则原函数为
或
例4. 计算
其中L 为上半
圆周
从 O (0, 0) 到 A (4, 0).
定理2. 设D 是单连通域 , 函数
在D 内
具有一阶连续偏导数, 则以下四个条件等价:
(1) 沿D 中任意光滑闭曲线 L , 有
(2) 对D 中任一分段光滑曲线 L, 曲线积分
ቤተ መጻሕፍቲ ባይዱ
与路径无关, 只与起止点有关.