格林公式及其应用

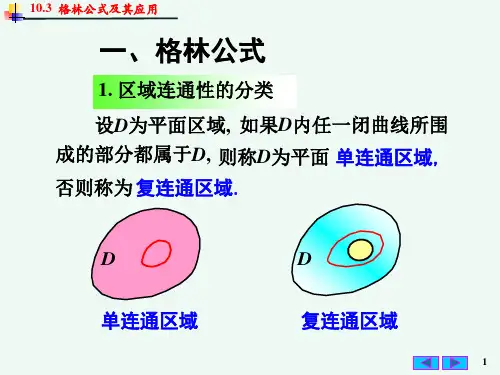
第三节格林公式及其应用一、格林公式1．单连通区域。

设D 为单连通区域，若D 内 任一闭曲线所围的部分都属于D 。

称D 为单连 通区域（不含洞），否则称为复连通区域（含洞）。

规定平面D 的边界曲线L 的方向，当观测者沿L 行走时，D 内在他近处的那一部分总在他的左边，如右图图10-3-1定理1（格林公式） 设闭区域D 由分段光滑的曲线L 围成，函数),(y x P 和),(y x Q 在D上具有一阶连续偏导数，则有dxdy yPx Q D⎰⎰∂∂-∂∂)(=L Pdx Qdy +⎰。

L 为D 的取正向的边界曲线。

证 对既为X -型又为Y -型区域2L ：)(2x y ϕ=∵yP∂∂连续， ⎰⎰∂∂D dxdy y P=dy y y x P dx x x b a ⎰⎰∂∂)()(21),(ϕϕ=dx x x P x x P ba})](,[)](,[{1121⎰-ϕϕ图10-3-21L ：)(1x y ϕ= 又⎰⎰⎰+=21L L LPdx Pdx Pdx=dx x x P ba ⎰)](,[11ϕ+dx x x P ba⎰)](,[21ϕ=dx x x P x x P ba})](,[)](,[{2111⎰-ϕϕ∴⎰⎰⎰=∂∂-L D Pdx dxdy y P对于Y -型区域，同理可证 ⎰⎰∂∂D dxdy y Q=⎰L Qdx ∴原式成立对于一般情况，可引进辅助线分成有限个符合上述条件区域，在4321,,,D D D D 上应用格林公式相加，由于沿辅助线积分是相互抵消，即可得证。

几何应用： 在格林公式中，取x Q y P =-=,，⎰⎰Ddxdy 2=⎰-Lydx xdy∴21=A ⎰-Lydx xdy说明：（1）格林公式对光滑曲线围成的闭区域均成立图10-3-3（2）记法⎰-Lydx xdy =⎰⎰∂∂-∂∂Ddxdy yx （3）在一定条件下用二重积分计算曲线积分，在另外条件下用曲线积分计算二重积分。

（4）几何应用。

例1 计算⎰++-Cdy y x dx x y )3()( L ：9)4()1(22=-+-y x解 原式=⎰⎰=-Ddxdy π18)13(，3=∂∂x Q ，1=∂∂yP例2 计算星形线⎩⎨⎧==ta y ta x 33sin cos 围成图形面积)20(π≤≤t 解 ⎰⎰⋅+⋅=-=π202223)sin cos 3sin cos sin 3cos (2121dt t t a t a t t a t a ydx xdy A L =832a π二、平面上曲线积分与路径无关的条件定理2 设区域G 是一个单连通区域，函数),(),,(y x Q y x P 在G 内具有一阶连续偏导数，则曲线积分⎰+LQdy Pdx 在G 内与路径无关（或沿G 内任意闭曲线的曲线积分为零）的充要条件是xQ y P ∂∂=∂∂在G 内恒成立。

例1 ⎰-++Ldy y x dx y x )()( 1L ：从)1,1(到)3,2(的折线 ；2L：从)1,1(到)3,2(的直线 解⎰+1L Qdy Pdx =25)1()2(2131=++-⎰⎰dx x dy y 3 2L ：)2(23-+=x y ,即 12-=x y⎰-++2)()(L dy y x dx y x =25)]1(2)12[(21=-+-+⎰dx x x x 图10-3-4定理 3 设),(y x P ，),(y x Q 在单连通区域D 内有连续的一阶偏导数，则以下四个条件相互等价（1）内任一闭曲线C ，⎰+CQdy Pdx =0。

（2）对内任一曲线L ，⎰+LQdy Pdx 与路径无关oyx(2,3)(1,1)L2L1（3）在D 内存在某一函数),(y x μ使Qdy Pdx y x d +=),(μ在D 内成立。

（4）xQy P ∂∂-∂∂，在D 内处处成立。

证明 （1）⇒（2） 在D 内任取两点B A ,，及连接B A ,的任意两条曲线⋂AEB ，⋂AGB ∴⋂⋂+=BGA AGB C 为D 内一闭曲线 由（1）知⎰+CQdy Pdx ，即⎰⋂+AGBQdy Pdx +⎰⋂+BEAQdy Pdx =0 ∴⎰⋂+AGBQdy Pdx =⎰⋂+BEA Qdy Pdx图10-3-5（2）⇒（3）若⎰+LQdy Pdx 在D 内与路径无关。

当起点固定在（0,yx ）点，终点为),(y x 后，则⎰+),(),(00y x y x Qdy Pdx 是y x ,的函数，记为),(y x u 。

下证 ),(y x u =⎰+),(),(00y x y x Qdy Pdx 的全微分为),(y x du =Qdy Pdx +。

∵),(y x P ，),(y x Q 连续，只需证),(y x P xu=∂∂，),(y x Q yu=∂∂， 由定义=∂∂x u 0()(,)lim x u x x u x y x ∆→+∆-∆=∆+),(y x x u ⎰∆++),(),(00y x x y x Qdy Pdx =),(y x u +⎰∆++),(),(y x x y x Qdy Pdx 图10-3-6=),(y x u +⎰∆+xx xPdx∴-∆+),(y x x u ),(y x u =⎰∆+xx xPdx =x P ∆，),(y x x P P ∆+=θ )10(≤≤θ即),(y x P x u =∂∂， 同理),(y x Q yu=∂∂。

（3）⇒（4）若),(y x du =Qdy Pdx +，可证y P ∂∂=x Q ∂∂，=P x P ∂∂，=Q yQ∂∂y x P y P ∂∂∂=∂∂，x y Q x Q ∂∂∂=∂∂， 由Q P ,具有连续的一阶偏导数=∂∂∂y x u 2xy u∂∂∂2 oyxE B AGx ∆),(000y x M oyxM(x,y)N(x+,y)故y P ∂∂=xQ ∂∂ （4）⇒（1）设C 为D 内任一闭曲线，D 为C 所围成的区域。

⎰+CQdy Pdx =dxdy yPx Q D⎰⎰∂∂-∂∂)(=0。

例2 曲线积分⎰-++=Lx ydy y xe dx x eI )2()(， L 为过)0,0(，)1,0(和)2,1(点的圆弧。

解 令x e P y+=，y xe Q y2-=，则y e xQ=∂∂，y e yP=∂∂ ∴I 与路径无关。

取积分路径为AB OA +。

=I ⎰+OAQdy Pdx +⎰+ABQdy Pdx图10-3-7=⎰⎰-++21)2()1(dy y e dx x y =272-e例3 计算⎰+-Cy x ydxxdy 22， （1）c 为以)0,0(为心的任何圆周。

（2）c 为以任何不含原点的闭曲线。

解 （1）令22y x y P +-=，22yx xQ +=， 22222)(y x x y y P +-=∂∂，22222)(y x x y x Q +-=∂∂， 图10-3-8∴在除去)0,0(处的所有点处有y P ∂∂=xQ∂∂，作以0为圆心，r 为半径作足够小的圆使小圆含在C 内，∴⎰⎰++rC CQdy Pdx =0，即=+⎰CQdy Pdx θθπd rr x r ⎰+202222sin cos =π2≠0 （2）∵y P ∂∂=xQ ∂∂ ∴=+⎰C Qdy Pdx 0三、二元函数的全微分求积oyxBAoyx),(00y x ),(y x oyx∵⎰+CQdy Pdx 与路径无关，则Qdy Pdx +为某一函数的全微分为),(y x u =⎰+),(),(00y x y x Qdy Pdx =⎰+x x Qdy Pdx 0+⎰+yy Qdy Pdx 0注：),(y x u 有无穷多个。

图10-3-9例4 验证：ydy x dx y x cos )sin 2(++是某一函数的全微分，并求出一个原函数。

解 令y x P sin 2+=，y x Q cos =y x Q cos =∂∂，y yPcos =∂∂ ∴ 原式在全平面上为某一函数的全微分，取)0,0(),(00=y x ，⎰+=),()0,0(),(y x Qdy Pdx y x u =⎰⎰+xyydy x xdx 0cos 2=y x x sin 2+例5 计算⎰-+-Cxxdy m e y dy my ey )3()(23， c 为从E 到F 再到G ，⋂FG 是半圆弧解 令my e y P x -=3， m e y Q x -=23m e y y P x -=∂∂23，x e y yQ 23=∂∂，图10-3-11添加直线GE ，则，原式+⎰+GEQdy pdx =⎰⎰-Dmdxdy=])22(211221[2π⋅+⋅⋅-m =)41(π+-m∴ 原式=m )41(π+-⎰-310dx =)41(π+-m例6 设)(x f 在),(+∞-∞上连续可导，求dy y x f y y xdx yy x f y L L ⎰⎰++)],([),(1222，其中为从点)32,3(A 到)2,1(B 的直线段。

解 令y y x f y P ),(12+=， ]1),([22-=y x f y yx Qo yxF(2,1)E(1,0)G (3,0)oyxBA CQ Pm x y∂∂-=∂∂图10-3-12222),(1)],(),(2[y y x f y y y x f xy y x yf y P --'+=∂∂=2321),(),(yy x f xy y x f y -+ =∂∂x Q ='+-)],([]1),([13222y x f y y x y x f y y 2321),(),(yy x f xy y x f y -+xQy P ∂∂=∂∂，故原积分与路径无关，添CB AC +构成闭路，∴ 原式+0=+⎰⎰AC BC ∴ 原式=⎰⎰+ACCB=dx x f dy y f y y )]32(941[23]1)([11322322++-⎰⎰dy y y f dx x f ⎰⎰-++=132322]1)([)]32(3223[ u x =3241)()(2323223223213-=+++⎰⎰y dy y f du u f x练习1.证明：若)(u f 为连续函数，而C 为无重点的按段光滑的闭曲线，则0)()(22=++⎰ydy xdx y x f c。

2.确定的n 值，使在不经过直线0=y 的区域上，dy y y x x dx y y x x I c nc n ⎰⎰+-+=222222)()(与路径无关，并求当C 为从点)1,1(到点)2,0(B 的路径时I 的值。

3．设),(y x f ，),(y x g 为L 上的连续函数，证明ds g f gdy fdx LL⎰⎰+≤+22小结：1. 格林公式及应用，积分与路径无关的四个等价命题，全微分求积。