格林公式及其应用
- 格式:doc
- 大小:189.50 KB
- 文档页数:4






格林公式的应用
1.什么是格林公式?
格林公式是指由英国数学家格林提出的用来计算某一多项式在
某一点的近似值的公式,它是一个多项式的近似值计算公式。
格林公式是基于抛物线(parabola)近似曲线在一定范围内拟合某多项式,其实际应用中是以三次多项式来近似计算出某多项式在某一点的近
似值。
2.格林公式的应用
(1)求解曲线的稳定点:格林公式可用来计算曲线的稳定点,即一阶导数为0时的值。
(2)优化函数:格林公式可用于优化函数,如果给定函数的一阶和二阶导,可利用格林公式求得函数的极值点。
(3)数值积分:格林公式也用于数值积分,能够准确而快速地求得曲线的积分值。
(4)对称函数:格林公式可用于求解对称函数的极值点,比如圆形的半径等。
(5)曲线拟合:格林公式也可以用于曲线拟合来确定某一多项式在某一点的值,从而降低计算的复杂度。
- 1 -。


格林公式及其应用格林公式格林公式是向量分析中的一个重要定理,也被称为格林-斯托克斯定理。
它是由爱尔兰数学家乔治·格林在19世纪提出的,用于计算一个曲线或曲面上的环流和散度之间的关系。
格林公式的应用非常广泛,可以用来求解流体力学、电磁学和热力学等领域的问题。
下面将介绍格林公式的表达形式,以及它在常见问题中的具体应用。
1.格林公式的表达形式格林公式有两种常见的表达形式,一种是针对平面区域的格林公式,另一种是针对空间曲线的格林公式。
下面将分别介绍这两种格林公式的表达形式。
1.1平面区域的格林公式若D是一个紧致的平面区域,边界为C(C是一个简单、逐段光滑的曲线),向量函数F(x,y)=(P(x,y),Q(x,y))在区域D中具有二阶连续偏导数,则有如下格林公式:∬D(∂Q/∂x-∂P/∂y)dxdy=∮C(Pdx+Qdy)其中,∂P/∂y和∂Q/∂x分别表示P和Q对y和x的偏导数,dxdy表示在D中的面积元素,Pdx+Qdy表示沿着边界C的曲线元素。
1.2空间曲线的格林公式若S是一个有向光滑曲面,它的边界为C(C是一个简单、光滑的曲线),向量函数F(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))在曲面S内具有连续偏导数,则有如下格林公式:∯S(∂R/∂y-Q)dydz+(∂P/∂z-R)dzdx+(∂Q/∂x-P)dxdy=∮C(Pdx+Qdy+Rdz)其中,∂P/∂z、∂Q/∂x和∂R/∂y分别表示P、Q和R对z、x和y的偏导数,dydz、dzdx和dxdy表示在S内的面积元素,Pdx+Qdy+Rdz表示沿着边界C的曲线元素。
2.格林公式的应用格林公式具有广泛的应用,在流体力学、电磁学、热力学等领域都能够找到它的身影。
下面将以几个例子来说明格林公式的具体应用。
2.1流体力学中的应用格林公式在流体力学中常常用于计算流体的环流和散度。
例如,可以利用格林公式来推导速度势函数和流函数之间的关系,进而求解流场中的速度分布。


格林公式及其应用
摘 要:
格林公式把二重积分化为曲线积分,从而简化了计算的过程。
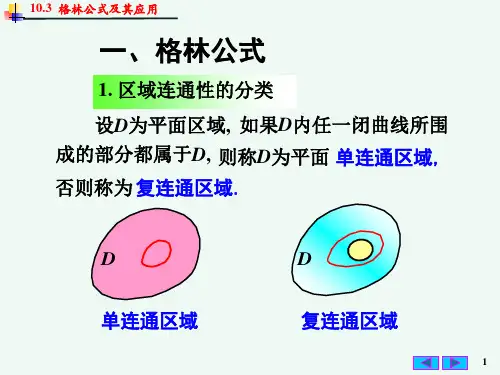
在介绍格林公式之前先引入平面区域连通性概念。
设D 为一平面区域,如果区域D 内任意区域所围成的部分都属于D ,则称D 为平面单连通区域,否则称为复连通区域。
关键词 闭区域D ;格林公式;积分与路径的关系;曲线积分;二重积分;
引言
格林公式是英国数学家格林发明,他通过这个公式来求关于面积、二重积分、第二类曲线积分与路径的关系等问题。
其定义是:设闭区域D 由分段光滑的曲线L 围成,函数P (x,y )及Q (x,y )在D 上具有一阶连续偏导函数,则有
⎰⎰⎰
+=∂∂-∂∂L D
Qdy Pdx dxdy y
P
x Q )(
,其中L 是D 的取正向边界曲线
格林公式转化的物理意义: 二重积分——第二类曲线积分
将一物体计算体积的值转化为计算绕该物体地面一周所做的功
定理1 设闭区域D 由分段光滑曲线L 围成,函数P (x ,y )及函数Q (x ,y )
在D 上具有一阶连续偏导数,则有
D D
Q P Pdx Qdy dxdy x y +∂⎛⎫
∂∂+=- ⎪∂∂⎝⎭⎰⎰⎰D y dxdy x P Q
∂∂∂=∂⎰⎰
其中L 是D 的取正向的边界曲线,此公式即为格林公式
证明:
(1)若区域D 既是-X 型又是-Y 型,即平行于坐标轴的直线和L 至多交于两
点.
}),()(),{(21b x a x y x y x D ≤≤≤≤=ϕϕ}),()(),{(21d y c y x y y x D ≤≤≤≤=ψψ
dx x Q dy dxdy x Q
y y d c D
⎰⎰⎰⎰∂∂=∂∂)()(21ψψ ⎰⎰-=d
c
d c
dy y y Q dy y y Q )),(()),((12ψψ
x
x x
⎰
⎰-=CAE
CBE
dy y x Q dy y x Q ),(),( ⎰
⎰
+=EAC
CBE
dy y x Q dy y x Q ),(),(
⎰=L
dy y x Q ),(
同理可证⎰⎰⎰
=∂∂-L D
dx y x P dxdy y
P
),(
两式相加得⎰⎰⎰+=∂∂-∂∂L D
Qdy Pdx dxdy y
P
x Q )(
(2)
若区域D 由按段光滑的闭曲线围成.
如图
将D 分成三个既是-X 型又是-Y 型的区
域1
D ,2
D ,3
D .
⎰⎰⎰⎰++∂∂-∂∂=∂∂-∂∂3
21)()(D D D D dxdy y P x Q dxdy y P x Q ⎰⎰⎰⎰⎰⎰∂
-∂∂+∂∂-∂∂+∂∂-∂∂3
21
)()()(
D D D dxdy y x Q dxdy
y P x Q dxdy y P x Q ⎰⎰⎰
+++++=
3
2
1
L L L Qdy Pdx Qdy Pdx Qdy Pdx
⎰+=L
Qdy Pdx
(3)
若区域不止由一条闭曲线所围
成.添加直线段AB,CE.则D 的边界曲线由AB,2
L ,BA,
AFC,CE,
3L , EC 及CGA 构成
由(2)知⎰⎰∂∂-∂∂D
dxdy y P
x Q )(
⎰
⎰⎰⎰⎰+
+++=CE
AFC BA L AB 2
{
⎰
⎰⎰+⋅+++CGA
EC L Qdy Pdx )(}3
),(32,1来说为正方向对D L L L
⎰⎰⎰+++=2
3
1
))((L L L Qdy Pdx ⎰+=L
Qdy Pdx
应用:
(1)用格林公式计算区域的面积
设区域D 的边界曲线为L , 则
例1 求椭圆x =a cos q , y =b sin q 所围成图形的面积A . 解设L 是由椭圆曲线, 则
(2)用格林公式计算二重积分
为顶点的三角形闭区域.
因此, 由格林公式有
(3)用格林公式求第二类曲线积分
⎰-=L ydx xdy A 2⎰
+=πθθθ2022)cos sin (21d ab ab
-L ydx xdy 1⎰+=πθθθ2022)cos sin (21d ab ab πθπab d ab ==⎰2021. πθπab d ab ==⎰20
21. )1(2111
02
2----===⎰⎰e dx xe dy xe x OA y . 1(2
111
2
2
----===⎰⎰e dx xe dy xe x OA
y . ),(32,1来说为正方向对D L L L ⎰-=L ydx xdy A 21.
例2 计算⎰⎰-D
y dxdy e
2
, 其中D 是以O (0, 0), A (1, 1), B (0, 1)
.
令P =0, 2
y xe
Q -=, 则
2y e y
P
x Q -=∂∂-∂∂. ⎰⎰⎰++-
-=
BO
AB OA y D
y dy xe dxdy e 22 ⎰⎰⎰
++--=BO AB OA y D y dy xe
dxdy e 22
1(2
111
02
2
----===⎰⎰e dx xe dy xe x
OA
y .
例3
不经过原点的连续闭曲线, L 的方向为逆时针方向. 解:记L 所围成的闭区域为D .
当(0, 0)∈D 时,在D 内取一圆周l : x 2+y 2=r 2(r >0). 记L 及l 所围成的复连通区域为D 1, 应用格林公式得
其中l 的方向取顺时针方向.
(4)平面上曲线积分与路径无关的条件
解:这里P =2xy , Q =x 2.
选择从O (0, 0)到A (1, 0)再到B (1, 1)的折线作为积分路线,
例5 计算⎰+L
dy x xydx 22, 其中L 为抛
物线y =x 2上从O (0, 0)到B (1, 1)的一段弧
.
0)(1
2
2=∂∂-∂∂=+-⎰⎰⎰+dxdy y P x Q y x ydx xdy D
l
L , ⎰⎰-+-=+-l L y x ydx xdy y x ydx xdy 2222⎰+=πθθ
θ2022222sin cos d r
r r =2π. -+-=
l y x ydx xdy 22⎰+=πθθθ2022222sin cos d r r r =2π. -+-=+-l y x
ydx xdy y ydx y 2222
⎰+=πθθθ20
2
2222sin cos d r
r r =2π. 因为
x
x
Q y P 2=∂∂=∂∂, 所以积分
⎰+L dy x xydx 22与路径无关. 则 ⎰⎰⎰+++=+AB
OA
L
dy x xydx dy x xydx dy x xydx 222222
111
2==⎰dy .。