3.2格林公式及其应用

格林公式的讨论及其应用格林公式是矢量分析中的重要定理之一，它描述了向量场在一个闭合曲面上面的流量与该向量场的散度在该闭合曲面所围成的空间体积之间的关系。

格林公式广泛应用于电磁学、流体力学、热力学等领域，下面将对格林公式进行详细讨论及应用。

格林公式可以用数学的方式描述为：对于一个可微的矢量场F，它的散度为div(F)，则该矢量场F通过一个闭合曲面S的流量为∬F⋅ds，该闭合曲面S所围成的体积为∭div(F)dV，格林公式表达了这两者之间的关系，即：∬F⋅ds = ∭div(F)dV其中，∬表示曲面积分，∭表示体积积分，F⋅ds表示矢量场F与ds 的内积，div(F)表示矢量场F的散度。

1.流体力学中的应用格林公式在流体力学中有着广泛的应用。

例如，可以通过格林公式计算流体在一个闭合曲面上的流量，这对于流体的体积流量和质量流量的计算有重要意义。

另外，格林公式还可以用来推导流体的连续性方程和Navier-Stokes方程等重要方程。

2.电磁学中的应用格林公式在电磁学中也有着重要的应用。

例如，可以利用格林公式计算电磁场在一个闭合曲面上的通量，这对于计算电场和磁场的电荷和磁荷的分布有着重要意义。

此外，通过格林公式还可以推导出麦克斯韦方程组中的一些重要方程，如高斯定律、安培环路定理等。

3.热力学中的应用格林公式在热力学中也有着重要的应用。

例如，可以通过格林公式计算热场在一个闭合曲面上的通量，这对于计算热量的传递和热功的计算有着重要意义。

此外，格林公式还可用于推导出热传导方程等重要方程。

除了上述应用之外，格林公式还广泛应用于流场分析、电磁场分析、电力系统分析等领域。

在实际应用中，可以利用格林公式对复杂的问题进行推导和计算，从而得到更加精确的结果。

总结起来，格林公式是矢量分析中的重要定理之一，描述了向量场在一个闭合曲面上面的流量与该向量场的散度在该闭合曲面所围成的空间体积之间的关系。

它在流体力学、电磁学、热力学等领域都有重要的应用。

格林公式及其应用格林公式格林公式是向量分析中的一个重要定理，也被称为格林-斯托克斯定理。

它是由爱尔兰数学家乔治·格林在19世纪提出的，用于计算一个曲线或曲面上的环流和散度之间的关系。

格林公式的应用非常广泛，可以用来求解流体力学、电磁学和热力学等领域的问题。

下面将介绍格林公式的表达形式，以及它在常见问题中的具体应用。

1.格林公式的表达形式格林公式有两种常见的表达形式，一种是针对平面区域的格林公式，另一种是针对空间曲线的格林公式。

下面将分别介绍这两种格林公式的表达形式。

1.1平面区域的格林公式若D是一个紧致的平面区域，边界为C（C是一个简单、逐段光滑的曲线），向量函数F(x,y)=(P(x,y),Q(x,y))在区域D中具有二阶连续偏导数，则有如下格林公式：∬D（∂Q/∂x-∂P/∂y）dxdy=∮C(Pdx+Qdy)其中，∂P/∂y和∂Q/∂x分别表示P和Q对y和x的偏导数，dxdy表示在D中的面积元素，Pdx+Qdy表示沿着边界C的曲线元素。

1.2空间曲线的格林公式若S是一个有向光滑曲面，它的边界为C（C是一个简单、光滑的曲线），向量函数F(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))在曲面S内具有连续偏导数，则有如下格林公式：∯S（∂R/∂y-Q）dydz+（∂P/∂z-R）dzdx+（∂Q/∂x-P）dxdy=∮C(Pdx+Qdy+Rdz)其中，∂P/∂z、∂Q/∂x和∂R/∂y分别表示P、Q和R对z、x和y的偏导数，dydz、dzdx和dxdy表示在S内的面积元素，Pdx+Qdy+Rdz表示沿着边界C的曲线元素。

2.格林公式的应用格林公式具有广泛的应用，在流体力学、电磁学、热力学等领域都能够找到它的身影。

下面将以几个例子来说明格林公式的具体应用。

2.1流体力学中的应用格林公式在流体力学中常常用于计算流体的环流和散度。

例如，可以利用格林公式来推导速度势函数和流函数之间的关系，进而求解流场中的速度分布。

格林公式及其应用格林公式是微积分中的一个重要工具，用于计算其中一区域内的面积和体积。

它是由德国数学家格林（Carl Friedrich Gauss）在19世纪初提出的，被广泛应用于物理、工程、经济等领域的计算中。

格林公式的一般形式如下：$$\oint_C (Pdx + Qdy) = \iint_D ( \frac{{\partialQ}}{{\partial x}} - \frac{{\partial P}}{{\partial y}} ) dA $$其中，$C$表示封闭曲线，$D$表示被封闭曲线围成的区域，$P$和$Q$是$D$内的函数，$\frac{{\partial P}}{{\partial y}}$表示$P$对$y$求偏导数，$\frac{{\partial Q}}{{\partial x}}$表示$Q$对$x$求偏导数，$dA$表示面积元素。

格林公式的应用有以下几个方面：1.计算曲线积分：格林公式将曲线积分转化为了面积积分，使得计算曲线积分更加简便。

通过计算封闭曲线上其中一函数和微分形式 $Pdx + Qdy$ 的积分，可以得到围成该区域的面积。

2.计算平面区域的面积：通过格林公式可以计算出封闭曲线围成的平面区域的面积。

将面积元素 $dA$ 替换为 $1$，$Pdx + Qdy$ 替换为$dx$，然后对曲线积分进行计算，即可得到该区域的面积。

3.计算体积：对于封闭曲线$C$，通过格林公式可以计算出围成该曲线的曲面的面积。

再通过计算该曲面旁切平面上函数的面积积分，就可以得到该曲面的体积。

4.计算电场：格林公式在物理学中应用广泛，特别是在电场计算中。

当电场满足一些条件时，可以通过格林公式计算出电场的其中一参数。

例如，在静电学中，可以通过格林公式计算电场的电势差，从而得到电场的分布。

5.计算流体的流量：格林公式在流体力学中也有重要应用。

通过格林公式，可以计算流体从一个闭合曲面流出的流量，从而得到流体的流速和流量。

格林公式及其应用摘要：本文主要讨论了格林公式及格林定理，格林公式指出了平面区域上二重积分与沿着该区域边界的闭曲线的曲线积分之间的联系，是计算曲线积分重要的公式；而格林定理则说明了积分与路径无关，只与起终点有关。

然后根据格林公式推导出了计算平面区域的面积公式，分别讨论了再（非）闭区域、有奇点存在、平面区域面积的计算、证明质心公式、在物理上关于力场的功的计算以及由格林公式导出的格林函数法用于计算泊松方程和拉普拉斯方程的应用。

关键字：格林公式；格林定理；（非）闭区域；奇点；面积；质心；泊松方程；拉普拉斯方程The Green formula and its applicationAbstract：This paper mainly discusses the Green formula and the Green theorem, Green formula is pointed out between the closed curve in plane area and double integral along the boundary curve of integral relation is important formula curve integral; Green theorem is explained and path independent integral, and the only end point according to the Green formula. According to the Green formula, the formula for calculating the area of the plane is derived. Discussed again (non) closed region, singularity, calculation of plane area, centroid proof in physics calculation formula on stress field work by Green function method and Green formula for calculation of Poisson equation and Laplace equation.Keywords: Green formula; Green Theorem; (non) closed region; singular point; area; barycenter; Poisson equation; Laplace equation1 引言格林公式的多远微积分学中一个重要的公式，它沟通了沿封闭曲线的积分与二重积分之间的联系，给出了平面区域上的二重积分与沿着该区域的边界的闭曲线的曲线积分之间的关系， 2 预备知识2．1格林公式[1]定理1若函数(,)P x y ，(,)Q x y 在闭区域D 上连续，且有连续的一阶偏导数，则有⎰⎰⎰+=∂∂-∂∂DL Qdy Pdxd yP x Q σ)(（1）这里L 为区域D 的边界曲线，分段光滑，并取正方向.（1）式就是格林公式.证 根据区域D 的不同形状，一般可分为三种情形证明：（i ）若区域D 既是x 型区域又是y 型区域，即平行于坐标轴的直线和L 之多交于两点，如图1所示。

第三节格林公式及应用第三节格林公式及应用第三节格林公式及应用3.1自学目标掌握格林公式并会运用平面曲线积分与路径无关的条件，会求二元函数全微分的原函数.3.2内容提要1.格林公式设闭区域d由分段扁平的曲线l围起，函数p?x,y?,q?x,y?在d内具备一阶已连续略偏导数，则存有q?p?pdx?qdy?dxdy，lx?y?d?其中l是d的取正向的边界曲线．【备注】（1）格林公式阐明了二重积分与曲线分数的联系．（2）d可以就是为丛藓科扭口藓相连区域．（3）l为正向的封闭曲线，p?x,y?,q?x,y?在d内具有一阶连续偏导数，两者缺一不可．在利用格林公式计算曲线积分时，若l不封闭，则考虑适当补边使之封闭；若在d内函数有奇点，应考虑将奇点挖掉．（4）当p??y,q?x时，纡出来半封闭曲线所围区域的面积a?1xdy?ydx??l22.平面上曲线积分与路径无关的条件设立区域g就是一个单相连域，函数p?x,y?,q?x,y?在区域g内具备一阶已连续的偏导数，则曲线分数必须条件就是pdxqdy在g内与路径无关（或沿g内任意闭曲线的曲线积分为零）的充l?q?p??x?y在g内恒设立．【注】若曲线积分与路径无关，在进行曲线积分的计算时，可以在g内选择简单路径，选择折线是常用的方法．3.二元函数的全微分算草设区域g是一个单连通域，函数p?x,y?,q?x,y?在区域g内具有一阶连续的偏导数，则p(x,y)dx?q(x,y)dy在g内为某一函数u(x,y)的全微分的充要条件是qpxy在g内恒设立．(x,y)xyu(x,y)??或(x0,y0)p(x,y)dx?q(x,y)dy??p(x,y0)dx??q(x,y)dyx0y0yxu(x,y)??q(x0,y)dy??p(x,y)dx．y0x0其中m0(x0,y0)就是区域g内适度选取的一点．【注】设区域g是一个单连通域，函数p?x,y?,q?x,y?在区域g内具有一阶连续的偏导数，则以下四个命题等价：命题1曲线分数pdxqdy在g内与路径无关；l命题2在g内任一一条闭合曲线l，存有pdxqdy=0；l命题3表达式p?x,y?dx?q?x,y?dy在g内就是某个二元函数的全微分，即为存有u?x,y?使得du?p?x,y?dx?q?x,y?dy；命题4qp在g内每一点处成立．?x?yl4.计算pdxqdy的通常步骤qp，?x?y（1）首先验证是否（2）若qp，考察l是否封闭，若封闭用格林公式；?x?y??xt?,t求，若不封闭取参数?y??t,（3）若来求．qp，也实地考察l与否半封闭，若半封闭结果为0；若不半封闭，用折线或用补线?x?y3.3典型例题与方法基本题型i：利用格林公式谋第二类曲线分数基准1填空题x22(1)设f(x,y)在d:?y?1内具有连续的二阶偏导数，c为顺时针方向的椭圆4x2?y2?1，则??c[?3y?fx'(x,y)]dx?fy'(x,y)dy?________．42?2f??xyi?xyj促进作用下沿圆周x2?y2?a2的顺时针方向运动一周，(2)设立质点在力则力f所作的功w?________．求解（1）由格林公式，注意到曲线c为顺时针方向，得[?3y?f'(x,y)]dx?f'(x,y)dy[f\x,y)?f''(x,y)?3]d?3d?6?cxyyxxydd故应填?6?．222（2）设曲线c:x?y?a围成的区域为d，则2?a1422223wxydx?xydy??(x?y)dxdy??d??d?a?c?002d14故应填??a．2例2选择题22（1）设立曲线c为椭圆4x?y?1，并挑正向，则曲线分数??c?ydx?xdy等同于（）.4x2?y2（a）0；（b）2?；（c）??；（d）?．（2）已知xaydxydy就是某函数的全微分，则a等同于（）.2?x?y?（a）?1；（b）0；（c）?2；（d）2．22解（1）因为4x?y?1，代入得ydxxdy2dxdy．??c4x2?y2c?ydx?xdyd故挑选（d）．（2）p(x,y)?x?ay?x?y?,q(x,y)?2y?x?y?2,于是p(a2)xayq2y,,33yxxyxypq由可得a?2，故选（d）．?y?xx2y2例3计算??x?y?dx??x?y?dy，其中l为椭圆线2?2?1的正向.lab【分析】l为半封闭扁平曲线挑正向，合乎格林公式的条件，需用格林公式展开排序.求解x?y?dxx?y?dy=1?1?dxdy2dxdy2?ab，lddx2y2其中d为椭圆域2?2?1.ab例4计算x?y?dxx?y?dyx?y22l，其中l为圆x2?y2?a2的正向.【分析】此题可直接用公式x?acost,y?asint,0?t?2?计算.也可用积分曲线方程化简被积函数，再用格林公式计算．下面给出后一种解法.求解l?x?y?dxx?y?dy?x2?y21a2l?x?y?dxx?y?dya21?1?d?d??2?a2??2?.2a222【方法点击】该题不能直接利用格林公式计算，因为被积函数在d:x?y?a内不满足具有一阶连续偏导数的条件，但由曲线l的方程化简被积函数后，就满足了格林公式的条件，可再用格林公式计算.基准5排序3x2x?是半圆弧.(ye?my)dx?(3ye?m)dy,c为从e到f再到g,fg?cyf(2,1)oe(1,0)g(3,0)x图3-1【分析】似乎c为从e至g的分段扁平曲线，可以轻易化成的定分数展开排序，但排序较繁杂．如果补边ge，则可以沦为半封闭曲线，利用格林公式排序后再乘以ge上的分数，可以得所求分数值．但必须特别注意曲线的方向．pq3y2exm,3y2ex,解p?ye?my,q?3ye?m,?y?x3x2x?q?p??m.添加直线ge,利用格林公式得，?x?y?c(y3ex?my)dy?(3y2ex?m)dy+?pdx?qdy??gemdxdy??m(1?)．??4d??所以,c(y3exmy)dy(3y2exm)dy=(1)m-gepdxqdy=m(1).44【方法点击】补边是利用格林公式解决非封闭曲线积分的重要方法，但须满足格林公式的条件．例6计算段.2l?ydx?xdy，其中沿曲线自点?2,0?至?0,0?的存有向弧y?2x?x?ly图3-2ox【分析】本题可利用l的方程直接求解，得到解法一．还可以通过补边，使其满足格林公式的条件，再利用格林公式计算.数学分析一如图3-2右图，l的方程y?2x?x2,dy?0?1?x2??ydx?xdy??2x?x?x??l?2?2x?x2?1?x2x?x2dx，故dx.数学分析二补线l1:?由格林公式0x2（方向与x轴的方向一致），l1与曲线l围成闭区域d，y?0ydx?xdy??ll?l1?ydx?xdyydx?xdyl1而q?p?ydx?xdyl?l1xydxdy?2dxdy.dd从而l1ydxxdy0.ydx?xdy.l。

格林公式及其应用步骤与注意事项1．格林公式当(1)积分曲线为闭曲线L；(2)积分曲线L的方向相对于其围成的封闭区域D以左手法则判定为正方向；(3)在闭区域上，两个二元函数P(x,y)和Q(x,y)存在有一阶连续偏导数，则有【注1】正确使用以上标准格林公式，三个条件：闭曲线、正方向、闭区域上的偏导连续性，一个都不能少。

【注2】格林公式中闭区域的边界曲线不取由左手法则确定的正向，而是取相反的方向时，则借助于对坐标的曲线积分的方向性计算性质，有即不管边界曲线取什么方向，有利用“左手法则”判断为正方向，则取正；否则取负。

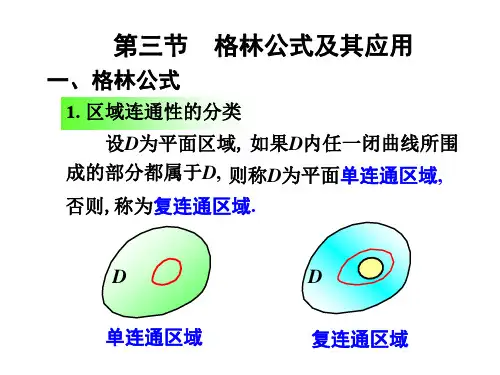
【注3】判断平面区域的边界曲线正向的“左手法则”：当沿着边界曲线的正方向行走时，平面区域应该位于我们左手一侧，所以对于单连通区域，即只有外边界曲线的实心区域来说，曲线的正方向为逆时钟方向；对于多连通区域，则边界曲线由内外边界曲线构成，外边界曲线的正方向为逆时钟方向，内边界的边界曲线为顺时钟方向。

【注4】注意封闭曲线切向量方向与外法线方向的关系。

如果切向量方向为T0=(cosα,cosβ)（T=(x’(t),y’(t))），则当曲线的切向量指向为逆时钟方向时，则外法线方向的方向向量为n0=(cosβ,-cosα)（n=(y’(t),-x’(t))）；当曲线的切向量指向为顺时钟方向时，则外法线方向的方向向量为n0=(-cosβ,cosα)（n=-(y’(t),-x’(t))）。

即曲线的法向量与切向量的关系为：n=±(y’(t),-x’(t))。

取正号时，法向量为切向量顺时钟旋转90度得到；取负号时，法向量为切向量逆时钟旋转90度得到。

2．利用格林公式计算对坐标的曲线积分的基本思路与步骤依据以上定理，有如下使用格林公式计算关于平面上的积分曲线对坐标的曲线积分计算步骤：第一步：明确被积表达式中的P(x,y)和Q(x,y)函数(dx前面的函数为P(x,y)，dy前面的函数为Q(x,y)，如果有负号，记得带上负号)。