当前位置：文档之家 › 第4章 轴心受力构件例题分解

第4章 轴心受力构件例题分解

  • 格式：ppt
  • 大小：1.46 MB
  • 文档页数：41

下载文档原格式

  / 41

合集下载

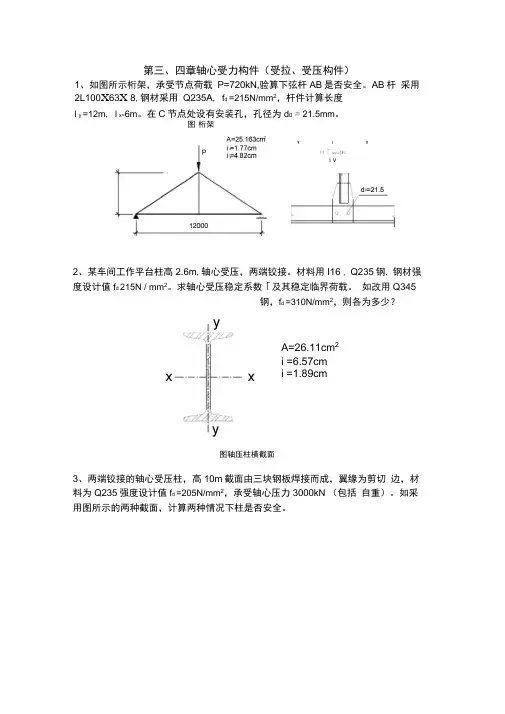
四章轴心受力构件

四章轴心受力构件

第三、四章轴心受力构件（受拉、受压构件）1、如图所示桁架，承受节点荷载 P=720kN,验算下弦杆AB 是否安全。

AB 杆 采用2L100X 63X 8,钢材采用 Q235A , f d =215N/mm 2，杆件计算长度l °y =12m , l °x =6m 。

在C 节点处设有安装孔，孔径为d 0 = 21.5mm 。

2、某车间工作平台柱高2.6m ,轴心受压，两端铰接。

材料用I16 , Q235钢, 钢材强度设计值f d 215N / mm 2。

求轴心受压稳定系数「及其稳定临界荷载。

如改用Q345钢，f d =310N/mm 2，则各为多少？A=26.11cm 2i =6.57cm i =1.89cm图轴压柱横截面3、两端铰接的轴心受压柱，高10m 截面由三块钢板焊接而成，翼缘为剪切 边，材料为Q235强度设计值f d =205N/mm 2，承受轴心压力3000kN （包括 自重）。

如采用图所示的两种截面，计算两种情况下柱是否安全。

图 桁架YIVF f『 求求 J | F Ai yI x i! 8----------- 1—— ---了 0y 1-^—■_1—V -iXi x20 500 : ---------------------.20yiyi 单肢(a)(b)图轴压柱横截面4、验算一轴心受压缀板柱。

柱肢采用工字型钢，如图所示。

已知轴心压力设 计值N=3000kN （包括自重），计算长度l °x=20m , l °y=10m （x 轴为虚轴），材料为Q235，强度设计值f d =205N / mm 2，仏=125N/mm 2。

5、有一拔杆，采用Q235钢，f d =215N/mm 2，如图5-9所示，缀条采用斜杆 式体系。

设考虑起吊时的动力作用等，应将起重量乘以 1.25,并设平面内、外 计算长度相等。

问'=60°时，拔杆最大起重量设计值为多少？zlmrnu04I A I* 45°iI [I 拔杆截面尺寸r图拔杆横截面及受力示意图。

轴心受力构件

轴心受力构件

第4章 轴心受力构件例题 4.1 某焊接组合工字形截面轴心受压构件的截面尺寸如图4-13所示，承受轴心压力设计值(包括构件自重)N ＝2000kN ，计算长度l 0y ＝6m ，l 0x ＝3m ，翼缘钢板为火焰切割边，钢材为Q345，截面无削弱。

要求验算该轴心受压构件的整体稳定性是否满足设计要求，并计算整体稳定承载力。

图4—13 焊接工字形截面解 （1）截面及构件几何特性计算A =250×12×2+250×8=8000mm 2I y =(250×2743-242×2503)/12=1.1345×108 mm 4 I x =(12×2503×2+250×83)/12=3.126×107 mm 41.1198000/101345.1/8=⨯==A I i y y mm5.628000/10126.3/7=⨯==A I i x x mmλy =l 0y /i y =6000/119.1=50.4 λx =l 0x /i x =3000/62.5=48.0 (2)整体稳定性验算查表4－5，截面关于x 轴和y 轴都属于b 类，λy >λx1.61235/3454.50235/==y y f λ查附表7得φ=0.80169.31180008016.01020003=⨯⨯=A N ϕN/mm 2≈f =310N/ mm 2 故可认为整体稳定性满足要求。

（3）整体稳定承载力计算φAf =0.8016×8000×310=1.988×106N=1988kN 该轴心受压构件的整体稳定承载力为1988kN 。

例题4.2 某焊接T 形截面轴心受压构件截面尺寸如图4—14所示。

承受轴心压力设计值(包括构件自重)N ＝2000kN ，计算长度l 0x ＝l 0y ＝3m ，翼缘钢板为火焰切割边，钢材为Q345，截面无削弱。

4-钢结构设计原理-轴心受力构件1 钢结构设计原理

4-钢结构设计原理-轴心受力构件1 钢结构设计原理
第四章 轴心受力构件
4 轴
主要内容:
心
受 力
1、轴心受拉构件的强度和刚度
构
件 设
2、轴心受压构件的强度
计
3、轴心受压实腹式构件的整体稳定
4、轴心受压格构式构件的整体稳定
5、轴心受压实腹式构件的局部稳定
6、轴心受压格构式构件的局部稳定
7、轴心受力构件的刚度
学习目标
1.掌握轴心受拉构件强度的计算方法、净截面的概念；
4
轴
心 受
所谓分支点失稳，是指当荷载逐渐增加到某一数值
力 构
时，结构除了按原有变形形式可能维持平衡之外，还可
件 设
能以其他变形形式维持平衡，这种情况称为出现平衡的
计
分支。出现平衡的分支是此种结构失稳的标志。
对于受偏心压力的细长直杆，当荷载逐渐增大而趋
于某一数值时,其原有变形形式急剧增大，致使结构丧
失承载能力。这种失稳现象称为极值点失稳。
结构或构件在外力增加到某一数值时，稳定的平衡
状态开始丧失，稍有扰动，结构变形迅速增大，使结构 丧失正常工作的能力，称为失稳。
在桥梁结构中，总是要求沿各个方向保持稳定的平
衡，也即沿各个方向都是稳定的，避免不稳定的平衡或 随遇平衡。
结构稳定问题的两种形式：
第一类稳定问题，分支点失稳问题； 第二类稳定问题，极值点失稳问题。
4
轴 心 受 力 构 件 设 计
4.3.3轴压稳定理论的沿革——具有初始缺陷的实际轴心压杆的稳 定问题
有关轴心压杆的整体稳定问题的理论经历了由理想状态杆件的
单曲线函数关系到实际状态杆件多曲线函数关系的沿革。传统的
理想状态压杆的单曲线稳定理论认为轴压杆是理想状态的，它在

轴心受力构件部分公式及例题

轴心受力构件部分公式及例题
满足整体稳定性要求。 满足整体稳定性要求。 其整体稳定承载力为： 其整体稳定承载力为：
N c = ϕAf = 0.802 × 8000 × 315 = 2020000 N = 2020 kN
钢结构原理 Principles of Steel Structure
第四章
轴心受力构件
某焊接T形截面轴心受压构件的截面尺寸如右图所示 形截面轴心受压构件的截面尺寸如右图所示， 例4.2 某焊接 形截面轴心受压构件的截面尺寸如右图所示， 承受轴心压力设计值（包括自重） 承受轴心压力设计值（包括自重）N=2000kN，计算长度 ， l0x=l0y=3m，翼缘钢板为火焰切割边，钢材为 ，翼缘钢板为火焰切割边，钢材为Q345， ， f=315N/mm2，截面无削弱，试计算该轴心受压构件的整体 截面无削弱， 稳定性。 稳定性。
(
)
λz =
=
Iω
2 Ai0 2 lω + I t 25.7
y
-250×8 ×
80 × 180.7 = 45.2 2 536500 300 + 28.7 25.7
x
x
λz < λ y，λx
故该构件由弯曲屈曲控制设计。 故该构件由弯曲屈曲控制设计。
钢结构原理 Principles of Steel Structure
-250×8 ×
x
x
y -250×12 ×
钢结构原理 Principles of Steel Structure
第四章 1、截面及构件几何性质计算 、
截面面积 惯性矩： 惯性矩：
轴心受力构件
A = 250 × 12 × 2 + 250 × 8 = 8000mm 2 1 I x = ( 250 × 2743 − 242 × 2503 ) = 1.1345 × 108 mm 4 12 1 I y = (12 × 2503 × 2 + 250 × 83 ) = 3.126 × 107 mm 4 y 12

(钢结构设计原理)第四章 轴心受力构件

(钢结构设计原理)第四章 轴心受力构件
(3)1990年2月16日我国大连重型机械厂14.4m的轻钢屋架 重盖会议室在305人开会时塌落（设计时计算长度取错 ），造成42人死亡和179人受伤（46人重伤）。
•梭形轻型钢屋架设计上误算。 •施工中屋面重量过量增加。施工单位没有完全按图纸施工，改设了 屋面干铺炉渣保温层，违反国家颁发的《建筑安装工程施工验收技术 规范》；加厚了水泥砂浆找平层，增加了屋面荷重，加速了钢屋架的 破坏。 •建设单位管理混乱。
cr22Efp或长:细 p比 fE P
只有长细比较大（≥p）的轴心受压构件，才能满足上式的要求。 对于长细比较小（<p）的轴心受压构件，截面应力在屈曲前已经 超过钢材的比例极限，构件处于弹塑性阶段，应按弹塑性屈曲计算 其临界力。
2020/12/12
无缺陷轴心受压构件的弹塑性弯曲失稳
无缺陷轴心受压构件的弹塑性弯曲失稳
截面为单轴对称（T形截面）的轴心受压构件绕对称轴失稳时，由于截 面形心和剪切中心不重合，在发生弯曲变形的同时必然伴随有扭转变 形，这种现象称为弯扭失稳。
2020/12/12
轴心受压构件的整体失稳状态
轴心受压构件的整体失稳状态
a)弯曲屈曲
2020/12/12
b)扭转屈曲
轴心受压构件的整体失稳的例子
c)弯扭屈曲
2020/12/12
广州新白云国际机场航站楼柱子
轴心受压构件的整体失稳的例子
2020/12/12
铸钢节点长细比
轴心受压构件的整体失稳的例子
2020/12/12
无缺陷轴心受压构件的整体失稳
无缺陷轴心受压构件的整体失稳
理想轴心受压构件 （1）杆件为等截面理想直杆； （2）压力作用线与杆件形心轴重合； （3）材料为匀质，各向同性且无限弹性，符合虎克定律； （4）构件无初应力，节点铰支。

第四章轴心受力构件解剖

第四章轴心受力构件解剖

取n 1，得：kl 即：k 2 2 l 2
Ncr Ncr
因：k 2
N cr
2
EI 1 N cr l 2
GA
故，临界力N cr：
2 EI
1
N cr l 2 2 EI
1
l 2 GA
临界应力 cr：
cr
N cr A
2E
1
2
1
2 EA
2
GA
(4 3) (4 4)
1、理想轴心压杆的整体稳定 （欧拉临界力 ）
0
图 4-6 有初弯曲和初偏心的轴压杆图
v 4-9 轴心压杆的压力－挠度曲线
【例 4-2】 验算如图 4-11(a)所示结构中两端铰接的轴心受压柱 AB 的整体稳定。柱所承受的压力设计值N =1000kN，柱的长度为 4.2 m。 在柱截面的强轴平面内有支撑系统以阻止柱的中点在 ABCD 的平面内 产生侧向位移，见图 4-11(a)。柱截面为焊接工字形，具有轧制边翼 缘，其尺寸为翼缘 2—1 0×2 20，腹板 1—6×200，见图 4-11(b)。 柱由 Q235 A 钢制作。
直接承受动 力荷载的结构
250
项次 1 2
表 4-2 受压构件的容许长细比 构件名称
柱、桁架和天窗架中的杆件 柱的缀条、吊车梁或吊车桁架以下的柱间支撑 支撑（吊车梁或吊车桁架以下的柱间支撑除外）
用以减少受压构件长细比的杆件
容许长细比 150 200
二、轴心受压构件的整体稳定
图 4-4 轴心压杆的屈曲变形 （a） 弯曲屈曲；(b) 扭转屈曲；(c)弯扭屈曲
第四章 轴心受力构件
一、轴心受力构件的强度和刚度 二、轴心受压构件的整体稳定 三、轴心受压构件的局部稳定 四、实腹式轴心受压柱的设计 五、格构式轴心受压构件的截面设计 六、轴心受压柱的柱头和柱脚

轴心受力构件部分公式及例题

轴心受力构件部分公式及例题

x
y -250×12
钢结构原理 Principles of Steel Structure
第四章 轴心受力构件
1、截面及构件几何性质计算
截面面积 惯性矩：
A 2 5 0 1 2 2 2 5 0 8 8 0 0 0 m m 2
Ix 1 1 22 5 0 2 7 4 3 2 4 2 2 5 0 3 1 .1 3 4 5 1 0 8 m m 4 Iy 1 1 21 2 2 5 0 3 2 2 5 0 8 3 3 .1 2 6 y1 0 7 m m 4
第四章 轴心受力构件
例4.1 某焊接组合工字形截面轴心受压构件的截面尺寸如图 所示，承受轴心压力设计值（包括自重）N=2000kN，计算 长度l0x=6m ，l0y=3m，翼缘钢板为火焰切割边，钢材为Q345， f=315N/mm2，截面无削弱，试计算该轴心受压构件的整体稳 定性。
y
-250×8
x
由于热轧H 型钢可以选用宽翼缘的形式，截面宽度较大，因 而长细比的假设值可适当减小，假设=60，对宽翼缘H型钢因 b/h>0.8，所以不论对x轴或y轴均属类b截面。
fy 60
235
需要的截面几何量为
查附表得
0.8 0 7
A N f 0.810 62 7 01 1 0 3 0 1 52 09.2cm 2
惯性矩：
Ix11 22502432502434.25211 282503
2508(12522.25)23.886107m m 4
Iy 1 1 22 4 2 5 0 3 2 5 0 8 3 3 .1 2 6 1 0 7 m m 4
钢结构原理 Principles of Steel Structure

4钢筋混凝土轴心受力构件

4钢筋混凝土轴心受力构件

N 0 ( G N gk Q C Nqk ) 1.1 (1.351851.4 0.7 70) 350.2kN

N 35210 2 As 1173 mm fy 300
3

【解】（3）满足构造要求的配筋
As min 0.4% A 0.4% 200 250 200m m2 As min
在截面尺寸、配筋、强度相同的条件下，长 柱的 承载力低于短柱，(采用降低系数来考虑)
三、轴心受压构件的受力分析
1. 短柱
钢筋屈 服
混凝土压碎
h
N
As
N
b
Hale Waihona Puke ANol
混凝土压碎
钢筋凸出
第一阶段：加载至钢筋屈服 第二阶段：钢筋屈服至混凝土压碎
三、轴心受压短柱的受力分析
1. 短柱
平衡方程 变形协调方程

轴心受力构件 (a) 轴心受拉； (b) 轴心受压；
工程实例
压 压 拉 压
拉
多层房屋的内柱
第一节、轴心受拉构件的受力特点
1. 受拉构件的配筋形式
纵筋
h
箍筋
b
纵筋
第一节、轴心受拉构件的受力特点
2. 试 验 研 究
N N
Ncr
箍筋
Ncr
Nc
Nc
第一节、轴心受拉构件的受力特点
2. 试 验 研 究
先选用直径较小的钢筋。
第二节、轴心受拉构件的承载力计算
3. 例 题

【例4.1】某钢筋混凝土屋架下弦，其截面尺寸 为b×h=140mm×140mm，混凝土强度等级为 C30，钢筋为HRB335级，承受轴向拉力设计值 为N=200kN，试求纵向钢筋截面面积As。 【解】由式(4-11)得 As=N/fy=666.67mm2 配置4Φ16(As=806mm2)

《钢结构原理》第4章轴心受力构件

《钢结构原理》第4章轴心受力构件

2tb3
3 12 12
2E k3 y2
crx
2E Iex x2 Ix
2E 2t kb h2
x2
2tbh2 4
4
2E
k
x2
2021/8/30
26
《钢结构原理》 第4章 轴心受力构件
4.4.4.2 初弯曲的影响
假设构件变形 为正弦曲线：
y0
v0
sin
x
l
v0为初始挠度
2021/8/30
x
l0x ix
,
y
l0 y iy
l0x，l0y —— 构件的计算长度； ix，iy —— 截面回转半径； [] —— 容许长细比。
2021/8/30
9
《钢结构原理》 第4章 轴心受力构件
2021/8/30
10
《钢结构原理》 第4章 轴心受力构件
【例题】 某钢屋架下弦采用L125×12双角钢做成，钢材为 Q235，截面无削弱，计算长度为12.2m，承受静力荷载设计值 为900kN，要求验算此拉杆的强度和刚度。
后存在加压和减压区）
2021/8/30
21
《钢结构原理》 第4章 轴心受力构件
4.4.4 影响轴心受压构件整体稳定承载力的因素
理想等直杆是不存在的，实际工程中的轴心受压 构件有很多几何缺陷和力学缺陷，其中影响稳定承载 力的主要因素有：
截面的纵向残余应力 构件的初始弯曲 荷载作用点的初偏心 构件端部的约束条件
N A
Nv0
W 1 N
NE
fy
假设 v0= l / 1000，则上式整理可得：
N A
1
1000
i
1
1 N
N

第四章 轴心受力构件

第四章 轴心受力构件

第四章轴心受力构件§4-1 概述1、工程实例（假设节点为铰接，无节间荷载作用时，构件只受轴心力作用）（1）桁架（2）塔架（3）网架、网壳2、分类⑴按受力来分：①轴心受拉构件②轴心受压构件到某临界值时，理想轴心受压构件可能以三种屈曲形式丧失稳定。

(1) 弯曲屈曲构件的截面只绕一个主轴旋转，构件的纵轴由直线变为曲线，这是双轴对称截面构件最常见的屈曲形式。

如图4-2 (a)就是两端铰接工字形截面构件发生的绕弱轴的弯曲屈曲。

(2) 扭转屈曲失稳时构件除支承端外的各截面均绕纵轴扭转，图4-2 (b)为长度较小的十字形截面构件可能发生的扭转屈曲。

(3) 弯扭屈曲单轴对称截面构件绕对称轴屈曲时，在发生弯曲变形的同时必然伴随着扭转。

图4-2 (c)即T 形截面构件发生的弯扭屈曲。

图4-2 轴心受压构件的三种屈曲形式欧拉临界力和欧拉临界应力临界应力其中：——单位剪力时的轴线转角，；通常剪切变形的影响较小，忽略其对临界力或临界应力的影响。

E N E σ1222211γλπλπσ⋅⋅+⋅⋅==EAEAN cr cr1γ)(1GA βγ=这样，※上述推导基于材料处于弹性阶段，即，或。

（二）初始缺陷对轴心受压构件稳定承载力的影响 1. 残余应力的影响残余压应力对压杆弯曲失稳的影响： 对弱轴的影响比对强轴的影响要大的多。

稳定应力上限，弱轴：强轴：其中：，0＜＜1.0。

2．初弯曲的影响图4-3 考虑初弯曲的压力—挠度曲线图示压力—挠度曲线有如下特点：1有初弯曲时，挠度v 不是随着N 按比例增加；N 较小时，挠度增加较慢，N 趋于时，挠度增加较快，并趋向于无限大；2相同压力N 的作用下，压杆的初挠度值越大，杆件的挠度也越大；Ecr N EAlEI N =⋅=⋅=2222λππEcr cr E AN σλπσ=⋅==22pcr f E≤⋅=22λπσpp f E λπλ=≥322kEx crx ⋅⋅=λπσkEycry⋅⋅=22λπσ翼缘宽度翼缘弹性区宽度=k k E N3由于有的存在，轴心压杆的承载力总是低于，因此是弹性压杆承载力的上限。

第4章 轴心受力构件例题分解

第4章 轴心受力构件例题分解
柱肢近似作为桁架的弦杆，按轴心受压杆件设计,其整体稳定计算 数值（N mm2 ）与（）最接近。 提示：按b类截面查轴心压杆稳定系数。 （A）191.5 （C）163.1 （B）179.2 （D）214.3
例4.3图
答案（A） 主要作答过程：
y
N 2698 103 191.5 N mm2 205 N mm2 y A 0.75118760
N 1000 103 A 6190mm2 61.9cm2 y f 0.751 215
选用2［22a， iy 8.67cm A 63.6cm2 ，
。
验算整体稳定性：
y
l0 y iy

600 69.2 [ ] 150 8.67
查表得 y 0.756
2 f 215 N / mm iy 4.52cm ，
，角钢的厚度为10mm,在
确定危险截面之前先把它按中面展开如图5.9(b)所示。 正交净截面的面积为： An 2 (4.5 10 4.5 2) 1.0 34.0cm2 齿状净截面的面积为：
An 2 (4.5 10 2 42 4.5 2 2) 1.0 31.5cm 2
整体稳定和刚度验算。
长细比：
l0 x 600 x 27.3 [ ] 150 ix 22.0 300 y 94.3 [ ] 150 iy 3.18 l0 y
y 远大于 x ，故由 y 查附表4.2得 0.591 。
N 1600 103 2 2 200.5N / mm f 205N / mm A 0.591135 102
N 1000 103 2 2 208N / mm f 215N / mm y A 0.756 63.6 102

钢结构4章例题分析

钢结构4章例题分析

3.焊接工字形截面[图4.21(d)] (1)试选截面 参照H型钢截面，选用截面如图5.15(d)所示，翼缘2
－250×14，腹板1－250×8，其截面面积：
设计原理
钢结构
A 2 25 1.4 25 0.8 90cm 1 I x (25 27.83 24.2 253 ) 13250cm 4 12
长细比：
l0 x 600 x 27.3 [ ] 150 ix 22.0 300 y 94.3 [ ] 150 iy 3.18 l0 y
y 远大于 x ，故由 y 查附表4.2得 0.591 。
设计原理
钢结构
第四章 轴心受力构件例题
N 1600 103 2 2 200.5N / mm f 205N / mm A 0.591135 102
N An f 31.5102 215 677250N 677kN
容许的最大计算长度为： 对x轴，
lox [ ] ix 350 30.5 10675mm
对y轴，
loy [] iy 350 45.2 15820mm
设计原理
钢结构
【例4.2】图4.21(a)所示为一管道支架，其支柱的设计 第四章 轴心受力构件例题
An 2 (4.5 10 4.5 2) 1.0 34.0cm2
齿状净截面的面积为：
设计原理
钢结构
An 2 (4.5 10 2 42 4.5 2 2) 1.0 31.5cm 2
第四章 轴心受力构件例题
危险截面是齿状截面，此拉杆所能承受的最大拉力为：
2.热轧H型钢 (1)试选截面[图4.21(c)] 由于热轧H型钢可以选用宽翼缘的形式，截面宽度 较大，因此长细比的假设值可适当减小，假设 60 。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 f 215 N / mm iy 4.52cm ，
，角钢的厚度为10mm,在
确定危险截面之前先把它按中面展开如图5.9(b)所示。 正交净截面的面积为： An 2 (4.5 10 4.5 2) 1.0 34.0cm2 齿状净截面的面积为：
An 2 (4.5 10 2 42 4.5 2 2) 1.0 31.5cm 2
N 1600 103 2 A 92.2cm f 0.807 215 102 600 10.0cm 60 l0 y 300 iy 5.0cm 60 ix l0 x
由附表7.2中试选 HW250×250×9×14,
A 92.18cm , ix 10.8cm, iy 6.29cm
整体稳定和刚度验算。
长细比：
l0 x 600 x 27.3 [ ] 150 ix 22.0 300 y 94.3 [ ] 150 iy 3.18 l0 y
y 远大于 x ，故由 y 查附表4.2得 0.591 。
N 1600 103 2 2 200.5N / mm f 205N / mm A 0.591135 102
【例4.2】图(a)所示为一管道支架，其支柱的设计压力 为N=1600kN(设计值)，柱两端铰接，钢材为Q235,截面
无孔眼削弱。试设计此支柱的截面：①用普通轧制工字
钢；②用热轧H型钢；③用焊接工字形截面，翼缘板为 焰切边。
【解】 支柱在两个方向的计算长度不相等,故取如图4.21(b) 所示的截面朝向，将强轴顺X轴方向,弱轴顺Y轴方向。这 样，柱在两个方向的计算长度分别为：
A 2 25 1.4 25 0.8 90cm 1 I x (25 27.83 24.2 253 ) 13250cm 4 12
2
1 1.4 253 3650cm 4 12 13250 ix 12.13cm 90 Iy 2 3650 iy 6.37cm 90
(2)整体稳定和长细比验算
长细比： x l0 x 600 49.5 [ ] 150 ix 12.13
300 y 47.1 [ ] 150 iy 6.37 l0 y
因对x轴和y轴
值均属于b类,故由长细比的较大值
。
0.859 查附表4.2得
N 1600 103 2 2 207N / mm f 215N / mm A 0.859 90 102
2.热轧H型钢 (1)试选截面[图 (c)] 由于热轧H型钢可以选用宽翼缘的形式，截面宽度 较大，因此长细比的假设值可适当减小，假设 60 。
对宽翼缘H型钢，因b / h 0.8 ，所以不论对x轴或y轴
都属于b类截面，当 60 时，由附表4.2查得 0.807 ， 所需截面几何量为：
危险截面是齿状截面，此拉杆所能承受的最大拉力为：
N An f 31.5102 215 677250N 677kN
容许的最大计算长度为： 对x轴，
lox [ ] ix 350 30.5 10675mm
对y轴，
loy [] iy 350 45.2 15820mm
lox 600cm; loy 300cm
1. 轧制工字钢[图 (b)]
(1)试选截面
假定 90 ，对于轧制工字钢，当绕x轴失稳时属 于a类截面，由附表4.1查得 x 0.714 ;绕y轴失稳时属 于b类截面，由附表4.2查得 y 0.621 。
(2) 截面验算 因截面无孔眼削弱，可不验算强度。又因轧制工字 钢的翼缘和腹板均较厚，可不验算局部稳定，只需进行
x 55.6
查表得
。 0.83
N 1600 103 2 2 209N / mm f 215N / mm A 0.83 92.18 102
3.焊接工字形截面[图 (d)] (1)试选截面 参照H型钢截面，选用截面如图5.15(d)所示，翼缘2
－250×14，腹板1－250×8，其截面面积：
第4章 例题
【例4.1】图4.9示一有中级工作制吊车的厂房屋架的双
角钢拉杆，截面为2┗100×10，角钢上有交错排列的普
通螺栓孔，孔径 d＝200mm。试计算此拉杆所能承受的 最大拉力及容许达到的最大计算长度。钢材为Q235钢。
【解】 查型钢表附表7.4， 2∠100×10角钢，ix 3.05cm ，
因腹板高厚比小于80，故不必设置横向加劲肋。翼缘 与腹板的连接焊缝最小焊脚尺寸为：
hf min 1.5 t 1.5 14 5.6mm
hf 6mm
采用
。
【例4.3】（注册结构师考题题型）
封闭式通廊的中间支架如图4.22所示，通廊和支架均采用钢结 构,材料为Q235B钢,焊条采用E43型。支架柱肢的中心距为7m和4m， 支架的交叉腹杆按单杆受拉考虑。 （1）已知支架受压柱肢的压力设计值N=26989kN，柱肢采用热轧 22 H型钢HW394×398×11×18， A A 18760mm 18760mm ,, ii 173mm 173mm, iy 100mm 12.5 235 8.9 (10 0.1 ) 14.95 t 1.4 fy
腹板的局部稳定：
h0 25 235 31 .25 (25 0.5 ) 49.75 tw 0.8 fy
截面无孔眼削弱，不必验算强度。 (4)构造
2
(2) 截面验算 因截面无孔眼削弱，可不验算强度。又因轧制工字钢 的翼缘和腹板均较厚，可不验算局部稳定，只需进行整体 稳定和刚度验算。
长细比：
l0 x 600 x 55.6 [ ] 150 ix 10.8 l0 y
300 y 47.7 [ ] 150 iy 6.29 因对x轴和y轴 值均属于b类，故长细比的较大值