学而思九年级数学教材[精品文档]

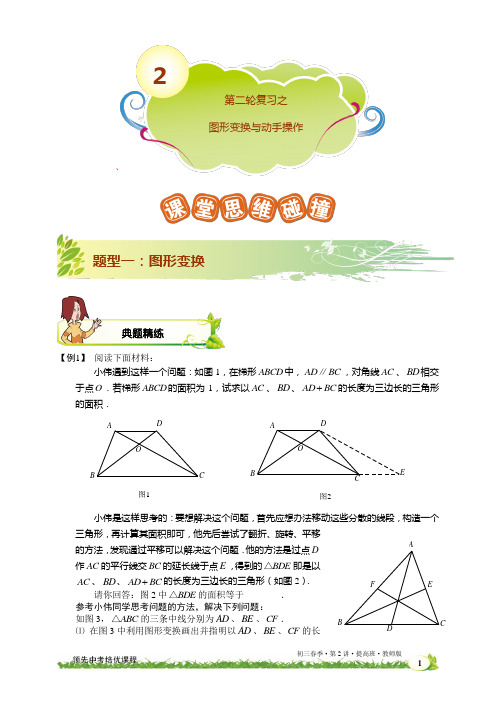
`【例1】 阅读下面材料：小伟遇到这样一个问题：如图1，在梯形ABCD 中，AD BC ∥，对角线AC 、BD 相交于点O ．若梯形ABCD 的面积为1，试求以AC 、BD 、AD BC +的长度为三边长的三角形的面积．图1图2ADBCOADBCOE小伟是这样思考的：要想解决这个问题，首先应想办法移动这些分散的线段，构造一个三角形，再计算其面积即可，他先后尝试了翻折、旋转、平移的方法，发现通过平移可以解决这个问题．他的方法是过点D 作AC 的平行线交BC 的延长线于点E ，得到的BDE △即是以AC 、BD 、AD BC +的长度为三边长的三角形（如图2）． 请你回答：图2中BDE △的面积等于________． 参考小伟同学思考问题的方法，解决下列问题：如图3，ABC △的三条中线分别为AD 、BE 、CF ．⑴ 在图3中利用图形变换画出并指明以AD 、BE 、CF 的长典题精练2第二轮复习之 图形变换与动手操作题型一：图形变换图3AFE CD B度为三边长的一个三角形（保留画图痕迹）；⑵ 若ABC △的面积为1，则以AD 、BE 、CF 的长度为三边长的三角形的面积等于________．（2011北京）【解析】BDE △的面积等于 1 .⑴ 如图.以AD 、BE 、CF 的长度为三边长的一个三角形是CFP △. ⑵ 以AD 、BE 、CF 的长度为三边长的三角形的面积等于34. 【例2】 阅读下面材料：小明遇到这样一个问题：我们定义: 如果一个图形绕着某定点旋转一定的角度α (0︒ <α <360︒) 后所得的图形与原图形重合，则称此图形是旋转对称图形. 如等边三角形就是一个旋转角为120︒的旋转对称图形. 如图1，点O 是等边三角形△ABC 的中心, D 、E 、F 分别为AB 、BC 、 CA 的中点, 请你将△ABC 分割并拼补成一个与△ABC 面积相等的新的旋转对称图形.FDEF DBACOABCO图1 图2小明利用旋转解决了这个问题，图2中阴影部分所示的图形即是与△ABC 面积相等的新的旋转对称图形.请你参考小明同学解决问题的方法，利用图形变换解决下列问题： 如图3，在等边△ABC 中, E 1、E 2、E 3分别为AB 、 BC 、CA 的中点，P 1、P 2, M 1、M 2, N 1、N 2分别为 AB 、BC 、CA 的三等分点.（1）在图3中画出一个和△ABC 面积相等的新的旋转 对称图形，并用阴影表示（保留画图痕迹）； （2）若△ABC 的面积为a ，则图3中△FGH 的面积为 ． （2012海淀二模） 【解析】（1）画图如下：（2）图3中△FGH 的面积为7a.图3H G F CBN 2N 1M 1M 2E 1E 2E 3P 2P 1AAPEFC DBH F GA BCE 1E 2E 3P 1P 2M 1M 2N 1N 2动手操作分为：1、立体图形及展开图；2、骰子问题；3、折纸问题；4、图形的分割；5、图形的剪拼.【例3】 ⑴如图，已知MN 是圆柱底面直径，NP 是圆柱的高.在圆柱的侧面上，过点M 、P 嵌有一圈路径最短的金属丝.现将圆柱侧面沿NP 剪开， 所得的侧面展开图是（ ）A. B. C. D. ⑵在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点，2点和5点，3点和4点)，在每一种翻动方式中，骰子不能后退．开始时骰子如图 ①那样摆放，朝上的点数是2；最后翻动到如图②所示的位置，此时骰子朝上的点 数不可能．．．是下列数中（ ）A ．5B ．4C ．3D ．1⑶ 如图，矩形纸片ABCD 中，8AB =，将纸片折叠，使顶点B 落在边AD 上的点为E ，折痕的一端G 点在边BC 上()BG GC <，另一端F 落在矩形的边上，10BG =．①请你在备用图中画出满足条件的图形；典题精练题型二：动手操作PNM P /N /PNMP /N /PNMP /N /PNMM /P /N /PNM②求出折痕GF 的长为 ．备用图（3）G 备用图（2）G DADG 备用图（1）【解析】 ⑴321n -2n ≥）. ⑵ ①正确画出图⑴、图⑵ ②545情况一：如图⑴，当点F 在AB 上时，过点G 作GH AD ⊥，则四边形ABGH 为矩形，∴8GH AB ==，10AH BG ==，设BF x =， 由图形的折叠可知BFG EFG △≌△， ∴10EG BG ==，BF EF x ==，在Rt GEH △中，由勾股定理，得6EH =，∴4AE =． ∵90A ∠=︒，8AF x =-,EF x =，222EF AF AE =+ ∴()22284x x =-+解方程，得 5x .=∴5BF =，∵10BG =，∴2255FG BG BF .=+=情况二：如图⑵,当点F 在AD 边上时，因为四边形HFGE 由四边形ABGF 折叠得到， 由折叠可知，BG EG =，AB EH =，BGF EGF ∠=∠， ∵EF BG ∥，∴BGF EFG ∠=∠，∴EGF EFG ∠=∠， ∴EF EG =，∴BG EF =,∴四边形BGEF 为平行四边形 又∵EF EG =，∴平行四边形BGEF 为菱形 连结BE ，BE 与 FG 互相垂直平分，在Rt EFH △中，10EF BG ==，8EH AB ==， 由勾股定理可得6FH AF ==，∴16AE =， ∴2285BE AE AB =+∴45BO =∴222245FG OG BG BO ==-=.【例4】 ⑴在ABC △中，沿着中位线EF 一刀剪切后，用得到的AEF △和四边形EBCF 可以拼成平行四边形EBCP ，剪切线与拼图如图所示，仿上述的方法，按要求完成下列操作设计，并画出图示．①在ABC △中，增加条件 ，沿着 H E F 图（1）G DCBA O E(B)H(A)F图（2）GDCB AA一刀剪切后可以拼成矩形；②在ABC △中，增加条件 ，沿着 一刀剪切后可以拼成菱形；③在ABC △中，增加条件 ，沿着 一刀剪切后可以拼成正方形；④在ABC △()AB AC ≠中，一刀剪切后也可以拼成等腰梯形，首先要确定剪切线，其操作过程（剪切线的作法）是： ．⑵在ABC △中，BC a =，BC 边上的高2h a =，沿图中线段DE 、CF 将ABC △剪开，分成的三块图形恰能拼成正方形CFHG ，如图⑴所示．请你解决如下问题： 在A B C '''△中，B C a ''=，B C ''边上的高12h a =．请你设计两种不同的分割方法，将A B C '''△ 沿分割线剪开后，所得的三块图形恰能拼成一个正方形，请在图⑵、图⑶中，画出分割线及拼接后的图形．【解析】 ⑴ ①方法一：90B ∠=︒，中位线EF ，如图⑴．方法二：AB AC =，中线（或高）AD ，如图⑵．②2AB BC =（或者90C ∠=︒，30A ∠=︒），中位线EF ，如图⑶． ③方法一：90B ∠=︒且2AB BC =，中位线EF ，如图⑷．方法二：AB AC =且90BAC ∠=︒，中线（或高）AD ，如图⑸．④方法一：不妨设B C ∠>∠，在BC 边上取一点D ，作GDB B ∠=∠交AB 于G ，过AC 的中点E 作EF GD ∥交BC 于F ，则EF 为剪切线．如图⑹方法二：不妨设B C ∠>∠，分别取AB 、AC 的中点D 、E ，过D 、E 作BC 的垂线，G 、H 为垂足，在HC 上截取HF GB =，连结EF ，则EF 为剪切线．如图⑺图（1）①②③H F E D B图（4）图（3）图（2）图（1）P(E)C(A)FEBAP(E)FEC(A)BAP(D)D C(A)BAP(E)FEC(A)BA图（3）图(2)A'B 'C'C'B 'A'方法三：不妨设B C ∠>∠，作高AD ，在DC 上截取DG DB =，连结AG ，过AC 的中点E 作EF AG ∥交BC 于F ，则EF 为剪切线．如图⑻图（8）图（7）图（6）图（5）P(F)A(C)ECFG D BP(F)A(C)ECFH GBD EC FGD BP(F)A(C)P(D)D C(A)BA⑵ 答案如下图：【例5】 阅读下列材料：小明遇到一个问题：如图1，正方形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 和DA 边上靠近A 、B 、C 、D 的n 等分点，连结AF 、BG 、CH 、DE ，形成四边形MNPQ ．求四边形MNPQ 与正方形ABCD 的面积比（用含n 的代数式表示）．小明的做法是：先取2n =，如图2，将ABN △绕点B 顺时针旋转90︒至CBN '△，再将ADM △绕点D 逆时针旋转90︒至CDM '△，得到5个小正方形，所以四边形MNPQ 与正方形ABCD 的面积比是15；然后取3n =，如图3，将ABN △绕点B 顺时针旋转90︒至CBN '△，再将ADM △绕点D 逆时针旋转90︒至CDM '△，得到10个小正方形，所以四边形MNPQ 与正方形ABCD 的面积比是410，即25；……请你参考小明的做法，解决下列问题：⑴在图4中探究4n =时四边形MNPQ 与正方形ABCD 的面积比（在图4上画图并直接写出结果）；⑵图5是矩形纸片剪去一个小矩形后的示意图，请你将它剪成三块后再拼成正方形（在图5中画出并指明拼接后的正方形）．(3)(2)(1)M'N'GH GH G BCEFPQM N A BCD EF PQ M NN'M'N MQ PF ED CB A ①③②图（5）A'B 'C'C'B'A'①②②①【解析】 ⑴四边形MNPQ 与正方形ABCD 的面积比是917.⑵ 如图所示：【例6】 操作探究：一动点沿着数轴向右平移5个单位，再向左平移2个单位，相当于向右平移3个单位．用实数加法表示为 5+（2-）=3．若平面直角坐标系xOy 中的点作如下平移：沿x 轴方向平移的数量为a （向右为正，向左为负，平移a 个单位），沿y 轴方向平移的数量为b （向上为正，向下为负，平移b 个单位），则把有序数对{a ，b }叫做这一平移的“平移量”．规定“平移量”{a ，b }与“平移量”{c ，d }的加法运算法则为}{}{}{d b c a d c b a ++=+，，，． （1）计算：{3，1}+{1，2}；（2）若一动点从点A （1，1）出发，先按照“平移量”{2，1}平移到点B ，再按照“平移量”{-1，2}平移到点C ；最后按照“平移量”{-2，-1}平移到点D ，在图中画出四边形ABCD ，并直接写出点D 的坐标；（3）将（2）中的四边形ABCD 以点A 为中心，顺时针旋转90°，点B 旋转到点E ，连结典题精练H G M'N'A BC DEF PQMN DCB（5）(4)H GAB C D EF P Q MN题型三：新定义AE、BE若动点P从点A出发，沿△AEB的三边AE、EB、BA平移一周．请用“平移量”加法算式表示动点P的平移过程．（2013丰台二模）【解析】（1）{4，3}．（2）①画图②D(0，3).（3）{1，-2}+{1，3}+{-2，-1}．yxO 11yxBACDO 11【例7】 如图1，四边形ABCD 中，AC 、BD 为它的对角线，E 为AB 边上一动点（点E 不与点A 、B 重合），EF ∥AC 交BC 于点F ，FG ∥BD 交DC 于点G ，GH ∥AC 交AD 于点H ，连接HE ．记四边形EFGH 的周长为p ，如果在点E 的运动过程中，p 的值不变，则我们称四边形ABCD 为“Ω四边形”， 此时p 的值称为它的“Ω值”．经过探究，可得矩形是“Ω四边形”．如图2，矩形ABCD 中，若AB =4，BC =3，则它的“Ω值”为 ．图1B FCGD HE A图2D CBA图3ODBA（1）等腰梯形 （填“是”或 “不是”）“Ω四边形”；（2）如图3，BD 是⊙O 的直径，A 是⊙O 上一点，=34AD AB =，，点C 为»AB 上的一动点，将△DAB 沿CD 的中垂线翻折，得到△CEF ．当点C 运动到某一位置时，以A 、B 、C 、D 、E 、F 中的任意四个点为顶点的“Ω四边形”最多，最多有 个．（2013海淀二模）【解析】 “Ω值”为10．（1）是；（2）最多有5个．训练1. ⑴将如右图所示的圆心角为90︒的扇形纸片AOB 围成圆锥形纸帽，使扇形的两条半径OA 与OB 重合(接缝粘贴部分忽略不计)，则围成的圆锥形纸帽是（ ）⑵如图是一个等腰直角三角形纸片，按图中裁剪线将这个纸片裁剪成三部分．请你将这三部分小纸片重新分别拼接成：(1)一个非矩形的平行四边形； (2)一个等腰梯形；(3)一个正方形．请画出拼接后的三个图形．【解析】 ⑴B. ⑵训练2. 图⑴、图⑵均为76⨯的正方形网格，点A 、B 、C 在格点上.⑴在图⑴中确定格点D ，并画出以A 、B 、C 、D 为顶点的四边形，使其为轴对称图形.（画一个即可）⑵在图⑵中确定格点E ，并画出以A 、B 、C 、E 为顶点的四边形，使其为中心对称图形.（画一个即可）（吉林长春）【解析】 ⑴ 有以下答案供参考：思维拓展训练(选讲)图（2）图（1）ABCCBADD A BCCBA⑵ 有以下答案供参考：EEABCCBA训练3. ⑴图⑴是一个八角星形纸板，图中有八个直角，八个相等的钝角,每条边都相等.如图⑵将纸板沿虚线进行切割，无缝隙无重叠的拼成图⑶所示的大正方形,其面积为842+则图⑶中线段AB 的长为 .（海淀二模）图（3）图（2）图（1）BA⑵如图⑶，在55⨯的网格中有一个正方形，把正方形的各边三等分，分别以居中那条线段为斜边向外作等腰直角三角形，去掉居中的那条线段，得到图⑷，请把图⑷中的图形剪拼成正方形，并在图⑷中画出剪裁线，在图⑸中画出剪拼后的正方形．（石景山一模）图（5）图（4）图（3）【解析】215.⑵如图所示：【练习1】 已知ABC △，63ABC ACB ∠=∠=°．如图1所示，取三边中点，可以把ABC △分割成四个等腰三角形．请你在图2中，用另外四种不同的方法把ABC △分割成四个等腰三角形，并标明分割后的四个等腰三角形的底角．．的度数（如果经过变换后两个图形重合，则视为同一种方法）.（海淀二模）【解析】 分割为等腰三角形常用方法:①角分线+平行线.如图⑴和图⑵ ②直角三角形+斜边中线.如图⑶(和图⑴)③顶角为特殊角度108︒的等腰三角形可以无限分割成36︒和72︒为底角的等腰三角形.如图⑷④知一等腰三角形，做此三角形的对称轴，然后再去分割.如图⑸复习巩固图1CBACB AAB C C B AAB C 图254°54°72°54°36°36°36°31.5°31.5°31.5°27°27°27°27°27°27°27°27°27°63°63°63°63°63°63°63°63°63°63°63°63°63°63°63°36°72°54°27°31.5°63°(5)(4)(3)(2)(1)【练习2】 现场学习题问题背景：在ABC △中，AB 、BC 、AC 21317三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格(每个小正方形的边长为1)，再在网格中画出格点ABC △（即ABC △三个顶点都在小正方形的顶点处），如图⑴所示．这样不需求ABC △的高，而借用网格就能计算出它的面积． ⑴请你将ABC △的面积直接填写在横线上．________ 思维拓展：⑵我们把上述求ABC △面积的方法叫做构图法．若ABC △2a 、25a 26a (0)a >，请利用图⑵的正方形网格(每个小正方形的边长为a )画出相应的ABC △，并求出它的面积是： ． 探索创新：⑶若ABC △三边的长分别为224m n +、2216m n +、222m n +(0,0,)m n m n >>≠ ，请运用构图法在图⑶指定区域内画出示意图，并求出ABC △的面积为： ．【解析】 ⑴25． ⑵ 面积：23a ．⑶ 面积：3mn ．图（2）A B C 4m 2m 2m n n 2n C B A 图（3）图（3）图（2）图（1）A B C【练习3】 在如图1中，正方形ABCD 的边长为a ，等腰直角三角形FAE的斜边2AE b =，且边AD 和AE 在同一直线上． 操作示例：当2b a <时，如图1，在BA 上选取点G ，使BG b =，连结FG 和CG ，裁掉FAG △和CGB △并分别拼接到FEH △和CHD △的位置构成四边形FGCH ．思考发现：小明在操作后发现：该剪拼方法就是先将FAG △绕点F 逆时针旋转90︒到FEH △的位置，易知EH 与AD 在同一直线上．连结CH ，由剪拼方法可得DH BG =，故CHD CBG △≌△，从而又可将CGB △绕点C 顺时针旋转90︒到CHD △的位置．这样，对于剪拼得到的四边形FGCH （如图1），过点F 作FM AE ⊥于点M （图略），利用SAS 公理可判断HFM CHD △≌△，易得FH HC GC FG ===，90FHC ∠=︒．进而根据正方形的判定方法，可以判断出四边形FGCH 是正方形．实践探究：⑴ 正方形FGCH 的面积是__________；（用含a ，b 的式子表示）⑵ 类比图1的剪拼方法，请你就如图2至如图4的三种情形分别画出剪拼成一个新正方形的示意图．联想拓展：小明通过探究后发现：当b a ≤时，此类图形都能剪拼成正方形，且所选取的点G 的位置在BA 方向上随着b 的增大不断上移．⑶ 当b a >时，如图5的图形能否剪拼成一个正方形？若能，请你在图中画出剪拼的示意图；若不能，简要说明理由．【分析】 抓22a b +，结合四边形ABCD 为正方形及给出的图１中的作法，只需满足BG DH =，由全等三角形即可得出CG 和CH 互相垂直平分且相等．再按照提示方法可以证明四边形GCHF 为正方形．【解析】 ⑴ 22a b +； ⑵ 剪拼方法如图2至图4．⑶ 能；剪拼方法如图5（图中BG DH b ==）．先沿FH 剪一刀，将FEH △拼接到图1(2b <a )H G FE DCB A 图２FA B C(E ) DH G F 图４ABC DF图３A BCEHD G C F图５ABDG H a<2b=a FEDC B A图3FD(E )C BA 图2a<2b<2a FEDCBA图3b>b=a 图4ABC DEF图5FEDCB A b>a 图5FE D C BA△即可．FAG△拼接到HDC△；再沿GC剪一刀，将GBC第十八种品格：坚持坚持即是成功有一个少年，拜在一位师傅门下，想学功夫。

1第五级（下）·第1讲·提高-尖子班·教师版MABCD EF GH O题型一 垂径定理 巩固练习【练习1】 【解析】 B ． 【练习2】 【解析】 ⑴ ∵AB OC ∥，∴BAC C ∠=∠， ∵O A O C =，∴O AC C ∠=∠，∴BAC O AC ∠=∠，∴A C 平分O AB ∠． ⑵ ∵O E A B ⊥，∴112AE AB ==，在R t AO E △中，9030OEA AOE ∠=︒∠=︒，，∴223AO AE OE ===， 以下可以用两种不同方法解答： 解法一：∵AB OC ∥，∴12AE PE O CO P==∴1333PE O E ==．解法二：由⑴得A C 平分O AB ∠， 由角平分线定理可得2O A O P AEPE==，∴1333PE O E ==．【练习3】 【解析】 过O 点作O M EF ⊥于M 点，∴M 是EF 中点，∵GE EF HF EF ⊥⊥，，∴GE HF ∥，又O M EF ⊥，∴GE OM HF ∥∥， ∴O 是C D 中点，∵O A O B =，∴AC BD =．复习巩固1圆中三大基本定理2第五级（下）·第1讲·提高-尖子班·教师版题型二 弧、弦、圆心角、弦心距的关系定理 巩固练习 【练习4】【解析】 ⑴ ∵A C B F =，∴ AC BF=， ∵AB 是直径，∴ AEB ADB =，∴ AEB AC ADB BF -=-，即 BEC ADF =． ⑵ 由⑴可知C AM FBN ∠=∠，∵CD EF ∥，∴C M A D M B FN B ∠=∠=∠，又A C B F =，∴AC M BFN △≌△，∴AM BN =．题型三 圆周角定理 巩固练习【练习5】 【解析】 ⑴①√；②×；③√．⑵ 20︒．⑶ 60︒，2cm ．⑷ B ．方法要求：⑴ 知道直径所对的圆周角为90︒．⑵ 在同圆或等圆中，同弧所对的圆周角相等．【练习6】 【解析】 ⑴1；⑵40︒. 【练习7】 【解析】 ⑴ 22.567.5︒︒，；⑵ ∵圆周被6等分，∴ 111223360660B C C C C C ===÷=︒． ∵直径11AD B C ⊥，∴1111302AC B C ==︒， ∴()()12311153060453060607522B B B ∠=︒∠=⨯︒+︒=︒∠=⨯︒+︒+︒=︒，，．⑶ ()()90451136036012222n n B n n n n -︒︒︒⎡⎤∠=⨯+-⋅=⎢⎥⎣⎦（或3604590908n B n n ︒︒∠=︒-=︒-）【练习8】【解析】 解法一：补短法过B 点作BN C D ⊥交D C 延长线于N ．∵BM AC BN CD ⊥⊥，，∴90AM B D N B ∠=∠=︒， ∵AB DB BAM BDN =∠=∠，，∴ABM D BN △≌△， ∴AM DN BM BN ==，∵BC N BAD BD A BC M ∠=∠=∠=∠，∴BC M BC N △≌△，∴C M C N =，∴AM D N D C C N D C C M ==+=+．（或延长D C 到N ，使D N AM =，连结B N ，也可证得结论．）解法二：截长法在AM 上取一点P ，使得AP D C =，连结BP ． 则很容易证明ABP D BC △≌△，∴BP BC =， ∵BM AC ⊥，∴P M C M =，3 第五级（下）·第1讲·提高-尖子班·教师版∴AM AP PM D C C M =+=+．古往今来，古今中外，很多人取得了各种成就。

“圆”来如此漫画释义满分晋级7圆的概念及性质圆1级 圆的 概念及性质圆2级 与圆有关 的位置关系 圆3级 正多边形和圆 与圆中的计算暑期班 第七讲暑期班 第八讲暑期班 第九讲中考内容中考要求A B C圆的有关概念理解圆及其有关概念会过不在同一直线上的三点作圆；能利用圆的有关概念解决简单问题圆的性质知道圆的对称性，了解弧、弦、圆心角的关系能用弧、弦、圆心角的关系解决简单问题能运用圆的性质解决有关问题圆周角了解圆周角与圆心角的关系；知道直径所对的圆周角是直角会求圆周角的度数，能用圆周角的知识解决与角有关的简单问题能综合运用几何知识解决与圆周角有关的问题垂径定理会在相应的图形中确定垂径定理的条件和结论能用垂径定理解决有关问题点与圆的位置关系了解点与圆的位置关系直线与圆的位置关系了解直线与圆的位置关系；了解切线的概念，理解切线与过切点的半径之间的关系；会过圆上一点画圆的切线；了解切线长的概念能判定直线和圆的位置关系；会根据切线长的知识解决简单的问题；能利用直线和圆的位置关系解决简单问题能解决与切线有关的问题圆与圆的位置关系了解圆与圆的位置关系能利用圆与圆的位置关系解决简单问题弧长会计算弧长能利用弧长解决有关问题中考内容与要求扇形会计算扇形面积能利用扇形面积解决有关问题圆锥的侧面积和全面积会求圆锥的侧面积和全面积能解决与圆锥有关的简单实际问题圆是北京中考的必考内容，主要考查圆的有关性质与圆的有关计算，每年的第20题都会考查，第1小题一般是切线的证明，第2小题运用圆与三角形相似、解直角三角形等知识求线段长度问题，有时也以阅读理解、条件开放、结论开放探索题作为新的题型。

要求同学们重点掌握圆的有关性质，掌握求线段、角的方法，理解概念之间的相互联系和知识之间的相互转化，理解直线和圆的三种位置关系，掌握切线的性质和判定方法，会根据条件解决圆中的动态问题。

年份2010年2011年2012年题号11，20 20，25 8，20，25分值9分13分17分考点垂径定理的应用；切线判定、圆与解直角三角形综合圆的有关证明，计算（圆周角定理、切线、等腰三角形、相似、解直角三角形）；直线与圆的位置关系圆的基本性质，圆的切线证明，圆同相似和三角函数的结合；直线与圆的位置关系中考考点分析定 义示例剖析圆：在一个平面内，线段OA 绕它固定的一个端点O 旋转一周，另一个端点A 所形成的图形叫做圆． 固定的端点O 叫做圆心，线段OA 叫做半径． 由圆的定义可知：⑴ 圆上的各点到圆心的距离都等于半径长；在一个平面内，到圆心的距离等于半径长的点都在同一个圆上．因此，圆是在一个平面内，所有到一个定点的距离等于定长的点组成的图形． ⑵ 要确定一个圆，需要两个基本条件，一个是圆心的位置，另一个是半径的长短，其中，圆心确定圆的位置，半径长确定圆的大小． 圆O半径圆心AO表示为“O ⊙”圆心相同且半径相等的圆叫做同圆；圆心相同，半径不相等的两个圆叫做同心圆； 能够重合的两个圆叫做等圆．等圆O‘O同心圆O知识互联网模块一 圆的基本概念知识导航OEDCB A 弦和弧：1. 连结圆上任意两点的线段叫做弦．经过圆心的弦叫做直径，并且直径是同一圆中最长的弦，直径等于半径的2倍．2. 圆上任意两点间的部分叫做圆弧，简称弧． 以A B 、为端点的弧记作»AB ，读作弧AB ． 在同圆或等圆中，能够互相重合的弧叫做等弧． 3. 圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．4. 在一个圆中大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧．Cm劣弧优弧弦BAO表示：劣弧»AB优弧¼ACB 或¼AmB 圆心角和圆周角：1. 顶点在圆心的角叫做圆心角．2. 顶点在圆上，并且两边都和圆相交的角叫做圆周角．O DC BA 圆周角圆心角下面这些都不是圆周角：【例1】 如图，若点O 为O ⊙的圆心，则线段_________________是圆O 的半径；线段___________是圆O 的弦，其中最长的弦是________；________是劣弧；___________是半圆．若40A ∠=︒，则ABO ∠=_________，C ∠=_______，ABC ∠=_______．【例2】 如图，AB 为O ⊙的直径，CD 是O ⊙的弦，AB CD 、的延长线交于点E ，若2AB DE =，18E ∠=︒，求AOC ∠的度数．能力提升夯实基础OCBAD CBA NM O定 理示例剖析1. 垂直于弦的直径平分弦，并且平分弦所对的两条弧．2. 平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧.如图，AB 是O ⊙的直径，CD 是弦E DCBAO1. 若AB CD ⊥于E ，则CE DE =； »»AC AD =；»»BC BD =．2. 若CE DE =，则AB CD ⊥； »»AC AD =；»»BCBD =．【例3】 1．如图，M N 、分别是O ⊙中长度相等但不平行的两条弦AB CD 、的中点．求证：AMN CNM ∠=∠．2．如图，∠P AC =30°，在射线AC 上顺次截取AD =3cm ，DB =10cm ，以DB 为直径作⊙O 交射线AP 于E 、F 两点，则线段EF 的长是 cm ．知识导航模块二 垂直于弦的直径FE ADOB CP3．如图，⊙O 的半径为2，弦32=AB ，点C 在弦AB 上，AB AC 41=，则OC 的长为（ ）A ．2 B ．3 C ．23 D ． 7【例4】 ⊙O 的半径为5cm ，弦AB ∥CD ，且AB =8 cm ，CD =6cm ，求AB 与C 之间的距离．定 理示例剖析弧、弦、圆心角之间的关系：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量分别相等． O D CB A如图，由定理可知：若AOB COD ∠=∠，则AB CD =、»»AB CD =；若AB CD =，则AOB COD ∠=∠、»»AB CD =； 若»»AB CD =，则AB CD =、AOB COD ∠=∠．能力提升知识导航BCAO圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论1：在同圆或等圆中，如果两个圆周角相等，它们所对的弧一定相等． 推论2：半圆（或直径）所对的圆周角是直角，90︒的圆周角所对的弦是直径．C BAO2AOB ACB ∠=∠EO DCB A若ACB AED ∠=∠，则»»AB AD =直角直径OCB A圆内接多边形：如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆.圆内接四边形的对角互补．如图，A B C D 、、、四点都在圆上，OD CBA则180A C ∠+∠=︒，180B D ∠+∠=︒、【例5】 ⑴ 已知，A B C 、、分别为O ⊙圆周上任意三点，请你判断同弧所对的ACB ∠与AOB∠的大小关系．O OO根据上面的推理，可以发现：__________________________________________________．⑵ 若点D 是优弧»AB 上任意一点，试判断ADB ∠与ACB ∠的大小关系． 根据上面的推理，可以发现：__________________________________________________．⑶ 如果点D 在劣弧»AB 上，此时ADB ∠和ACB ∠的大小关系还一样吗？可夯实基础ODCA以得到什么结论？COADE O B DFCA【例6】 ⑴ 如图，△ACD 和△ABE 都内接于同一个圆，则∠ADC +∠AEB +∠BAC =⑵ 在⊙O 中，直径AB ⊥CD 于点E ，连接CO 并延长交AD 于点F ， 且CF ⊥AD ．则∠D = ．⑶ 如图，点A 、B 、C 、D 在⊙O 上，O 点在∠D 的内部，四边形OABC 为平行四边形，则∠OAD +∠OCD = °．⑷ 如图，A B C D 、、、是O ⊙上的点，直径AB 交CD 于点E ，已知 57C ∠=︒，45D ∠=︒，则CEB ∠=________．⑸ 已知O ⊙的弦AB 长等于圆的半径，则该弦所对的圆周角为 ．【例7】 已知：在半径为52的⊙O 内，有互相垂直的两条弦AB ，CD ，它们相交于P 点．（1）求证：P A ·PB =PC ·PD ；（2）设BC 的中点为F ，连接FP 并延长交AD 于E ，求证：EF ⊥AD ； （3）如果AB =8，CD =6，求O 、P 两点之间的距离．判断正误能力提升探索创新EDCBA OCBADCB ED APEDOBFCAOGFE DC BAOEDCBA⑴ 半圆是弧⑵ 半径相等的两个圆是等圆⑶ 过圆心的线段是直径⑷ 两个端点能够重合的弧是等弧⑸ 圆的任意一条弦把圆分成优弧和劣弧两部分 ⑹ 长度相等的弧是等弧 ⑺ 直径是最大的弦 ⑻ 半圆所对的弦是直径 ⑼ 两个劣弧的和是半圆⑽ 圆的半径是R ，则弦长的取值范围是大于0且不大于2R.训练1. 如图，CD 是O ⊙的直径，87EOD ∠=︒，AE 交O ⊙于B ，且AB OC =，求A ∠的度数．训练2. 图，矩形ABCD 与圆心在AB 上的O ⊙交于点G B F E 、、、，8cm GB =，1cm AG =，2cm DE =，则EF =_________．训练3. ⑴ 如图，O ⊙的直径为10，弦8AB =，P 是线段AB 上一点，则OP 的取值范围是________________．思维拓展训练(选讲)OBA⑵ 如图，将O ⊙沿着弦AB 翻折，劣弧恰好经过圆心O ，若O ⊙的半径为6，则弦AB 的长度等于_________．训练4. 如图，O ⊙中，AB 为直径，弦CD 交AB 于P ，且OP PC ，试猜想»AD 与»BC之间的关系，并证明你的猜想．OPABPCOAO DC BA E知识模块一 圆的基本概念 课后演练【演练1】 已知：如图，在同心圆中，大圆的弦AB 交小圆于C D ，两点．⑴ 求证：AOC BOD ∠=∠；⑵ 试确定AC 与BD 两线段之间的大小关系，并证明你的结论．知识模块二 垂直于弦的直径 课后演练【演练2】 如图所示，在Rt ABC △中，90C ∠=︒，2AC =，1BC =，若以C 为圆心、CB 的长为半径的圆交AB 于P ，则AP = .【演练3】 如图所示，已知AB 为O ⊙的直径，CD 是弦，且AB CD ⊥于点E ，连接AC OC BC 、、， ⑴ 求证：ACO BCD ∠=∠，⑵ 若8cm 24cm EB CD ==，，求O ⊙的直径．知识模块三 弧、弦、圆心角和圆周角 课后演练实战演练DCAOPABC【演练4】 已知如图，在O ⊙中，AB 是O ⊙的直径，AC 、BC 分别交O ⊙于E 、D ，D 是»BE的中点，40A ∠=︒，求C ∠的大小．【演练5】 如图，ABC △内接于O ⊙，OD AC ⊥于D ，2OD =，4OC =，则B ∠=________．OD CB A OE DCBA第十七种品格：成就史蒂芬与他的导演梦史蒂芬·史匹柏在36岁时就成为世界上最成功的制片人，电影史上十大卖座的影片中，他个人囊括四部。

冒险记！！漫画释义满分晋级6锐角三角函数三角形13级 相似三角形 的简单模型三角形14级 锐角三角函数三角形15级 垂直模型中 的相似及变形暑期班 第五讲暑期班 第六讲秋季班 第七讲中考内容中考要求A B C锐角三角函数了解锐角三角函数（sin A，cos A，tan A）；知道30°，45°，60°角的三角函数值由某个锐角的一个三角函数值，会求这个角的其余两个三角函数值；会计算含有30°，45°，60°角的三角函数式的值能运用三角函数解决与直角三角形有关的简单问题解直角三角形的知识是近年各地中考的热点之一，考查内容以基础知识与基本技能为主。

应用意识进一步增强，联系实际，综合运用知识、技能的要求也越来越高。

北京中考题中的第13题是简单的三角函数计算，第20题是计算长度问题，一般可以转化为直角三角形运用三角函数得到解决。

本部分内容要求同学们能掌握三角函数的概念，会熟练运用特殊角的三角函数值；将实际问题转化为数学问题，建立数学模型；涉及解斜三角形的问题时，构造数学几何模型，即通过添加适当的辅助线将解一般三角形转化为解直角三角形。

年份2010年2011年2012年题号13，25 13，20 13，20分值12分11分10分考点三角函数计算；运用三角函数解直角三角形三角函数计算；运用三角函数解直角三角形三角函数计算；运用三角函数解直角三角形中考考点分析中考内容与要求知识互联网定 义示例剖析锐角三角函数定义：在Rt ABC △中，90C ∠=︒，A ∠、B ∠、C ∠所对三角形的边分别为a 、b 、c ．正弦：sin a A c =； 余弦：cos bA c =；正切：tan a A b =； 若12AC =，5BC =，13AB =则5sin 13BC A AB ==12cos 13AC A AB ==5tan 12BC A AC ==特殊角的三 角函数值：三角函数 角度sin αcos α tan α30︒ 12 32 3345︒ 22 22 160︒32123锐角三角函数的性质： 1. 同角三角函数关系： 22sin cos 1A A +=，sin tan cos AA A=. 2. 互为余角三角函数关系：1．22sin 30cos 301+=°°，sin 25tan 25cos25°°=°.2．sin70cos20=°°模块一 锐角三角函数定义与计算知识导航C B A C BA⑴ 任意锐角的正弦值等于它的余角的余弦值：()sin cos 90A A =︒-；⑵ 任意锐角的余弦值等于它的余角的正弦值：()cos sin 90A A =︒-；cos10sin80=°°锐角三角函数值的变化规律： 当角度在0~90︒︒范围内变化时， 正弦值随角度增大（或减小）而增大（或减小）； 余弦值随角度增大（或减小）而减小（或增大）． 正切值随角度增大（或减小）而增大（或减小）；比较角的正弦、余弦、正切值的大小，其规律是： A B ，为锐角且A B >，则sin sin A B >，cos cos A B <，tan tan A B >．该规律反过来也成立．【例1】 ⑴ 如图，在Rt ABC △中，=90C ︒∠，三边分别为a 、b 、c ，则cos A 等于（ ）A ．a cB ．a bC ．b aD ．bc⑵ 在Rt ABC △中，90C =︒∠，A ∠、B ∠、C ∠所对三角形的边分别为a 、b 、c ． 若3a =，4b =，则c = ，sin A = ，cos A = ，tan A = ，sin B = ，cos B = ， tan B = ⑶ 在Rt △ ABC 中，∠C =900，若AB =2AC ，则sinA 的值是（ ）A .3B .12C.3D.3⑷ 计算：011122cos30(31)()8--︒+--【例2】 ⑴已知3tan 3α=，则锐角α的度数是 ︒．⑵如图，在Rt △ABC 中，∠C ＝90°，AM 是BC 边上的中线， 若cos ∠CAM =45，则tan ∠B 的值为 ．能力提升夯实基础cba CBA ACMB⑶若()6cos 1633α-︒=，则锐角α的角度是 .⑷正方形网格中，AOB ∠如图放置，则AOB ∠tan 的值为（ ） A ．55 B ．255 C ．12 D ．2⑸如图，A 、B 两点在河的两岸，要测量这两点之间的距离，测量 者在与A 同侧的河岸边选定一点C ，测出AC =a 米，∠A =90°， ∠C =40°，则AB 等于（ ）米． A ．a sin40° B ．a cos40° C ．a tan40° D ．︒40tan a1．解直角三角形的概念在直角三角形中，除直角外，一共有5个元素，即3条边和2个锐角，由直角三角形中除直角外的已知元素，求出所有未知元素的过程，叫做解直角三角形． 2．直角三角形的边角关系 ⑴ 三边之间的关系：222a b c +=．（勾股定理）⑵ 锐角之间的关系：90A B ∠+∠=︒ ⑶ 边角之间的关系：sin cos tan a b aA A A c c b===，，．3. 解直角三角形的四种基本类型已知条件解法类型一条边和一个锐角 斜边c 和锐角A ∠ 90B A ∠=︒-∠，sin a c A =，cos b c A =直角边a 和锐角A ∠90B A ∠=︒-∠，tan a b A=，sin ac A = 两条边两条直角边a 和b 22c a b =+，由tan a A b=，求A ∠，90B A ∠=︒-∠ 斜边c 和直角边a22b c a =-，由sin aA c=，求A ∠，90B A ∠=︒-∠ 4．基本图形知识导航模块二 解直角三角形cba CBA CBAABO30︒45︒30︒45︒平移60︒45︒重叠型翻折平移45︒30︒45︒30︒两侧型45︒60︒【例3】 ⑴ 在Rt ABC △中，90C =︒∠，10AB =，8BC =，求A sin 和B tan 的值．⑵如图，在Rt △ABC 中，∠C =90°，点D 在AC 边上．若 DB =6，AD =12CD ，sin ∠CBD =23，求AD 的长和tan A 的值．夯实基础BAD C⑶ 如图，在Rt ABC △中，90ACB =︒∠，CD AB ⊥于点D ．已知5AC =，5sin ACD =∠，① 求AD 的长；② 求AB 的长．实际应用中的概念⑴ 仰角与俯角：在视线与水平线所成的角中，视线在水平线上方的叫做仰角，在水平线下方的叫做俯角．如图⑴．⑵ 坡角与坡度：坡面的垂直高度h 和水平宽度l 的比叫做坡度（或叫做坡比），用字母表示为h i l=，坡面与水平面的夹角记作α，叫做坡角，则tan hi l α==．坡度越大，坡面就越陡．如图⑵．⑶ 方向角（或方位角）：方向角一般是指以观测者的位置为中心，将正北或正南方向作为起始方向旋转到目标的方向线所成的角（一般指锐角），通常表达为北（南）偏东（西）××度．如图⑶．γβα图(3)北i =h :l图(2)αl h图(1)俯角仰角视线视线水平线铅垂线知识导航模块三 锐角三角函数的应用D C A【例4】如图，某校数学兴趣小组的同学在测量建筑物AB的高度时，在地面的C处测得点A的仰角为45°，向前走50米到达D处，在D处测得点A的仰角为60°，求建筑物AB的高度．【例5】如图，某船向正东方向航行，在A处望见小岛C在北偏东60°方向，前进8海里到达B 点，测得小岛C在北偏东30°方向．已知该岛5海里内有暗礁，若该船继续向东航行，有无触礁危险？请通过计算说明理由．（参考数据：3 1.732）北东C东北CDBA夯实基础能力提升ADB45°60°【例6】 如图是黄金海岸的沙丘滑沙场景.已知滑沙斜坡AC 的坡度是43tan =α，在与滑沙坡底C 距离20米的D 处，测得坡顶A 的仰角为26.6°，且点D 、C 、B 在同一直线上，求滑坡的高AB （结果取整数：参考数据：sin26.6°=0.45，cos26.6°=0.89，tan26.6°=0.50）．第20题图ABDC20米26.6°α【例7】 小强在江的南岸选定建筑物A ，并在江北的B 处观察，此时，视线与江岸BE 所成的夹角是30︒，小强沿江岸BE 向东走了500米，到C 处，再观察A ，此时视线AC 与江岸所成的夹角60︒，根据小强提供的信息，你能测出江宽吗？若能，写出求解过程，（结果保留根号）；若不能，请说明理由．判断对错⑴ tan22tan αα=（ ）⑵ ()cos cos cos A B A B +=+（ ）_____________________⑴ 若锐角α、β满足αβ=，3sin 5α=，则cos β= ． ⑵ 已知：A ∠是锐角且满足5sin 13A =，则()sin 90A -=° _____________________比较sin57°和cos57°的大小．_____________________探索创新训练1. 计算：⑴ 22sin 60tan 45cos30tan30︒⋅︒+︒⋅︒ ⑵()23cos605sin30tan36sin 55︒︒-︒-︒⑶ 2sin 452cos60tan 453tan 60++-°°°°⑷ cos453tan30cos302sin602tan45︒+︒+︒+︒-︒⑸ 22211cos 45cos 30sin 45sin30tan30︒-++︒+︒︒︒训练2. 化简：2sin 402sin 401sin 40sin50cos40sin 40︒+︒++︒-︒-︒-︒；训练3. 如图，90D ∠=°，10BC =，30CBD ∠=°，15A ∠=°．⑴ 求CD 的长；⑵ 求tan A 的值．DCB A训练4. 超速行驶是引发交通事故的主要原因，上周末，小明等三位同学在阜石路杨庄路段，尝试用自己所学的知识检测车速，观察点设在到公路l 的距离为100米的P 处．这时，一思维拓展训练(选讲)辆富康轿车由西向东匀速驶来，测得此车从A处行驶到B处所用的时间为4秒，并测得60APO∠=︒，45BPO∠=︒，试判断此车是否超过了每小时60千米的限制速度？（参考数据：2 1.41=，3 1.73=）知识模块一锐角三角函数定义与计算【演练1】在ABC△中，若23tan1cos0A B⎛⎫-+-=⎪⎪⎝⎭，则A B∠+∠=．【演练2】⑴计算：sin30cos45sin45tan60+⋅-°°°°⑵计算：11sin60tan30(cos452)3-⎛⎫+---⎪⎝⎭°°°知识模块二解直角三角形【演练3】已知如图，Rt ABD△中，90D=︒∠，45B=︒∠，60ACD=︒∠，10BC=，求AD的长．实战演练ABCD知识模块三锐角三角函数的应用【演练4】如图，小明在十月一日到公园放风筝，风筝飞到C处时的线长为20米，此时小明正好站在A处，并测得60∠=°，CBD牵引底端B离地面1.5米，求此时风筝离地面的高度．（结果保留根号）【演练5】如图，甲船在港口P的南偏西60︒方向，距港口86海里的A处，沿AP方向以每小时15海里的速度匀速驶向港口P．乙船从港口P出发，沿南偏东45︒方向匀速驶离港口P，现两船同时出发，2小时后乙船在甲船的正东方向．求乙船的航行速度．（结果精确到个位，参考数据：2 1.414≈）≈，3 1.732北P东A第十七种品格：成就毛毛虫与跟风美国一个研究“成功”的机构，曾经长期追踪一百个年轻人，直到他们年满六十五岁。

此文档下载后即可编辑初三数学：二次函数考点分析二次函数的图像考点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点．二次函数：y=ax 2+bx+c （a ，b ，c 是常数，a ≠0）一般式：y=ax 2+bx+c ，三个点顶点式：y=a （x －h ）2+k ，顶点坐标对称轴顶点坐标（－2b a ，244ac b a -）． 顶点坐标（h ，k ）a b c 作用分析│a │的大小决定了开口的宽窄，│a │越大，开口越小，│a │越小，开口越大，a ，b 的符号共同决定了对称轴的位置，当b=0时，对称轴x=0，即对称轴为y 轴，当a ，b 同号时，对称轴x=－2b a <0，即对称轴在y 轴左侧，当a ，b•异号时，对称轴x=－2b a>0，即对称轴在y 轴右侧，c•的符号决定了抛物线与y 轴交点的位置，c=0时，抛物线经过原点，c>0时，与y 轴交于正半轴；c<0时，与y•轴交于负半轴，以上a ，b ，c 的符号与图像的位置是共同作用的，也可以互相推出．交点式：y=a(x- x 1)(x- x 2)，（有交点的情况）与x 轴的两个交点坐标x 1，x 2对称轴为221x x h +=一、二次函数解析式及定义型问题(顶点式中考要点)１.把二次函数的图象向左平移2个单位，再向上平移1个单位，所得到的图象对应的二次函数关系式是2)1(2-+=x y 则原二次函数的解析式为２.二次函数的图象顶点坐标为（2，1），形状开品与抛物线y= - 2x 2相同，这个函数解析式为________。

３.如果函数1)3(232++-=+-kx x k y k k 是二次函数,则k 的值是______４.已知点11()x y ，，22()x y ，均在抛物线21y x =-上，下列说法中正确的是（ ）A ．若12y y =，则12x x =B ．若12x x =-，则12y y =-C ．若120x x <<，则12y y >D ．若120x x <<，则12y y >５.抛物线c bx x y ++=2图像向右平移2个单位再向下平移3个单位，所得图像的解析式为322--=x x y ，则b 、c 的值为A . b=2， c=2 B. b=2，c=0C . b= -2，c=-1 D. b= -3， c=2６.抛物线5)43()1(22+--++=x m m x m y 以Y 轴为对称轴则。

第一讲一次函数和反比例函数 知识点、重点、难点 函数y 二kx=0）称为一次函数，其函数图像是一条直线。

若b =0时，则称函数y = kx 为正比例函数，故正比例函数是一次函数的特殊情况。

当k • 0时，函数y = kx • b 是单调递增函数，即函数值 y 随X 增大（减小）而增大（减小）；当 k ::： 0， y =kx b 是递减函数，即函数值 y 随x 增大（减小）而减小（增大）。

ky （k=0） 函数 x 称为反比例函数，其函数图像是双曲线。

当k 0且x 0时，函数值y 随X 增大（减小）而减小（增大）；当 k 0且x ：：：0，函数值y 随X 增大ky =—（减小）而减小（增大），也就是说：当 k 0时，反比例函数x 分别在第一或第三象限内是单调递ky =—减函数；当k ：：：0时，函数 x 分别在第二或第四象限内是单调递增函数。

y = k 1x b i K = 0）, y = k 2x b 2（k 2= 0）.若当« = k 2时，0 = b 2时，两面直线平行。

当« =k 2时，b i =b 2时，两面直线重合。

当k i ^k 2时，两直线相交。

当二-1时，两直线互相垂直。

求一次函数、反比例函数解析式，关键是要待定解析式中的未知数的系数；其次，在解题过程中要重 视数形相结合。

例题精讲例1 ：在直角坐标平面上有点A（-1, -2）、B （4, 2）、C （1，c ），求c 为何值时AC - BC 取最小值。

解显然，当点C 在线段AB 内时，AC BC 最短。

设直线AB 方程为= kx b，代入A —2）、B （4, 2）2k -1 k -10y = -------- x -- -------例2 :求证：一次函数k 2 k 2的图像对一切有意义的 k 恒过一定点，并求这个定点。

-k b = -2得4k • b = 2,解得所以线段AB 为4 6y x (T 5 5 沁空4）,代入 C（1，c ），c 1 -6解由一次函数得（k py =（2k-1）x-（k-10）,整理得（2x-y-1）k-x-2y Fn。

1.如图，AB是⊙O的直径，弦CD交AB于点E，且AE＝CD＝8，则⊙O的半径为_______。

2.如图，AB是⊙O的直径，点E是BD上一点，∠DAC＝∠AED。

⑴求证：AC是⊙O的切线；⑵若点E是BD的中点，连结AE交BC于点F，当BD＝5，CD＝4时，求DF的值。

3.如图，AB是⊙O的直径，点C在⊙O上，CE⊥AB于E，CD平分∠ECB，交过点B 的射线于D，交AB于F，且BC＝BD。

若AE＝9，CE＝12，求BF的长。

4.已知：如图，AF为△ABC的角平分线，以BC为直径的圆与边AB交于点D，点E为弧BD的中点，连接CE交AB于H，交AF于G，AH＝AC，若AC＝6，AB＝10，求EC 的长。

5.如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F，切点为G，连接AG交CD于K，若KG2＝KD·GE，sinE＝35，AK＝23，求FG的长。

6.在⊙O中，直径AB＝2，D为圆上的一点，tan∠BAD＝12，延长AD至点C，使CD＝55，连结BD，H为直径AB上一点，过点H作AB的垂线交⊙O于点E，交射线BD于点F，连结CF。

⑴求证：BC与⊙O相切；⑵当BH等于多少时，△BCF为等腰三角形？⑶当BH等于多少时，CF⊥AE。

【作业】1．如图，在△ABC中，∠B=45°，∠ACB=60°，AB=3，点D为BA延长线上的一点，且∠D=∠ACB，⊙O为△ACD的外接圆。

（1）求BC的长；（2）求⊙O的半径。

2.如图，在△ABC中，以AC为直径的⊙O交BC于点D，作BG⊥AC于点G，交⊙O于点E、F；（1）求证：∠EBC=∠DEC；（2）若∠ABC=45°，⊙O的直径等于5，BD=4，求CG的长。

【选做】已知：如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点B作⊙O的切线，交OD的延长线于点E，连接BE。

连接AD并延长交BE于点F，若OB＝9，sin∠ABC＝23，求BF的长。

第一讲 ───垂直平分线与角平分线 第二讲 ───等腰三角形第三讲 ───平行四边形的性质与判定 第四讲 ───菱形的性质与判定 第五讲 ───矩形的性质与判定第六讲 ───平行四边形和特殊平行四边形性质的应用 第七讲 ───中垂线角平分线复习题 第八讲 ───梯 形第九讲 ───二次函数c ax y +=2的图象 第十讲 ───二次函数y=ax 2的图象与性质 第十一讲 ───二次函数y=ax 2+bx+c 的性质与图象第十二讲 ───二次函数的最值问题第一讲───垂直平分线与角平分线【知识要点：】Ⅰ.线段的垂直平分线定理：线段的垂直平分线上任意一点到这条线段两个端点的距离都相等。

线段的垂直平分线逆定理：若一个点到线段的两个端点的距离相等，则它必在线段的垂直平分线上。

Ⅱ.三角形三边的垂直平分线的性质：三角形三边的垂直平分线的交点到三个顶点的距离相等。

Ⅲ.角平分线性质定理：角平分线上的点到这个角的两边的距离相等。

（注：距离是指角平分线上任一点到这个角的两边所作的垂线段的长度。

）角平分线性质定理的逆定理：若某点到一个角的两边距离相等，则该点在这个角的平分线上。

Ⅳ.三角形三角的角平分线的性质：三角形三角的角平分线的交点到三边的距离相等。

【经典例题：】例1.如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC，求证：AM平分∠DAB.例2．如右图，已知ABCABC，AD是BC边上的高，E是AD上一点，ED=CD，∆中，BA=BC，︒∠45=连接EC。

求证：EA=EC。

例3.如右图，已知AD 是ABC ∆的角平分线，DE 、DF 分别是ABD ∆和ACD ∆的高，DE=DF 。

求证：AD 垂直平分EF 。

例4．如图，ABC ∆是等腰直角三角形，AB=AC ，D 是斜边上BC 的中点，E 、F 分别是AB 、AC 边上的点，且DE ⊥DF ，若BE=12，CF=5，求EF 的长．例5．如右图，四边形ABCD 中，︒=∠=∠90ACB ADB ，E ，F 分别是DC 、AB 的中点，连接DF 、CF ，观察图形：（1）DF 和CF 相等吗？为什么？（2）EF 是否垂直平分DC ，请说明理由。