习题册答案2-2

第二章带传动和链传动§２-２V带传动一、填空题1.V2.V其两侧面之间的夹角通常为根据抗拉3.V带型号有4.V带表面上印有Z1400GB/T11544-2012，它表示该V带是5.V6.为了保证满足正常传动要求，V带传动比一般不大于7.V带轮的轮槽角一般取8.V9.10.安装V二、判断题（X）1.V带的横截面为等腰梯形，其楔角为34°～38°。

（?）2.绳芯结构的V带柔韧性好，适用于转速较高的场合。

（?）3.在一组V带中，若有一根损坏，必须成组更换。

（?）4.V带传动时，两轮的转向相同。

（X）5.V带传动是依靠带的内表面与带轮接触产生摩擦力来传递运动和动力的。

（?）6.V带传动不能用于两轴线空间交错的传动场合。

（?）7.关于i≠1的带传动，两带轮直径不变，中心距越大，小带轮的包角就越大。

（?）8.限制普通V带传动中带轮最小基准直径的主要目的是减小传动时V带的弯曲成以提高V带的使用寿命。

（?）9.考虑到V带弯曲时横截面的变形，带轮的轮槽角应小于V带的楔角。

二、选择题1.V带传动的包角通常要求(?A?)?120°。

A.大于等于??B.等于??C.小于等于2.在中心距不变的情况下，两带轮直径差越大，小带轮的包角(?B?)?A.越大??B.越小??C.不变3.为了便于使用，取V带的(C)?作为它的标记长度。

A.内周长度??B.外周长度??C.基准长度4.带轮直径越小，带的使用寿命就越(?A?)。

A.短??B.长??C.不影响5.如下图所示，V带在带轮轮槽中的正确位置是（A）。

ABC6.下图所示V带传动中，属于正确使用张紧轮的是（C松边、内侧、近大轮）。

7.带轮基准直径大于300mm时，可采用（C）V带轮。

A．实心式B.孔板式C.轮辐式8.实践证明，在中等中心距情况下，V带安装后，用大拇指能将带按下（B）mm左右，则张紧程度合适。

A．5B.15C.25.四、名词解释1.V带节线---当V带垂直其底边弯曲时，在带中保持原长度不变的任一条周线称为V带的节线。

新课程数学选修2（一）—2第一章课后习题解答第一章 导数及其应用 3．1变化率与导数 练习（P6）在第3 h 和5 h 时，原油温度的瞬时变化率分别为1-和3. 它说明在第3 h 附近，原油温度大约以1 ℃／h 的速度下降；在第5 h 时，原油温度大约以3 ℃／h 的速率上升.练习（P8）函数()h t 在3t t =附近单调递增，在4t t =附近单调递增. 并且，函数()h t 在4t 附近比在3t 附近增加得慢. 说明：体会“以直代曲”1的思想. 练习（P9） 函数33()4Vr V π=(05)V ≤≤的图象为根据图象，估算出(0.6)0.3r '≈，(1.2)0.2r '≈.说明：如果没有信息技术，教师可以将此图直接提供给学生，然后让学生根据导数的几何意义估算两点处的导数. 习题1.1 A 组（P10）1、在0t 处，虽然1020()()W t W t =，然而10102020()()()()W t W t t W t W t t t t--∆--∆≥-∆-∆.所以，企业甲比企业乙治理的效率高.说明：平均变化率的应用，体会平均变化率的内涵.2、(1)(1) 4.9 3.3h h t h t t t∆+∆-==-∆-∆∆，所以，(1) 3.3h '=-. 这说明运动员在1t =s 附近以3.3 m ／s 的速度下降. 3、物体在第5 s 的瞬时速度就是函数()s t 在5t =时的导数.(5)(5)10s s t s t t t∆+∆-==∆+∆∆，所以，(5)10s '=. 因此，物体在第 5 s 时的瞬时速度为10 m ／s ，它在第 5 s 的动能213101502k E =⨯⨯= J.4、设车轮转动的角度为θ，时间为t ，则2(0)kt t θ=>. 由题意可知，当0.8t =时，2θπ=. 所以258k π=，于是2258t πθ=.车轮转动开始后第3.2 s 时的瞬时角速度就是函数()t θ在 3.2t =时的导数.(3.2)(3.2)25208t t t t θθθππ∆+∆-==∆+∆∆，所以(3.2)20θπ'=. 因此，车轮在开始转动后第3.2 s 时的瞬时角速度为20π1s -. 说明：第2,3,4题是对了解导数定义及熟悉其符号表示的巩固.5、由图可知，函数()f x 在5x =-处切线的斜率大于零，所以函数在5x =-附近单调递增. 同理可得，函数()f x 在4x =-，2-，0，2附近分别单调递增，几乎没有变化，单调递减，单调递减. 说明：“以直代曲”思想的应用.6、第一个函数的图象是一条直线，其斜率是一个小于零的常数，因此，其导数()f x '的图象如图（1）所示；第二个函数的导数()f x '恒大于零，并且随着x 的增加，()f x '的值也在增加；对于第三个函数，当x 小于零时，()f x '小于零，当x 大于零时，()f x '大于零，并且随着x 的增加，()f x '的值也在增加. 以下给出了满足上述条件的导函数图象中的一种.说明：本题意在让学生将导数与曲线的切线斜率相联系. 习题3.1 B 组（P11）1、高度关于时间的导数刻画的是运动变化的快慢，即速度；速度关于时间的导数刻画的是速度变化的快慢，根据物理知识，这个量就是加速度.2、说明：由给出的()v t 的信息获得()s t 的相关信息，并据此画出()s t 的图象的大致形状. 这个过程基于对导数内涵的了解，以及数与形之间的相互转换.3、由（1）的题意可知，函数()f x 的图象在点(1,5)-处的切线斜率为1-，所以此点附近曲线呈下降趋势. 首先画出切线的图象，然后再画出此点附近函数的图象. 同理可得（2）（3）某点处函数图象的大致形状. 下面是一种参考答案.说明：这是一个综合性问题，包含了对导数内涵、导数几何意义的了解，以及对以直代曲思想的领悟. 本题的答案不唯一. 1．2导数的计算 练习（P18）1、()27f x x '=-，所以，(2)3f '=-，(6)5f '=.2、（1）1ln 2y x '=； （2）2x y e '=； （3）4106y x x '=-； （4）3sin 4cos y x x '=--；（5）1sin 33xy '=-； （6）21y x '=-.习题1.2 A 组（P18）1、()()2S S r r S r r r r r π∆+∆-==+∆∆∆，所以，0()lim(2)2r S r r r r ππ∆→'=+∆=. 2、()9.8 6.5h t t '=-+. 3、3213()34r V Vπ'=.4、（1）213ln 2y x x '=+； （2）1n x n x y nx e x e -'=+； （3）2323sin cos cos sin x x x x xy x -+'=； （4）9899(1)y x '=+； （5）2x y e -'=-； （6）2sin(25)4cos(25)y x x x '=+++. 5、()82f x x '=-+. 由0()4f x '=有 04822x =-+，解得032x =. 6、（1）ln 1y x '=+； （2）1y x =-. 7、1xy π=-+.8、（1）氨气的散发速度()500ln 0.8340.834t A t '=⨯⨯.（2）(7)25.5A '=-，它表示氨气在第7天左右时，以25.5克／天的速率减少. 习题1.2 B 组（P19） 1、（1）（2）当h 越来越小时，sin()sin x h xy h+-=就越来越逼近函数cos y x =.（3）sin y x =的导数为cos y x =.2、当0y =时，0x =. 所以函数图象与x 轴交于点(0,0)P .x y e '=-，所以01x y ='=-.所以，曲线在点P 处的切线的方程为y x =-.2、()4sin d t t '=-. 所以，上午6:00时潮水的速度为0.42-m ／h ；上午9:00时潮水的速度为0.63-m ／h ；中午12:00时潮水的速度为0.83-m ／h ；下午6:00时潮水的速度为 1.24-m ／h.1．3导数在研究函数中的应用 练习（P26）1、（1）因为2()24f x x x =-+，所以()22f x x '=-.当()0f x '>，即1x >时，函数2()24f x x x =-+单调递增； 当()0f x '<，即1x <时，函数2()24f x x x =-+单调递减. （2）因为()x f x e x =-，所以()1x f x e '=-.当()0f x '>，即0x >时，函数()x f x e x =-单调递增；当()0f x '<，即0x <时，函数()x f x e x =-单调递减. （3）因为3()3f x x x =-，所以2()33f x x '=-.当()0f x '>，即11x -<<时，函数3()3f x x x =-单调递增； 当()0f x '<，即1x <-或1x >时，函数3()3f x x x =-单调递减. （4）因为32()f x x x x =--，所以2()321f x x x '=--.当()0f x '>，即13x <-或1x >时，函数32()f x x x x =--单调递增；当()0f x '<，即113x -<<时，函数32()f x x x x =--单调递减.2、3、因为2()(0)f x ax bx c a =++≠，所以()2f x ax b '=+. （1）当0a >时，()0f x '>，即2bx a >-时，函数2()(0)f x ax bx c a =++≠单调递增； ()0f x '<，即2bx a<-时，函数2()(0)f x ax bx c a =++≠单调递减.（2）当0a <时，()0f x '>，即2bx a <-时，函数2()(0)f x ax bx c a =++≠单调递增；()0f x '<，即2bx a >-时，函数2()(0)f x ax bx c a =++≠单调递减.4、证明：因为32()267f x x x =-+，所以2()612f x x x '=-. 当(0,2)x ∈时，2()6120f x x x '=-<，因此函数32()267f x x x =-+在(0,2)内是减函数. 练习（P29）1、24,x x 是函数()y f x =的极值点，其中2x x =是函数()y f x =的极大值点，4x x =是函数()y f x =的极小值点. 2、（1）因为2()62f x x x =--，所以()121f x x '=-.注：图象形状不唯一.令()1210f x x '=-=，得112x =. 当112x >时，()0f x '>，()f x 单调递增；当112x <时，()0f x '<，()f x 单调递减.所以，当112x =时，()f x 有极小值，并且极小值为211149()6()212121224f =⨯--=-. （2）因为3()27f x x x =-，所以2()327f x x '=-. 令2()3270f x x '=-=，得3x =±. 下面分两种情况讨论：①当()0f x '>，即3x <-或3x >时；②当()0f x '<，即33x -<<时. 当x 变化时，()f x '，()f x 变化情况如下表：因此，当3x =-时，()f x 有极大值，并且极大值为54； 当3x =时，()f x 有极小值，并且极小值为54-. （3）因为3()612f x x x =+-，所以2()123f x x '=-. 令2()1230f x x '=-=，得2x =±. 下面分两种情况讨论：①当()0f x '>，即22x -<<时；②当()0f x '<，即2x <-或2x >时. 当x 变化时，()f x '，()f x 变化情况如下表：因此，当2x =-时，()f x 有极小值，并且极小值为10-； 当2x =时，()f x 有极大值，并且极大值为22 （4）因为3()3f x x x =-，所以2()33f x x '=-.令2()330f x x '=-=，得1x =±. 下面分两种情况讨论：①当()0f x '>，即11x -<<时；②当()0f x '<，即1x <-或1x >时. 当x 变化时，()f x '，()f x 变化情况如下表：因此，当1x =-时，()f x 有极小值，并且极小值为2-； 当1x =时，()f x 有极大值，并且极大值为2 练习（P31）（1）在[0,2]上，当112x =时，2()62f x x x =--有极小值，并且极小值为149()1224f =-. 又由于(0)2f =-，(2)20f =.因此，函数2()62f x x x =--在[0,2]上的最大值是20、最小值是4924-. （2）在[4,4]-上，当3x =-时，3()27f x x x =-有极大值，并且极大值为(3)54f -=；当3x =时，3()27f x x x =-有极小值，并且极小值为(3)54f =-； 又由于(4)44f -=，(4)44f =-.因此，函数3()27f x x x =-在[4,4]-上的最大值是54、最小值是54-.（3）在1[,3]3-上，当2x =时，3()612f x x x =+-有极大值，并且极大值为(2)22f =.又由于155()327f -=，(3)15f =.因此，函数3()612f x x x =+-在1[,3]3-上的最大值是22、最小值是5527.（4）在[2,3]上，函数3()3f x x x =-无极值. 因为(2)2f =-，(3)18f =-.因此，函数3()3f x x x =-在[2,3]上的最大值是2-、最小值是18-. 习题1.3 A 组（P31）1、（1）因为()21f x x =-+，所以()20f x '=-<. 因此，函数()21f x x =-+是单调递减函数.（2）因为()cos f x x x =+，(0,)2x π∈，所以()1sin 0f x x '=->，(0,)2x π∈.因此，函数()cos f x x x =+在(0,)2π上是单调递增函数. （3）因为()24f x x =--，所以()20f x '=-<. 因此，函数()24f x x =-是单调递减函数. （4）因为3()24f x x x =+，所以2()640f x x '=+>. 因此，函数3()24f x x x =+是单调递增函数. 2、（1）因为2()24f x x x =+-，所以()22f x x '=+.当()0f x '>，即1x >-时，函数2()24f x x x =+-单调递增. 当()0f x '<，即1x <-时，函数2()24f x x x =+-单调递减. （2）因为2()233f x x x =-+，所以()43f x x '=-.当()0f x '>，即34x >时，函数2()233f x x x =-+单调递增. 当()0f x '<，即34x <时，函数2()233f x x x =-+单调递减.（3）因为3()3f x x x =+，所以2()330f x x '=+>. 因此，函数3()3f x x x =+是单调递增函数. （4）因为32()f x x x x =+-，所以2()321f x x x '=+-. 当()0f x '>，即1x <-或13x >时，函数32()f x x x x =+-单调递增. 当()0f x '<，即113x -<<时，函数32()f x x x x =+-单调递减.3、（1）图略. （2）加速度等于0.4、（1）在2x x =处，导函数()y f x '=有极大值；（2）在1x x =和4x x =处，导函数()y f x '=有极小值； （3）在3x x =处，函数()y f x =有极大值； （4）在5x x =处，函数()y f x =有极小值.5、（1）因为2()62f x x x =++，所以()121f x x '=+. 令()1210f x x '=+=，得112x =-. 当112x >-时，()0f x '>，()f x 单调递增； 当112x <-时，()0f x '<，()f x 单调递减.所以，112x =-时，()f x 有极小值，并且极小值为211149()6()212121224f -=⨯---=-.（2）因为3()12f x x x =-，所以2()312f x x '=-. 令2()3120f x x '=-=，得2x =±. 下面分两种情况讨论：①当()0f x '>，即2x <-或2x >时；②当()0f x '<，即22x -<<时. 当x 变化时，()f x '，()f x 变化情况如下表：因此，当2x =-时，()f x 有极大值，并且极大值为16； 当2x =时，()f x 有极小值，并且极小值为16-. （3）因为3()612f x x x =-+，所以2()123f x x '=-+. 令2()1230f x x '=-+=，得2x =±. 下面分两种情况讨论：①当()0f x '>，即2x <-或2x >时；②当()0f x '<，即22x -<<时. 当x 变化时，()f x '，()f x 变化情况如下表：因此，当2x =-时，()f x 有极大值，并且极大值为22； 当2x =时，()f x 有极小值，并且极小值为10-. （4）因为3()48f x x x =-，所以2()483f x x '=-. 令2()4830f x x '=-=，得4x =±. 下面分两种情况讨论：①当()0f x '>，即2x <-或2x >时；②当()0f x '<，即22x -<<时. 当x 变化时，()f x '，()f x 变化情况如下表：因此，当4x =-时，()f x 有极小值，并且极小值为128-； 当4x =时，()f x 有极大值，并且极大值为128. 6、（1）在[1,1]-上，当112x =-时，函数2()62f x x x =++有极小值，并且极小值为4724. 由于(1)7f -=，(1)9f =，所以，函数2()62f x x x =++在[1,1]-上的最大值和最小值分别为9，4724. （2）在[3,3]-上，当2x =-时，函数3()12f x x x =-有极大值，并且极大值为16；当2x =时，函数3()12f x x x =-有极小值，并且极小值为16-. 由于(3)9f -=，(3)9f =-，所以，函数3()12f x x x =-在[3,3]-上的最大值和最小值分别为16，16-.（3）在1[,1]3-上，函数3()612f x x x =-+在1[,1]3-上无极值.由于1269()327f -=，(1)5f =-，所以，函数3()612f x x x =-+在1[,1]3-上的最大值和最小值分别为26927，5-.（4）当4x =时，()f x 有极大值，并且极大值为128.. 由于(3)117f -=-，(5)115f =，所以，函数3()48f x x x =-在[3,5]-上的最大值和最小值分别为128，117-. 习题3.3 B 组（P32）1、（1）证明：设()sin f x x x =-，(0,)x π∈. 因为()cos 10f x x '=-<，(0,)x π∈ 所以()sin f x x x =-在(0,)π内单调递减因此()sin (0)0f x x x f =-<=，(0,)x π∈，即sin x x <，(0,)x π∈. 图略 （2）证明：设2()f x x x =-，(0,1)x ∈. 因为()12f x x '=-，(0,1)x ∈所以，当1(0,)2x ∈时，()120f x x '=->，()f x 单调递增，2()(0)0f x x x f =->=；当1(,1)2x ∈时，()120f x x '=-<，()f x 单调递减，2()(1)0f x x x f =->=；又11()024f =>. 因此，20x x ->，(0,1)x ∈. 图略（3）证明：设()1x f x e x =--，0x ≠. 因为()1x f x e '=-，0x ≠所以，当0x >时，()10x f x e '=->，()f x 单调递增，()1(0)0x f x e x f =-->=；当0x <时，()10x f x e '=-<，()f x 单调递减，()1(0)0x f x e x f =-->=；综上，1x e x ->，0x ≠. 图略（4）证明：设()ln f x x x =-，0x >. 因为1()1f x x'=-，0x ≠ 所以，当01x <<时，1()10f x x'=->，()f x 单调递增， ()ln (1)10f x x x f =-<=-<； 当1x >时，1()10f x x'=-<，()f x 单调递减， ()ln (1)10f x x x f =-<=-<；当1x =时，显然ln11<. 因此，ln x x <. 由（3）可知，1x e x x >+>，0x >. . 综上，ln x x x e <<，0x >图略2、（1）函数32()f x ax bx cx d =+++的图象大致是个“双峰”图象，类似“”或“”的形状. 若有极值，则在整个定义域上有且仅有一个极大值和一个极小值，从图象上能大致估计它的单调区间.（2）因为32()f x ax bx cx d =+++，所以2()32f x ax bx c '=++. 下面分类讨论：当0a ≠时，分0a >和0a <两种情形： ①当0a >，且230b ac ->时，设方程2()320f x ax bx c '=++=的两根分别为12,x x ，且12x x <，当2()320f x ax bx c '=++>，即1x x <或2x x >时，函数32()f x ax bx cx d =+++单调递增；当2()320f x ax bx c '=++<，即12x x x <<时，函数32()f x ax bx cx d =+++单调递减.当0a >，且230b ac -≤时，此时2()320f x ax bx c '=++≥，函数32()f x ax bx cx d =+++单调递增. ②当0a <，且230b ac ->时，设方程2()320f x ax bx c '=++=的两根分别为12,x x ，且12x x <，当2()320f x ax bx c '=++>，即12x x x <<时，函数32()f x ax bx cx d =+++单调递增；当2()320f x ax bx c '=++<，即1x x <或2x x >时，函数32()f x ax bx cx d =+++单调递减.当0a <，且230b ac -≤时，此时2()320f x ax bx c '=++≤，函数32()f x ax bx cx d =+++单调递减 1．4生活中的优化问题举例 习题1.4 A 组（P37）1、设两段铁丝的长度分别为x ，l x -，则这两个正方形的边长分别为4x ，4l x -，两个正方形的面积和为 22221()()()(22)4416x l x S f x x lx l -==+=-+，0x l <<.令()0f x '=，即420x l -=，2lx =.当(0,)2l x ∈时，()0f x '<；当(,)2lx l ∈时，()0f x '>.因此，2lx =是函数()f x 的极小值点，也是最小值点.所以，当两段铁丝的长度分别是2l时，两个正方形的面积和最小.2、如图所示，由于在边长为a 的正方形铁片的四角截去 四个边长为x 的小正方形，做成一个无盖方盒，所以无 盖方盒的底面为正方形，且边长为2a x -，高为x .（1）无盖方盒的容积2()(2)V x a x x =-，02ax <<.（2）因为322()44V x x ax a x =-+， 所以22()128V x x ax a '=-+.令()0V x '=，得2a x =（舍去），或6a x =. 当(0,)6a x ∈时，()0V x '>；当(,)62a ax ∈时，()0V x '<.因此，6ax =是函数()V x 的极大值点，也是最大值点.所以，当6ax =时，无盖方盒的容积最大.3、如图，设圆柱的高为h ，底半径为R ， 则表面积222S Rh R ππ=+ 由2V R h π=，得2V h Rπ=. （第2题）因此，2222()222V V S R R R R R Rππππ=+=+，0R >. 令2()40V S R R R π'=-+=，解得R =.当R ∈时，()0S R '<；当)R ∈+∞时，()0S R '>. 因此，R =是函数()S R 的极小值点，也是最小值点. 此时，22V h R R π===. 所以，当罐高与底面直径相等时，所用材料最省.4、证明：由于211()()n i i f x x a n ==-∑，所以12()()n i i f x x a n ='=-∑.令()0f x '=，得11ni i x a n ==∑，可以得到，11ni i x a n ==∑是函数()f x 的极小值点，也是最小值点.这个结果说明，用n 个数据的平均值11ni i a n =∑表示这个物体的长度是合理的，这就是最小二乘法的基本原理.5、设矩形的底宽为x m ，则半圆的半径为2xm ，半圆的面积为28x π2m ，矩形的面积为28x a π-2m ，矩形的另一边长为()8a xx π-m 因此铁丝的长为22()(1)244xa x a l x x x x x πππ=++-=++，0x <<令22()104a l x x π'=+-=，得x =.当x ∈时，()0l x '<；当x ∈时，()0l x '>.因此，x =()l x 的极小值点，也是最小值点.时，所用材料最省. 6、利润L 等于收入R 减去成本C ，而收入R 等于产量乘单价. 由此可得出利润L 与产量q 的函数关系式，再用导数求最大利润.收入211(25)2588R q p q q q q =⋅=-=-，利润2211(25)(1004)2110088L R C q q q q q =-=--+=-+-，0200q <<.求导得1214L q '=-+令0L '=，即12104q -+=，84q =.当(0,84)q ∈时，0L '>；当(84,200)q ∈时，0L '<；因此，84q =是函数L 的极大值点，也是最大值点.所以，产量为84时，利润L 最大,习题1.4 B 组（P37）1、设每个房间每天的定价为x 元，那么宾馆利润21801()(50)(20)7013601010x L x x x x -=--=-+-，180680x <<.令1()7005L x x '=-+=，解得350x =.当(180,350)x ∈时，()0L x '>；当(350,680)x ∈时，()0L x '>. 因此，350x =是函数()L x 的极大值点，也是最大值点.所以，当每个房间每天的定价为350元时，宾馆利润最大. 2、设销售价为x 元／件时，利润4()()(4)()(5)b x L x x a c cc x a x b b-=-+⨯=--，54b a x <<. 令845()0c ac bc L x x b b+'=-+=，解得458a bx +=.当45(,)8a b x a +∈时，()0L x '>；当455(,)84a b bx +∈时，()0L x '<.当458a bx +=是函数()L x 的极大值点，也是最大值点. 所以，销售价为458a b+元／件时，可获得最大利润.1．5定积分的概念 练习（P42） 83. 说明：进一步熟悉求曲边梯形面积的方法和步骤，体会“以直代曲”和“逼近”的思想.练习（P45）1、22112()[()2]()i i i i i s s v t n n n n n n '∆≈∆=∆=-+⋅=-⋅+⋅，1,2,,i n =.于是 111()n n ni i i i i is s s v t n ==='=∆≈∆=∆∑∑∑2112[()]ni i n n n ==-⋅+⋅∑22211111()()()2n n n n n n n n -=-⋅--⋅-⋅+2231[12]2n n=-++++31(1)(21)26n n n n ++=-⋅+111(1)(1)232n n =-+++取极值，得1111115lim [()]lim [(1)(1)2]323nnn n i i i s v n n n n →∞→∞====-+++=∑∑ 说明：进一步体会“以不变代变”和“逼近”的思想. 2、223km.说明：进一步体会“以不变代变”和“逼近”的思想，熟悉求变速直线运动物体路程的方法和步骤. 练习（P48）2304x dx =⎰. 说明：进一步熟悉定积分的定义和几何意义.从几何上看，表示由曲线3y x =与直线0x =，2x =，0y =所围成的曲边梯形的面积4S =.习题1.5 A 组（P50）1、（1）10021111(1)[(1)1]0.495100100i i x dx =--≈+-⨯=∑⎰； （2）50021111(1)[(1)1]0.499500500i i x dx =--≈+-⨯=∑⎰； （3）100021111(1)[(1)1]0.499510001000i i x dx =--≈+-⨯=∑⎰. 说明：体会通过分割、近似替换、求和得到定积分的近似值的方法.2、距离的不足近似值为：18112171310140⨯+⨯+⨯+⨯+⨯=（m ）； 距离的过剩近似值为：271181121713167⨯+⨯+⨯+⨯+⨯=（m ）.3、证明：令()1f x =. 用分点 011i i n a x x x x x b -=<<<<<<=将区间[,]a b 等分成n 个小区间，在每个小区间1[,]i i x x -上任取一点(1,2,,)i i n ξ=作和式 11()nni i i b af x b a nξ==-∆==-∑∑， 从而 11lim nban i b adx b a n→∞=-==-∑⎰， 说明：进一步熟悉定积分的概念. 4、根据定积分的几何意义，0⎰表示由直线0x =，1x =，0y =以及曲线y =所围成的曲边梯形的面积，即四分之一单位圆的面积，因此4π=⎰.5、（1）03114x dx -=-⎰. 由于在区间[1,0]-上30x ≤，所以定积分031x dx -⎰表示由直线0x =，1x =-，0y =和曲线3y x =所围成的曲边梯形的面积的相反数.（2）根据定积分的性质，得10133311011044x dx x dx x dx --=+=-+=⎰⎰⎰.由于在区间[1,0]-上30x ≤，在区间[0,1]上30x ≥，所以定积分131x dx -⎰等于位于x轴上方的曲边梯形面积减去位于x 轴下方的曲边梯形面积.（3）根据定积分的性质，得202333110115444x dx x dx x dx --=+=-+=⎰⎰⎰由于在区间[1,0]-上30x ≤，在区间[0,2]上30x ≥，所以定积分231x dx -⎰等于位于x轴上方的曲边梯形面积减去位于x 轴下方的曲边梯形面积.说明：在（3）中，由于3x 在区间[1,0]-上是非正的，在区间[0,2]上是非负的，如果直接利用定义把区间[1,2]-分成n 等份来求这个定积分，那么和式中既有正项又有负项，而且无法抵挡一些项，求和会非常麻烦. 利用性质3可以将定积分231x dx-⎰化为02331x dx x dx -+⎰⎰，这样，3x 在区间[1,0]-和区间[0,2]上的符号都是不变的，再利用定积分的定义，容易求出031x dx -⎰，230x dx ⎰，进而得到定积分231x dx -⎰的值. 由此可见，利用定积分的性质可以化简运算.在（2）（3）中，被积函数在积分区间上的函数值有正有负，通过练习进一步体会定积分的几何意义. 习题1.5 B 组（P50）1、该物体在0t =到6t =（单位：s ）之间走过的路程大约为145 m.说明：根据定积分的几何意义，通过估算曲边梯形内包含单位正方形的个数来估计物体走过的路程. 2、（1）9.81v t =.（2）过剩近似值：8111899.819.8188.292242i i =⨯⨯⨯=⨯⨯=∑（m ）； 不足近似值：81111879.819.8168.672242i i =-⨯⨯⨯=⨯⨯=∑（m ） （3）49.81tdt ⎰； 49.81d 78.48t t =⎰（m ）.3、（1）分割在区间[0,]l 上等间隔地插入1n -个分点，将它分成n 个小区间：[0,]l n ，2[,]l l n n ，……，(2)[,]n l l n -， 记第i 个区间为(1)[,]i l iln n-（1,2,i n =），其长度为 (1)il i l l x n n n-∆=-=.把细棒在小段[0,]l n ，2[,]l l n n ，……，(2)[,]n ll n-上质量分别记作： 12,,,n m m m ∆∆∆，则细棒的质量1ni i m m ==∆∑.（2）近似代替当n 很大，即x ∆很小时，在小区间(1)[,]i l iln n-上，可以认为线密度2()x x ρ=的值变化很小，近似地等于一个常数，不妨认为它近似地等于任意一点(1)[,]i i l il n n ξ-∈处的函数值2()i i ρξξ=. 于是，细棒在小段(1)[,]i l il n n-上质量2()i i i lm x nρξξ∆≈∆=（1,2,i n =）.（3）求和得细棒的质量 2111()nnni i i i i i l m m x nρξξ====∆≈∆=∑∑∑. （4）取极限细棒的质量 21lim ni n i lm nξ→∞==∑，所以20l m x dx =⎰..1．6微积分基本定理练习（P55） （1）50； （2）503； （3）533-； （4）24； （5）3ln 22-； （6）12； （7）0； （8）2-.说明：本题利用微积分基本定理和定积分的性质计算定积分. 习题1.6 A 组（P55）1、（1）403； （2）13ln 22--； （3）9ln 3ln 22+-；（4）176-； （5）2318π+； （6）22ln 2e e --. 说明：本题利用微积分基本定理和定积分的性质计算定积分.2、3300sin [cos ]2xdx x ππ=-=⎰.它表示位于x 轴上方的两个曲边梯形的面积与x 轴下方的曲边梯形的面积之差. 或表述为：位于x 轴上方的两个曲边梯形的面积（取正值）与x 轴下方的曲边梯形的面积（取负值）的代数和. 习题1.6 B 组（P55）1、（1）原式＝221011[]222x e e =-； （2）原式＝4611[sin 2]22x ππ=； （3）原式＝3126[]ln 2ln 2x =.2、（1）cos 1sin [][cos cos()]0mx mxdx m m m m ππππππ--=-=---=⎰；（2）sin 1cos [sin sin()]0mx mxdx m m m m ππππππ--=|=--=⎰；（3）21cos 2sin 2sin []224mx x mx mxdx dx m πππππππ----==-=⎰⎰；（4）21cos 2sin 2cos []224mx x mx mxdx dx mπππππππ---+==+=⎰⎰.3、（1）0.202220()(1)[]49245245t kt kt t kt t g g g g g gs t e dt t e t e t e k k k k k k----=-=+=+-=+-⎰.（2）由题意得 0.2492452455000t t e -+-=.这是一个超越方程，为了解这个方程，我们首先估计t 的取值范围. 根据指数函数的性质，当0t >时，0.201t e -<<，从而 5000495245t <<， 因此，500052454949t <<. 因此50000.2749245 3.3610e-⨯-≈⨯，52450.2749245 1.2410e-⨯-≈⨯，所以，70.271.2410245 3.3610t e ---⨯<<⨯.从而，在解方程0.2492452455000t t e -+-=时，0.2245t e -可以忽略不计.因此，.492455000t -≈，解之得 524549t ≈（s ）. 说明：B 组中的习题涉及到被积函数是简单的复合函数的定积分，可视学生的具体情况选做，不要求掌握. 1．7定积分的简单应用 练习（P58）（1）323； （2）1.说明：进一步熟悉应用定积分求平面图形的面积的方法与求解过程. 练习（P59）1、52533(23)[3]22s t dt t t =+=+=⎰（m ）.2、42403(34)[4]402W x dx x x =+=+=⎰（J ）. 习题1.7 A 组（P60）1、（1）2； （2）92.2、2[]b b a a q q q qW k dr k k k r r a b==-=-⎰. 3、令()0v t =，即40100t -=. 解得4t =. 即第4s 时物体达到最大高度.最大高度为 424(4010)[405]80h t dt t t =-=-=⎰（m ）. 4、设t s 后两物体相遇，则 2(31)105ttt dt tdt +=+⎰⎰，解之得5t =. 即,A B 两物体5s 后相遇.此时，物体A 离出发地的距离为 523500(31)[]130t dt t t +=+=⎰（m ）.5、由F kl =，得100.01k =. 解之得1000k =. 所做的功为 0.120.10010005005W ldl l ==|=⎰（J ）.6、（1）令55()501v t t t=-+=+，解之得10t =. 因此，火车经过10s 后完全停止. （2）1021000551(5)[555ln(1)]55ln1112s t dt t t t t =-+=-++=+⎰（m ）. 习题1.7 B 组（P60）1、（1）22a aa x dx --⎰表示圆222x y a +=与x 轴所围成的上半圆的面积，因此2222aaa a x dx π--=⎰（2）120[1(1)]x x dx ---⎰表示圆22(1)1x y -+=与直线y x =所围成的图形（如图所示）的面积，因此，2120111[1(1)]114242x x dx ππ⨯---=-⨯⨯=-⎰. 2、证明：建立如图所示的平面直角坐标系，可设抛物线的方程为2y ax =，则2()2b h a =⨯，所以24ha b =.从而抛物线的方程为 224hy x b =.于是，抛物线拱的面积232202204422()2[]33b b h h S h x dx hx x bh b b =-=-=⎰. 3、如图所示.解方程组223y x y x⎧=+⎨=⎩得曲线22y x =+与曲线3y x =交点的横坐标11x =，22x =. 于是，所求的面积为122201[(2)3][3(2)]1x x dx x x dx +-+-+=⎰⎰.y xO1（第1（2）题）yxh b O （第2题）4、证明：2[]()R hR h R RMm Mm MmhW Gdr G G r r R R h ++==-=+⎰. 第一章 复习参考题A 组（P65）1、（1）3； （2）4y =-.2、（1）22sin cos 2cos x x xy x+'=； （2）23(2)(31)(53)y x x x '=-+-； （3）22ln ln 2x xy x x '=+； （4）2422(21)x x y x -'=+. 3、32GMm F r '=-. 4、（1）()0f t '<. 因为红茶的温度在下降.（2）(3)4f '=-表明在3℃附近时，红茶温度约以4℃／min 的速度下降. 图略.5、因为()f x =()f x '=.当()0f x '=>，即0x >时，()f x 单调递增；当()0f x '=<，即0x <时，()f x 单调递减.6、因为2()f x x px q =++，所以()2f x x p '=+. 当()20f x x p '=+=，即12px =-=时，()f x 有最小值. 由12p-=，得2p =-. 又因为(1)124f q =-+=，所以5q =. 7、因为2322()()2f x x x c x cx c x =-=-+， 所以22()34(3)()f x x cx c x c x c '=-+=--. 当()0f x '=，即3cx =，或x c =时，函数2()()f x x x c =-可能有极值. 由题意当2x =时，函数2()()f x x x c =-有极大值，所以0c >.由于 所以，当3c x =时，函数2()()f x x x c =-有极大值. 此时，23c=，6c =. 8、设当点A 的坐标为(,0)a 时，AOB ∆的面积最小. 因为直线AB 过点(,0)A a ，(1,1)P ，所以直线AB 的方程为001y x a x a--=--，即1()1y x a a =--. 当0x =时，1a y a =-，即点B 的坐标是(0,)1aa -. 因此，AOB ∆的面积21()212(1)AOBa a S S a a a a ∆===--.令()0S a '=，即2212()02(1)a aS a a -'=⋅=-. 当0a =，或2a =时，()0S a '=，0a =不合题意舍去. 由于 所以，当2a =，即直线的倾斜角为时，的面积最小，最小面积为2. 9、D .10、设底面一边的长为x m ，另一边的长为(0.5)x +m. 因为钢条长为14.8m. 所以，长方体容器的高为14.844(0.5)12.88 3.2244x x xx --+-==-.设容器的容积为V ，则32()(0.5)(3.22)2 2.2 1.6V V x x x x x x x ==+-=-++，0 1.6x <<.令()0V x '=，即26 4.4 1.60x x -++=. 所以，415x =-（舍去），或1x =. 当(0,1)x ∈时，()0V x '>；当(1,1.6)x ∈时，()0V x '<. 因此，1x =是函数()V x 在(0,1.6)的极大值点，也是最大值点. 所以，当长方体容器的高为1 m 时，容器最大，最大容器为1.8 m 3.11、设旅游团人数为100x +时，旅行社费用为2()(100)(10005)5500100000y f x x x x ==+-=-++(080)x ≤≤. 令()0f x '=，即105000x -+=，50x =.又(0)100000f =，(80)108000f =，(50)112500f =. 所以，50x =是函数()f x 的最大值点.所以，当旅游团人数为150时，可使旅行社收费最多. 12、设打印纸的长为x cm 时，可使其打印面积最大.因为打印纸的面积为623.7，长为x ，所以宽为623.7x，打印面积623.7()(2 2.54)(2 3.17)S x x x=-⨯-⨯23168.396655.9072 6.34x x=--，5.0898.38x <<. 令()0S x '=，即23168.3966.340x -=，22.36x ≈（负值舍去），623.727.8922.36≈. 22.36x =是函数()S x 在(5.08,98.38)内唯一极值点，且为极大值，从而是最大值点.所以，打印纸的长、宽分别约为27.89cm ，22.36cm 时，可使其打印面积最大. 13、设每年养q 头猪时，总利润为y 元.则 21()20000100300200002y R q q q q =--=-+-(0400,)q q N <≤∈.令0y '=，即3000q -+=，300q =.当300q =时，25000y =；当400q =时，20000y =.300q =是函数()y p 在(0,400]内唯一极值点，且为极大值点，从而是最大值点. 所以，每年养300头猪时，可使总利润最大，最大总利润为25000元.14、（1）2； （2）22e -； （3）1；（4）原式＝22222000cos sin (cos sin )[sin cos ]0cos sin x x dx x x dx x x x xπππ-=-=+=+⎰⎰；（5）原式＝22001cos sin 2[]224x x x dx πππ---==⎰.15、略. 说明：利用函数图象的对称性、定积分的几何意义进行解释.16、2.17、由F kl =，得0.0490.01k =. 解之得 4.9k =.所做的功为 20.30.30.10.14.9 4.90.1962l W ldl ==⨯|=⎰（J ）第一章 复习参考题B 组（P66）1、（1）43()10210b t t '=-⨯. 所以，细菌在5t =与10t =时的瞬时速度分别为0和410-.（2）当05t ≤<时，()0b t '>，所以细菌在增加；当55t <<+()0b t '<，所以细菌在减少.2、设扇形的半径为r ，中心角为α弧度时，扇形的面积为S .因为212S r α=，2l r r α-=，所以2lrα=-.222111(2)(2)222l S r r lr r r α==-=-，02l r <<.令0S '=，即40l r -=，4lr =，此时α为2弧度.4lr =是函数()S r 在(0,)2l 内唯一极值点，且是极大值点，从而是最大值点.所以，扇形的半径为4l、中心角为2弧度时，扇形的面积最大.3、设圆锥的底面半径为r ，高为h ，体积为V ，那么222r h R +=.因此，222231111()3333V r h R h h R h h ππππ==-=-，0h R <<.令22103V R h ππ'=-=，解得h =.容易知道，h =是函数()V h 的极大值点，也是最大值点.所以，当h R =时，容积最大.把3h R =代入222r h R +=，得3r R =.由2R r απ=，得3α=.所以，圆心角为α=时，容积最大. 4、由于28010k =⨯，所以45k =. 设船速为x km ／h 时，总费用为y ，则2420204805y x x x=⨯+⨯ 960016x x=+，0x > 令0y '=，即29600160x -=，24x ≈.容易知道，24x =是函数y 的极小值点，也是最小值点.当24x =时，960020(1624)()9412424⨯+÷≈（元／时） 所以，船速约为24km ／h 时，总费用最少，此时每小时费用约为941元.5、设汽车以x km ／h 行驶时，行车的总费用2390130(3)14360x y x x=++⨯，50100x ≤≤令0y '=，解得53x ≈（km ／h ）. 此时，114y ≈（元） 容易得到，53x ≈是函数y 的极小值点，也是最小值点.因此，当53x ≈时，行车总费用最少.所以，最经济的车速约为53km ／h ；如果不考虑其他费用，这次行车的总费用约是114元.6、原式＝4404422022[]2xxx x x e dx e dx e dx e e e e -----=+=-+|=+-⎰⎰⎰.7、解方程组 2y kx y x x=⎧⎨=-⎩ 得，直线y kx =与抛物线2y x x =-交点的横坐标为0x =，1k -.抛物线与x 轴所围图形的面积2312100111()[]23236x x S x x dx =-=-=-=⎰.由题设得11200()2k k Sx x dx kxdx --=--⎰⎰31221001()[]23kkk x x x kx dx x ---=--=-⎰3(1)6k -=.又因为16S =，所以31(1)2k -=.于是1k =说明：本题也可以由面积相等直接得到111220()()kk k x x kx dx kxdx x x dx -----=+-⎰⎰⎰，由此求出k 的值. 但计算较为烦琐.新课程数学选修2—2第二章课后习题解答第二章推理与证明2．1合情推理与演绎推理 练习（P77）1、由12341a a a a ====，猜想1n a =.2、相邻两行数之间的关系是：每一行首尾的数都是1，其他的数都等于上一行中与之相邻的两个数的和.3、设111O PQ R V -和222O P Q R V -分别是四面体111O PQ R -和222O P Q R -的体积， 则111222111222O PQR O P Q R V OP OQ OR V OP OQ OR --=⋅⋅. 练习（P81） 1、略.2、因为通项公式为n a 的数列{}n a ， 若1n na p a +=，其中p 是非零常数，则{}n a 是等比数列；……………………大前提 又因为0cq ≠，则0q ≠，则11n n nn a cq q a cq++==；……………………………小前提 所以，通项公式为(0)n n a cq cq =≠的数列{}n a 是等比数列. ……………………结论 3、由AD BD >，得到ACD BCD ∠>∠的推理是错误的. 因为这个推理的大前提是“在同一个三角形中，大边对大角”，小前提是“AD BD >”，而AD 与BD 不在同一个三角形中.习题2.1 A 组（P83）1、21n a n =+()n N *∈. 2、2F V E +=+.3、当6n ≤时，122(1)n n -<+；当7n =时，122(1)n n -=+；当8n =时，122(1)n n ->+()n N *∈.4、212111(2)n n A A A n π++≥-（2n >，且n N *∈）. 5、121217n n b b b b b b -=（17n <，且n N *∈）.6、如图，作DE ∥AB 交BC 于E .因为两组对边分别平行的四边形是平行四边形， 又因为AD ∥BE ，AB ∥DE . 所以四边形ABED 是平行四边形.因为平行四边形的对边相等.又因为四边形ABED 是平行四边形. 所以AB DE =.因为与同一条线段等长的两条线段的长度相等，又因为AB DE =，AB DC =, 所以DE DC = 因为等腰三角形的两底角是相等的.又因为△DEC 是等腰三角形, 所以DEC C ∠=∠ 因为平行线的同位角相等又因为DEC ∠与B ∠是平行线AB 和DE 的同位角, 所以DEC B ∠=∠ 因为等于同角的两个角是相等的，又因为DEC C ∠=∠，DEC B ∠=∠, 所以B C ∠=∠ 习题2.1 B 组（P84）1、由123S =-，234S =-，345S =-，456S =-，567S =-，猜想12n n S n +=-+.2、略.3、略.2．2直接证明与间接证明 练习（P89）1、因为442222cos sin (cos sin )(cos sin )cos 2θθθθθθθ-=+-=，所以，命题得证. 2>，只需证22>，即证1313+>+>，只需要22>，即证4240>，这是显然成立的. 所以，命题得证. 3、因为222222222()()()(2sin )(2tan )16sin tan a b a b a b αααα-=-+==， 又因为sin (1cos )sin (1cos )1616(tan sin )(tan sin )16cos cos ab αααααααααα+-=+-=⋅22222222sin (1cos )sin sin 161616sin tan cos cos αααααααα-===， 从而222()16a b ab -=，所以，命题成立.说明：进一步熟悉运用综合法、分析法证明数学命题的思考过程与特点.（第6练习（P91）1、假设B ∠不是锐角，则90B ∠≥︒. 因此9090180C B ∠+∠≥︒+︒=︒. 这与三角形的内角和等于180°矛盾.所以，假设不成立. 从而，B ∠一定是锐角.2成等差数列，则=所以22=，化简得5=225=，即2540=， 这是不可能的. 所以，假设不成立..说明：进一步熟悉运用反证法证明数学命题的思考过程与特点. 习题2.2 A 组（P91）1、由于0a ≠，因此方程至少有一个跟bx a=.假设方程不止一个根，则至少有两个根，不妨设12,x x 是它的两个不同的根，则1ax b =①2ax b =②①－②得12()0a x x -=因为12x x ≠，所以120x x -≠，从而0a =，这与已知条件矛盾，故假设不成立. 2、因为(1tan )(1tan )2A B ++=展开得1tan tan tan tan 2A B A B +++=，即tan tan 1tan tan A B A B +=-. ①假设1tan tan 0A B -=，则cos cos sin sin 0cos cos A B A B A B -=，即cos()0cos cos A B A B += 所以cos()0A B +=.因为A ，B 都是锐角，所以0A B π<+<，从而2A B π+=，与已知矛盾.因此1tan tan 0A B -≠.①式变形得tan tan 11tan tan A BA B +=-，即tan()1A B +=.又因为0A B π<+<，所以4A B π+=. 说明：本题也可以把综合法和分析法综合使用完成证明.3、因为1tan 12tan αα-=+，所以12tan 0α+=，从而2sin cos 0αα+=.另一方面，要证3sin 24cos2αα=-，只要证226sin cos 4(cos sin )αααα=-- 即证222sin 3sin cos 2cos 0αααα--=， 即证(2sin cos )(sin 2cos )0αααα+-=由2sin cos 0αα+=可得，(2sin cos )(sin 2cos )0αααα+-=，于是命题得证. 说明：本题可以单独使用综合法或分析法进行证明，但把综合法和分析法结合使用进行证明的思路更清晰.4、因为,,a b c 的倒数成等差数列，所以211b ac =+.假设2B π<不成立，即2B π≥，则B 是ABC ∆的最大内角，所以,b a b c >>（在三角形中，大角对大边）， 从而11112a c b b b +>+=. 这与211b a c=+矛盾. 所以，假设不成立，因此，2B π<.习题2.2 B 组（P91）1、要证2s a <，由于22s ab <，所以只需要2s s b<，即证b s <.因为1()2s a b c =++，所以只需要2b a b c <++，即证b a c <+. 由于,,a b c 为一个三角形的三条边，所以上式成立. 于是原命题成立. 2、由已知条件得2b ac =①2x a b =+，2y b c =+②要证2a cx y+=，只要证2ay cx xy +=，只要证224ay cx xy += 由①②，得22()()2ay cx a b c c a b ab ac bc +=+++=++，24()()2xy a b b c ab b ac bc ab ac bc =++=+++=++， 所以，224ay cx xy +=，于是命题得证. 3、由tan()2tan αβα+=得sin()2sin cos()cos αβααβα+=+，即sin()cos 2cos()sin αβααβα+=+. ……①要证3sin sin(2)βαβ=+即证3sin[()]sin[()]αβααβα+-=++即证3[sin()cos cos()sin ]sin()cos cos()sin αβααβααβααβα+-+=+++ 化简得sin()cos 2cos()sin αβααβα+=+，这就是①式.所以，命题成立.说明：用综合法和分析法证明命题时，经常需要把两者结合起来使用. 2．3数学归纳法 练习（P95）1、先证明：首项是1a ，公差是d 的等差数列的通项公式是1(1)n a a n d =+-. （1）当1n =时，左边＝1a ，右边＝11(11)a d a +-=， 因此，左边＝右边. 所以，当1n =时命题成立. （2）假设当n k =时，命题成立，即1(1)k a a k d =+-. 那么，11(1)[(1)1]k k k a a d a k d d a k d +=+=+-+=++-. 所以，当1n k =+时，命题也成立.根据（1）和（2），可知命题对任何n N *∈都成立.再证明：该数列的前n 项和的公式是1(1)2n n n S na d -=+. （1）当1n =时，左边＝11S a =，右边＝111(11)12a d a ⨯-⨯+=，因此，左边＝右边. 所以，当1n =时命题成立.（2）假设当n k =时，命题成立，即1(1)2k k k S ka d -=+.那么，1111(1)[(1)1]2k k k k k S S a ka d a k d ++-=+=++++-1(1)(1)[1]2k k a k d -=+++1(1)(1)2k kk a d +=++所以，当1n k =+时，命题也成立.根据（1）和（2），可知命题对任何n N *∈都成立. 2、略.。

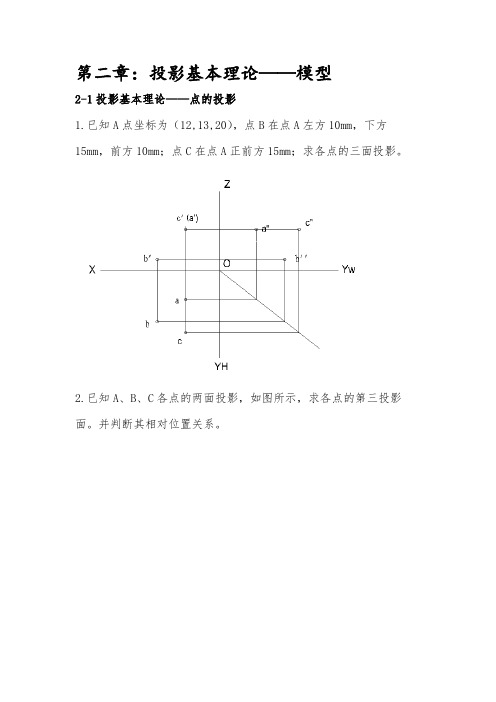
第二章：投影基本理论——模型
2-1投影基本理论——点的投影
1.已知A点坐标为（12,13,20），点B在点A左方10mm，下方15mm，前方10mm；点C在点A正前方15mm；求各点的三面投影。

2.已知A、B、C各点的两面投影，如图所示，求各点的第三投影面。

并判断其相对位置关系。

3.答案：
a’和a”不可见
4.答案：
2-2投影基本理论——直线的投影（一）
1.答案：
1.（1）正平；（2）侧平；（3）侧垂；（4）水平（5）正垂（6）一般位置直线
2.答案：
3.答案：
（1）正垂；（2）侧垂；（3）水平；（4）铅垂；
2-3投影基本理论——直线的投影（二）
1.答案
（1）平行；（2）交叉；（3）交叉；（4）相交；（5）相交；（6）平行；（7）交叉；
2-4投影基本理论——平面的投影
1.答案
（1）铅垂面；（2）水平面；（3）一般位置关系；（4）侧平面（5）侧垂面；（6）侧垂面；
2.答案
K不在，M不在，BN在
3.答案
无
2-5投影基本理论——综合
1.答案：
（1）正平;(2)正垂；（3）正平；
2.答案：
（1）一般位置;(2)正垂；（3）水平；
3.答案：
（1）正平；（2）下；（3）正平；
4.答案：
（1）正垂；（2）前；（3）侧垂；。

选修2-2微积分基本定理习题及答案一、选择题1．(2010·山东日照模考)a ＝⎠⎛02x d x ，b ＝⎠⎛02e x d x ，c ＝⎠⎛02sin x d x ，则a 、b 、c 的大小关系是( )A ．a <c <bB ．a <b <cC ．c <b <aD ．c <a <b[答案] D[解析] a ＝⎠⎛02x d x ＝12x 2|02＝2，b ＝⎠⎛02e x d x ＝e x |02＝e 2－1>2，c ＝⎠⎛02sin x d x ＝－cos x |02＝1－cos2∈(1,2)，∴c <a <b .2．(2010·山东理，7)由曲线y ＝x 2，y ＝x 3围成的封闭图形面积为( ) A.112 B.14C.13D.712[答案] A[解析] 由⎩⎪⎨⎪⎧y ＝x 2y ＝x 3得交点为(0,0)，(1,1)．∴S ＝⎠⎛01(x 2－x 3)d x ＝⎪⎪⎝⎛⎭⎫13x 3－14x 401＝112. [点评] 图形是由两条曲线围成的时，其面积是上方曲线对应函数表达式减去下方曲线对应函数表达式的积分，请再做下题：(2010·湖南师大附中)设点P 在曲线y ＝x 2上从原点到A (2,4)移动，如果把由直线OP ，直线y ＝x 2及直线x ＝2所围成的面积分别记作S 1，S 2.如图所示，当S 1＝S 2时，点P 的坐标是( )A.⎝⎛⎭⎫43，169B.⎝⎛⎭⎫45，169 C.⎝⎛⎭⎫43，157D.⎝⎛⎭⎫45，137[答案] A[解析] 设P (t ，t 2)(0≤t ≤2)，则直线OP ：y ＝tx ，∴S 1＝⎠⎛0t(tx －x 2)d x ＝t 36；S 2＝⎠⎛t2(x 2－tx )d x ＝83－2t ＋t 36，若S 1＝S 2，则t ＝43，∴P ⎝⎛⎭⎫43，169. 3．由三条直线x ＝0、x ＝2、y ＝0和曲线y ＝x 3所围成的图形的面积为( ) A ．4B.43C.185D ．6[答案] A[解析] S ＝⎠⎛02x 3d x ＝⎪⎪x 4402＝4.4．(2010·湖南省考试院调研)⎠⎛1－1(sin x ＋1)d x 的值为( )A ．0B ．2C ．2＋2cos1D ．2－2cos1[答案] B[解析] ⎠⎛1－1(sin x ＋1)d x ＝(－cos x ＋x )|－11＝(－cos1＋1)－(－cos(－1)－1)＝2.5．曲线y ＝cos x (0≤x ≤2π)与直线y ＝1所围成的图形面积是( ) A ．2π B ．3π C.3π2D ．π[答案] A[解析] 如右图， S ＝∫02π(1－cos x )d x ＝(x －sin x )|02π＝2π.[点评] 此题可利用余弦函数的对称性①②③④面积相等解决，但若把积分区间改为⎝⎛⎭⎫π6，π，则对称性就无能为力了． 6．函数F (x )＝⎠⎛0x t (t －4)d t 在[－1,5]上( )A ．有最大值0，无最小值B ．有最大值0和最小值－323C ．有最小值－323，无最大值D ．既无最大值也无最小值 [答案] B[解析] F ′(x )＝x (x －4)，令F ′(x )＝0，得x 1＝0，x 2＝4， ∵F (－1)＝－73，F (0)＝0，F (4)＝－323，F (5)＝－253.∴最大值为0，最小值为－323.[点评] 一般地，F (x )＝⎠⎛0x φ(t )d t 的导数F ′(x )＝φ(x )．7．已知等差数列{a n }的前n 项和S n ＝2n 2＋n ，函数f (x )＝⎠⎛1x 1td t ，若f (x )<a 3，则x 的取值范围是( )A.⎝⎛⎭⎫36，＋∞ B ．(0，e 21) C ．(e －11，e )D ．(0，e 11)[答案] D[解析] f (x )＝⎠⎛1x 1td t ＝ln t |1x ＝ln x ，a 3＝S 3－S 2＝21－10＝11，由ln x <11得，0<x <e 11.8．(2010·福建厦门一中)如图所示，在一个长为π，宽为2的矩形OABC 内，曲线y ＝sin x (0≤x ≤π)与x 轴围成如图所示的阴影部分，向矩形OABC 内随机投一点(该点落在矩形OABC 内任何一点是等可能的)，则所投的点落在阴影部分的概率是( )A.1πB.2πC.3πD.π4[答案] A[解析] 由图可知阴影部分是曲边图形，考虑用定积分求出其面积．由题意得S ＝⎠⎛0πsin x d x ＝－cos x |0π＝－(cosπ－cos0)＝2，再根据几何概型的算法易知所求概率P ＝S S 矩形OABC＝22π＝1π. 9．(2010·吉林质检)函数f (x )＝⎩⎪⎨⎪⎧x ＋2(－2≤x <0)2cos x (0≤x ≤π2)的图象与x 轴所围成的图形面积S 为( )A.32B ．1C ．4D.12[答案] C[解析] 面积S ＝∫π2－2f (x )d x ＝⎠⎛0－2(x ＋2)d x ＋∫π202cos x d x ＝2＋2＝4.10．(2010·沈阳二十中)设函数f (x )＝x －[x ]，其中[x ]表示不超过x 的最大整数，如[－1.2]＝－2，[1.2]＝1，[1]＝1.又函数g (x )＝－x3，f (x )在区间(0,2)上零点的个数记为m ，f (x )与g (x )的图象交点的个数记为n ，则⎠⎛mn g (x )d x 的值是( )A ．－52B ．－43C ．－54D ．－76[答案] A[解析] 由题意可得，当0<x <1时，[x ]＝0，f (x )＝x ，当1≤x <2时，[x ]＝1，f (x )＝x －1，所以当x ∈(0,2)时，函数f (x )有一个零点，由函数f (x )与g (x )的图象可知两个函数有4个交点，所以m ＝1，n ＝4，则⎠⎛m ng (x )d x ＝⎠⎛14⎝⎛⎭⎫－x 3d x ＝⎪⎪－x 2614＝－52. 11．(2010·江苏盐城调研)甲、乙两人进行一项游戏比赛，比赛规则如下：甲从区间[0,1]上随机等可能地抽取一个实数记为b ，乙从区间[0,1]上随机等可能地抽取一个实数记为c (b 、c 可以相等)，若关于x 的方程x 2＋2bx ＋c ＝0有实根，则甲获胜，否则乙获胜，则在一场比赛中甲获胜的概率为( )A.13B.23C.12D.34[答案] A[解析] 方程x 2＋2bx ＋c ＝0有实根的充要条件为Δ＝4b 2－4c ≥0，即b 2≥c ， 由题意知，每场比赛中甲获胜的概率为p ＝⎠⎛01b 2db 1×1＝13.12．(2010·吉林省调研)已知正方形四个顶点分别为O (0,0)，A (1,0)，B (1,1)，C (0,1)，曲线y ＝x 2(x ≥0)与x 轴，直线x ＝1构成区域M ，现将一个质点随机地投入正方形中，则质点落在区域M 内的概率是( )A.12B.14C.13D.25[答案] C[解析] 如图，正方形面积1，区域M 的面积为S ＝⎠⎛01x 2d x＝13x 3|01＝13，故所求概率p ＝13. 二、填空题13．(2010·芜湖十二中)已知函数f (x )＝3x 2＋2x ＋1，若⎠⎛1－1f (x )d x ＝2f (a )成立，则a ＝________.[答案] －1或13[解析] ∵⎠⎛1－1f (x )d x ＝⎠⎛1－1(3x 2＋2x ＋1)d x ＝(x 3＋x 2＋x )|－11＝4，⎠⎛1－1f (x )d x ＝2f (a )，∴6a 2＋4a ＋2＝4，∴a ＝－1或13.14．已知a ＝∫π20(sin x ＋cos x )d x ，则二项式(a x －1x )6的展开式中含x 2项的系数是________．[答案] －192[解析] 由已知得a ＝∫π20(sin x ＋cos x )d x ＝(－cos x ＋sin x )|π20＝(sin π2－cos π2)－(sin0－cos0)＝2，(2x －1x)6的展开式中第r ＋1项是T r ＋1＝(－1)r ×C 6r ×26－r ×x 3－r ，令3－r ＝2得，r ＝1，故其系数为(－1)1×C 61×25＝－192.15．抛物线y 2＝2x 与直线y ＝4－x 围成的平面图形的面积为________． [答案] 18[解析] 由方程组⎩⎪⎨⎪⎧y 2＝2x y ＝4－x 解得两交点A (2,2)、B (8，－4)，选y 作为积分变量x ＝y 22、x ＝4－y∴S ＝⎠⎛2－4[(4－y )－y 22]dy ＝(4y －y 22－y 36)|－42＝18.16．(2010·安徽合肥质检)抛物线y 2＝ax (a >0)与直线x ＝1围成的封闭图形的面积为43，若直线l 与抛物线相切且平行于直线2x －y ＋6＝0，则l 的方程为______．[答案] 16x －8y ＋1＝0[解析] 由题意知⎠⎛01ax d x ＝23，∴a ＝1，设l ：y ＝2x ＋b 代入y 2＝x 中，消去y 得， 4x 2＋(4b －1)x ＋b 2＝0， 由Δ＝0得，b ＝18，∴l 方程为16x －8y ＋1＝0.17．(2010·福建福州市)已知函数f (x )＝－x 3＋ax 2＋bx (a ，b ∈R )的图象如图所示，它与x 轴在原点处相切，且x 轴与函数图象所围成区域(图中阴影部分)的面积为112，则a 的值为________．[答案] －1[解析] f ′(x )＝－3x 2＋2ax ＋b ，∵f ′(0)＝0，∴b ＝0，∴f (x )＝－x 3＋ax 2，令f (x )＝0，得x ＝0或x ＝a (a <0)．S 阴影＝－⎠⎛a0(－x 3＋ax 2)d x ＝112a 4＝112，∴a ＝－1.三、解答题18．如图所示，在区间[0,1]上给定曲线y ＝x 2，试在此区间内确定t 的值，使图中阴影部分的面积S 1＋S 2最小．[解析] 由题意得S 1＝t ·t 2－⎠⎛0t x 2d x ＝23t 3，S 2＝⎠⎛t1x 2d x －t 2(1－t )＝23t 3－t 2＋13，所以S ＝S 1＋S 2＝43t 3－t 2＋13(0≤t ≤1)．又S ′(t )＝4t 2－2t ＝4t ⎝⎛⎭⎫t －12， 令S ′(t )＝0，得t ＝12或t ＝0.因为当0<t <12时，S ′(t )<0；当12<t ≤1时，S ′(t )>0.所以S (t )在区间⎣⎡⎦⎤0，12上单调递减，在区间⎣⎡⎦⎤12，1上单调递增． 所以，当t ＝12时，S min ＝14.。

安全用电习题册答案第一章触电与触电防护§1-1 电气事故基本知识一、填空题1.发电、输电、变电、配电、用电2.技术工人、工程技术人员、生产管理人员3. 规律性4. 安全操作规程二、选择题1.B2.D3.C4.A5.C6.C三、判断题1.√2.×3.√4.√5.√6.×7.√8.√9.√ 10.√ 11.√§1-2 触电方式一、填空题1.生理、病理2.电灼伤、电烙印、皮肤金属化3.感知电流、摆脱电流、致命电流4.直接电击、间接电击5. 电标、电纹、电流斑6.内部电阻、皮肤电阻7.42V、36V、24V、12V、6V8. 单相触电、两相触电、跨步电压触电二、选择题1.D2.C3.A4.C5.A6.D7.C8.A9.A 10.D 11.C 12.B三、判断题1.×2.√3.×4.×5.√6.×7.×8.√9.√ 10.× 11.ק1-3 触电急救一、填空题1. 抢救迅速、救护得法2. 拉闸断电3.人工呼吸、胸外心脏挤压4.冷水浇淋、猛烈摇晃、大声呼喊、架着触电者跑步5.绝缘手套、绝缘靴二、选择题1.C2.C3.A4.D三、判断题1.×2.√3.√4.√5.×6.ק1-4 外伤救护一、填空题1. 工具、绝缘工具、牢固的绳索2. 伤员的反应、呼吸、循环3. 无菌生理盐水、酒精、消毒被单或干净布片二、选择题1.C2.B三、判断题1.×2.√3.√4.√第二章安全防护技术及应用§2-1 屏护、间距及安全距离一、填空题1.安全第一、预防为主、安全防护技术2.电击、短路、故障接地3. 危险的带电体、外界、永久性屏护装置、临时性屏护装置、固定屏护装置、移动屏护装置4.带电体与地面之间、带电体与其他设备和设施之间、带电体与带电体之间5.7m、6m、3m、1.5m6. 隔热处理7. 动力、照明8. 禁止、停止；警告、注意；指令；通行、安全和提示信息9. 安全标志10. 禁止标志、警告标志、指令标志、提示标志11. 指令标志12. 文字、图形、安全色；禁止类、允许类、警告类二、选择题1.A2. C3.A4.B5.A6.C7.C8.B9.D 10.A11.B 12.D A 13.A C 14.C 15.C三、判断题1.×2.×3.√4.×5.×6.√7.×8.×9.× 10.√§2-2 绝缘防护一、填空题1. 气体绝缘、液体绝缘、固体绝缘、固体绝缘2. 电气性能、机械性能、热性能、吸潮性能、化学稳定性、抗生物性、电气性能、耐热性3. 导气性能、介电性能、绝缘强度4.Y、A、E、B、F、H、C5.低压绝缘子、高压绝缘子6. 绝缘的破坏、漏电、短路二、选择题1.C2.B3.C4.D5.A6.A7.A8.D三、判断题1.√2.√3.×4.×5.×6.×7.×8.√9.× 10.ק2-3 保护接地一、填空题1. 大地2. 工作接地、保护接地、重复接地、防雷接地3. 接地线、接地体、大地二、选择题1.A2.B3.A4.A5.A6.A7.B三、判断题1.×2.√3.√4.×5.×6.√7.×8.ק2-4 保护接零一、填空题1. 金属部分、配电网的中性点2.TN-S、TN-C-S、TN-C3. 零线、工作接地、其他点4. 保护接零二、选择题1.B2.C3.A4.A5.C6.A7.C三、判断题1.×2.√3.×4.×5.×6.√7.×8.√9.√ 10.× 11.ק2-5 接地装置一、填空题1. 接地体、接地线、自然接地体、人工接地体2. 用于其他目的，且与土壤保持紧密接触3. 钢管、角钢、圆钢、废钢铁、导体、垂直接地体、水平接地体4. 接地电阻5．五二、选择题1.D2.C3.A4.A5.C6.B三、判断题1.×2.×3.×4.×5.×6.√7.√§2-6 漏电保护装置一、填空题1. 漏电保护2. 额定电压、额定电流、分断能力3. 电压、电流、脉冲；漏电继电器、漏电开关、漏电保护插座4. 直接动作式、间接动作式；直接动作式、间接动作式5. 电磁、电子二、选择题1.A2.C3.B4.D5.C6.A7.C8.B9.A 10.B 11.C 12.C三、判断题1.×2.√3.×4.√5.×6.×7.×8.×9.× 10.ק2-7 过电压及其防护一、填空题1. 突然升高、大气过电压、内部过电压2. 雷击防护、直接雷击、感应雷击3. 接闪器、引下线、接地装置、接闪器、避雷针、线、网、带4. 操作过电压、谐振过电压、弧光接地过电压、2.75～45. 击穿保险器、过电压保护器（TBP）二、选择题1.B2.A3.D4.C5.D6.B7.B8.B9.C 10.B 11.A三、判断题1.×2.×3.√4.√5.√6.√7.√8.×9.√ 10.√§2-8 电气防火与防爆一、填空题1.防火、灭火、“预防为主，防消结合”、“以防为主，以消为辅”2.火警3.过载4. H-1、H-2、H-3，Q-1、Q-2、Q-3，G-1、G-25.过载，短路、电弧和火花，接触不良，烘烤，摩擦6. 切断电源、灭火7. 断路器、电磁起动器8. 喷头、阀门、报警控制装置和管道附件、湿式系统、干式系统、预作用系统、雨淋系统、水喷雾系统、水幕系统9. 其他设备、易燃物品、电源开关、热继电器二、选择题1.A2.C3.C4.C5.A6.B7.B三、判断题1.√2.√3.×4.×5.√6.×7.√8.ק2-9 静电防护一、填空题1. 带电、正电荷、负电荷2. 接地、屏蔽、增湿、加抗静电添加剂、静电中和法、工艺控制法3. 静电消除器、电子、离子、感应式、高压式、放射线式二、选择题1.A2.B3.B4.B5.D三、判断题1.×2.×3.×4.×5.×6.√第三章电气设备及线路的安全运行§3-1 变配电设备的运行和故障处理一、填空题1.经济传输、灵活分配、安全使用2.压力释放器3.变电、电能计量、无功补偿、动力配电、照明配电4.高压电源、负荷电流、短路电流5.输送、变换、分配、控制、指示、监测、保护6.负荷侧、电源侧、电源侧、负荷侧7.绝缘手套、合格的绝缘杆、绝缘杆8.操作、监护9. 0.7m、1m二、选择题1.D2.A3.B4.B5.A6.D三、判断题1.×2.√3.×4.√5.√6.√7.×8.×9.√ 10.×11.√ 12.× 13.√ 14.ק3-2 电气线路的安全技术一、填空题1.巡视检查2.计算负荷3. 电压、电流、容量、温度4. 工作、超过5.导线的安全载流量、线芯6. 防水弯、200mm二、选择题1.D2.B3.B4.A5.C6.D三、判断题1.√2.×3.√4.√5.√6.√7.√8.√9. × 10.√11.√ 12.√ 13.× 14.√§3-3 用电设备的安全技术一、填空题1.过载、短路、断相、失压2. 1～1.253.相线、零线4. 2.5、25. 电源开关、拔下电源插头6. 焊接电缆、接地、接地或接零7.一相一地、三相星形二、选择题1.A2.B3.C4.A5.D6.B7.C8.C9.B三、判断题1.×2.√3.×4.√5.√6.×7.√8.√9.√ 10.ק3-4 电气测试的安全技术一、填空题1.非破坏性试验、破坏性试验2. 绝缘试验、电气特性试验、机械特性试验3.断开电源、对地4. 接地电阻5. 最低、三、四、下雨6.工频大电流三极法、30A二、选择题1.B2.A3.B三、判断题1.×2.×3.×4.×5.√第四章电气安全工作制度§4-1 电工安全用具一、填空题1. 安全器具、电气工作安全用具、机械工作安全用具2. 绝缘、一般防护3. 万用表、兆欧表、钳形电流表4. 基本安全用具、辅助安全用具5. 电压、电流、电阻6. 高压隔离开关、跌落保险、临时接地线7.护目镜、绝缘手套、穿绝缘靴(鞋)、绝缘台(垫)、防雨绝缘夹钳8.普通靴、石油类油脂二、选择题1.A2.C3.D4.A5.B6.B7.B8.B9.C三、判断题1.×2.×3.×4.√5.√6.√7.√8.×9.√ 10.×11.× 12.√§4-2 电气值班制度一、填空题1. 《电业安全工作规程》、《运行规程》2. 事故处理、倒闸操作、交的细致、接的明白3. 轮班制、在家值班制、无人值班制、自动化、无人值班4. 总指挥者、业务知识、现场指挥经验、掌握5. 值班与巡视工作的直接执行者、监视和控制、合格的电力6. 负责人、值班调度员、值班人员7. 缺陷、异常现象、安全性二、选择题1.A2.C3.A4.D5.C三、判断题1.√2.√3.×4.√5.√6.√§4-3 电工安全技术操作规程一、填空题1.人、物（设备）2.作业、监护3.电源切断(拉断刀闸，取下保险)、“禁止合闸，有人工作”4.外壳接地线、工作零线5.双绕组型、自耦变压器、相线6.36V7.绝缘手套、接地线端、导线端、导线端、地线端二、选择题1.B2.C3.A4.D三、判断题1.√2.×3.×4.×5.√6.×7.√§4-4 电工安全作业制度一、填空题1. 电气设备、线路、全停电、部分停电、停电、验电、装挂接地线、悬挂标示牌和装设遮栏2. 隔离开关、断开点3. 两侧4. 火花、放电的“噼啪”声5. 低压、高压、下层、上层6. 低压设备、低压线路7. 干燥的绝缘垫、绝缘站台、其他绝缘物、绝缘柄、锉刀、金属尺、带有金属物的毛刷及毛掸二、选择题1.A2.A3.B4.A5.A6.B三、判断题1.√2.√3.×4.√5.√6.×7.√8.√§4-5 农村电工安全作业制度一、填空题1. 农村电工2.工作许可人3. 安全用电、安全用电、安全用电、节约用电、依法用电二、选择题1.B2.A3.A三、判断题1.√2.√3.√4.×第五章安全用电的监查和电气事故的处理§5-1 安全用电的检查制度一、填空题1. 安装、运行、维护、检修、管理工作2. 定期检查3. 用电重要性、设备情况、管理水平4.8m、4m、绝缘靴、绝缘手套二、选择题1.C2.C3.B4.C5.C6.B7.A三、判断题1.√2.×3.√4.√5.√6.√7.√8.×9.× 10.√§5-2 安全用电宣传和管理一、填空题1. 安全用电宣传、安全用电竞赛2. 电力部门、上级主管部门二、选择题1.C2.A三、判断题1.√2.√§5-3 用电事故的调查分析一、填空题1.事故原因、事故后果、事故责任2. 用户影响系统事故、用户全厂停电事故、用户主要电气设备损坏事故、用户人员触电死亡事故二、选择题1.B2.A三、判断题1.√2.×3.×4.√§5-4 用电事故的处理一、填空题1. 报当地电力部门的用电监察机构、报用户主管部门、用户存查2. 专业技术人员、动态、发展趋势、规律和特点、防范措施、反事故对策二、判断题1.√2.√。

基础课程教学资料第二章习题2-1 图2-1所示的电路中，U S=1V，R1=1Ω，I S=2A.，电阻R消耗的功率为2W。

试求R的阻值。

2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。

图中I S=2A，U S=2V，R1=3Ω，R2=R3=2Ω。

2-3 试用叠加原理重解题2-2.2-4再用戴维宁定理求题2-2中I3。

2-5 图2-3所示电路中,已知U S1=6V，R1=2Ω，I S=5A，U S2=5V，R2=1Ω，求电流I。

2-6 图2-4所示电路中，U S1=30V，U S2=10V，U S3=20V，R1=5kΩ，R2=2kΩ，R3=10kΩ，I S=5mA。

求开关S在位置1和位置2两种情况下，电流I分别为多少？2-7 图2-5所示电路中，已知U AB=0，试用叠加原理求U S的值。

2-8 电路如图2-6所示，试用叠加原理求电流I。

2-9 电路如图2-7所示，试用叠加原理求电阻R4上电压U的表达式。

2-10电路如图2-8所示,已知R1=Ω，R2=R3=2Ω，U S=1V，欲使I=0，试用叠加原理确定电流源I S的值。

2-11 画出图2-9所示电路的戴维宁等效电路。

2-12 图2-10所示的电路接线性负载时，U 的最大值和I的最大值分别是多少？2-13 电路如图2-11所示，假定电压表的内阻无穷大，电流表的内阻为零。

当开关S处于位置1时，电压表的读数为10V，当S处于位置2时，电流表的读数为5mA。

试问当S处于位置3SHI 4，电压表和电流表的读数各为多少？2-14 图2-12所示电路中，各电源的大小和方向均未知，只知每个电阻均为6Ω，又知当R=6Ω时，电流I=5A。

今欲使R支路电流I=3A，则R应该多大？2-15 图2-13所示电路中，N为线性有源二端网络，测得AB之间电压为9V，见图（a）；若连接如图（b）所示，可测得电流I=1A。

现连接如图（c）所示形式，问电流I为多少？2-16 电路如图2-14所示，已知R1=5Ω时获得的功率最大，试问电阻R是多大？本章小结1、支路电流法是分析和计算电路的基本方法，适用于任何电路。

习题2-1图 习题2-2图习题2-3图 习题2-4图习题2-5图 习题2-6图材料力学习题大全及答案第1章 引 论1－1 图示矩形截面直杆，右端固定，左端在杆的对称平面内作用有集中力偶，数值为M 。

关于固定端处横截面A －A 上的内力分布，有四种答案，根据弹性体的特点，试分析哪一种答案比较合理。

正确答案是 C 。

1－2 图示带缺口的直杆在两端承受拉力F P 作用。

关于A －A 截面上的内力分布，有四种答案，根据弹性体的特点，试判断哪一种答案是合理的。

正确答案是 D 。

1－3 图示直杆ACB 在两端A 、B 处固定。

关于其两端的约束力有四种答案。

试分析哪一种答案最合理。

正确答案是 D 。

1－4 等截面直杆在两端承受沿杆轴线的拉力F P 。

关于杆中点处截面A －A 在杆变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试判断哪一种答案是正确的。

正确答案是 D 。

1－5 图示等截面直杆在两端作用有力偶，数值为M ，力偶作用面与杆的对称面一致。

关于杆中点处截面A －A 在杆变形后的位置（对于左端，由A A '→；对于右端，由A A ''→），有四种答案，试判断哪一种答案是正确的。

正确答案是 C 。

习题2-1图习题2-2图习题2-3图习题2-4图1－6 等截面直杆，其支承和受力如图所示。

关于其轴线在变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试分析哪一种是合理的。

正确答案是 C 。

第2章 杆件的内力分析2－1 平衡微分方程中的正负号由哪些因素所确定？简支梁受力及Ox 坐标取向如图所示。

试分析下列平衡微分方程中哪一个是正确的。

（A ）d d Q x F d M（B ）d d Q x F （C ）d d Q x F （D ）d d Q xF 2－2 对于图示承受均布载荷q 的简支梁，其弯矩图凸凹性与哪些因素相关？试判断下列四种答案中哪几种是正确的。

第一单元变压器的分类、结构和原理；课题一变压器的分类和用途；一、填空题（每空1分）；1．变压器是一种能变换________电压，而_；答案：交流频率电磁感应；2．变压器的种类很多，按相数分为______ __；答案：单相三相；3．在电力系统中使用的电力变压器，可分为____；答案：升压降压配电；二、判断题（每题1分）；1．变压器的基本工作原理是电流的磁效应；答第一单元变压器的分类、结构和原理课题一变压器的分类和用途一、填空题（每空1分）1．变压器是一种能变换________电压，而___________不变的静止电气设备。

它是根据___________原理来变换电压以满足不同负载的需要。

答案：交流频率电磁感应2．变压器的种类很多，按相数分为________和_________变压器；答案：单相三相3．在电力系统中使用的电力变压器，可分为_________变压器、___ ______变压器和_________变压器。

答案：升压降压配电二、判断题（每题1分）1．变压器的基本工作原理是电流的磁效应。

（）答案：×2．在电路中所需的各种直流电，可以通过变压器来获得。

（）答案：×三、简答题（每题3分）1、为什么要高压送电？答案：当输出电功率一定时，电压越大，电流越小。

2（1）P损= IR，可以减少运输中的损耗。

（2）可以节约架设成本。

2、变压器能改变直流电压吗？如接上直流电压，会发生什么现象？答案：不能。

如果接上直流电压，会使绕组过热而烧毁。

课题二变压器的结构与冷却方式一、填空题（每空1分）1．变压器的铁心常用_________叠装而成，因线圈位置不同，可分成_________和_________两大类。

答案：硅钢片芯式壳式2．变压器的绕组常用绝缘铜线或铜箔绕制而成。

接电源的绕组称为____________；接负载的绕组称为___________。

也可按绕组所接电压高低分为___________和___________。