2023-2024学年人教版八年级数学上学期：课题学习 最短路径问题(附答案解析)

第十三章轴对称13. 4课题学习最短路径问题一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．A、B是直线l上的两点，P是直线l上的任意一点，要使PA+PB的值最小，那么点P的位置应在A．线段AB上B．线段AB的延长线上C．线段AB的反向延长线上D．直线l上【答案】A2．直线l是一条河，P，Q是两个村庄．欲在L上的某处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是lA．B．C．D．【答案】D【解析】本题的依据就是两点之间线段最短．首先作点P关于直线l的对称点P′，连接P′Q就是最短的路程．故选D．学&科网3．如图，在△ABC中，∠C=90°，∠BAC=30°，AB=8，AD平分∠BAC，点PQ分别是AB、AD边上的动点，则PQ+BQ的最小值是A．4 B．5C．6 D．7【答案】A二、填空题：请将答案填在题中横线上．4．已知，如图△ABC为等边三角形，高AH=10 cm，P为AH上一动点，D为AB的中点，则PD+PB的最小值为__________cm．【答案】10学&科网【解析】如图，连接PC，∵△ABC为等边三角形，D为AB的中点，∴CD⊥AB，∴CD=AH=10 cm．∵AH⊥BC，∴PB=PC，∴PD+PB的最小值为：PD+PB=PC+PD=CD=AH=10 cm．故答案为：10．学&科网5．如图，△ABC中，AC=10，AB=12，△ABC的面积为48，AD平分∠BAC，F，E分别为AC，AD上两动点，连接CE，EF，则CE+EF的最小值为__________．【答案】8三、解答题：解答应写出文字说明、证明过程或演算步骤．6．要在燃气管道L上修建一个泵站P，分别向A，B两镇供气，泵站修在管道的什么地方，可使所用的输气管线最短？在图上画出P 点位置，不写作法，保留痕迹．【解析】如图，作点A 关于燃气管道L 的对称点A ′，连接A ′B 交L 于点P ，即点P 即为所求．7．如图所示的方格纸中，每个小方格的边长都是1，点(41)A -，，(33)B -，，(12)C -，． （1）作ABC △关于y 轴对称的A'B'C'△；（2）在x 轴上找出点P ，使PA PC +最小，并直接写出点P 的坐标．。

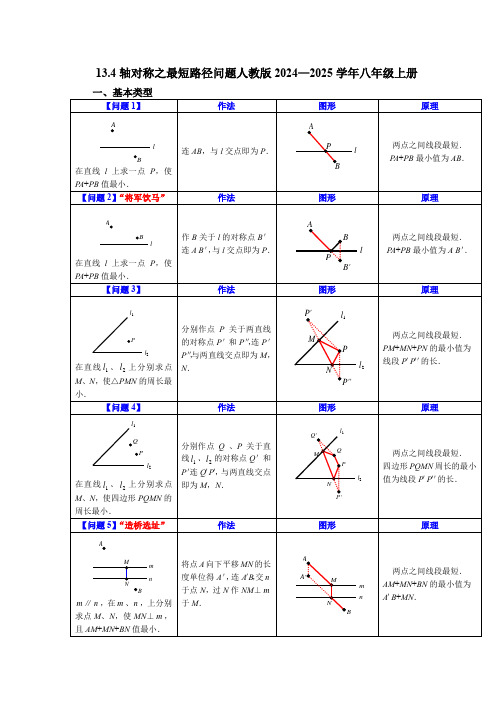
13.4轴对称之最短路径问题人教版2024—2025学年八年级上册二、例题讲解例1.如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC，已知线段AB＝4，DE＝2，BD＝8，设CD＝x．（1）用含x的代数式表示AC+CE的长；（2）请问点C满足什么条件时，AC+CE最小？最小为多少？（3）根据（2）中的规律和结论，请构图求代数式的最小值．变式1.如图，C为线段BD上一动点，分别过点B，D作AB⊥BD，ED⊥BD，连结AC，EC，已知AB＝5，DE＝1，BD＝8．（1）请问点C什么位置时AC+CE的值最小？最小值为多少？（2）设BC＝x，则AC+CE可表示为，请直接写出的最小值为．例2.如图，直线l是一条河，P，Q是两个村庄，欲在l上的某处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（）A．B．C．D．变式1.如图，在⊥ABC中，BA＝BC，BD平分⊥ABC，交AC于点D，点M、N 分别为BD、BC上的动点，若BC＝10，⊥ABC的面积为40，则CM+MN的最小值为．变式2.如图，等腰三角形ABC的底边BC长为8，面积是24，腰AC的垂直平分线EF分别交AC，AB于E，F点，若点D为BC边的中点，点M为线段EF 上一动点，则⊥CDM的周长的最小值为（）A．7B．8C．9D．10变式3.如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点．（1）点D的坐标为；（2）若E为边OA上的一个动点，当⊥CDE的周长最小时，求点E的坐标．例3.如图，⊥AOB内一点P，P1，P2分别是P关于OA、OB的对称点，P1P2交OA于点M，交OB于点N．若⊥PMN的周长是6cm，则P1P2的长为（）A．6cm B．5cm C．4cm D．3cm变式1.已知点P在⊥MON内．如图1，点P关于射线OM的对称点是G，点P 关于射线ON的对称点是H，连接OG、OH、OP．（1）若⊥MON＝50°，求⊥GOH的度数；（2）如图2，若OP＝6，当⊥P AB的周长最小值为6时，求⊥MON的度数．变式2.如图，⊥MON＝45°，P为⊥MON内一点，A为OM上一点，B为ON上一点，当⊥P AB的周长取最小值时，⊥APB的度数为（）A．45°B．90°C．100°D．135°变式3.如图，⊥AOB＝30°，P是⊥AOB内的一个定点，OP＝12cm，C，D分别是OA，OB上的动点，连接CP，DP，CD，则⊥CPD周长的最小值为．变式4.如图，在五边形中，⊥BAE＝140°，⊥B＝⊥E＝90°，在边BC，DE上分别找一点M，N，连接AM，AN，MN，则当⊥AMN的周长最小时，求⊥AMN+⊥ANM 的值是（）A．100°B．140°C．120°D．80°例4.如图，在⊥ABC中，AB＝AC，⊥A＝90°，点D，E是边AB上的两个定点，点M，N分别是边AC，BC上的两个动点．当四边形DEMN的周长最小时，⊥DNM+⊥EMN的大小是（）A．45°B．90°C．75°D．135°变式1.如图，在平面直角坐标系中，已知点A（0，1），B（4，0），C（m+2，2），D（m，2），当四边形ABCD的周长最小时，m的值是（）A．B．C．1D．变式2.如图，在四边形ABCD中，⊥B＝90°，AB⊥CD，BC＝3，DC＝4，点E 在BC上，且BE＝1，F，G为边AB上的两个动点，且FG＝1，则四边形DGFE 的周长的最小值为．例5.如图，⊥AOB＝20°，点M、N分别是边OA、OB上的定点，点P、Q分别是边OB、OA上的动点，记⊥MPQ＝α，⊥PQN＝β，当MP+PQ+QN最小时，则β﹣α的值为（）A．10°B．20°C．40°D．60°变式1.如图，∠AOB＝20°，M，N分别为OA，OB上的点，OM＝ON＝3，P，Q分别为OA，OB上的动点，求MQ+PQ+PN的最小值。

第05讲最短路径课程标准学习目标①最短路径的基本原理②最短路径的基本模型 1.掌握最短路径的基本原理，即两点之间线段最短，点到直线的距离最短。

2.掌握最短路径的几种模型，能够熟练的运用轴对称，垂直平分线的性质解决相应题目。

知识点01最短路径的基本原理1.最短路径的基本原理：①两点之间，线段最短。

如图，②号线最短②点到直线的距离最短。

如图，PC最短。

③垂直平分线上任意一点到线段两端点的距离相等。

如图，MN是垂直平分线，CA=CB。

知识点02最短路径的基本类型1——直线上一点到同侧两点的距离之和最短1.如图，存在直线l以及直线外的点P和点Q，直线l上存在一点M，使得MP＋MQ的值最小：方法点拨：作其中一点关于直线的对称点，连接对称点与另一点，线段与直线的交点即为要找的点M。

解：如图，作点P关于直线l的对称点p’。

连接P’Q，P’Q与直线l交于点M，则此时MP＋MQ最小。

证明：∵P与P’关于直线l对称∴直线l是PP’的垂直平分线∴MP＝MP’∴MP＋MQ＝MP’＋MQ＝P’Q。

∴MP＋MQ此时有最小值，为P’Q的长度题型考点：①基本作图。

②求值计算。

【即学即练1】1．如图，在正方形网格中有M，N两点，在直线l上求一点P使PM+PN最短，则点P应选在（）A．A点B．B点C．C点D．D点【解答】解：如图，点M′是点M关于直线l的对称点，连接M′N，则M′N与直线l的交点，即为点P，此时PM+PN最短，∵M′N与直线l交于点C，∴点P应选C点．故选：C．【即学即练2】2．如图，在等边△ABC中，BC边上的高AD＝6，E是高AD上的一个动点，F是边AB的中点，在点E运动的过程中，EB+EF存在最小值，则这个最小值是（）A．5B．6C．7D．8【解答】解：如图，连接CE，∵等边△ABC中，AD是BC边上的中线，∴AD是BC边上的高线，即AD垂直平分BC，∴EB＝EC，∴BE+EF＝CE+EF，∴当C、F、E三点共线时，EF+EC＝EF+BE＝CF，∵等边△ABC中，F是AB边的中点，∴AD＝CF＝6，即EF+BE的最小值为6．故选：B．知识点03最短路径基本类型——角内一点与角两边构成的三角形周长最短1.如图，已知∠MON 以及角内一点P ，角的两边OM 与ON 上存在点A 与点B ，使得△PAB 的周长最小：方法点拨：分别作点P 关于OM 与ON 的对称点P ’与P ’’，连接P ’P ’’。

课时目标1.能利用轴对称和平移解决简单的最短路径问题,培养学生从实际问题抽象出熟悉模型的能力,增强应用意识.2.体会图形的变换在解决最值问题中的作用,培养学生几何直观和模型观念.3.通过解决问题感悟转化思想,进一步获得数学活动的经验,增强数学的应用意识.学习重点1.利用轴对称将最短路径问题转化为“两点之间,线段最短”问题.2.利用轴对称和平移将造桥选址问题转化为“两点之间,线段最短”问题.学习难点最短路径问题的解决思路及证明方法.课时活动设计情境引入1.如图,连接A,B两点的所有线中,哪条最短?为什么?解:②最短,因为两点之间,线段最短.2.如图,点P是直线l外一点,点P与该直线l上各点连接的所有线段中,哪条最短?为什么?解:PC最短,因为垂线段最短.3.以前还学习过哪些有关线段大小的结论?解:三角形三边关系:两边之和大于第三边;斜边大于直角边.4.如图,如何做点A关于直线l的对称点?解:过点A作直线l的垂线,交直线l于点O,延长AO到点A',使AO=A'O.设计意图:通过四个问题的设计回顾,为解决最短路径问题提供理论依据,培养学生运用定理的意识和在实际问题中发现数学问题的能力,培养学生的几何直观和空间观念.新知探究利用轴对称解决最短路径问题探究1“饮马问题”.问题:如图,牧马人从A地出发,到一条笔直的河流l边饮马,然后到B地,牧马人到河边的什么地方饮马,可使所走的路径最短?分析:即把A,B两地抽象为两点,将河流l抽象成为一条直线,在直线l上找一点C,使AC+BC最短.学生讨论并回答,师生共同总结得出,可以转化为两点在直线异侧的问题.追问1:能否通过图形变换(轴对称和平移)将点B“移”到l的另一侧B'处,满足直线l上的任意一点C,都保持CB与CB'的长度相等?作法:(1)作点B关于直线l的对称点B';(2)连接AB',与直线l相交于点C.则点C即为所求.追问2:如何证明这条路径最短?证明:如图,在直线l上任取一点C'(与点C不重合),连接AC',BC',B'C'.由轴对称的性质知,BC=B'C,BC'=B'C'.∴AC+BC=AC+B'C=AB',AC'+BC'=AC'+B'C'.在△AB'C'中,AB'<AC'+B'C',∴AC+BC<AC'+BC'.即AC+BC最短.探究2“造桥选址问题”.问题:如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,桥建在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直.)分析:把河的两岸看成两条平行线a和b,N为直线b上的一个动点,MN垂直于直线b,交直线a于点M,把问题转化为:当点N在直线b的什么位置时,AM+MN+NB最小.学生讨论并回答,师生共同归纳.追问1:能否通过将AM沿着与河岸垂直的方向平移,点M移动到点N,点A移动到点A',使A'N+NB最小?作法:(1)将AM沿着与河岸垂直的方向平移,点M移动到点N,点A移动到点A';(2)连接A'B ,点N 即为所求.追问2:如何证明点N 即为所求?小组合作交流,教师找学生展示答案.分析:如图,在直线b 上任意取一点N',过点N'作N'M'垂直于a ,垂足为M',连接AM',A'N',N'B.同“饮马问题”可证,AM +MN +AM'<AM'+A'N'+N'B.解:如图,在路径A →M →N →B 的左侧和右侧各任意作一条路径,即A →M 1→N 1→B 和A →M 2→N 2→B ,AM +MN +NB =BC +AC ,则AM 1+M 1N 1+N 1B =N 1C +N 1B +AC >BC +AC ,AM 2+M 2N 2+N 2B =N 2C +N 2B +AC >BC +AC.所以A →M →N →B 是最短路径.设计意图:通过问题层层递进,培养学生分析问题和解决问题的能力;培养学生用数学眼光看世界的能力,和用文字语言、图形语言、符号语言三种语言表达问题的能力以及三种语言的相互转化能力,培养学生严密的数学思维和严谨的科学态度.典例精讲例1(1)如图1,在AB 直线一侧C ,D 两点,在AB 上找一点P ,使C ,D ,P 三点组成的三角形的周长最短.说明理由.(2)如图2,在∠AOB 内部有一点P ,是否在OA ,OB 上分别存在点E ,F ,使得E ,F ,P 三点组成的三角形的周长最短,找出E ,F 两点.(3)如图3,在∠AOB 内部有两点M ,N ,是否在OA ,OB 上分别存在点E ,F ,使得E ,F ,M ,N ,四点组成的四边形的周长最短,找出E ,F 两点.解:(1)如图1,作C关于直线AB的对称点C',连接C'D交AB于点P.则点P就是所求作的点.理由如下:因为C和C'关于直线对称,所以PC=PC'.因为CD长度不变,所以DP+CP最短时,C,D,P三点组成的三角形的周长最短.因为两点之间线段最短,所以点P就是所求作的点.(2)如图2,作P关于OA的对称点P',关于OB的对称点P″,连接P'P″,交OA于点E,OB于点F,则点E,F就是所求作的点.(3)如图3,作M关于OA的对称点M',作N关于OB的对称点M″,连接M'M″,交OA于点E,OB于点F,则点E,F就是所求作的点.例2如图,荆州古城河在CC'处直角转弯,河宽相同,从A处到B处,须经两座桥DD',EE'(桥宽不计),设护城河以及两座桥都是东西、南北方向的,怎样架桥可使ADD',E'EB的路程最短?解:如图,将A点向F平移得到点F,B点向右平移得到点G.连接GF,与河岸相交于点E',D'.作DD',EE'即为桥.理由:由作图法可知,AF∥DD',AF=DD',则四边形AFD'D为平行四边形,于是AD=FD',同理,BE=GE',由两点之间线段最短可知,GF最小.设计意图:通过题目巩固所学知识,总结解决最短路径问题的方法:在解决最短路径问题时,我们通常利用轴对称、平移等变换把未知问题转化为已解决的问题,从而做出最短路径的选择.增强学生应用意识和创新能力.巩固训练1.如图,直线l是一条河,P、Q是两个村庄.欲在l上的某处修建一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需要管道最短的是(D)2.有两棵树位置如图,树的底部分别为A,B,地上有一只昆虫沿着A—B的路径在地面上爬行.小树顶D处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶C处.问小鸟飞至AB之间何处时,飞行距离最短,在图中画出该点的位置.解:如图所示.3.如图,A和B两地在一条河的两岸,现要在河上建一座桥MN.桥造在何处才能使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)解:如图所示.设计意图:通过练习,巩固所学知识,提高学生分析问题和解决问题的能力.课堂小结1.谈谈今天的收获.2.教师与学生一起回顾本节课所学的主要内容,并请学生回答以下问题:(1)本节课学习了哪些主要内容?(2)怎样解决最短路径问题?(3)本节课你学到了哪些研究问题的方法?设计意图:通过小结,使学生梳理本节课所学内容和研究方法,把握本节课的核心内容,引导学生从知识内容和学习过程两个方面总结自己的收获,掌握几何直观和模型观念,提升知识转化和迁移能力.课堂8分钟.1.教材第93页复习题13第15题.2.七彩作业.教学反思。

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！2023--2024学年度人教版数学八年级上册期末复习核心考点三种题型精炼专题10 最短路径问题1.如图，四边形ABCD中，∠BAD＝120°，∠B＝∠D＝90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN＋∠ANM的度数为 .【答案】120°【解析】考点有轴对称（最短路线问题），三角形三边关系，三角形外角性质，等腰三角形的性质。

根据要使△AMN的周长最小，即利用点的对称，让三角形的三边在同一直线上，作出A关于BC和ED的对称点A′，A″，即可得出∠AA′M＋∠A″＝∠HAA′＝60°，进而得出∠AMN＋∠ANM＝2(∠AA′M＋∠A″)即可得出答案：如图，作A关于BC和ED的对称点A′，A″，连接A′A″，交BC于M，交CD于N，则A′A″即为△AMN的周长最小值。

13.4课题学习：最短路径问题夯实基础篇一、单选题：1．直线L是一条河，P，Q是两个村庄．欲在L上的某处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（）．A．B．C．D．【答案】D【知识点】轴对称的应用-最短距离问题【解析】【解答】作点P关于直线L的对称点P′，连接QP′交直线L于M．根据两点之间，线段最短，可知选项D铺设的管道，则所需管道最短．故选D．【分析】利用对称的性质，通过等线段代换，将所求路线长转化为两定点之间的距离．2．如图，点M，N在直线l的同侧，小东同学想通过作图在直线l上确定一点Q，使MQ与QN的和最小，那么下面的操作正确的是（）A．B．C．D．【答案】C【知识点】轴对称的应用-最短距离问题【解析】【解答】作点M关于直线l的对称点M′，再连接M′N交l于点Q，则MQ+NQ=M′Q+NQ=M′N，由“两点之间，线段最短”，可知点Q即为所求.故答案为：C【分析】先作点M关于l的对称点M′，连接M′N交l于点Q，即可.3．如图，在等腰△AB C中，AB=AC=6，∠ACB=75°，AD⊥BC于D，点M、N分别是线段AB，AD上的动点，则MN+BN的最小值是（）C．4.5D．6A．3B．【答案】A【知识点】角平分线的性质；等腰三角形的性质；含30°角的直角三角形；轴对称的应用-最短距离问题【解析】【解答】解：如图，作BH⊥AC，垂足为H，交AD于M′点，过M′点作M′N′⊥AB，垂足为N′，则BM′+M′N′为所求的最小值．∵AB=AC，AD⊥BC于D，∴∠ABC=∠C，AD是∠BAC 的平分线，∴M′H=M′N′，∴BH是点B到直线AC的最短距离（垂线段最短），∵∠ABC=∠C，∠ACB=75°，∴∠BAC=30°，∵BH⊥AC，∴BH=12AB=3．故答案为：A【分析】根据等腰三角形的三线合一，得到AD是∠BAC的平分线，由角平分线的性质可知，角平分线上的点到角两边的距离相等，得到BH是点B到直线AC的最短距离，再由三角形内角和定理得到∠BAC=30°，根据在直角三角形中，30度角所对的边是斜边的一半，求出MN+BN的最小值.4．如图：△AB C中， ACB=90°，AC=BC，AB=4，点E在BC上，且BE=2，点P在 ABC 的平分线BD上运动，则PE+PC的长度最小值为（）A．1B．2C．3D．4【答案】B【知识点】三角形的角平分线、中线和高；轴对称的应用-最短距离问题【解析】【解答】作点E关于BD的对称点E'，连接E'C，如下图：∵BD是∠ABC的平分线，∴通过作图知，BP垂直平分EE'，∴PE'=PE∴此时PE+PC=PE'+PC=E'C，PE+PC的长度最小，∵点E、点E'关于BD的对称，∴BE'=BE=2，又∵AB=4，∴点E'是A B中点，CE'是中线.∵△AB C中，∠ACB=90°，AC=BC，∴△ABC是等腰直角三角形，∠ABC=45 ，∴CE'又是底边AB的高，∴△BE'C也是等腰直角三角形，∴E'C=2，即：PE+PC的长度最小值为2.故选B.【分析】此题考查最短路径问题，利用轴对称，作点E关于BD的对称点E'，连接E'C，可知此时PE+PC的长度最小，PE+PC=PE'+PC=E'C.再根据作图和等腰直角三角形性质求出E'C的长即可.5．如图，在锐角△AB C中，AB＝AC＝10，S△ABC＝25，∠BAC的平分线交BC于点D，点M，N分别是AD和AB上的动点，则BM＋MN的最小值是（）A．4B．245C．5D．6【答案】C【知识点】等腰三角形的性质；轴对称的应用-最短距离问题【解析】【解答】解：如图，∵AD 是∠BAC 的平分线，AB =AC ，∴点B 关于AD 的对称点为点C ，过点C 作CN ⊥AB 于N 交AD 于M ，由轴对称确定最短路线问题，点M 即为使BM ＋MN 最小的点，CN ＝BM ＋MN ，∵AB ＝10，S △ABC ＝25，∴12×10•CN ＝25，解得CN ＝5，即BM ＋MN 的最小值是5.故答案为：C.【分析】根据AD 是∠BAC 的平分线，AB =AC 可得出确定出点B 关于AD 的对称点为点C ，根据垂线段最短，过点C 作CN ⊥AB 于N 交AD 于M ，根据轴对称确定最短路线问题，点M 即为使BM ＋MN 最小的点，CN ＝BM ＋MN ，利用三角形的面积求出CN ，从而得解.6．如图，等边ABC 中，D 为A C 中点，点P 、Q 分别为AB 、AD 上的点，4BP AQ ，3QD ，在BD 上有一动点E ，则PE QE 的最小值为（）A ．7B ．8C ．10D ．12【答案】C【知识点】等边三角形的判定与性质；轴对称的应用-最短距离问题【解析】【解答】解：如图，ABC ∵是等边三角形，BA BC ，∵D 为A C 中点，∴BD AC ，∵4AQ ，3QD ，7AD DC AQ QD ，作点Q 关于BD 的对称点Q '，连接PQ '交BD 于E ，连接QE ，此时PE +QE 的值最小，最小值PE +QE =PE +EQ '=PQ '，4AQ ∵，7AD DC ，3QD DQ ，4CQ BP ，10AP AQ ，60A ∵，APQ 是等边三角形，10PQ PA ，∴PE +QE 的最小值为10.故答案为：C.【分析】作点Q关于BD的对称点Q'，连接PQ'交BD于E，连接QE，此时PE+QE 的值最小，最小值PE+QE=PE+EQ'=PQ'，进而判断△APQ'是等边三角形，即可解决问题.7．如图，等腰三角形ABC的底边BC长为3，面积是18，腰AC的垂直平分线EF分别交AC，AB边于E，F点.若点D为BC边的中点，点M为线段EF上一动点，则△CDM 周长的最小值为（）A．7.5B．8.5C．10.5D．13.5【答案】D【知识点】三角形的面积；线段垂直平分线的性质；等腰三角形的性质；轴对称的应用-最短距离问题【解析】【解答】解：如图，连接AM、AD∵EF垂直平分线段AC∴CM=AM∴CM+MD=AM+MD≥AD即当A、M、D三点在一直线上且与AD重合时，CM+MD取得最小值，且最小值为线段AD的长∵△CMD的周长=CM+MD+CD=AM+MD+AD∴△CMD的周长的最小值为AD+CD ∵D为BC的中点，AB=AC∴1 1.52CD BC，AD⊥BC∴13182ABCS AD∴AD=12∴AD+CD=12+1.5=13.5即△CDM周长的最小值为13.5故答案为：D.【分析】连接AM、AD，由线段垂直平分线的性质可得CM=AM，当A、M、D三点在一直线上且与AD重合时，CM+MD取得最小值，且最小值为线段AD的长；根据等腰三角形三线合一的性质可得1 1.52CD BC，AD⊥BC，利用△ABC的面积可求出AD的长，从而求出此时△CDM的周长即可.二、填空题：8．如图的4×4的正方形网格中，有A，B，C，D四点，直线a上求一点P，使PA+PB 最短，则点P应选点（C或D）.【答案】C【知识点】轴对称的应用-最短距离问题【解析】【解答】解：如图，点A ′是点A 关于直线a 的对称点，连接A ′B ，则A ′B 与直线a 的交点，即为点P ，此时PA +PB 最短，∵A ′B 与直线a 交于点C ，∴点P 应选C 点.故答案为：C.【分析】点A ′是点A 关于直线a 的对称点，连接A ′B ，则A ′B 与直线a 的交点，即为点P ，此时PA +PB 最短，据此即得结论.9．如图，在ABC 中，3,4,,AB AC AB AC EF 垂直平分BC ，点P 为直线EF 上一动点，则ABP 周长的最小值是．【答案】7【知识点】轴对称的应用-最短距离问题【解析】【解答】解：∵EF 垂直平分BC ，∴B ，C 关于直线EF 对称．设AC 交EF 于点D ，∴当P 和D 重合时，AP BP 的值最小，最小值等于AC 的长，∴ABP 周长的最小值是437 ．【分析】根据题意知点B关于直线EF的对称点为点C，故当点P与点D重合时，AP+BP 的最小值，求出AC长度即可得到结论．中，AB=4，AC=6，BC=7，EF垂直平分BC，点P为直线EF上10．如图，在ABC的任一点，则ABP周长的最小值是.【答案】10【知识点】轴对称的应用-最短距离问题【解析】【解答】解：如图，连接PC，∵，4AB，AB PA PB PA PB的周长为4ABP要使ABP的周长最小，则需PA PB的值最小，∵垂直平分BC，EF，PC PBPA PB PA PC ，由两点之间线段最短可知，当点,,A P C 共线，即点P 在AC 边上时，PA PC 取得最小值，最小值为AC ，即PA PB 的最小值为6AC ，则ABP 周长的最小值是4610 .故答案为：10.【分析】如图，连接PC ，先把ABP 的周长表示出来为4+PA +PB ，接着根据垂直平分线性质得到PB =PC ，故只需PA +PC 最小△ABP 周长才最小，由两点之间线段最短得出P 点在AC 上时最小，此时PA +PC =AC =6，从而即可得出答案.11．如图，在△AB C 中，AB ＝AC ＝10，BC ＝12，AD ＝8，AD 是∠BAC 的平分线.若P ，Q 分别是AD 和AC 上的动点，则PC +PQ 的最小值是.【答案】9.6【知识点】三角形的面积；等腰三角形的性质；轴对称的应用-最短距离问题【解析】【解答】解：∵AB ＝AC ，AD 是∠BAC 的平分线，∴AD 垂直平分BC ，∴BP ＝CP .过点B 作BQ ⊥AC 于点Q ，BQ 交AD 于点P ，则此时PC +PQ 取最小值，最小值为BQ 的长，如图所示.∵S△ABC12BC•AD12AC•BQ，∴BQ12810BC ADAC9.6.故答案为：9.6.【分析】根据等腰三角形的三线合一得出AD垂直平分BC，根据垂直平分线上的点到线段两个端点的距离相等得出BP＝CP，过点B作BQ⊥AC于点Q，BQ交AD于点P，则此时PC+PQ取最小值，最小值为BQ的长，然后根据三角形的面积法，得出BC•AD =AC•BQ，根据等积式即可求出BQ的长.三、作图题：12．有一个养鱼专业户，在如图所示地形的两个池塘里养鱼，他每天早上要从住处P分别前往两个池塘投放鱼食，试问他怎样走才能以最短距离回到住地?(请用尺规作图，保留作图痕迹，不写做法)【答案】解：答图如图所示，该养鱼专业户若要以最短距离回到住地，则他所走路线是：，P M N P.或P N M P【知识点】轴对称的应用-最短距离问题【解析】【分析】分别作P点关于AB，AC的对称点，连接这两个对称点交AB于点M，交AC于点N，该养鱼专业户若要以最短距离回到住地，则他所走路线是：，或P N M P.P M N P13．如图，P和Q为△ABC边AB与AC上两点，在BC边上求作一点M， 使△PQM的周长最小。