当前位置：文档之家 › 数值分析第二章 插值法

数值分析第二章 插值法

  • 格式：ppt
  • 大小：3.21 MB
  • 文档页数：120

下载文档原格式

  / 120

合集下载

数值分析实验报告--实验2--插值法

数值分析实验报告--实验2--插值法

1 / 21数值分析实验二：插值法1 多项式插值的震荡现象1.1 问题描述考虑一个固定的区间上用插值逼近一个函数。

显然拉格朗日插值中使用的节点越多，插值多项式的次数就越高。

我们自然关心插值多项式的次数增加时， 是否也更加靠近被逼近的函数。

龙格（Runge ）给出一个例子是极著名并富有启发性的。

设区间[-1,1]上函数21()125f x x=+ (1)考虑区间[-1,1]的一个等距划分，分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为201()()125nn ii iL x l x x ==+∑(2)其中的(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。

实验要求：(1) 选择不断增大的分点数目n=2, 3 …. ，画出原函数f(x)及插值多项式函数()n L x 在[-1，1]上的图像，比较并分析实验结果。

(2) 选择其他的函数，例如定义在区间[-5，5]上的函数x x g xxx h arctan )(,1)(4=+=重复上述的实验看其结果如何。

(3) 区间[a,b]上切比雪夫点的定义为 (21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭(3)以121,,n x x x +为插值节点构造上述各函数的拉格朗日插值多项式，比较其结果,试分析2 / 21原因。

1.2 算法设计使用Matlab 函数进行实验, 在理解了插值法的基础上，根据拉格朗日插值多项式编写Matlab 脚本，其中把拉格朗日插值部分单独编写为f_lagrange.m 函数，方便调用。

1.3 实验结果1.3.1 f(x)在[-1,1]上的拉格朗日插值函数依次取n=2、3、4、5、6、7、10、15、20，画出原函数和拉格朗日插值函数的图像，如图1所示。

Matlab 脚本文件为Experiment2_1_1fx.m 。

可以看出，当n 较小时，拉格朗日多项式插值的函数图像随着次数n 的增加而更加接近于f(x)，即插值效果越来越好。

数值分析第五版第二章_插值法

数值分析第五版第二章_插值法


于是
Ak
1
(x
j 0 j k
n
k
xj)
代入上式,得
(x x
l k ( x)
j 0 j k n
n
j
)
j 0 jk n
x xj xk x j
(x
j 0 j k
k
xj)
称
l k ( x) 为关于基点
x i 的n次插值基函数(i=0,1,…,n)
( x x0 )(x x2 ) ( x x0 )(x x1 ) ( x x1 )(x x2 ) P( x) y0 y1 y2 ( x0 x1 )(x0 x2 ) ( x1 x0 )(x1 x2 ) ( x2 x0 )(x2 x1 )
容易看出,P(x)满足条件
( x 0 , y0 ), ( x1 , y1 ), ( x 2 , y2 ) 的抛物线 y P( x) 近似代替曲线
y f ( x) ,如下图所示。因此也称之为抛物插值。
P(x)的参数 a0 , a1 , a 2
直接由插值条件决定， 即
y
a0 , a1 , a2满足下面
O
y=L2(x) y0 x0 y1 x1 y1 x2 y=f(x) x
( x x0 )(x x1 ) l 2 ( x) ( x2 x0 )(x2 x1 )
这样构造出来的 l0 ( x),l1 ( x),l2 ( x) 称为抛物插值的基函数 取已知数据 y0 , y1 , y 2 作为线性组合系数,将基函数
l0 ( x),l1 ( x),l2 ( x) 线性组合可得
a n x0 n a n 1 x0 n 1 a1 x0 a 0 f ( x0 ) n n 1 a n x1 a n 1 x1 a1 x1 a 0 f ( x1 ) a x n a x n 1 a x a f ( x ) n 1 n 1 n 0 n n n
数值分析第二章 插值法

数值分析第二章 插值法


(j,k=0,1,…,n)
( x x0 )( x xk 1 )( x xk 1 )( x xn ) lk ( x ) ( xk x0 )( xk xk 1 )( xk xk 1 )( xk xn )
n1 ( x ) ( x xk ) n1 ' ( xk )
n
• 均差的计算
三、均差与牛顿插值
1.均差与性质
• 均差定义
• 性质 （2）k阶均差可重新写为：
f [ x1 , x2 ,, xk ] f [ x0 , x1 , xk 1 ] f [ x0 , x1 , xk ] xk x0
• 均差的计算
三、均差与牛顿插值
1.均差与性质
• 均差定义
类似地称 2 f k f k 1 f k 为 xk 处的二阶差分. 一般地称 n f k n1 f k 1 n1 f k 为 xk 处的n阶差分.
• 均差与差分关系
• 牛顿前插公式
n f k (1) f nk j , j 0 j
求5、6月份的日照时间的变化规律。 • 多项式插值的存在唯一性
一、引言
2.多项式插值
• 一个例子 日照时间的变化设为 y(x)=a0+ a1x + a2x2, 根据三组数据: (1, 13.53), (31, 14.21),(61, 14.40)， 导出关于a0，a1，a2的线性方程组
a0 a1 a2 13.53 2 a0 31a1 (31) a2 14.21 2 a0 61a1 (61) a2 14.40
三、均差与牛顿插值
3.差分形式的牛顿插值公式
若x0,x1,…,xn 为等距节点，即xk=x0+kh (k=0,1,...,n) 时，可将牛顿插值公式简化
数值分析_第二章_插值法

数值分析_第二章_插值法


１ x０
x２ ０
ቤተ መጻሕፍቲ ባይዱ
…
xn－ １ ０
…… ………
V n－ １ （ x０ ，x１ ，… ，xn－ １ ） ＝
１
xn－ ２
x２ n－ ２
…
xn－ １ n－ ２
１
xn－ １
x２ n－ １
…
xn－ １ n－ １
∏ ＝
（ xi － xj ） ．
０ ≤ j ＜ i ≤ n－ １
故 知 V n （ x） ＝ V n－ １ （ x０ ，x１ ，… ，xn－ １ ）（ x － x０ ）（ x － x１ ） … （ x －
＝ R截 ＋ R舍
＝
f″２（！ξ）（ x －
xi ）（ x －
xi＋ １ ） ＋
×
（－
０
．６９３１４７）
＋
（０ ．５４ （０ ．６
－ －
０ ０
．４）（０ ．４）（０
．５４ － ０ ．５） ．６ － ０ ．５）
× （ － ０ ．５１０８２６） ≈ － ０ ．６１５３２０ ．
４畅 解
由题设知 ０° ≤
x≤
９０° ，h ＝
xi＋ １
－
xi
＝
（
１ ６０
）°
．记
xi
处的准确值为 f i ，带有误差的值为 f i ，则
７ ，
x
∈
［１ ，２］ ，
－
１９ ２
x３
＋ ６７ x２
－
２９３ ２
x
＋
１０５ ，
x
∈
（２ ，３］ ．
四 、习题
１畅 根据范德蒙行列式的定义 ，令
V n （ x） ＝ V n （ x０ ，x１ ，… ，xn－ １ ，x）
数值分析作业答案

数值分析作业答案

第2章 插值法1、当x=1，-1，2时，f(x)=0，-3，4，求f(x)的二次插值多项式。

（1）用单项式基底。

（2）用Lagrange 插值基底。

（3）用Newton 基底。

证明三种方法得到的多项式是相同的。

解：（1）用单项式基底设多项式为:2210)(x a x a a x P ++=，所以：6421111111111222211200-=-==x x x x x x A 37614421111111424113110111)()()(222211200222221112000-=-=---==x x x x x x x x x f x x x f x x x f a 2369421111111441131101111)(1)(1)(12222112002222112001=--=--==x x x x x x x x f x x f x x f a 6565421111111421311011111)(1)(1)(12222112002211002=--=---==x x x x x x x f x x f x x f x a 所以f(x)的二次插值多项式为：2652337)(x x x P ++-= （2）用Lagrange 插值基底)21)(11()2)(1())(())(()(2010210-+-+=----=x x x x x x x x x x x l)21)(11()2)(1())(())(()(2101201------=----=x x x x x x x x x x x l)12)(12()1)(1())(())(()(1202102+-+-=----=x x x x x x x x x x x lLagrange 插值多项式为：372365)1)(1(314)2)(1(61)3(0)()()()()()()(22211002-+=+-⨯+--⨯-+=++=x x x x x x x l x f x l x f x l x f x L所以f(x)的二次插值多项式为：22652337)(x x x L ++-= (3) 用Newton 基底: 均差表如下：Newton 372365)1)(1(65)1(230))(](,,[)](,[)()(21021001002-+=+-+-+=--+-+=x x x x x x x x x x x x f x x x x f x f x N所以f(x)的二次插值多项式为：22652337)(x x x N ++-= 由以上计算可知，三种方法得到的多项式是相同的。

Ch2插值法

Ch2插值法

Ch2. 插值法§1. 插值问题引例 矿井中某处的瓦斯浓度y 与该处距地面的距离x 有关，现用仪器测得从地面到井下500米每隔50米的瓦斯浓度数据(,)(0,1,2,,10)= i i x y i ，根据这些数据完成下列工作：(1)寻找一个函数，要求从此函数中可近似求得从地面到井下500米之间任意一点处的瓦斯浓度；(2)估计井下600米处的瓦斯浓度。

第一个问题可归结为“已知函数在n x x x ,,,10⋅⋅⋅处的值，求函数在区间[]n x x ,0内其它点处的值”，这种问题适宜用插值方法解决。

但对第二个问题不宜用插值方法，因为600米已超出所给数据范围，用插值函数外推插值区间外的数据会产生较大的误差。

解决第二个问题的常用方法是，根据地面到井下500处的数据求出瓦斯浓度与地面到井下距离之间的函数关系)(x f ，由)(x f 求井下600米处的瓦斯浓度。

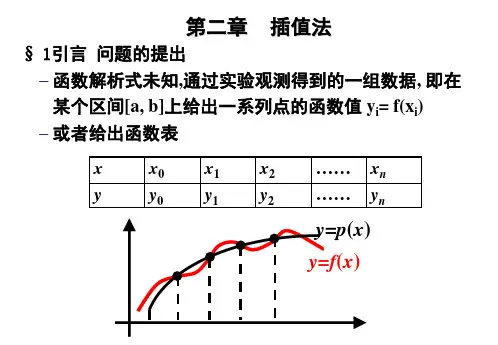
定义 设)(x f y =在[]b a ,中1+n 个点n x x x <⋅⋅⋅<<10处的值)(i i x f y =为已知，现根据上述数据构造一个简单函数)(x p ，使i i y x p =)(，这种问题称为插值问题。

i x x p x f ),(),(,i i y x p =)(分别称为被插值函数、插值函数、插值节点和插值条件。

若)(x p 为多项式，则此问题称为多项式插值或代数插值。

定理1 在插值节点n x x x ,,,10⋅⋅⋅处，取给定值n y y y ,,,10⋅⋅⋅，且次数不高于n 的插值多项式是存在且唯一的。

证 令n n x a x a a x p +⋅⋅⋅++=10)(，则根据插值条件i i y x p =)(有下列等式：⎪⎪⎩⎪⎪⎨⎧=+⋅⋅⋅++=⋅⋅⋅⋅⋅⋅=+⋅⋅⋅++==+⋅⋅⋅++=n n n n n n nn nn yx a x a a x p y x a x a a x p y x a x a a x p 10111101000100)()()( （关于i a 的1+n 阶线性方程组）， 其系数行列式是范德蒙（V andermonde ）行列式()011111100≠-=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=∏≥>≥j i n j innnnn x xx x x x x x D 。

《数值分析》第二讲插值法PPT课件

《数值分析》第二讲插值法PPT课件


1 xn xn2 xnn Vandermonde行列式
即方程组（2）有唯一解 (a0, a1, , an)
所以插值多项式
P (x ) a 0 a 1 x a 2 x 2 a n x n
存在且唯一
第二章：插值
§2.2 Lagrange插值
y
数值分析
1、线性插值
P 即(x)ykx yk k 1 1 x yk k(xxk)
l k ( x k 1 ) 0 ,l k ( x k ) 1 ,l k ( x k 1 ) 0 l k 1 ( x k 1 ) 0 ,l k 1 ( x k ) 0 ,l k 1 ( x k 1 ) 1
lk1(x)(x(k x 1 x xk k))x x ((k 1x k x 1k )1) lk(x)((xx k x xk k 1 1))((x xkxx k k1)1)
第二章：插值
数值分析
3、Lagrange插值多项式
令 L n ( x ) y 0 l 0 ( x ) y 1 l 1 ( x ) y n l n ( x )
其中，基函数
lk (x ) (x ( k x x x 0 ) 0 ) (( x x k x x k k 1 1 ) )x x k ( ( x x k k 1 ) 1 ) (( x x k x n x )n )
因此 P (x ) lk (x )y k lk 1 (x )y k 1
且
P (x k ) y k P (x k 1 ) y k 1
lk(x), lk1(x) 称为一次插值基函数
数值分析
第二章：插值
2、抛物线插值 令
y (xk , yk )
f (x)
lk1(x)(x(k x 1 x xk k))x x ((k 1x k x 1k )1) p( x) (xk1,yk1)
数值分析(第5版)第2章-插值法 ppt课件

数值分析(第5版)第2章-插值法 ppt课件



x4 94

1(x 5
4)
插值多项式为
1
1
L1( x)
y0l0 ( x) y1l1( x) 2
5
( x 9) 3 ( x 4) 5
2 ( x 9) 3 ( x 4) 1 ( x 6)
5
5
5
所以
7

L1 (7)

13 5

2.6
ppt课件
项式(2-2) 存在且唯一。证毕。
ppt课件
5
第二节 拉格朗日插值
一、基函数
考虑下面最简单`最基本的插值问题。求n 次多项 式 l i(x) (i=0,1, …, n)，使其满足条件
0 , j i li ( xj ) 1, j i ( j 0,1, , n)
故可设
li ( x) A( x x0 )( x xi1 )( x xi1 )( x xn )
15
例2 求过点(1,2), (1,0), (3,6), (4,3)的三次插值多项式。
解 以 x0 1, x1 1, x2 3, x3 4 为节点的基函数
分别为:
l0
(
x)

( x 1)( x 3)( x 4) (1 1)(1 3)(1 4)

Pn(x)=a0+a1x+a2x2+...+anxn (2-2)
则由插值条件式Pn(xi)=yi (i=0,1, ..., n) 可得关于系数 a0 ,a1 , …,an的线性代数方程组
ppt课件
3

a0 a0

a1 x0 a1 x1
数值分析 第2章 插值法

数值分析 第2章 插值法

代入抛物插值公式得：
115 (115 121)(115 144) 10 (100 121)(100 144)
(115 100)(115 144) 11 (121 100)(121 144) (115 100)(115 121) 12 10.7228 (144 100)(144 121)
几何意义：y=p1(x)表示通过三点（x0,y0), (x1,y1) , (x2,y2)的抛物线，因此，二次插值 又称抛物插值。
p2(x)的解？
先解决一个特殊的二次插值问题
特殊的二次插值问题
求作二次式l0(x),使满足条件 l0(x0)=1 ， l0(x1)= l0(x2)=0
由l0(x1)= l0(x2)=0 可知：x1,x2是l0(x)的两个零点，因而有：
4x x
带入x0=100, 得
f
(x 0)
10,f
(x 0 )

1 ,f
20
(x 0 )


1 4000
p1(x ) f (x 0 ) f (x 0 )(x x 0 ) 5 0.05x
p2(x )

p1(x )
f
(x 0 ) (x
2!
x 0)2
计算 115的近似值 （精确值10.723805…）
2!

x0)
10.75 0.028125 10.721875
练习：求作f(x)=sin x在节点x0=0的5次泰勒多项式，并估计插 值误差。
解：f (x ) cos x ,f (x ) sin x ,f (3)(x ) cos x , f (4)(x ) sin x ,f (5)(x ) cos x
数值分析 插值法

数值分析 插值法

第二章 插值法在科学研究与工程技术中，常常遇到这样的问题：由实验或测量得到一批离散样点，要求作出一条通过这些点的光滑曲线，以便满足设计要求或进行加工。

反映在数学上，即已知函数在一些点上的值，寻求它的分析表达式。

此外，一些函数虽有表达式，但因式子复杂，不易计算其值和进行理论分析，也需要构造一个简单函数来近似它。

解决这种问题的方法有两类：一类是给出函数()f x 的一些样点，选定一个便于计算的函数()x ϕ形式，如多项式、分式线性函数及三角多项式等，要求它通过已知样点，由此确定函数()x ϕ作为()f x 的近似，这就是插值法；另一类方法在选定近似函数的形式后，不要求近似函数过已知样点，只要求在某种意义下在这些样点上的总偏差最小。

这类方法称为曲线（数据）拟合法。

设已知区间[,]a b 上的实值函数f 在1n +个相异点[,]i x a b ∈处的函数值(),0,1,,i if f x i n ==，要求构造一个简单函数()x ϕ作为函数()f x 的近似表达式()()f x x ϕ≈使得()(),0,1,,i i i x f x f i n ϕ=== (2-1)这类问题称为插值问题。

称f 为被插值函数；()x ϕ为插值函数；0,,n x x 为插值节点；(2-1)为插值条件。

若插值函数类{()}x ϕ是代数多项式，则相应的插值问题为代数插值。

若{()}x ϕ是三角多项式，则相应的插值问题称为三角插值。

若{()}x ϕ是有理分式，则相应的插值问题称为有理插值。

§1 Lagrange 插值1.1 Lagrange 插值多项式设函数f 在1n +个相异点01,,,n x x x 上的值(),0,1,,i i f f x i n ==是已知的，在次数不超过n 的多项式集合n P 中，求()n L x 使得(),0,1,,n i i L x f n n == (2-2)定理1 存在惟一的多项式n nL P ∈满足插值条件(2-2)。

数值分析--第2章 插值法

数值分析--第2章 插值法

数值分析--第2章插值法第2章 插值法在科学研究与工程技术中，常常遇到这样的问题：由实验或测量得到一批离散样点，要求作出一条通过这些点的光滑曲线，以便满足设计要求或进行加工。

反映在数学上，即已知函数在一些点上的值，寻求它的分析表达式。

此外，一些函数虽有表达式，但因式子复杂，不易计算其值和进行理论分析，也需要构造一个简单函数来近似它。

解决这种问题的方法有两类：一类是给出函数)(x f 的一些样点，选定一个便于计算的函数)(x ϕ形式，如多项式、分式线性函数及三角多项式等，要求它通过已知样点，由此确定函数)(x ϕ作为)(x f 的近似，这就是插值法；另一类方法在选定近似函数的形式后，不要求近似函数过已知样点，只要求在某种意义下在这些样点上的总偏差最小。

这类方法称为曲线（数据）拟合法。

设已知函数f 在区间],[b a 上的1+n 个相异点ix 处的函数值(),0,,iif f x i n ==，要求构造一个简单函数()x ϕ作为函数()f x 的近似表达式()()f x x ϕ≈，使得()(),0,1,,iiix f x f i n ϕ=== (2-1) 这类问题称为插值问题。

称f 为被插值函数；()x ϕ为插值函数；nx x ,,0 为插值节点；(2-1)为插值条件。

若插值函数类{()}x ϕ是代数多项式，则相应的插值问题为代数插值。

若{()}x ϕ是三角多项式，则相应的插值问题称为三角插值。

若{()}x ϕ是有理分式，则相应的插值问题称为有理插值。

§1 Lagrange 插值1.1 Lagrange 插值多项式设函数f 在1+n 个相异点01,,,nx x x 上的值n i x f f ii ,,1,0),( ==是已知的，在次数不超过n 的多项式集合n P 中，求()nL x 使得(),0,1,,n i iL x f n n == (2-2) 定理2.1 存在惟一的多项式nn P L ∈满足插值条件(2-2)。

第二章 插值法-数值分析


1 1
x0 x1
2 n x0 x0 2 n x1 x1
2 n 1 xn xn xn Nhomakorabea
0 i j n

( x j - xi ) 0
由克莱默法则知，方程组有唯一解 a0 , a1 , , an .
§2 Lagrange Polynomial
唯一性的另一证明 满足 P( xi ) yi , i 0, ... , n 的 n 阶插 值多项式是唯一存在的。
分别利用x0, x1 以及 x1, x2 计算
x0

利用 x1 , x2
4
3
~ 5 0 . 00538 R 0.00660 sin 50 0.76008, 1 18
内插 /* interpolation */ 的实际误差 0.00596
§1 Lagrange Polynomial
i 0 n
多项式，其中 p( x )可以是任意多项式。
Interpolation polynomial

2-2 线性插值与抛物插值 1. 线性插值
f (x)
(x0 ,y0) (x1 ,y1)
P1(x)
x0
x1
y1 - y 0 ( x - x0 ) 直线方程为: y - y 0 x1 - x0 x - x0 x - x1 等价变形为: y x - x y 0 x - x y1 0 1 1 0
可见 P1(x) 是过 ( x0 , y0 ) 和 ( x1, y1 ) 两点的直线。
记为: L1 ( x)
引入记号:
x - x1 l 0 ( x) , l1 ( x) x - x0 x0 - x1 x1 - x0

第2讲：插值法

i 0
n
为满足条件 Ln ( xk ) yk , (k 0, 1, , n) 的 n 次Lagrange插值多项式，则对任意 x [a , b]
第二章：插值
数值分析
有
f ( n1) ( ) Rn ( x ) f ( x ) Ln ( x ) n1 ( x ) (n 1)!
p( x )
sin x
3 2
y
x
2
o

2

第二章：插值
数值分析
1、插值的基本概念
设函数 y f ( x) 在区间 a, b 有定义，且在已知点：
y0 , y1 , , yn a x0 x1 xn b 上的函数值为：
如果存在一个简单函数 y p( x) 使 yi p( xi )
0.330365
解：
第二章：插值
数值分析
f ( n1) ( ) 由 Rn ( x ) f ( x ) Ln ( x ) n1 ( x ) (n 1)! sin 得 R1 ( x ) ( x 0.32)( x 0.34) 2
| sin | | 0.3367 0.32 || 0.3367 0.34 | 于是 | R1 (0.3367) | 2 sin0.34 0.0167 0.0033 0.0000091892 34 2
0.330387
f ( n1) ( ) 由 Rn ( x ) f ( x ) Ln ( x ) n1 ( x ) (n 1)! sin ~ 得 R1 ( x ) ( x 0.34)( x 0.36) 2
第二章：插值
数值分析
于是
| sin | ~ | R1 (0.3367) | | 0.3367 0.34 || 0.3367 0.36 | 2 sin0.36 0.0033 0.0233 0.0000135431 7 2

数值分析第二章 插值法

i =0 n
多项式，其中 p( x )可以是任意多项式。
推论
§1 Lagrange Polynomial
插值余项 /* Remainder */
设节点 a x0 x1 xn b f ( n) ( x)在[a, b]上连续 f ( n1)在[a , b]内存在, 考察截断误差 R ( x) = f ( x) - L ( x) n n
li ( xi ) = 1
Ci =
1 j i ( xi - x j )
与 节点 有关，而与 f 无关
ቤተ መጻሕፍቲ ባይዱ
Lagrange Polynomial
(x - xj ) li ( x ) = ( xi - x j ) ji
n j =0
Ln ( x ) = l i ( x ) yi
i =0
n
§1 Lagrange Polynomial

sin 50 = 0.7660444…
2次插值的实际误差 0.00061 高次插值通常优于 低次插值 但绝对不是次数越 高就越好，嘿 嘿……
课堂作业
1. 当x = 1,-1,2时, f ( x) = 0,-3,4, 求f ( x)的二次插值多项式 2.
已知由数据 (0,0), (0.5, y), (1,3)和(2,2)构造出的 3 三次插值多项式 P ( x ) 的 x 的系数是 6,试确定数据 y 3
=
x - x1 y + x 0 - x1 0
x - x0 y = x1 - x 0 1
l ( x) y
i =0 i
1
i
l0(x)
l1(x)
§1 拉格朗日多项式
例1
/* Lagrange Polynomial */

《数值分析》课件-第2章


（1）
则称ϕ (x)
为
f
(x)
在
Φ
中关于节点
{xi
}n i=0
的一个插值函数。
f (x) ——被插值函数； [a, b] ——插值区间；
{xi
}n i=0
——插值节点；
式（1）——插值条件.
2004-9-9
3
2 . 几何意义、内插法、外插法
M~
=
max{x
i
}n i =0
m~
=
min{x
i
}n i =0
2004-9-9
内插
x ∈[m~, M~ ]
外插 x ∈[a, b] but x ∉[m~, M~ ]
4
3. 多项式插值问题
对于不同的函数族Φ的选择，得到不同的插值 问题
当Φ为一些三角函数的多项式集合时:三角插值; 当Φ为一些有理分式集合时：有理插值； 当Φ为一些多项式集合时：多项式插值
{ } 特别的取 Φ = Pn =∆ span 1, x, x2 ,L, xn , 即
g
(t )
在区间
[a,
b]
上的
n
+
2
个互异零点：
x
、
{xi
}n i=0
当 g(t) 充分光滑时， g (n+1) (t) 在开区间 (a, b) 内至少存在一个零点ξ
g g
(n (n
+1) +1)
(t) =
(ξ ) =
f( 0
n+1)
(t
)
−
(n
+
1)!k
(
x)
⇒
k
(

数值分析第二章 插值总结


j=0
n
Ln ( x) = li ( x) yi i=0
与节点有关，而与 f无关
Lagrange Polynomial
§2 Lagrange Polynomial
定理 (唯一性) 满足 P( xi ) = yi , i = 0, ... , n 的 n 阶插值多
项式是唯一存在的。
证明： ( 前面已利用Vandermonde 行列式论证) 反证：若不唯一，则除了Ln(x) 外还有另一 n 阶多项 式 Pn(x) 满足 Pn(xi) = yi 。 考察 Qn( x) = Pn( x) - Ln( x) , 则 Qn 的阶数 n 而 Qn 有 n + 1个不同的根 x0 … xn
插值
Interpolation_introduction
插值节点 插值条件
---插值问题
多项式插值是数值分析的基本工具，常用来计算被插函数 的近似函数值，零、极点，导数、积分（第四章 数值积分 和数值微分），解微分方程（第五章）、积分方程
Interpolation polynomial
多项式插值----polynomial interpolation
高就越好，嘿 嘿……
Oh yWReahigheh?nt.yWoTuhaestntiafarIltlfwinrditing the program,
wyottihhlunleeWomhwcLtaeoiuvaaltrwlehcrgefricerietlniaTluonnLdnchrttabageoehigetremneoprtrabweyoeeenaorln-Etaepgcsouotxaaoieiusdcmnsllc,pgaeiygsiultohlgiilci(plole?thaxyuonnittn)sseit,wnosdtptmoa.stohniciiaintnasltt.tloocp! urtaoalcabkcteleeomunt.

数值分析课件-第02章插值法

数值分析课件-第02章插值法
目录
• 插值法基本概念与原理 • 拉格朗日插值法 • 牛顿插值法 • 分段插值法 • 样条插值法 • 多元函数插值法简介
01 插值法基本概念与原理
插值法定义及作用
插值法定义
插值法是一种数学方法，用于通过已知的一系列数据点，构造一个新的函数， 使得该函数在已知点上取值与给定数据点相符，并可以用来估计未知点的函数 值。
06 多元函数插值法简介
二元函数插值基本概念和方法
插值定义
通过已知离散数据点构造一个连 续函数，使得该函数在已知点处
取值与给定数据相符。
插值方法分类
根据构造插值函数的方式不同， 可分为多项式插值、分段插值、
样条插值等。
二元函数插值
针对二元函数，在平面上给定一 组离散点，构造一个二元函数通 过这些点，并满足一定的光滑性
差商性质分析
分析差商的性质，如差商 的对称性、差商的差分表 示等，以便更好地理解和 应用差商。
差商与导数关系
探讨差商与原函数导数之 间的关系，以及如何利用 差商近似计算导数。
牛顿插值法优缺点比较
构造简单
牛顿插值多项式构造过程相对简 单，易于理解和实现。
差商可重用
对于新增的插值节点，只需计算 新增节点处的差商，原有差商可 重用，节省了计算量。
要求。
多元函数插值方法举例
多项式插值
分段插值
样条插值
利用多项式作为插值函数，通 过已知点构造多项式，使得多 项式在已知点处取值与给定数 据相符。该方法简单直观，但 高阶多项式可能导致Runge现 象。
将整个定义域划分为若干个子 区间，在每个子区间上分别构 造插值函数。该方法可以避免 高阶多项式插值的Runge现象 ，但可能导致分段点处的不连 续性。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

在有些情况下，虽然可以写出函数 f ( x ) 的解析表达式， 但由于结构相当复杂，使用起来很不方便。面对这些情况， 总希望根据所得函数表（或结构复杂的解析表达式），构造 某个简单函数 P( x ) 作为 f ( x ) 的近似。
插值法是解决这类问题的一种比较古老，然而却是目前 常用的方法，它不仅直接广泛应用于生产实际和科学研究 中，而且也是进一步学习数值分析计算方法的基础。
y L1(x)的几何意义就是通过两点（xk , yk )与（xk1, yk1)的直线，
如上图所示，L（1 x）的表达式可由几何意义直接给出：
y
y L1(x)
Байду номын сангаас
y f (x)
yk
y k 1
0
xk
x xk 1
L1 (x)
yk
yk 1 xk 1
yk xk
(x
xk )
L1 (x)
xk1 x xk1 xk
lk1 (x)是二次函数，且在节点上满足： lk1 (xk1 ) 1.lk1 (x j ) 0. （j=k-1,k)
lk (xk ) 1.lk (x j ) 0
(j=k-1,k+1)
lk1 (xk1 ) 1.lk1 (x j ) 0 (j=k,k+1)
满足条件（8）的插值基函数是容易求出的。例如lk1 (x).有两个零点xk1 xk .故可表示为：lk1 (x) A(x xk1 )(x xk )其中A为待定系数，由条件 lk1 (xk1 ) 1可得：
pn (x) a0 a1x a2 x2 an xn
（2）
使 pn (xi ) yi
其中 a0a1 an 为变数
xi , yi意义同前
（3）
满足插值条件（3）的多项式（2）称为函数 f(x)在节点 xi（i=0，1
…n ）处的n次插值多项式。 求函数 f(x) 的n次插值多项式的几何意义是：
a0a1 an 得到。但这样做不但计算复杂，而且难于得到
P(x)的简单表达式。为求得便于使用的简单插值多项式 p(x)，我们
先讨论n=1的情形。
假定已知区间 xk , xk1 的端点处的函数值 yk f (xk ), yk1 f (xk1)
要求线性插值多项式 L1 (x)。满足： L1 (xk ) yk , L1 (xk1 ) yk1
yk
x xk xk1 xk
yk 1
（点斜式） （两点式）
由两点式可看出， L1 (x)是由两个线性函数
lk (x)
x xk1 xk xk 1
lk1 (x)
x xk xk 1 xk
（6）
的线性组合得到的。其系数分别为 yk 及yk1,即：
L1 (x) yk lk (x) yk1lk1 (x)
1 x0 x02 x0n
1 vn (x0 , x1,xn )
x1
x12
x1n
1 xn xn2 xnn
（5）
不为零，式中 vn (x0 , x1 xn )称为范德蒙（Vandermonde)行列式。
利用行列式性质可得：
n i1
vn (x0, x1xn )
(xi x j )
i1 j0
通过曲线y=f(x)上的n+1个点（ xi , yi ）（i=0,1…n）作一条n次代数
曲线y= pn(x)作为曲线 y= f(x)的近似。如下图。
y
y0 y1
0 a x0 x1
yn
xn b x
设p(x)是形如（2）的插值多项式，用 Hn 代表所有次数不超过n的
多项式集合，于是p(x) Hn ，所谓插值多项式p(x)存在唯一，就是
（7）
lk
(
x),l
k
1
(
x)也是线性插值多项式，在节点xk
及xk
上满足条件：
1
lk (x) 1.lk (xk1 ) 0, lk1 (xk ) 0, lk1 (xk1 ) 1.
我们称函数lk (x)及lk1 (x)为线性插值基函数。见下图：
y 1
lk (x)
0
xk
xk 1 x
y 1
lk1 (x) 0 xk
xk 1
x
下面讨论n 2的情形。
假定插值节点为xk1, xk , xk1,要求二次插值多项式L（2 xi ) yi (i k 1, k,
k 1)
几何上y L2 (x)就是通过三点（xk1, yk1 ).(xk , yk ),(xk1, yx1 )的抛物线。
为了求出L2的表达式，可采用基函数方法，此时基函数lk1 (x),lk (x)及
插值函数类Φ的取法不同，所求得的插值函数 p(x)逼近f(x)的效果就不同。而它的选择主要取决 于使用需要。常用的代数多项式、三角多项式和有 理函数等。
当选用代数多项式作为插值函数时，相应的插值问题就称为多项式 插值。本章讨论的即为此类问题。
在多项式插值中，最常见、最基本的问题是：
求一个次数不超过n的代数多项式：
指在集合H n中有且只有一个p(x)满足（3）。由（3）得：
a0 a0
a1 x0 a1 x1
a2 x02 a2 x12
an x0n an x1n
y0 y1
(4)
a0
a1xn
a2
x
2 n
an xnn
yn
这是一个关于a0a1 an的n+1元线性方程组。
要证明插值多项式存在且唯一，只要证明方程组（4）存在唯一的解， 也就是证明方程组（4）的系数行列式
设 y f (x)在区间 [a,b] 上连续，且在 n 1个不同的点
a x0 x1 xn b
上的值分别为 y0 , y1, , yn .
插值的目的就是要在一个性质优良、便于计算的 函数类 中，求一简单函数 P(x),使 P(xi ) yi (i 0,1,L , n) (I ) 而在其它点 x xi 上，P(x)作为 f (x) 的近似。
由于 i j 时 xi x j，故所有因子 xi x j 0 ，于是 vn (x0 , x1,xn ) 0
故方程组（4）存在唯一的一组解 a0 , a1 an. 由此有结论： 定理1： 若节点 x0、x1xn 互不相同，则满足插值条件（3）的n
次插值多项式（2）存在且唯一。
由定理1的证明可见，要求插值多项式 p(x)，可以通过求方程 组（4）的解:
在生产和科研中出现的函数是多种多样的，常遇到这样的
情况：在某个实际问题中，虽可断定所考虑的函数 f (x) 在区间 [a , b ]上存在且连续，但却难以找到它们的解析表达式，只能通 过实验和观测得到在这有限个点上的函数值（即一张函数表)来 分析函数 f (x ) 的性态，甚至直接求出其它一些点上的函数值可 能是十分困难的。