小学五年级数学竞赛奥数讲义-例题word百度文库

第 21 讲假设法解题基础卷1．小明有 2 元和 5 元的邮票共 100 枚，总价钱为 320 元，这两种邮票各有多少枚？5×100＝500元，500－320＝180元2元：180÷﹙5－2﹚＝60枚5元：100－60＝40枚2．松鼠妈妈采松子，晴天每天可以采 20 个，雨天每天只能采 12 个。

它一连几天采了 112 个松子，平均每天采 14 个。

问：这几天当中有几天有雨？采了：112÷14=8天假设全是晴天应该采 20×8=160个比实际少了 160-112=48个是由于把雨天也看成了晴天每天相差 20-12=8个雨天：48÷8=6天3．徒工小王雕刻红木玩具，平均每天雕刻玩具 48 件。

每雕刻出一件正品，可创造财富 12 元：但如果雕刻坏了一件就要损失 98 元。

他平均每天创造财富 466 元。

小王平均每天雕刻出的正品是多少件？可以这么列：（48×12－466）÷（12＋98）＝1（件）48－1＝47（件）4．数学竞赛中抢答题共 10 道题，规定答对一题得 15 分，答错一题倒扣 10 分（不答按答错计算）。

晓敏回答了所有的问题，结果共得 100 分，问：答对和答错各几题？设答对x题,答错（10-x）题.15x-10（10-x）=10015x+10x-100=10025x=200x=8∴答错10-8=2题答：答对8题,答错2题.5．学校组织春游，一共用了 10 辆客车，已知大客车每辆坐 100 人，小客车每辆坐 60 人，大客车比小客车一共多载 520 人，问：大、小客车各几辆？假设大客车为x辆,小客车则为10-x ,又大客车多坐520人那么100*x-520= 60*（10-x）求得x=7所以7辆大客车,3辆小客车6．人民电影院有座位 1200 个，前排票每张 1.5 元，后排票每张 2.5 元。

已知后排票比前排票的总价多1080 元，该电影院有前排座位和后排座位各多少个？假设前排和后排的座位是相同的,那么后排票会比前排票总价多600元（1200除以2等于600, ,2.5减1.5等于1,1X600=600）而现在实际多了1080元,1080—600=480元因此相当于少算了480除以4等于120个后排的座位.（本来是后排就是2.5却被算成前排,对于后排来说就相差2.5加1.5等于4元）所以前排有600-120=480个座位,后排有600+120=720个座位.1200÷2=600（元） 1080—600=480（元）后排：480÷（2.5+1.5）+600=720（个）前排：1200-720=480（个）提高卷1．有 1 元硬币和 5 角硬币若干枚，共值 675 角。

第1讲平均数(一)一、知识要点把几个不相等的数，在总数不变的条件下，通过移多补少，使它们完全相等，求得的相等的数就是平均数。

如何灵活运用平均数的数量关系解答一些稍复杂的问题呢？下面的数量关系必须牢记：平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量×平均数二、精讲精练【例题1】有4箱水果，已知苹果、梨、橘子平均每箱42个，梨、橘子、桃平均每箱36个，苹果和桃平均每箱37个。

一箱苹果多少个？【思路导航】（1）1箱苹果＋1箱梨＋1箱橘子=42×3=136（个）；（2）1箱桃＋1箱梨＋1箱橘子=36×3=108（个）（3）1箱苹果＋1箱桃=37×2=72（个）由（1）（2）两个等式可知：1箱苹果比1箱桃多126－108=18（个），再根据等式（3）就可以算出：1箱桃有（74－18）÷2=28（个），1箱苹果有28＋18=46（个）。

1箱苹果和1箱桃共有多少个：37×2=74（个）1箱苹果比1箱桃多多少个：42×3－36=18（个）1箱苹果有多少个：28＋18=46（个）练习1：1.一次考试，甲、乙、丙三人平均分91分，乙、丙、丁三人平均分89分，甲、丁二人平均分95分。

问：甲、丁各得多少分？2.甲、乙、丙、丁四人称体重，乙、丙、丁三人共重120千克，甲、丙、丁三人共重126千克，丙、丁二人的平均体重是40千克。

求四人的平均体重是多少千克？3.甲、乙、丙三个小组的同学去植树，甲、乙两组平均每组植树18棵，甲、丙两组平均每组植树17棵，乙、丙两组平均每组植树19棵。

三个小组各植树多少棵？【例题2】一次数学测验，全班平均分是91.2分，已知女生有21人，平均每人92分；男生平均每人90.5分。

求这个班男生有多少人？【思路导航】女生每人比全班平均分高92－91.2=0.8（分），而男生每人比全班平均分低91.2－90.5=0.7（分）。

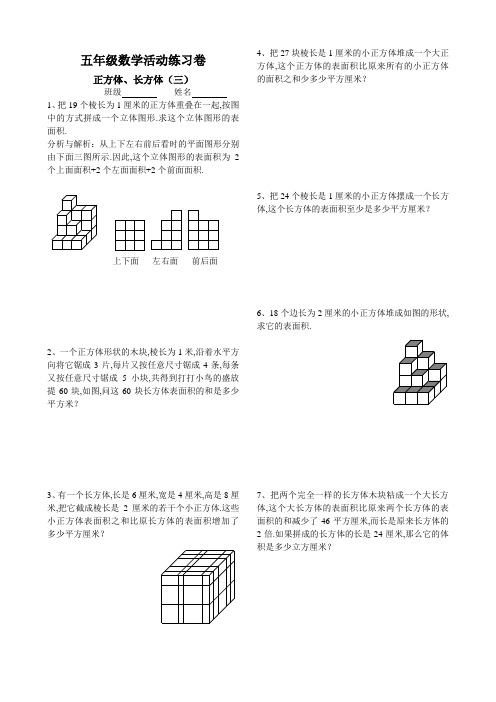
五年级数学活动练习卷正方体、长方体（三）班级姓名1、把19个棱长为1厘米的正方体重叠在一起,按图中的方式拼成一个立体图形.求这个立体图形的表面积.分析与解析：从上下左右前后看时的平面图形分别由下面三图所示.因此,这个立体图形的表面积为2个上面面积+2个左面面积+2个前面面积.上下面左右面前后面2、一个正方体形状的木块,棱长为1米,沿着水平方向将它锯成3片,每片又按任意尺寸锯成4条,每条又按任意尺寸锯成5小块,共得到打打小鸟的盛放提60块,如图,问这60块长方体表面积的和是多少平方米？3、有一个长方体,长是6厘米,宽是4厘米,高是8厘米,把它截成棱长是2厘米的若干个小正方体.这些小正方体表面积之和比原长方体的表面积增加了多少平方厘米？4、把27块棱长是1厘米的小正方体堆成一个大正方体,这个正方体的表面积比原来所有的小正方体的面积之和少多少平方厘米？5、把24个棱长是1厘米的小正方体摆成一个长方体,这个长方体的表面积至少是多少平方厘米？6、18个边长为2厘米的小正方体堆成如图的形状,求它的表面积.7、把两个完全一样的长方体木块粘成一个大长方体,这个大长方体的表面积比原来两个长方体的表面积的和减少了46平方厘米,而长是原来长方体的2倍.如果拼成的长方体的长是24厘米,那么它的体积是多少立方厘米？8、有一个长方体,长10厘米,宽6厘米,高4厘米,如果把它锯成棱长是1厘米的小正方体,一共能锯成多少个？这些小正方体的表面积和是多少？9、有一个正方体,棱长是3分米.如果按下图把它切成棱长是1分米的小正方体,这些小正方体的表面积的和是多少？10、用棱长是1厘米的小正方体摆成一个稍大一些的正方体,至少需要多少个小正方体？如果摆成一个棱长是6厘米的正方体,需要多少个小正方体？11、下图是一个棱长为3厘米的正方体,一只蚂蚁从A点沿表面爬向B点.请画出蚂蚁爬行的最短路线.这样的路线共有几条？BA12、右图是由16个棱长2厘米的小正方体重叠而成的,求这个立体图形的表面积.13、如图,由22个棱长1厘米的正方体组成,求表面积为多少？图中有多少个由两个正方体组成的长方体？14、一长方体,如图,从这个长方体上切下一个长宽高为连续自然数的最大长方体,连续切三次后,最后得到长方体的体积是多少？1065。

五年级奥数讲义：棋盘中的数学（含答案）1．棋盘中的图形与面积；2．棋盘中的覆盖问题：（1）概念：用某种形状的卡片，按一定要求将棋盘覆盖住，就是棋盘的覆盖问题。

实际上，这里并不要求一定是某种棋盘，只要是有关覆盖若干行、若干列的方格网的问题，就是棋盘的覆盖问题。

（2）分类：棋盘的覆盖问题可以分为三类，一是能不能覆盖的问题，二是最多能用多少种图形覆盖的问题，三是有多少种不同的覆盖方法问题。

（3）重要结论：① m×n 棋盘能被2×1 骨牌覆盖的条件是m、n中至少有一个是偶数．② 2×n 的方格棋盘能用形骨牌覆盖的条件是3｜n．3、棋盘中的象棋问题：所谓棋盘，常见的有中国象棋棋盘（下图（1）），围棋盘（下图（2）），还有国际象棋棋盘（下图（3））．以这些棋盘为背景而提出的问题统称为棋盘问题。

这里面与数学推理、计算相关的棋盘问题，就叫做棋盘中的数学问题。

解决棋盘中的数学问题所使用的数学知识，统称棋盘中的数学。

1、利用卡片覆盖已知图形，掌握一是能不能覆盖的问题，二是最多能用多少种图形覆盖的问题，三是有多少种不同的覆盖方法问题；2、利用象棋知识寻找路线；例1 一种骨牌是由形如的一黑一白两个正方形组成，则下图中哪个棋盘不能用这种骨牌不重复地完全覆盖？（A）3×4 （B）3×5 （C）4×4（D）4×5 （E）6×3答案：通过试验，很容易看到，应选择答案（B）．分析：这类问题，容易更加一般化，即用2×1的方格骨牌去覆盖一个m×n的方格棋盘的问题．定理1： m×n棋盘能被2×1骨牌覆盖的充分且必要的条件是m、n中至少有一个是偶数．例2 下图中的8×8棋盘被剪去左上角与右下角的两个小方格，问能否用31个2×1的骨牌将这个剪残了的棋盘盖住？答案：我们将残角棋盘黑、白相间染色（如图），62个格中有黑格 32个，白格 30个．另外，如果用2×1骨牌 31张恰能盖住这个残角棋盘，我们发现，每个骨牌必定盖住一个黑格，一个白格，31个骨牌将盖住31个黑格及31个白格．这与32个黑格数，30个白格数的事实相矛盾．所以，无论如何用这31张2×1的骨牌盖不住这个残角棋盘．分析刚一想，31个2×1骨牌恰有62个小方格，棋盘去掉两个角后也是62个格，好像很有可能盖住．但只要简单一试，便发现不可能．仔细分析，发现如果把棋盘格黑、白相间染色后，2×1骨牌一次只能盖住一个黑格与一个白格．只要发现这个基本事实立即可以找到解答．例3 在下图（1）、（2）、（3）、（4）四个图形中：答案：图形（1）和（2）中各有11个方格，11不是3的倍数，因此不能用这两种图形拼成．图形来拼．只有图形（4）可以用这两种三个方格的图形来拼，具体拼法有多种，下图仅举出一种为例．分析：这道类型题用排除法，排除图（1）与（2）的方法是很重要的．因为一个图形可以用这是“必要条件排除法”．但要注意，一个图形小方格数是3的倍数，但是呢也不表明的就是这种情况．n|3。

五年级数学竞赛奥数讲义-例题一一、拓展提优试题1．如果2头牛可以换42只羊，3只羊可以换26只兔，2只兔可以换3只鸡，则3头牛可以换多少只鸡？2．若2副网球拍和7个网球一共220元，且1副网球拍比1个网球贵83元．求网球的单价．3．如图，在梯形ABCD中，若AB＝8，DC＝10，S△AMD＝10，S△BCM＝15，则梯形ABCD的面积是．4．李双骑车以320米分钟的速度从A地驶向B地，途中因自行车故障推车继续向前步行5分钟到距B地1800米的某地修车，15分钟后以原来骑车速度的1.5倍继续向前驶向B地，到达B地时，比预计时间多用17分钟，则李双推车步行的速度是米/分钟．5．如图，魔术师在一个转盘上的16个位置写下来了1﹣16共16个数，四名观众甲、乙、丙、丁参与魔术表演．魔术师闭上眼，然后甲从转盘中选一个数，乙、丙、丁按照顺时针方向依次选取下一个数，图示是一种可能的选取方式，魔术师睁开眼，说：“选到偶数的观众请举手．”，这时候，只有甲和丁举手，这时候魔术师就大喝一声：“我知道你们选的数了！”．你认为甲和丁选的数的乘积是．6．（8分）图中所示的图形是迎春小学数学兴趣小组的标志，其中，ABCDEF 是正六边形，面积为360，那么四边形AGDH的面积是．7．同时掷4个相同的小正方体（小正方体的六个面上分别写有数字1、2、3、4、5、6，则朝上一面的4个数字的和有种．8．某长方体的长、宽、高（长、宽、高均大于1）是三个彼此互质的自然数，若这个长方体的体积是665，则它的表面积是．9．如图：平行四边形ABCD中，OE＝EF＝FD．平行四边形面积是240平方厘米，阴影部分的面积是平方厘米．10．观察下表中的数的规律，可知第8行中，从左向右第5个数是．11．小明从家到学校去上课，如果每分钟走60米，可提前10分钟到校；如果每分钟走50米，要迟到4分钟到校．小明家到学校相距米．12．用一根34米长的绳子围成一个矩形，且矩形边长都是整数米，共有种不同的围法（边长相同的矩形算同一种围法）．13．如图，魔术师在一个转盘上的16个位置写下来了1﹣16共16个数，四名观众甲、乙、丙、丁参与魔术表演．魔术师闭上眼，然后甲从转盘中选一个数，乙、丙、丁按照顺时针方向依次选取下一个数，图示是一种可能的选取方式，魔术师睁开眼，说：“选到偶数的观众请举手．”，这时候，只有甲和丁举手，这时候魔术师就大喝一声：“我知道你们选的数了！”．你认为甲和丁选的数的乘积是．14．如图六角星的6个顶点恰好是一个正六边形的6个顶点，那么阴影部分面积是空白部分面积的倍．15．（8分）小胖把这个月的工资都用来买了一支股票．第一天该股票价格上涨，第二天下跌，第三天上涨，第四天下跌，此时他的股票价值刚好5000元，那么小胖这个月的工资是元．16．A、B两桶水同样重，若从A桶中倒2.5千克水到B桶中，则B桶中水的重量是A桶中水的重量的6倍，那么B桶中原来有水千克．17．如图是一个正方体的平面展开图，若该正方体相对的两个面上的数值相等，则a﹣b×c的值是．18．松鼠A、B、C共有松果若干，松鼠A原有松果26颗，从中拿出10颗平分给B、C，然后松鼠B拿出自己的18颗松果平均分给A、C，最后松鼠C把自己现有松果的一半平分给A、B，此时3只松鼠的松果数量相同，则松鼠C原有松果颗．19．（7分）对于a、b，定义运算“@”为：a@b＝（a+5）×b，若x@1.3＝11.05，则x＝．20．大于0的自然数n是3的倍数，3n是5的倍数，则n的最小值是．21．幼儿园给小朋友派礼物，如果有2人各派4个，其余各派3个，则还剩余11个，如果4人各派3个，其余各派6个，则剩余10个，问一共有多少件礼物？22．（12分）甲、乙两人从A地步行去B地．乙早上6：00出发，匀速步行前往；甲早上8：00才出发，也是匀速步行．甲的速度是乙的速度的2.5倍，但甲每行进半小时都需要休息半小时．甲出发后经过分钟才能追上乙．23．甲乙两人分别从AB两地同时出发相向而行，当甲走到一半时，乙将速度提高一倍，结果两人在距离B地1200米处相遇，并且最后同时到达，那么两地相距米24．由120个棱长为1的正方体，拼成一个长方体，表面全部涂色，只有一面染色的小正方体，最多有块25．（7分）爱尔兰作家刘易斯曾写过一篇反讽寓言，文中描述了一个名为尼亚特泊的野蛮国家．在这个国家里使用西巴巴数字．西巴巴数字的形状与通用的阿拉伯数字相同，但含义相反．如“0”表示“9”，“1”表示“8”，以次类推．他们写数字是从左到右，使用的运算符号也与我们使用的一样．例如，他们用62代表我们所写的37．按照尼亚特泊人的习惯，应怎样写837+742的和是419．【分析】“0”表示“9”，0+9＝9，“1”表示“8”，1+8＝9，由此可知西巴巴数字，表示的数字与正常数字的和都是9；由此找出837、742表示的数字，然后相加即可．26．（7分）后羿朝三个箭靶分别射了三支箭，如图：他在第一个箭靶上得了29分，第二个箭靶上得了43分．请问他在第三个箭靶上得了分．27．有一行数：1，1，2，3，5，8，13，21，…，从第三个数开始，每个数都是前两个数的和，问在前2007个数中，有是偶数．28．（7分）今年小翔和爸爸、妈妈的年龄分别是5岁、48岁、42岁．年后爸爸、妈妈的年龄和是小翔的6倍．29．将100按“加15，减12，加3，加15，减12，加3，…”的顺序不断重复运算，运算26步后，得到的结果是．（1步指每“加”或“减”一个数）30．（7分）棱长都是1厘米的63个白色小正方体和1个黑色小正方体，可以拼成一个大正方体，问：一共可以拼成种不同的含有64个小正方体的大正方体．31．如图，在等腰直角三角形ABC中，斜边AB上有一点D，已知CD＝5，BD 比AD长2，那么三角形ABC的面积是．32．如图，从A到B，有条不同的路线．（不能重复经过同一个点）33．数学家维纳是控制论的创始人．在他获得哈佛大学博士学位的授予仪式上，有人看他一脸稚气的样子，好奇地询问他的年龄．维纳的回答很有趣，他说：“我的年龄的立方是一个四位数，年龄的四次方是一个六位数，这两个数刚好把0﹣9这10个数字全都用上了，不重也不漏，”那么，维纳这一年岁，（注：数a的立方等于a×a×a，数a的四次方等于a×a×a×a）34．鸡与兔共100只，鸡的脚比兔的脚多26只．那么，鸡有只．35．小松鼠储藏了一些松果过冬．小松鼠原计划每天吃6个松果，实际每天比原计划多吃2个，结果提前5天吃完了松果．小松鼠一共储藏了个松果．36．商店对某饮料推出“第二杯半价”的促销办法．那么，若购买两杯这种饮料，相当于在原价的基础上打折．37．甲、乙两车从A城市出发驶向距离300千米远的B城市．已知甲车比乙车晚出发1小时，但提前1小时到达B城市．那么，甲车在距离B城市千米处追上乙车．38．已知一个五位回文数等于45与一个四位回文数的乘积（即＝45×），那么这个五位回文数最大的可能值是59895．39．小胖和小亚两人在生日都是在五月份，而且都是星期三．小胖的生日晚，又知两人的生日日期之和是38，小胖的生日是5月日．40．用1，2，3，4，5，6，7，8这八个数字组成两个不同的四位数（每个数字只用一次）使他们的差最小，那么这个差是．【参考答案】一、拓展提优试题1．解：42÷2＝21（只）21÷3×26＝7×26＝182（只）182÷2×3＝91×3＝273（只）273×3＝819（只）答：3头牛可以换819只鸡． 2．解：220﹣83×2 ＝220﹣166 ＝54（元） 54÷（2+7） ＝54÷9 ＝6（元）答：网球每个6元．3．解：△ADM 、△BCM 、△ABM 都等高， 所以S △ABM ：（S △ADM +S △BCM ）＝8：10＝4：5， 已知S △AMD ＝10，S △BCM ＝15，所以S △ABM 的面积是：（10+15）×＝20， 梯形ABCD 的面积是：10+15+20＝45； 答：梯形ABCD 的面积是45． 故答案为：45．4．解：1800÷320﹣1800÷（320×1.5） ＝5.625﹣3.75 ＝1.875（分钟）320×[5﹣（17﹣15+1.875）]÷5 ＝320×[5﹣3.875]÷5 ＝320×1.125÷5 ＝360÷5 ＝72（米/分钟）答：李双推车步行的速度是72米/分钟． 故答案为：72． 5．解：依题意可知：2个偶数中间间隔是2个奇数．发现只有数字10，11，9，12是符合条件的数字． 乘积为10×12＝120． 故答案为：1206．解：根据分析，（1）△ABC 面积等于六边形面积的，连接AD ， 四边形ABCD 是正六边形面积的，故△ACD 面积为正六边形面积的 （2）S △ABC ：S △ACD ＝1：2，根据风筝模型，BG ：GD ＝1：2；（3）S△BGC：S CGD＝BG：GD＝1：2，故；故AGDH面积＝六边形总面积﹣（S△ABC +S△CGD）×2＝360﹣（+40）×2＝160．故答案是：1607．解：根据分析可得，朝上一面的4个数字的和最小是：1×4＝4，最大是6×4＝24，24﹣4+1＝21（种）答：朝上一面的4个数字的和有 21种．故答案为：21．8．解：665＝19×7×5，因为长、宽、高（长、宽、高均大于1）是三个彼此互质的自然数，所以长、宽、高分别是19、7、5，（19×7+19×5+7×5）×2＝（133+95+35）×2＝263×2＝526，答：它的表面积是526．故答案为：526．9．解：因为平行四边形ABCD中，AC和BD是对角线，把平行四边形ABCD 的面积平分4份，平行四边形面积是240平方厘米，所以S△DOC＝240÷4＝60（平方厘米），又因为△OCE、△ECF、△FCD和△DOC等高，OE＝EF＝FD，所以S△ECF＝S△DOC＝×60＝20（平方厘米），所以阴影部分的面积是 20平方厘米．故答案为：20．10．解：由图可知，第1行的数为1，第2行的最后一个数为2×2＝4，第3行的最后一个数为3×3＝9，…所以第7行最后一个数为7×7＝49，则第8行第1个数为49+1＝50，第5个数为50+4＝54，故答案为：54．11．解：（60×10+50×4）÷（60﹣50），＝（600+200）÷10，＝800÷10，＝80（分钟），60×（80﹣10），＝60×70，＝4200（米）．答：小明家到学校相距4200米．故答案为：4200．12．解：设矩形的长为am，宽为bm，且a≥b，根据题意，a+b＝17，由于a，b均为整数，因此（a，b）的取值有以下8种：（16，1），（15，2），（14，3），（13，4），（12，5），（11，6），（10，7），（9，8），故答案为8．13．解：依题意可知：2个偶数中间间隔是2个奇数．发现只有数字10，11，9，12是符合条件的数字．乘积为10×12＝120．故答案为：12014．解：根据分析，如图所示，将图进行分割成面积相等的三角形，阴影部分由18个小三角形组成，而空白部分有6个小三角形，故阴影部分面积是空白部分面积的18÷6＝3倍．故答案是：3．15．解：5000÷（1﹣）÷（1+）÷（1﹣）÷（1+）＝5000××××＝5000（元）答：小胖这个月的工资是5000元．故答案为：5000．16．解：2.5×2÷（6﹣1）+2.5＝5÷5+2.5＝1+2.5＝3.5（千克）答：B桶中原来有水3.5千克．故答案为：3.5．17．解：依题意可知：3a+2与17是对立面，3a+2＝17，所以a＝5；7b﹣4与10是对立面，7b﹣4＝10，所以b＝2；a+3b﹣2c与11的对立面，5+3×2﹣2c＝11，所以c＝0；所以a﹣b×c＝5故答案为：518．解：10÷2＝5（颗）18÷2＝9（颗）此时A有：26﹣10+9＝25（颗）此时C有：25×4＝100（颗）原来C有：100﹣9﹣5＝86（颗）答：松鼠C原有松果 86颗．故答案为：86．19．解：由定义可知：x@1.3＝11.05，（x+5）1.3＝11.05，x+5＝8.5，x＝8.5﹣5＝3.5故答案为：3.520．解：3n是5的倍数，3n的个数一定是0或5又因为大于0的自然数n是3的倍数，所以3n最小是453n＝45n＝15所以n最小取15时，n是3的倍数，3n是5的倍数．答：n的最小值是15．故答案为：15．21．【分析】假设第一次每人都派3个，则还剩余2×（4﹣3）+11＝13个，第二次如每人都派6个，同时少了4×（6﹣3）﹣10＝2个，就是每人多派6﹣3＝3个，则需要13+2＝15个礼物，据此可求出人数，进而可求出礼物数．解：[2×（4﹣3）+11+4×（6﹣3）﹣10]÷（6﹣3）＝[2×1+11+4×3﹣10]÷3＝[2+11+12﹣10]÷3＝15÷3＝5（人）2×4+（5﹣2）×3+11＝8+3×3+11＝8+9+11＝28（件）答：一共有28件礼物．22．解：法一：假设甲一小时走5米，乙一小时走2米，列表如下：时间甲（米）乙（米）时间甲（米）乙（米）0小时043小时7.5100.5小时 2.55 3.5小时10111小时 2.564小时10121.5小时57 4.5小时12.5132小时585小时12.5142.5小时7.59 5.5小时1515观察得5.5小时恰好追上（如果这时间超过了乙，就要用具体追及公式计算追及时间）法二：也可以设甲的速度为每小时10a（甲要休息，实际每小时走5a），乙的速度为每小时4a，因此要追8a．半小时内最多追3a，可以先从要追的8a中扣除3a，因为在此之前不可能追上（之前的距离差不止3a）．之后再开始按每半小时列出，若不够半小时的话，用追及公式算．前面追的5a，相当于每小时追a，可以用5a÷（5a﹣4a）＝5（小时）计算．之后，甲半小时再走2a，乙再走5a，加上还差的3a，正好追上．因此，要追5.5小时，即330分钟．故答案为：330．23．2800[解答] 设两地之间距离为S 。

第15讲长方体和正方体(三)一、知识要点解答有关长方体和正方体的拼、切问题，除了要切实掌握长方体、正方体的特征，熟悉计算方法，仔细分析每一步操作后表面几何体积的等比情况外，还必须知道：把一个长方体或正方体沿水平方向或垂直方向切割成两部分，新增加的表面积等于切面面积的两倍。

二、精讲精练【例题1】一个棱长为6厘米的正方体木块，如果把它锯成棱长为2厘米的正方体若干块，表面积增加多少平方厘米？练习1：1.把27块棱长是1厘米的小正方体堆成一个大正方体，这个大正方体的表面积比原来所有的小正方体的表面积之和少多少平方厘米？2.有一个棱长是1米的正方体木块，如果把它锯成体积相等的8个小正方体，表面积增加多少平方米？【例题2】有一个正方体木块，把它分成两个长方体后，表面积增加了24平方厘米，这个正方体木块原来的表面积是多少平方厘米？练习2：1.把三个棱长都是2厘米的正方体拼成一个长方体，这个长方体的表面积是多少平方厘米？2.有一个正方体木块，长4分米、宽3分米、高6分米，现在把它锯成两个长方体，表面积最多增加多少平方分米？【例题3】有一个正方体，棱长是3分米。

如果按下图把它切成棱长是1分米的小正方体，这些小正方体的表面积的和是多少？练习3：1.用棱长是1厘米的小正方体摆成一个稍大一些的正方体，至少需要多少个小正方体？如果要摆一个棱长是6厘米的正方体，需要多少个小正方体？2.有一个长方体，长10厘米、宽6厘米、高4厘米，如果把它锯成棱长是1厘米的小正方体，一共能锯多少个？这些小正方体的表面积和是多少？【例题4】一个正方体的表面涂满了红色，然后如下图切开，切开的小正方体中：（1）三个面涂有红色的有几个？（2）二个面涂有红色的有几个？（3）一个面涂有红色的有几个？（4）六个面都没有涂色的有几个？1.把一个棱长是5厘米的正方体的六个面涂满红色，然后切成1立方厘米的小正方体，这些小正方体中，一面涂红色的、二面涂红色的、三面涂红色的以及六个面都没有涂色的各有多少个？2.把若干个体积相同的小正方体堆成一个大的正方体，然后在大正方体的表面涂上颜色，已知两面被涂上红色的小正方体共有24个，那么，这些小正方体一共有多少个？【例题5】一个长方体的长、宽、高分别是6厘米、5厘米和4厘米，若把它切割成三个体积相等的小长方体，这三个小长方体表面积的和最大是多少平方厘米？1.有三块完全一样的长方体木块，每块长8厘米、宽5厘米、高3厘米。

“包含与排除” 学生姓名授课日期 教师姓名授课时长包含与排除是小学奥数中一个非常重要的知识点，很多杯赛和小升初选拔考试中都会有相关考察内容，是考察学生逻辑思维能力，以及理解利用新知识的一个非常重要的方面，其中容斥原理更是最关键的点，而且与数论和几何的综合性题目是历年考察的重点。

一、容斥原理公式1、若已知A 、B 、C 三部分的数量（如图），其中C 为重复部分，则图中的数量等于A+B-C. 即：A ∪B=A+B- A ∩B ，其中A ∩B=C.2、若已知A 、B 、C 三部分的数量（如图）， 则图中的数量等于A+B+C-（A 与B 重叠部分+ B 与C 重叠部分+ C 与A 重叠部分）+A 、B 、C 三者重叠的部分.即：A ∪B ∪C=A+B+C-（A ∩B+B ∩C+C ∩A ）+ A ∩B ∩C.以上概念中符号解释：“∪”表示并集，“A ∪B ”表示A 并B ，通俗的讲表示所有或属于A 、或属于B 的元素的数量（集合），“A ∪B ∪C ” 通俗的讲表示所有或属于A 、或属于B 、或属于C 的元素数量.“∩”表示交集，“A ∪B ”表示A 交B ，通俗的讲表示所有即属于A 、又属于B 的元素的数量（集合），“A ∩B ∩C ”通俗的讲表示所有即属于A ，又属于B ，还属于C 的元素数量C B A C B A【试题来源】【题目】某小学三年级四班，参加语文兴趣小组的有28人，参加数学兴趣小组的有29人，有12人两个小组都参加。

这个班有多少人参加了语文或数学兴趣小组？【试题来源】【题目】在桌面上放置着三个两两重叠的圆纸片（如图，三个圆等大），它们的面积都是100cm2，并知A、B两圆重叠的面积是20cm2，A、C两圆重叠的面积为45cm2，B、C两圆重叠的面积为31cm2,三个圆共同重叠的面积为15cm2，求盖住桌子的总面积。

【试题来源】【题目】东方大学有外语老师120名，其中教英语的有50名，教日语的45名，教法语的有40名，有15名教师既教英语又教日语，有10名教师既教英语又教法语，有8名教师既教日语又教法语，有4名教师会教英语、日语和法语三门课，求不教这三门课的外教有多少名？【试题来源】【题目】五年级三班有46名学生参加三项课外活动，其中24人参加了绘画小组，20人参加了合唱小组，参加朗诵小组的人数是既参加绘画小组又参加朗诵小组人数的3.5倍，又是三项活动都参加人数的7倍，既参加朗诵小组又参加合唱小组的人数相当于三项都参加人数的2倍，既参加绘画小组又参加合唱小组的有10人，求参加朗诵小组的人数。

所谓操作问题，实际上是对某个事物按一定要求进行的一种变换，这种变换可以具体执行。

例如，对任意一个自然数，是奇数就加1，是偶数就除以2。

这就是一次操作，是可以具体执行的。

操作问题往往是求连续进行这种操作后可能得到的结果。

实际操作与策略问题这类题目能够很好的提高学生思考问题的能力，激发学生探索数学规律的兴趣，并通过寻找最佳策略过程，培养学生的创造性思维能力，这也是各类考试命题者青睐的这类题目的原因。

【例1】★（《小数报》数学竞赛初赛应用题第2题）锻工师傅收到五段铁链，每段有三个环（如图）要求连成一条铁链，你认为至少打开几个环，才能连成一条铁链？【解析】 至少打开3个环，因为打开2个环，只能连结三段铁链，而将一段铁链的3个环全打开，就可以将其余四段全连结起来。

【例2】★有个吝啬的老财主，总是不想付钱给长工。

这一次，拖了一个月的工钱，还是不想付。

可是不付又说不过去，便故作大方地拿出一条金链，共有7环。

对长工说：“我不是要拖欠工资，只是想连这一个月加上再做半年的工资，都以这根金链来付。

”他望向吃惊的长工，心中很是得意，“本人说话，从不食言，可以请大老爷作证。

”大老爷可是说一不二的人，谁请他作证，他当作一种荣耀，总是分文不取，并会以命相拼也要兑现的。

这越发让长工不敢相信，要知道，这在以往，这样的金链中的一环三个月的工钱也不止。

老财主典型例题知识梳理越发得意，终于拿出杀手锏：“不过，我请大老爷作证的时候，提到一项附加条件，就是这样的金链实在不能都把它断开，请你只能打开一环，以后按月来取才行！”当长工明白了老财主的要求后，不仅不为难，反倒爽快地答应了，而且，从第一个月到第七个月，顺利地拿到了这条金链，你知道怎么断开这条金链吗？【解析】断开第三环，从而得到1，2，4环的三段，第一个月拿走一环，第二个月以一换二，第三个月再取一环，第四个月以三换四，第五个月再取一环，第六个月以一换二，第七个月再取一环。

【例3】★★有一堆棋子共有2002粒，甲、乙两人玩轮流取棋子的游戏。