当前位置：文档之家 › 132画轴对称图形第2课时精品PPT课件

132画轴对称图形第2课时精品PPT课件

  • 格式：pptx
  • 大小：4.17 MB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

人教版八年级数学上册：13.2画轴对称图形(第二课时)ppt课件

人教版八年级数学上册：13.2画轴对称图形(第二课时)ppt课件

， 2
(2)△OAB的面积等于
．
9．如图，△ABC在平面直角坐标系中，其中点A、B、 C的坐标分别为A(-2，1)，B(-4，5)，C(-5，2)．
(1)作△ABC关于直线l：x=-1对称的△A1B1C1，其中， 点A、B、C的对称点分别为点A1、B1、C1；
(2)写△出A1B1C1的坐标．
解：(1)△A1B1C1如下图． (2)A1(0，1)，B1(2，5)， C1(3，2)．
+(b+4) 2=0，那么点M(a，b)关于y轴的
对称点的坐标(-为3，-4)
．
8．如图，知△OAB关于x轴对称． (1)点A的坐标为(1，-2)，那么点B的坐标为(1，2)
．
假设△OAB关于y轴对称的图形是△O1A1B1,那么
△O1A(01，B10)
(-1，-2)
O1 (-1，2) ，A1
B1
;
【提示】首先由正方形ABCD中，顶点A(1，3)、B(1， 1)、C(3，1)，求得点M的坐标为(2，2)，然后根据题 意求得第1次、2次、3次变换后的对角线交点M的对应 点的坐标，即可得规律：当n为奇数时， M的坐标为(2-n，-2)，当n为偶数时，M的坐标为 (2-n，2)．故当n=2019时，M的坐标为 (-2019，-2) ．
6．一只电子跳蚤从点A(1，-2)开场，先以x轴为对称轴 跳至点B，紧接着又以y轴为对称轴跳至点C，那么点C 的坐标为(-1，2) ．
7．(1)点(-4，b)与点(a-1，-3)关于y轴对称，那么a=5 ， b= -3 ;
(2)知点A(a，-3)与B( ，b)关于x轴对称，那么a+b=
;
(3)假设
10．如图，在边长为1个单位长度的小正方形组成的坐标系网格 中，点A、B、C都是格点． (1)画出△ABC关于x轴对称的△A1B1C1； (2)将△A1B1C1向左平移7个单位，得到△A2B2C2，请画出 △A2B2C2； (3)知△ABC的边AC上有一点D(m，n)， 求点D在(1)(2)中的两次操作后对应 △A2B2C2的点E坐标．

13.2 第2课时 用坐标表示轴对称

13.2 第2课时 用坐标表示轴对称

拓展提升
9.在平面直角坐标系中，规定把一 个正方形先沿着x轴翻折，再向右 平移2个单位称为1次变换．如图， 已知正方形ABCD的顶点A、B的坐 标分别是（-1，-1）、（-3，-1）， 把正方形ABCD经过连续7次这样的 变换得到正方形A′B′C′D′，求B的 对应点B′的坐标.
解：∵正方形ABCD，点A、B的坐标分别是(-1，-1)、(-3，-1)， ∴根据题意，得第1次变换后的点B的对应点的坐标为(-3+2，1)， 即(-1，1)， 第2次变换后的点B的对应点的坐标为(-1+2，-1)，即(1，-1)， 第3次变换后的点B的对应点的坐标为(1+2，1)，即(3，1)， 第n次变换后的点B的对应点的为：当n为奇数时为(2n-3，1)，当 n为偶数时为(2n-3，-1)， ∴把正方形ABCD经过连续7次这样的变换得到正方形A′B′C′D′， 则点B的对应点B′的坐标是(11，1)．
解得a＝－8，b＝－5；
称的点的特征列方
(2)∵A、B关于y轴对称，
程(组)求解．
∴2a－b＋2b－1＝0，5＋a＝－a＋b，
解得a＝－1，b＝3，
∴(4a＋b)2016＝1.
例3 已知点P(a＋1，2a－1)关于x轴的对称点在第一
象限，求a的取值范围．
解：依题意得P点在第四象限，
a+1＞0 2a 1＜0.
（简称：纵轴纵相等） 练一练: 1.点P(-5, 6)与点Q关于y轴对称，则点Q的坐标为 __(_5_,__6_)___. 2.点M(a, -5)与点N(-2, b)关于y轴对称，则a=__2___, b =__-_5__.
例1 如图，四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),

八年级数学上册 13.2.2 用坐标表示轴对称习题课件 (新版)新人教版

八年级数学上册 13.2.2 用坐标表示轴对称习题课件 (新版)新人教版

14．在如图的正方形网格中，每个小正方形边长为1，格点三角形(顶点 是网格线的交点的三角形)ABC的顶点A，C的坐标分别为(－4，5)，(－ 1，3)． (1)请在如图的网格平面内作出平面直角坐标系； (2)请作出△ABC关于y轴对称的△A′B′C′； (3)写出点B′的坐标．
解：(1)图略 (2)图略 (3)B′(2，1)
解：(1)A1(0，4)，B1(2，2)，C1(1，1)，图略 (2)A2(6，4)，B2(4，2)，C2(5，1)，图略 (3)△A1B1C1与△A2B2C2关于直线x＝3对称，图略
16．如图，在平面直角坐标系中，l是第一、三象限的角平分线．
(1)试验与探究： 由图观察易知A(0，2)关于直线l的对称点A′的坐 标为(2，0)，请在图中分别标明B(5，3)，C(－2 ， 它5们)关的于坐直标线：lB的′_对__称__点__B，′，(3C，C′_′5的_)_位__置__，_．并写出 (2)归(5纳，与－发2)现： 结合图形观察以上三组点的坐标，你会发现： 坐标平面内任一点P(m，n)关于第一、三象限的 角平分线l的对称点P′的坐标为___(_n_，__m__) _． 解：图略
方法技能： 1．关于坐标轴对称的点的坐标特征： (1)点(x，y)关于x轴对称的点的坐标为(x，－y)，即横坐标相等， 纵坐标互为相反数； (2)点(x，y)关于y轴对称的点的坐标为(－x，y)，即横坐标互为 相反数，纵坐标相等． 2．作一个多边形关于坐标轴对称的图形，只需作出多边形各个 顶点关于坐标轴的对称点，并顺次连接这些点即可． 易错提示： 混淆关于x轴和y轴对称的点的横、纵坐标的变化特征而出错．
B ) A．A点 B．B点 C．C点 D．D点
12．如图，以长方形ABCD的中心为原点建立直角坐标系，点A的坐标 是(3，2)，则点B的坐标是_(_3_，__－__2_)，点C的坐标是__(－__3_，__－__2_)__，点D 的坐标是__(－__3_，__2_)_．

数学上册132画轴对称图形第2课时课件新版新人教

数学上册132画轴对称图形第2课时课件新版新人教

04 练习与巩固
基础练习题
总结词
针对轴对称图形的基本概念和性质进行练习，旨在帮助学生掌握基础知识。
正方形
是，对称轴为两条对角线。
基础练习题
等边三角形
是，对称轴为三条中垂线。
圆形
是，对称轴为任意直径。
基础练习题
点A(2,3)关于x轴的 对称点是A'(2,-3)。
3. 根据轴对称性质， 计算下列图形的面积 。
建筑美学
轴对称图形广泛应用于建筑设计中，如对称的建筑立面、布局等，给人以平衡 、稳定和美观的视觉效果。
自然界中的轴对称
自然界中许多物体呈现轴对称形态，如蝴蝶、花朵、蜂巢等，这种对称性在生 物学和生态学中具有重要应用。
轴对称图形在数学中的运用
几何学研究
轴对称图形是几何学研究的重要内容，对于理解几何图形的性质、分类和变换具 有重要意义。
检查对称性
检查绘制的图形是 否符合轴对称性质 。
画轴对称图形的注意事项
对称轴的选择
选择合适的对称轴，确保 图形具有对称性。
细节的处理
在绘制过程中，注意细节 的处理，确保图形的准确 性。
保持对称性
在完成图形后，检查其是 否具有对称性，并做相应 调整。
03 轴对称图形的应用
轴对称图形在生活中的运用
轴对称
如果一个图形关于某条直线对称 ，那么这个图形叫做轴对称图形 ，这条直线叫做对称轴。
轴对称图形的性质
对称性
轴对称图形具有对称性，即图形 关于对称轴对称。
稳定性
轴对称图形具有稳定性，即图形在 折叠时不会改变其形状和大小。
唯一性
对于一个轴对称图形，其对称Hale Waihona Puke 是 唯一的。轴对称图形的分类

13.2 画轴对称图形第2课时

13.2 画轴对称图形第2课时

B
1
D
1
O B′
D′ A
E x E′
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
在平面直角坐标系中，画出下列已知点及其关于 y 轴对称的点，把它们的坐标填入表格中．
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
y B B〞 1 D〞 D E〞 O 1 C A〞 A
E
x
C〞
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
如图，如果以天安门为原点，分别以长安街和中 轴线为x轴和y 轴建立平面直角坐标系，对应于东直门 的坐标，你能找到西直门 的位置，说出西直门的坐 标吗？
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
对于平面直角坐标系中任意一点，你能找出其关于 x 轴或y 轴对称的点的坐标吗？它们之间有什么规律？
解：关于x 轴对称的点的坐标：（-2， -6）， （1，2），（-1， -3），（-4，2），（1，0） ． 关于y 轴对称的点的坐标：（2，6）， （-1，-2），（1，3），（4，-2），（-1，0） ．
课堂练习
练习2 若点P（2a+b，-3a）与点P′（8，b+2） 2 ，b= 4 ；若关于y 轴对 关于x 轴对称，则a = -20 6 ，b=______. 称，则a =
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
在平面直角坐标系中，画出下列已知点及其关 于x 轴对称的点，把它们的坐标填入表格中．
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
y
C′ A′
B
1
D
1
O B′ C
D′ A

《画轴对称图形》轴对称PPT教学课件(第2课时)

《画轴对称图形》轴对称PPT教学课件(第2课时)

巩固练习
平面直角坐标系中，△ABC的三个顶点坐标分别为A（0,4）， B（2,4），C（3，–1）. （1）试在平面直角坐标系中，标出A、B、C三点； （2）若△ABC与△A'B'C'关于x轴对称，画出△A'B'C'，并 写出A'、B'、C'的坐标.
巩固练习 解：如图所示：
y
A (0,4)
B (2,4)
4.如图，在平面直角坐标系中，点P（–1，2）关于直线x=1的
对称点的坐标为（ C ）
A．（1，2） B．（2，2）
1 2
C．（3，2） D．（4，2）
-1
1
课堂检测 5.已知点P(2a+b,–3a)与点P′（8,b+2). 若点P与点P′关于x轴对称，则a=___2__， b=____4___. 若点P与点P′关于y轴对称，则a=___6__ ，b=___–_2_0__.
课堂检测
解：∵正方形ABCD，点A、B的坐标分别是(–1，–1)、(–3，–1)， ∴根据题意，得第1次变换后的点B的对应点的坐标为(–3+2，1)，即(–1，1)， 第2次变换后的点B的对应点的坐标为(–1+2，–1)，即(1，–1)， 第3次变换后的点B的对应点的坐标为(1+2，1)，即(3，1)， 第n次变换后的点B的对应点的为：当n为奇数时为(2n–3，1)，当n为偶数时为 (2n–3，–1)， ∴把正方形ABCD经过连续7次这样的变换得到正方形A′B′C′D′，则点B的对应 点B′的坐标是(11，1)．
D．（–1，–4）
课堂检测
基础巩固题
1.平面直角坐标系内的点A（–1，2）与点B（–1，–2）关于（ B ）

13.2画轴对称图形(第2课时)课件ppt

谢谢观赏
You made my day!
我们，还在路上……
八年级 上册
13.2 画轴对称图形 （第2课时）
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
如图，如果以天安门为原点，分别以长安街和中 轴线为x轴和y 轴建立平面直角坐标系，对应于东直门 的坐标，你能找到西直门 的位置，说出西直门的坐 标吗？
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
解：关于x 轴对称的点的坐标：（-2， -6）， （1，2），（-1， -3），（-4，2），（1，0） ．
关于y 轴对称的点的坐标：（2，6）， （-1，-2），（1，3），（4，-2），（-1，0） ．
课堂练习
练习2 若点P（2a+b，-3a）与点P′（8，b+2） 关于x 轴对称，则a = 2 ，b= 4 ；若关于y 轴对 称，则a = 6 ，b=__-_2_0__.
O
1
D′
E E′
x
B′
C
A
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
观察下图中关于x 轴对称的每对对称点的坐标有怎
样的变化规律？
y
C′ 关于x 轴对称的每对对 称点的横坐标相等，纵坐标 互为相反数．
C
A′ B
1D
O
1
D′
B′
A
E E′
x
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
在平面直角坐标系中，画出下列已知点及其关于 y 轴对称的点，把它们的坐标填入表格中．
C y C′
D
D′
为： A′（ 5 ， 1 ）， B′（ 2 ， 1 ），
A
B
1
O

人教版八年级数学上册作业课件：13.2 画轴对称图形 第2课时 用坐标表示轴对称 (共23张PPT)


C．点(3，4)与点(3，－4)关于x轴对称
D．点(4，－3)与点(4，3)关于y轴对称
3 ． 在 平 面 直 角 坐 标 系 中 ， 点 ( － 3 ， 2) 关 于 y 轴 的 对 称 点 的 坐 标 是 ____(_3_，__2_) __． 4．(2017·南京模拟)在平面直角坐标系中，点A的坐标(2，－3)，作点A 关于x轴的对称点，得到点A′，再作点A′关于y轴的对称点，得到点A″， 则点A″的坐标是_________(_－．2，3)
(1)若点 M 的坐标为(x，y)，则经过这种变换后的对应点 N 的坐标为 ___(_－__x_，__y_)； (2)经过这种变换后，点 P 的对应点为 Q，若 P(－2，a)，Q(b，3)，试求 代数式a1b＋（a＋1）1（b＋1）＋…＋（a＋2017）1（b＋2017）的值．
解 ： 由 (1) 得
9．(2016·宁夏)如图，在平面直角坐标系中，△ABC的三个顶点坐标分 别为A(－2，1)，B(－4，5)，C(－5，2)． (1)画出△ABC关于y轴对称的△A1B1C1； (2)画出△A1B1C1关于x轴对称的△A2B2C2.
解：(1)△A1B1C1如图所示 (2)△A2B2C2如图所示
10．坐标平面内的点A(－1，2)和B(－1，6)关于某条直线对称，则对称 轴是( C)
解：(1)△A1B1C1如图所示 (2)∵△ABC向右平移6个单位，∴A，B，C三点的横坐标加6，纵坐标不 变，作出△A2B2C2如图所示，A2(6，4)，B2(4，2)，C2(5，1)
(3)△A1B1C1和△A2B2C2关于图中直线l：x＝3对称
15．如图，△COB 是由△AOB 经过某种变换后得到的图形，观察点 A 与点 C 的坐标之间的关系，解答下列问题：

3.2画轴对称图形第2课时用坐标表示轴对称课件(新人教版)_1_6-10

杨伯家的一只竹背篓据说有250余年历史了。，” 老先生响应：“别担心，你只管全力以赴，我有我的安排与方法
C (3,-4)
知识归纳
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
（简称：横轴横相等） 练一练: 1.点P(-5, 6)与点Q关于x轴对称，则点Q的坐标为___(-_5__,_-_6__) . 2.点M(a, -5)与点N(-2, b)关于x轴对称，则a=_-_2___, b =___5__.
问题2：如图，在平面直角坐标系中你能画出点A关于x轴的对 称点吗?
y
A (2,3)
你能说出点A与点 A'坐标的关系吗？
O
x
A′(2,-3)
做一做：在平面直角坐标系中画出下列各点关于x轴的对称点.
y
(x-4,2)
O
C '(3,4)
x
( x , -y)
B '(-4,-2)
C (3,-4)
老虎看着走在前面的上帝，越看越不顺眼，几欲偷袭扑杀，无奈胜算不大心存恐惧，只好忍气吞声忍辱负重。老渔夫问他为什么要走上绝路，他说自己得不到别人和社会的承认，没有人欣赏并且重用他，他无颜再见 江东父老。你能教我这门游泳技术吗?”
“行呀，凭我的本事肯定教你成为泳界高手，”鸭子回答得挺自信：“可是公鸡大哥，倒是你啼鸣报晓引吭高歌的技能挺专业，还能时常得到主人谷米的奖赏，我太感兴趣了，你能教我这门技术吗?” “这不成问题呀，小事一桩。 人工晶体植入术价格 https:///lens-surgeries/costs/ ”村长说。
问题3：如图，在平面直角坐标系中你能画出点A关于y轴的对 称点吗?
y
A′(-2,3)
A (2,3)

最新人教部编版八年级数学上册《13.2画轴对称图形【全套】》精品PPT优质课件


-2 -3
12
y
6 -5
1 1
2
-4 0
B B〞
E〞 D〞1 D E O1
x
C
A〞 A
C〞
观察关于y 轴对称的每对对称点的坐标
有怎样的变化规律？
y
关于y 轴对称的 每对对称点的横坐 标互为相反数，纵 坐标相等．
B B〞
E〞 D〞1 D E O1
x
C
A〞 A
C〞
再找几个点，分别画出它们的 对称点，检验一下你发现的规律．
23
-1 -2
y
-6 5
1 2
-1
40
C′
A′
B
1D
O
1
D′
E E′
x
B′
C
A
观察下图中关于x 轴对称的每对对称点 的坐标有怎样的变化规律？ y
C′ 关于x 轴对称的
A′ B
每对对称点的横坐标 相等，纵坐标互为相 反数．
C
1D
O
1
D′
B′
A
E E′
x
在平面直角坐标系中，画出下列已知 点及其关于y 轴的对称点，把它们的坐标 填入表格中．
思考
如果有一个图形和一条直线，如何画 出这个图形关于这条直线对称的图形呢？
例1 如图，已知△ABC 和直线l，画出与 △ABC关于直线l 对称的图形． B
C A
l
画法：（1）如图，过点A 画直
线l 的垂线，垂足为点O，在垂线上 B
截取OA′=OA，点A′就是点A 关
C
于直线l 的对称点；
A
（2）同理，分别画点B，C 关 O
谢谢观赏！
再见！
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

你能说出
-2
点A与点 A′坐标的
-3
关系吗？
-4
在平面直角坐标系中画出下列各点关于
y轴的对称点.
y
5 4
· B (-4, 2) 3 2
1
关于y轴对 称的点的
B′ (4, 2)
· 坐标具有 怎样的关
-4 -3 -2 -1O-1
-2 -3
· -4
C′(-3, -4)
1 2 3 4 5 x 系？
·C(3, -4)
y
【解析】点A(-3,5), B(-4,1),C(-1,3)，关于 y轴对称点的坐标分别为 A′(3,5),B′(4,1), C′(1,3).依次连接 A′B′,B′C′,
· A
5
·A′
· · C4 3 C′
·2
B
1
·B′
-4 -3 -2 -1-O1 1 2 3 4 5 x
C′A′,就得到△ABC关于y轴
关于y轴对称的点的横坐标互为相反数, 纵坐标 相等.
点（x, y）关于x轴对称的点的坐标为_(_x_,_－__y_)_. 点（x, y）关于y轴对称的点的坐标为_(_－__x_,_y_)_.
【例题】
已知△ABC的三个顶点的坐标分别为A(-3，5),B(-4，1),
C(-1，3)，作出△ABC关于y轴对称的图形.
的坐标是多少?
(-x+2,y)
（2）在平面直角坐标系中,点(x,y)关于直线x=-1对称点
的坐标是多少?
(-x-2,y)
（3）在平面直角坐标系中,点(x,y)关于直线y=1对称点
的坐标是多少?
(x,-y+2)
（4）在平面直角坐标系中,点(x,y)关于直线y=-1对称点
的坐标是多少? (x,-y-2)
B′ (-4, -2) -3
-4
· C′(3, 4) 关于x轴对称的点的横坐标 相同，纵坐标互为相反数. 12345 x
· C(3, -4)
y
5
· A′ (-2,3)
4 3
2
1
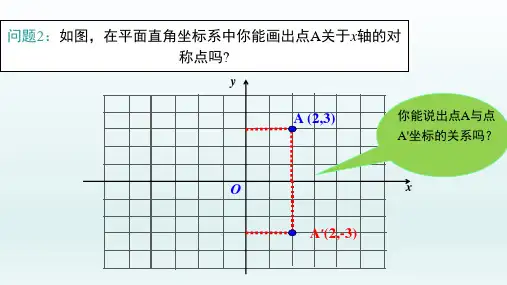
如图，你能在平面直角坐 标系中画出点A关于y轴的 对称点吗?
·A (2,3)
-4 -3 -2 -1 O 1 2 3 4 5 x -1
演讲人：XXXXXX 时 间：XX年XX月XX日
系中,你能画出点A关于 4
x轴的对称点吗?
3
2
1
-4 -3 -2 -1 O -1 -2 -3
-4
·A (2,3)
x
12345
你能说出点A 与点A′坐标 的关系吗？
y
5 4 3 2 1
-4 -3 -2 -1 O -1 -2 -3 -4
点A与点A′横坐标相同， 纵坐标互为相反数.
·A (2,3)
x
1 23 4 5
-2
对称的图形，
-3
-4
即△A′B′C′.
技巧:对于这类问题,只要先求出已知图形中的一些特殊 点(如多边形的顶点)的对应点的坐标,描出并连接这些点, 就可以得到这个图形的轴对称图形.
【跟踪训练】
1.点P(-5, 6)与点Q关于x轴对称，则点Q的坐标为 _(-__5__,-_6__)__. 2.点M(a, -5)与点N(-2, b)关于x轴对称，则 a=___-2__,b =___5__.
3.点P(-3, 2)与点Q关于y轴对称，则点Q的坐标为 _(_3__,_2__)___.
4.点M(a, -6)与点N(-2, b)关于y轴对称，则a=__2___, b =__-_6__.
1.完成下表:
已知点
(3,-3) (-1,2) (-8,-5) (0,-1) (4,0)
关于x轴的对称点 关于y轴的对称点
通过本课时的学习，需要我们掌握：
1.关于x轴对称的点横坐标相等，纵坐标互为相反数. 关于y轴对称的点横坐标互为相反数，纵坐标相等.
2.在平面直角坐标系中画一个图形关于x轴或y轴的对 称图形：先求出已知图形中的一些特殊点(如多边形的顶 点)的对应点的坐标,描出并连接这些点,就可以得到这个 图形的轴对称图形.
13.2 画轴对称图形 第2课时
1.探索利用坐标来表示轴对称. 2.掌握关于x轴、y轴对称的点的坐标特点.
如
已知点A和一条直线MN，你能画出这个点关于已知直线 的对称点吗?
过点A作AO⊥MN于O, 然后延长AO至OA′,使AO=OA′.
M
A
O
A′
N ∴ A′就是点A关于直线MN的对称点.
y
如图，在平面直角坐标 5
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
21
结束语
当你尽了自己的最大努力时，失败也是伟大的 ，所以不要放弃，坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End
(3, 3) (-3,-3)
(-1,-2) (-8,5) (1, 2) (8,-5)
(0,1) （4，0） (0, -1) (-4,0)
2.已知点P(2a+b,-3a)与点P′(8,b+2). 若点P与点P′关于x轴对称，则a=__2___,b=___4____. 若点P与点P′关于y轴对称，则a=__6___,b=__-_2_0___.
3.如图,分别
y
作出点P,M,N 关于直线x=1 的对称点, 你能发现它 们坐标之间 分别有什么 -4
5
P(-2,3) 4 ·3 2 M(-1,1) ·1
-3
-2
-1
0 -1
关系吗?
·
-2
N(-3,-2)
-3
-4
x=1
P′(4,3) ·
M′ (3,1) ·
12345x ·
N′ (5,-2)
（1）在平面直角坐标系中,点(x,y)关于直线x=1对称点
·A′(2,-3)
在平面直角坐标系中画出下列各点
关于x轴的对称点. y
5 4
· B (-4, 2) 3 2
1
-4 -3 -2 -1-O1 -2 -3
-4
1 2 3 4 5x
· C(3, -4)
关于x轴 对称的点 的坐标具 有怎样的 关系？
y
5 4
· B (-4, 2) 3 2 1
·-4 -3 -2 -1-O1 -2