当前位置：文档之家 › 第二章 原子光谱项

第二章 原子光谱项

  • 格式：ppt
  • 大小：131.50 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

原子光谱与原子光谱项

原子光谱与原子光谱项
3 1 36
状态数
7 5 3, 5
C6
2
65 2
15 只能有 15 个状态
不能只由量子数写光谱项, 必须考虑空间可能的状态, 必须合理, 即必须挑出满足 Pauli (由角动量直接耦合的状态中) 原理的空间状态
16
17
18
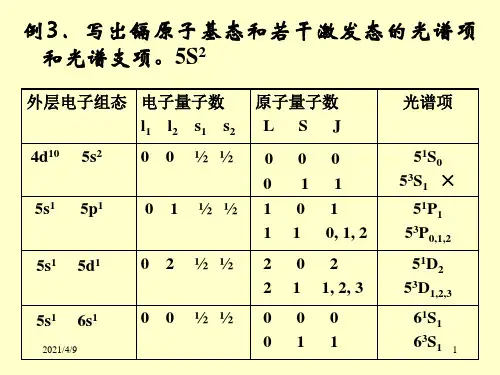
写光谱项:
M
L
2
M
S
0
L 2
1
D
组态
→ ①各电子量子数
②
LSJ
③ 状态数
① H 原子,
1 基态电子组态( 1 S )
S 电子
l 0
s
1 2
L 0
,
S
1 2
2
,
J
1 2
S,
2
S1
2
状态数 ( 2 0 1)( 2
1 2
1) 2
14
② He 原子
l1 0
( 1S )
2
, l2 0 ,

只考虑开壳层的光谱项
15
③
2 2 2 C 原子 (1 S ) ( 2 S ) ( 2 P )
l1 1 , l 2 1 ,
S1
3
L 2 .1 .0
1 2
,
S2
1 2
3
,
S 1 .0
3
D 3 , 2 ,1
1
P2 ,1 , 0
1
S1
1
D2
P1
5 3 1, 3
S0
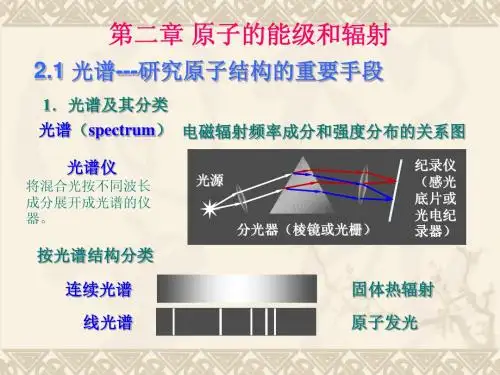
原子角动量 原子多重态 (多重性)
2S 1,
电子组态相同 , 空间状态不同 , 因而原子量子数不同 , 能量也不同。

第2章 原子结构 原子光谱项 3

第2章 原子结构 原子光谱项 3
●原子的微观能态：原子在磁场作用下的运动状态。原子的
微观能态又与原子的磁量子数mL，mS和mJ有关。
2、原子的光谱项的推求
1) 等价电子组态
等价(equivalence)电子：具有完全相同的主量子数(quantum number)和角量子数的电子 。
由于受Pauli原理和电子不可分辨性的限制，等价电子组态的光谱 项的求法与非等价电子的不同。
一种推求基谱项的简便方法
(1) 在不违反Pauli原理前提下，将电子填入轨道， 首先使每个电子ms尽可能大，其次使m也尽可能大；
(2) 求出所有电子的ms之和作为S，m之和作为L； (3) 对少于半充满者，取J=L-S；对多于半充满者， 取J=L+S.
d2
2 1 0 -1 -2
mS1, S1
L-S =2
电子轨道运动间的相互作用； 电子自旋运动间的相互作用； 轨道运动与自旋运动间的相互作用；
1. 角动量的耦合方案
j-j 耦合 l1 j, s1j→j1 ； l2 , s2 →j2
j1 ， j2→J
适合于重原L子（SZ＞40）
※ L-S耦合 l1,l2→L ；s1,s2 →S
L，S →J
适合于轻原子（LZ≤S40）
五、基谱支项
能量最低的光谱支项称为基谱支项。
可根据保里原理和洪特规则直接求得。先找出Ms 最大情况下ML
最大的状态，然后确定其S,L,J值，以这些值构成2S+1LJ，即为最稳
定的基谱项。
例：求氧原子基态的基谱项。
O:1s22s22p4，p轨道中4个电子的ms 最大时ML 最大的一种排布为：
↑↓ m: 1
例：2.电子组态为3p13d1的光谱项。
l 1 1 ,l 2 2 ,L 3 ,2 ,1 ,s 1 s 2 1 2 ,S 1 ,0 ,光 谱 项 为 3 F , 1 F , 3 D , 1 D , 3 P ,1 P

第二章_原子光谱项

第二章_原子光谱项
按照上述原则，电子依次排布到各个n，l确定的轨道上， 以此表示的电子排布方式称为电子组态。例：1s22s22p6
2.2 多电子原子的量子数
电子组态——原子中n，l 为一定值的电子排布方式
原子微观状态——原子中所有电子的轨道和自旋状态的总 和。
闭壳层组态——一个原子微观状态(各个电子的m，ms均确定) 开壳层组态——一组原子微观状态(各个电子的m，ms不确定)
在无外磁场时，这些状态均属同一能级。在有外磁场 存在时，由于原子磁距与外磁场相互作用，这（2J+1） 个微态将被劈裂开来，这就是塞曼效应
2.3 原子光谱项计算
例1：计算s1组态所对应的光谱项 解：s1组态的l=0，只有一个电子，s=1/2 所以：L=0，S=1/2 所以：s1组态所对应的光谱项为：2S J=L+S=1/2 所以，光谱支项为来子规原 定子 ，的 光运谱动学状上态常可将用不同L，的S状，态J，按mLJ，4个S，量J子数 值记成符号2S+1L，称为光谱项。右上角2S+1称为 光谱多重性，S=0，2S+1=1，称为单重态，S=1， 2S+1=3称为三重态。
原子光谱项反映了原子中电子间复杂的相互作用， 它与原子的电子组态共同决定原子的能量
解 4f3组态的l=3，N=3，故S=3/2，1/2
① S=3/2组：Nα=3，Nβ=0 MαL,max=3+2+1=6；Lα=6，4，2，0，3 MβL,max=Lβ=0 所以：L=6，4，3，2，0，光谱项为4I，4G，
4F，4D，4S
② S=1/2组： Nα=2，Nβ=1 MαL,max=3+2=5；Lα5，3，1 MβL,max=Lβ=3
L取值
01
表示符号 S P

原子光谱项

原子光谱项

L 2S 1 J
2S+1为光谱的多重度 J为轨道-自旋相互作用的光谱支项
原子光谱项记作2S+1L, 光谱支项记作2S+1LJ ,
L = 0 1 2 3 4 5 6 ……
符号 S P D F G H I ……
谱项能级高低的判断：洪特规则的另一种表达
（1）原子在同一电子组态时，S 大者能量低。 （2）S 相同时，L大者能量低。 （3）一般，L 和 S相同时，电子少于或等于半充满时 J
——原子的电子组态(Electron Configuration)：多电子原子 不仅要考虑电子各自的轨道运动，还要考虑各电子的自旋 运动。对于无磁场作用下的原子状态，由量子数n、l表示 无磁场作用下的原子状态，称为组态。能量最低的称为基 态，其它称为激发态。 ——原子的微观状态(Microscpic State)：在磁场作用下的 原子状态，需考虑量子数m、ms，称为原子的微观状态。 ——原子能态(Energy State)：当考虑到电子之间的相互作 用时，电子组态就不是能量算符的本征态，每个电子的四 个量子数就不能很好地表征电子的运动状态。能反映原子 整个状态，并与原子光谱直接相联系的是原子能态。
1P1 =(L=1,S=0: mL=-1/0/1; mS=0（含在1D2中）
(2)等价电子的光谱项
等价组态光谱项不能采用非等价组态光谱项的推求方 法，因为受pauli原理的限制，微观状态数大大减少，光谱 项推求的难度增大。例如n p 1 m p 1组态的微观状态数有
C6 1C6 156 !!1!56 !!1!36种
小，能量低；电子多于半充满时，J大，能量低。
多电子原子的能态——光谱项的推求
• L-S偶合：适用于电子之间的轨道角动量和自旋角动量相 互作用强于每个电子自身轨道角动量与自旋角动量相互作

原子发射光谱法

原子发射光谱法
在原子谱线表中，罗马数Ⅰ表示中性原子发射光谱的 谱线，Ⅱ表示一次电离离子发射的谱线，Ⅲ表示二次电 离离子发射的谱线例如Mg Ⅰ285.21nm为原子线，MgⅡ
3
第一节 基本原理
280.27nm为一次电离离子线。
二、原子能级与能级图
原子光谱是原子的外层电子（或称价电子）在两个 能级之间跃迁而产生。原子的能级通常用光谱项符号表 示：
S 为总自旋量子数，自旋与自旋之间的作用也较强 的，多个价电子总自旋量子数是单个价电子自旋量子数ms 的矢量和。
S = ms,i 其值可取0，±1/2，±1，±3/2，
J 为内量子数，是由于轨道运动与自旋运动的相互
7
第一节 基本原理
作用即轨道磁矩与自旋量子数的相互影响而得出的，它 是原子中各个价电子组合得到的总角量子数L与总自旋量 子数S的矢量和。
n2s+1LJ
核外电子在原子中存在运动状态，可以用四个量子 数n、l、m、ms来规定。
主量子数n决定电子的能量和电子离核的远近。
4
第一节 基本原理
角量子数l 决定电子角动量的大小及电子轨道的形状， 在多电子原子中也影响电子的能量。
磁量子数m决定磁场中电子轨道小。
第二章 原子发射光谱法
原子发射光谱法是一种成分分析方法，可对约70种 元素（金属元素及磷、硅、砷、碳、硼等非金属元素） 进行分析。这种方法常用于定性、半定量和定量分析。
在一般情况下，用于1%以下含量的组份测定，检出 限可达ppm，精密度为±10%左右，线性范围约2个数 量级。但如采用电感耦合等离子体（ICP）作为光源，则 可使某些元素的检出限降低至10-3 ~ 10-4ppm，精密度达 到±1%以下，线性范围可延长至7个数量级。这种方法 可有效地用于测量高、中、低含量的元素。

原子物理学第二章氢原子光谱

原子物理学第二章氢原子光谱
n2
激发态（excited state） 电子轨道
巴耳末系 帕邢系
n 3
பைடு நூலகம்
赖曼系
2
能级（energy level）
1
n
1
2
3
4
En R Tn 2 n hc
hcR En 2 n
根据波尔理论，氢原子的光谱可以作如下的解释: 氢原子在正常状态时，它的能级最小，电子 位于最小的轨道，当原子吸收或放出一定的 能量时，电子就会在不同的能级间跃迁，多 余的能量便以光子的形式向外辐射，从而形 成氢原子光谱。
e Ze
Ze2 F 4π 0 r 2
e2 Ze2
2
n2 Z c rn a1 vn n 1, 2, 3, Z n Z 2 hcR 1 Z 2e2 En 2 2n 4π 0 a1 n2

En2 En1 hc
1 1 1 1 Z R 2 2 R 2 2 n1 Z n2 Z n1 n2
2 2 e 4 RA 2 3 (4 0 ) h c
2 2 me 4 M M R 2 3 (4 0 ) h c M m M m
（3）
我们看到，当原子核质量M→∞时， RA=R∞=109737.31cm-1。在一般情况下，可以 通过（3）式来计算里德伯常数。
里德伯常数随原子核质量变化的情况曾被 用来证实氢的同位素—氘的存在。还可以测 定原子量、电子的核质比、质子的质量和电 子的质量之比等。 起初有人从原子质量的测定问题估计有质量 是2个单位的中氢。 1932年，尤雷在实验中发现，所摄液氢赖 曼系的头四条谱线都是双线，双线之间波长 差的测量值与通过里德伯常数 R 计算出的双 线波长差非常相近，从而确定了氘的存在。

高中物理第二章原子结构2.3光谱氢原子光谱教科35


审题,然后(ránhòu)利用巴尔末公式1
计算。
RH(212
1 n2
)
进行有关的
第四十四页，共五十五页。
【拓展例题】考查内容(nèiróng):氢原子光谱的问题计算 氢原子光谱在可见光的范围内有两条谱线,其波长分别为 654.55×10-9m和484.85×10-9m,根据巴尔末公式,求所对应的n. 【思路点拨】根据给出的光谱线对应的波长应用巴尔末公 式确定出n。
第二十四页，共五十五页。
【补偿训练】 (多选)下列关于光谱的说法正确的是 ( ) A.连续光谱就是由连续发光的物体产生的光谱,线状谱是线状光 源产生的光谱 B.通过对连续谱的光谱分析(ɡuānɡ pǔ fēn xī),可鉴定物质成分 C.连续光谱包括一切波长的光,线状谱只包括某些特定波长的 光
第二十五页，共五十五页。
第四十二页，共五十五页。
【解析】选A、C。巴尔末公式是分析(fēnxī)氢原子的谱线得到的 一个公式,它只反映氢原子谱线的一个线系,故A对,D错,公式 中的n只能取不小于3的正整数,B错,C对。
第四十三页，共五十五页。
【温馨提示】
对氢原子光谱的理解及其应用是高考的热点,特别是氢
原子光谱的计算问题,在解决本类问题时,一定要仔细
第四页，共五十五页。
二、氢原子光谱 1.许多情况(qíngkuàng)下光是由原子内部电子的运动产生的,因此 光谱研究是探索原子结构的一条重要途径。 2.巴尔末公式: =_1____R__H_(_21_2 (n=n132,)4,5,…)其中RH叫 作里_德__堡__常__数__(_c_há。ngs其hù)值为RH=1.097 373 156 854 8×
第九页，共五十五页。
1.光谱的分类:

第二章-原子光谱--2

2. 按光谱项画出能级图
3. 根据光谱跃迁选择定则画出可能的跃迁。
电子组态
电子量子数 l1 l2 s1 s2
原子量子数 光谱项 LS J
1s 1s
0 0 1/2 1/2 0 0 0 11S0 0 1? 1 13S1 ×
1s 2s
0 0 1/2 1/2 0 0 01
0 21S0 1 23S1
1s 2p
2021/4/9
5
任何原子的状态，基态或激发态，可以看作它的一次电 离离子加上一个电子形成的。而它的一次电离离子的状 态又同周期表顺序前一个元素相似，所以 ，由前一个元 素的状态可以推断后继元素的状态。这可以按照对2电 子体系推求状态的法则进行。把原有原子或离子的总轨 道角动量量子数（用Lp表示）代替2电子体系中的一个
2021/4/9
e
8
原子光谱学中，这种以动能转变为激发能的碰撞过程 称为第一类非弹性碰撞。原子发射光谱发现采用的火焰、 电弧和火花光源中，这种碰撞激发总是占优势。
受激原子与激发态粒子相互碰撞亦可能被激发或电离， 这类碰撞称为第二类非弹性碰撞。在一般情况下，由于激 发态粒子数很小，这类非弹性碰撞通常可以忽略。但是， 当等离子体中有较大密度的激发态原子、离子和分子时 （高温下），第二类非弹性碰撞引起的激发作用显著增强， 甚至起重要作用。如空心阴极放电、辉光放电，亚稳态载 气原子存在 (亚稳态指寿命特别长的稳定激发态)。
A + hv →A* (ΔE=hv)
7
2.4 原子的激发和光谱发射（谱线的产生）
2.4.1 原子受激方式
在无外界作用时，原子中的各电子都尽可能地处于能 量最低的基态。若基态原子受到外界能量的扰动而引起内 能变化，使外层电子跃迁到能量较高的激发态，则该原子 称为受激原子。若原子获得的能量等于或大于原子的电离 能，原子失去价电子成为离子。原子的激发和电离主要有

原子物理第二章氢原子光谱

电子轨道和能量分立
1 Ze 2 En 2 4π 0 rn
n 1, 2, 3,
(2) 跃迁（transition）假设
h
h
原子在不同定态之间跃迁，以电磁 辐射形式吸收或发射能量。
hv En Em
吸收 发射
频率条件
跃迁频率：
En Em h
(3) 角动量量子化假设 为保证定态假设中能量取不连续值，必须 rn 取不连续值， 如何做到？
H H H
1 1 22 n 2 n 3, 4, 5,
氢原子的Rydberg常数
RH 1.0967758 107 m1
巴尔末线系限：
RH v 2 2
2.H原子光谱的其它线系
（远紫外）赖曼系：
1 1 v RH 2 2 n 2,3, 4 1 n
线系的一般表示： 令：
1 1 v RH 2 2 n m RH RH T ( m) 2 T ( n) 2 m n
光谱项
并合原则： v T (m) T (n)
每一谱线的波数差都可表达为二光谱项之差
这些经验公式是否反映了原子内部结构的规律性？？
2.3 玻尔氢原子理论

Ze 2 r 40 mv 2 1
4 0 n 2 h 2 解得 r ; n 2 2 4 mZe
h p mvr n 2
nh Vn 2 mr
我们引入
4 0 h2 a1 2 2 0.529166 1010 m 4 me
则量子化的轨道半径为
n2 rn a1 Z
非量子化的状态与连续光谱 我们已经知道，所有的光谱线分为一系列线 系，每个线系的谱线都从最大波长到最小波 长（系线）；可是试验中观察到在系限之外 还有连续变化的谱线。这是怎么回事呢？

结构化学省队资料-STRUCT-原子光谱项-2012-2


L=3,2,1 S=1,0, 2S+1=3,1
谱项: 3F, 3D, 3P; 1F, 1D, 1P
支项: 以3F 为例， L=3 ， S=1 ，J=4，3，2
所以3F有三个支项: 3F4， 3F3， 3F2
第二章-原子光谱项
28
2. 等价组态光谱项
等价组态光谱项不能采用非等价组态光谱项那种 求法，否则将会出现一些违反Pauli原理的情况, 最基本的作法是 “行列式波函数法” .
例:由“行列式波函数法”推求等价组态p2的光谱
项. 微状态数:
C62
6! 2!(6
2)!
15
第二章-原子光谱项
30
(a). 画出所有不违反Pauli原 理的15个微状态:
(b). 按下列步骤计算、分类来
确定谱项:
第二章-原子光谱项
31
微状态
ml
1
0
-1
ML=ml MS= ms
1+1=2
2
0
辐射过程: 电子从激发态 回到基态, 辐射一定频率 的光.
时间: 10-8 s
第二章-原子光谱项
2
图: 原子光谱精细结构
第二章-原子光谱项
3
原子光谱项 (spectroscopic term)
1. 多电子原子体系的能级
➢由主量子数n、角量子数l描述的原子中电子排布方式 称为原子的电子“组态(configuration)”.
第二章-原子光谱项
23
原子光谱项和光谱支项的求法
➢在原子光谱项中L以光谱记号标记,取值对应大写 字母:
L = 0 1 2 3 4 5 ……
S P D F G H ……
注意两处S的不同含义: 光谱支项中若为S, 那是 L=0的标记; 光谱支项左上角的S则是总自旋角动 量量子数, 对于具体的谱项是一个具体值.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
即：在一组能量相同的轨道上，电子尽可能以自旋相同的方向分占 在一组能量相同的轨道上， 不同的轨道。 不同的轨道。 能量间并的轨道上全充满、半充满或全空的状态是比较稳定的。 能量间并的轨道上全充满、半充满或全空的状态是比较稳定的。
按照上述原则，电子依次排布到各个n 确定的轨道上， 按照上述原则，电子依次排布到各个n，l确定的轨道上， 以此表示的电子排布方式称为电子组态。 以此表示的电子排布方式称为电子组态。例：1s22s22p6
例1：氦原子的基态对应1个原子微观状态，而其第一激发 氦原子的基态对应1个原子微观状态， 对应有4个原子微观状态； 态(1s12s1)对应有4个原子微观状态； 碳原子的基态(1s 对应有15个原子微观状态 个原子微观状态。 例2：碳原子的基态(1s22s22p2)对应有15个原子微观状态。
每种电子组态还可能包含着不止一种的能量状态， 每种电子组态还可能包含着不止一种的能量状态，这些能量状态可用 原子的量子数S 来标记， 原子的量子数S，L，J，MJ来标记，用其写成一定的符号表示该原子 微观状态对应的能级——原子光谱项 微观状态对应的能级——原子光谱项
L取值 表示符号 L取值 表示符号 0 S 7 K 1 P 8 L 2 D 9 M 3 F 10 N 4 G 11 O 5 H 6 I
2.2 多电子原子的量子数
原子的自旋量子数S 原子的自旋量子数S 原子的自旋量子数也是采用Clebsch-gordan数列给 原子的自旋量子数也是采用Clebsch-gordan数列给 。（s 偶合） 出。（s-s偶合） 对于自旋量子数为s 的两个电子， 对于自旋量子数为s1和s2的两个电子，总的自旋量子 可由下列规则求出： 数S可由下列规则求出： S=|s1+s2|，|s1-s2| 由于s=1/2，所以S的值为1 由于s=1/2，所以S的值为1和0 当电子数为3 当电子数为3时，再用一次角动量偶合规则求得 S=3/2， S=3/2，S=1/2 电子数为偶数时， 或正整数， 电子数为偶数时，S取0或正整数，当电子数为奇数 时，S取半整数
2.1基态原子核外电子排布的规则 2.1基态原子核外电子排布的规则
基态的原子核外电子应遵从三条原则： 基态的原子核外电子应遵从三条原则：
泡利不相容原理：一个原子中不可能存在两个具有相同的4 泡利不相容原理：一个原子中不可能存在两个具有相同的4个量子 数的电子， 数的电子，
一个原子轨道最多只能排两个电子，而且自旋必须相反。 一个原子轨道最多只计算
辽宁大学刘国范教授的快速算法 给定一个n 组态， 给定一个nlN组态，则，l和N是已知的，由总电子数N可以求出此组态 是已知的，由总电子数N 的总自旋量子数S S=N/2，N/2- N/21/2， 的总自旋量子数S，即S=N/2，N/2-1，N/2-2，…，0或1/2，在确定 值中按自旋不同的状态确定不同自旋方向的电子数N 的S值中按自旋不同的状态确定不同自旋方向的电子数Nα，Nβ，然后 再由N 分别计算出M 具体计算公式为： 再由Nα，Nβ分别计算出MαL,MAX和MβL,MAX，具体计算公式为： MαL,MAX=∑（l+1-K），（K=1，2，…， Nα） =∑（ +1- ），（K=1， MαL,MAX和MβL,MAX确定了Lα，Lβ的最大值，然后，在依据一定的规则确 确定了L 的最大值，然后，在依据一定的规则 一定的规则确 的其它较小值。 定Lα，Lβ的其它较小值。 按矢量和定则求出总轨道角动量量子数L 最后，再由Lα，Lβ按矢量和定则求出总轨道角动量量子数L 最后，再由L
磁量子数m：描述着电子云在空间的伸展方向，取值受角量子数l 磁量子数m：描述着电子云在空间的伸展方向，取值受角量子数l的 限制，m=0， 限制，m=0，±1， ±2，…， ±l 自旋磁量子数ms：描述原子中的电子的自旋运动，取值为±1/2分别 自旋磁量子数ms：描述原子中的电子的自旋运动，取值为±1/2分别 表示同一原子轨道中电子的两种取向，即顺时针方向和逆时针方 向。
能量最低原理：为了使原子系统能量最低， 能量最低原理：为了使原子系统能量最低，在不违背泡利不相容 原理的前提下，电子尽可能地先占据能量最低的轨道。 原理的前提下，电子尽可能地先占据能量最低的轨道。
这个状态就是原子系统的基态。 这个状态就是原子系统的基态。
洪德原则：在等能量（n,l相同）的轨道上，自旋平行电子数越多 洪德原则：在等能量（n,l相同）的轨道上， 原子系统的能量则越低。 原子系统的能量则越低。
轨道角动量量子数l 轨道角动量量子数l，简称角量子数
决定电子的原子轨道角动量的大小，描述电子云的形状 当n值一定时，不同的l对电子的能量也稍有影响，l越大能量越高 值一定时，不同的l对电子的能量也稍有影响，l l取值为0，1，2，3， …，（n-1）等n个从0开始的正整数 取值为0 ，（n ）等n个从0
3. 最大的S值组中L取Lα和Lβ按矢量和定则组合 最大的S值组中L 得到的数值，其余每组的L 得到的数值，其余每组的L取Lα和Lβ组合 得到的数值减去前一组L 得到的数值减去前一组L余下的值 4. 当N<=2l+1（即电子数小于等于半充满） N<=2l+1（即电子数小于等于半充满） 时，nl2(2l+1)时，nl2(2l+1)-N组态可以看作是在全充满的 2(2l 组态中添加N nl2(2l+1)组态中添加N个正电子的系统。正 电子除电荷的符号外，与电子的性质完全 一样，因此，它们之间的作用与电子之间 的作用一样，所以， nlN组态产生的光谱 项与n 2(2l+1)项与nl2(2l+1)-N组态光谱项全同，只是光谱 支项后者是倒易的
计算原则
1.
依据S值由大到小分组求光谱项。每组根据S值确定N 依据S值由大到小分组求光谱项。每组根据S值确定Nα和Nβ数，再求出 MαL,MAX和MβL,MAX，最后确定Lα和Lβ值。 ,MAX，最后确定L
Nα = 0
2. 当
时或 Nβ = 2l +1 时， MαL,MAX=0，则Lα=0； =0， =0；
2.3 非等价电子原子光谱项计算
例2：计算s1p1组态所对应的光谱项 计算s =0， 解：l1=0，l2=1 所以：L=1，S=1， 所以：L=1，S=1，0 所以： 组态所对应的光谱项为： 所以：s1p1组态所对应的光谱项为：3P，1P 例3：计算2p13p1组态所对应的光谱项 计算2p 3p1组态所对应的光谱项 =1， 解：l1=1，l2=1 所以：L=2， S=1， 所以：L=2，1，0，S=1，0 所以： 组态所对应的光谱项为： 所以：p1p1组态所对应的光谱项为：3D，3P， 3S， 1D， 1P，1S
2.3 原子光谱项
多电子原子的运动状态可用L 多电子原子的运动状态可用L，S，J，mJ 4个量子 数来规定，光谱学上常将不同的状态按L 数来规定，光谱学上常将不同的状态按L，S，J数 称为光谱项。右上角2S+1称为 值记成符号2S+1L，称为光谱项。右上角2S+1称为 光谱多重性，S=0，2S+1=1，称为单重态，S=1， 光谱多重性，S=0，2S+1=1，称为单重态，S=1， 2S+1=3称为三重态 2S+1=3称为三重态。 称为三重态。 原子光谱项反映了原子中电子间复杂的相互作用， 原子光谱项反映了原子中电子间复杂的相互作用， 它与原子的电子组态共同决定原子的能量 光谱多重性与电子自旋引起的能级劈裂以及谱线 劈裂数目有关，因此， 劈裂数目有关，因此，不仅能够反映总自旋角动 量的大小， 量的大小，也表明该状态的自旋角动量在磁场方 向分量的可能数目。 向分量的可能数目。
2.3 原子光谱项计算
例1：计算s1组态所对应的光谱项 计算s 组态的l=0，只有一个电子， 解：s1组态的l=0，只有一个电子，s=1/2 所以：L=0， 所以：L=0，S=1/2 所以： 组态所对应的光谱项为： 所以：s1组态所对应的光谱项为：2S J=L+S=1/2 所以， 所以，光谱支项为2S1/2
2.2 多电子原子的量子数
电子组态——原子中 电子组态——原子中n，l 为一定值的电子排布方式 原子中n 原子微观状态——原子中所有电子的轨道和自旋状态的总 原子微观状态——原子中所有电子的轨道和自旋状态的总 和。
闭壳层组态——一个原子微观状态 各个电子的m ms均确定 闭壳层组态——一个原子微观状态(各个电子的m，ms均确定) 一个原子微观状态( 均确定) 开壳层组态——一组原子微观状态 各个电子的m ms不确定 一组原子微观状态( 不确定) 开壳层组态——一组原子微观状态(各个电子的m，ms不确定)
2.2 多电子原子的量子数
原子的轨道角动量量子数L 原子的轨道角动量量子数L
等于每个电子的轨道角量子数的矢量和 L=∑ 即：L=∑li 若一个电子的角量子数为l 另一个电子的角动量为l 若一个电子的角量子数为l1，另一个电子的角动量为l2，其矢量 和为： 和为： L=（l1+l2),(l1+l2-1),…,|l1-l2| L=（ ),(l 1),…,|l 采用单电子系统一样的符号来表示L的各种取值状态， 采用单电子系统一样的符号来表示L的各种取值状态，但是用大 写字母表示。 写字母表示。
2.2 多电子原子的量子数
原子的总角动量量子数J 原子的总角动量量子数J
有两种办法求算总角动量量子数J 有两种办法求算总角动量量子数J
L-S偶合：把每个电子的s合并成S（S=∑si），l合并 偶合：把每个电子的s合并成S S=∑s ），l L=∑l ），然后再将 然后再将L 合并成J J=L+S） 成L（L=∑li），然后再将L和S合并成J（J=L+S） j-j偶合：把s和l先合并成j，然后再将j合并成J 偶合： 先合并成j 然后再将j合并成J
当 Nα =1 时或Nβ=2l时， MαL,MAX= ，则Lα= l 时或N =2l时 ； l 当
1< Nα < 2l