旋转作图题训练题

23.1 图形的旋转旋转的概念将一个图形绕一个定点转动一定的角度，这样的图形运动称为图形的旋转.定点称为旋转中心，旋转的角度称为旋转角.注意：旋转的三要素：旋转中心、旋转方向和旋转角度；图形的旋转不改变图形的形状、大小.题型1：旋转中的概念及对应元素1.下列运动中，属于旋转运动的是（ ）A．小明向北走了4 米B．一物体从高空坠下C．电梯从1 楼到12 楼D．小明在荡秋千【答案】D【解析】【解答】解：A. 小明向北走了 4 米，是平移，不属于旋转运动，A不合题意；B. 一物体从高空坠下，是平移，不属于旋转运动，B不合题意；C. 电梯从1 楼到12 楼，是平移，不属于旋转运动，C不合题意；D. 小明在荡秋千，是旋转运动，D符合题意．故答案为：D．【分析】根据图形旋转的定义求解即可。

【变式1-1】如图，线段AB绕着点O旋转一定的角度得线段A'B'，下列结论错误的是（ ）A．AB＝A'B'B．∠AOA'＝∠BOB'C．OB＝OB'D．∠AOB'＝100°【答案】D【解析】【解答】∵线段AB绕着点O旋转一定的角度得线段A'B'，∴AB＝A′B′，∠AOA′＝BOB′，OB＝OB′，故A，B，C选项正确，∵∠AOB和∠BOB′的度数不确定，∴∠AOB′≠100°，故D选项错误.故答案为：D.【分析】由旋转的性质可得AB＝A′B′，∠AOA′＝BOB′，OB＝OB′，据此判断.【变式1-2】如图（1）中，△和△都是等腰直角三角形，∠和∠都是直角，点在上，△绕着点经过逆时针旋转后能够与△重合，再将图（1）作为“基本图形”绕着点经过逆时针旋转得到图（2）.两次旋转的角度分别为（ ）A．45°，90°B．90°，45°C．60°，30°D．30°，60°【答案】A【解析】根据图1可知，∵△ABC和△ADE是等腰直角三角形，∴∠CAB=45°，即△ABC绕点A逆时针旋转45°可到△ADE；如右图，∵△ABC和△ADE是等腰直角三角形，∴∠DAE=∠CAB=45°，∴∠FAB=∠DAE+∠CAB=90°，即图1可以逆时针连续旋转90°得到图2．故选A．旋转的性质一个图形和它经过旋转所得到的图形中：(1)对应点到旋转中心的距离相等； (2)两组对应点分别与旋转中心连线所成的角相等.　注意：图形绕某一点旋转，既可以按顺时针旋转也可以按逆时针旋转.题型2：旋转的性质及旋转中心的确定2.如图，△DEF是由△ABC绕着某点旋转得到的，则这点的坐标是( )A．(1，1)B．(0，1)C．(-1，1)D．(2，0)【答案】B【解析】【解答】解：如图，连接AD、BE，作线段AD、BE的垂直平分线，两线的交点即为旋转中心O′.其坐标是(0，1).故答案为：B.【分析】连接AD、BE，作线段AD、BE的垂直平分线，根据旋转的性质即可求解。

小升初数学专项练习一线名师严选内容，逐一攻克☆基本概念、基本原理、基础技能一网打尽☆点拨策略思路，侧重策略指导，拓宽眼界思路☆4.作旋转一定角度后的图形【小升初考点归纳】1．旋转作图步骤：（1）明确题目要求：弄清旋转中心、旋转方向和旋转角；（2）分析所作图形：找出构成图形的关键点；（3）找出关键点的对应点：按一定的方向和角度分别作出各关键点的对应点；（4）作出新图形：顺次连接作出的各点．（5）写出结论：说明作出的图形．2．中心对称作图步骤：（1）连接原图形上的所有特殊点和对称中心；（2）再将以上连线延长找对称点，使得特殊点与对称中心的距离和对称点与对称中心的距离相等；（3）将对称点按原图形的形状顺次连接起来，即可得出关于对称中心对称的图形．【经典例题】一．选择正确的答案，把序号填在括弧中（共1小题）1．（2016•长沙模拟）下面图形中，以某一边为轴旋转一周，可以得到圆锥的是（）A．B．C．D．【解析】解：直角三角形沿一条直角边旋转一周得到的几何体是一个圆锥．故选：A．二．操作题（共14小题）2．（2019春•南京月考）（1）将先向下平移5格，再向右平移13格．（2）将平行四边形沿A点顺时针方向旋转90°．【解析】解：（1）将先向下平移5格（下图红色部分），再向右平移13格（下图绿色部分）：（2）将平行四边形沿A点顺时针方向旋转90°（下图蓝色部分）：3．（2019春•枣阳市校级月考）（1）将图形A绕点O点顺时针旋转90°得到的图形B．（2）将图形B向右平移4格得到图形C．【解析】解：（1）将图形A绕点O点顺时针旋转90°得到的图形B（下图）：（2）将图形B向右平移4格得到图形C（下图）：4．（2018•泉州）（1）按要求画图．①将图中的三角形①绕O点顺时针旋转90°，画出旋转后的图形②．②将图中的三角形①平移，使平移后的三角形顶点O的位置在（9，5），画出平移后的图形③．【解析】解：根据分析可得，5．（2018春•新罗区期末）画一画：（1）把图形绕点O逆时针旋转90°．（2）把旋转后的图形向下平移两格．【解析】解：6．（2018•漳平市校级模拟）做一做，画一画（1）画出图形A的另一半，使它成为一个以直线a为对称轴的对称图形．（2）画出把图形B向右平移6格后得到的图形．（3）画出把图形C绕O点顺时针旋转90°后得到的图形．（4）用数对表示O点的位置是（8，6）．【解析】解：（1）画出图形A的另一半，使它成为一个以直线a为对称轴的对称图形．（2）画出把图形B向右平移6格后得到的图形．（3）画出把图形C绕O点顺时针旋转90°后得到的图形．（4）用数对表示O点的位置是（8，6）．故答案为：8，6．7．（2018春•隆化县校级期末）画出三角形AOB绕O点逆时针旋转180o后的图形．【解析】解：画出三角形AOB绕O点逆时针旋转180°后的图形（图中红色部分）：8．（2018春•卢龙县期中）画出三角形AOB绕点O逆时针旋转90度的图形．【解析】解：画出三角形AOB绕点O逆时针旋转90度的图形（图中红色部分）：9．（2018秋•廉江市期中）画出三角形AOB绕B点顺时针旋转90度后的图形．【解析】解：作图如下：10．（2018•兴仁县）按要求画一画．（1）画出图形A向右平移5格后得到的图形B．（2）画出图形B绕点O逆时针旋转90°后得到的图形C．【解析】解：（1）画出图形A向右平移5格后得到的图形B（下图）：（2）画出图形B绕点O逆时针旋转90°后得到的图形C（下图）：11．（2017春•海南区期末）画出三角形AOB绕O点顺时针旋转90度后的图形．【解析】解：根据题干分析画图如下：12．（2016春•洛阳月考）将长方形绕A点顺时针旋转90°．【解析】解：将长方形绕A点顺时针旋转90°（图中红色部分）：13．（2016春•新郑市校级月考）画出下面的图象中的三角形沿着A点顺时针旋转90度后的图形．【解析】解：三角形沿着A点顺时针旋转90度后的图形（红色部分）：14．（2016秋•永州期中）把如图的小三角旗绕点A沿顺时针方向旋转90度．再向右平移4格．分别画出旋转和平移后的图形．【解析】解：画图如下：15．（2016春•南海区期末）画出面积是3平方厘米的三角形AOB并绕O点逆时针旋转180o 后的图形．【解析】解：根据题干分析可得：三．解析题（共7小题）16．（2019春•东海县月考）按要求画一画．①将长方形绕A点逆时针旋转90°．②将小旗围绕B点逆时针旋转90°．【解析】解：作图如下：17．（2019春•古浪县校级期末）先将△ABC绕点C点顺时针旋转90°得到△A′B′C，再将△A′B′C′向下平移4格．【解析】解：先将△ABC绕点C点顺时针旋转90°得到△A′B′C，再将△A′B′C′向下平移4格．18．（2018春•抚宁区期末）画出绕点“O”顺时针旋转90度后的图形．【解析】解：作图如下：19．（2017秋•保定期末）画出三角形逆时针旋转90度后的图形．【解析】解：作图如下：20．（2018春•桃城区校级期末）（1）小鱼图从右下方移至左上方，先向上平移3格，又向左平移5格．（2）把梯形绕A点顺时针方向旋转90°，画出旋转后的图形．【解析】解：（1）根据题干分析可得：小鱼图从右下方移至左上方，先向上平移3格，再向左平移5格；（2）根据分析画图如下：故答案为：上、3、左、5．21．（2017春•绍兴期末）画出三角形AOB绕O点顺时针旋转90°后的图形．【解析】解：画出三角形AOB绕O点顺时针旋转90°后的图形：22．（2017春•绍兴期末）画出三角形AOB绕O点顺时针旋转90°后的图形．【解析】解：画出三角形AOB绕O点顺时针旋转90°后的图形：。

第2课时旋转作图1 •如图23-1-19 , E, F分别是正方形ABC啲边AB BC上的点，且BE= CF,连接CEDF将厶DCF绕着正方形的中心0按顺时针方向旋转到△ CBE的位置，则旋转角为() 某点旋转一个角度可以得到另一条线段，你认为这个旋转中心的坐标是3. 如图23-1-21，在平面直角坐标系中，△ ABC三个顶点的坐标分别为A(2,3)，巳1,1),Q5,1).(1) △ ABC平移后，其中点A移到点A(4,5)，画出平移后得到的△ ABC;(2) 把厶ABG绕点A按逆时针方向旋转90°,画出旋转后的△ ARG.A. 30°C. 60°2.如图23-1-20, A点的坐标为(一1,5)B. 45°D. 90°,B点的坐标为(3,3) , C点的坐标为(5,3) , D点的坐标为(3 , —1) •小明发现线段AB与线段CD存在一种特殊关系, 即其中一条线段绕着图23-1-19图23-1-204. 在4X4的方格纸中，△ ABO的三个顶点都在格点上.⑴在图23-1-22中画出与厶ABC成轴对称且与△ ABC有公共边的格点三角形(画出一个即可)；(2)将图23-1-23中的△ ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.AB R[¥| 2：^-I 22 图鬲I 站Cfil •拓牌创新5. 如图23-1-24所示，在平面直角坐标系中，有Rt△ ABC且A—1, 3),耳一3,—1), q —3, 3)，已知△ AAC是由△ ABC旋转变换得到的.(1) 旋转中心的坐标是_____，旋转角是_____;(2) 以⑴中的旋转中心为中心，分别画出△AAC顺时针旋转90°, 180°后的三角形；(3) 设Rt△ ABC的两直角边BGa, AG b,斜边AB= c,禾用变换前后所形成的图案证明勾股定理.参考答案【分层作业】1. D2. (1,1)或(4,4)3.略4 略5. (1)(0 ,0) 90°⑵略(3)略。

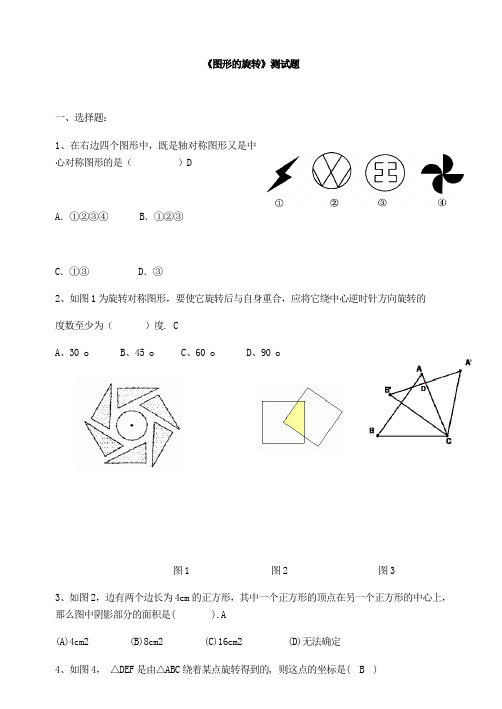
《图形的旋转》测试题一、选择题：1、在右边四个图形中，既是轴对称图形又是中心对称图形的是（）DA．①②③④ B．①②③C．①③ D．③2、如图1为旋转对称图形，要使它旋转后与自身重合，应将它绕中心逆时针方向旋转的度数至少为（）度. CA、30 oB、45 oC、60 oD、90 o图1 图2 图33、如图2，边有两个边长为4cm的正方形，其中一个正方形的顶点在另一个正方形的中心上，那么图中阴影部分的面积是( ).A(A)4cm2 (B)8cm2 (C)16cm2 (D)无法确定4、如图4，△DEF是由△ABC绕着某点旋转得到的, 则这点的坐标是( B )图5 图4 A. (1,1) B. (0,1) C. (−1,1) D. (2,0)二、填空题5、点a 4（，）与3b （，）关于原点对称，则a b += .-76、如图3，把三角形△ABC 绕着点C 顺时针旋转350，得到△A ＇B ＇C ，A ＇B ＇交AC 于点D ，若∠A ＇DC=900，则∠A 的度数是__________。

5507、如图5， △ABC 中, (ACB = 90(, (B = 30(, BC = 6, 三角板绕C 逆时针旋转, 当点A的对应点A' 落在AB 边上时即停止转动, 则BM 的长为 3 .8、如图6，△ABC 中, 已知∠C=90°, ∠B=50°, 点D 在边BC 上, BD=2CD. 把△ABC 绕着点D逆时针旋转m （0(<m<180(）度后, 如果点B 恰好落在初始Rt △ABC 的边上, 那么m = _______.80(或120(.三、解答题9、作图题（1）如图7，画出△ABC 绕点O 顺时针旋转60°所得到的图形．图6 BA CO图7 图8（2）如图8,在直角坐标系中,点P 的坐标为(3,4),将OP 绕原点O 逆时针旋转90°得到线段OP ′,(1)在图中画出线段OP ′;(2)P ′的坐标为 ______. (-4,3)1、如图，在△ABC 中，∠B=900，∠C=300，AB=1，将△ABC 绕顶点A 旋转1800，点C 落在C1处，则C C1的长为（ ）A ．24B ．4C ．32D ．522、如图，△ABC 中，∠ACB=1200，将它绕着点C 旋转300 后得到△DCE ，则∠ACE=∠A+∠E=3、如图，在Rt △ABC 中，∠ACB=90°，∠A=35°，以直角顶点C•为旋转中心，将△ABC 旋转到△A ′B ′C 的位置，其中A ′、B ′分别是A 、B 的对应点，且点B 在斜边A ′B ′上，直角边CA ′交AB 于D ，求∠BDC 的度数．4，如图，正方形ABCD 中，E 在BC 上，F 在AB 上且∠FDE=45°，•△DEC 按顺时针方向转动一个角度后成为△DGA ．（1）图中哪一个点是旋转中心？（2）旋转了多少度？（3）指出图中的对应点，对应线段和对应角；（4）求∠GDF 的度数．5、已知如图，正方形ABCD 中，E 为CD 边上一点，F 为BC 边上一点，CE=CF:(1)EBC FDC ∠∠与相等吗？（2）△DCF 能与△BCE 重合吗？（3）试判断BE 与DF 的位置关系并说明理由,6．如图所示，四边形ABCD 中，∠BAD=∠C=90°，AB=AD ，AE ⊥BC 于E ，△BEA 旋转后能与△DFA 重合．（1）旋转中心是哪一点？（2）旋转了多少度？（3）若AE=5cm ，求四边形ABCD 的面积．7，如图，K是正方形ABCD内一点，以AK为一边作正方形AKLM，使L，M，D在AK的同旁，连结BK和DM，试用旋转的思想说明线段BK与DM的关系．,8，.如图所示，等边△ABC中，D是AB边上的动点(不与A、B重合)，以CD为一边，向上作等边△EDC。

一、解答题（共30小题）1、如图，在边长为1的小正方形组成的网格中，△AOB的三个顶点均在格点上，点A、B的坐标分别为A（﹣2，3）、B（﹣3，1）．（1）画出坐标轴，画出△AOB绕点O顺时针旋转90°后的△A1OB1；（2）点A1的坐标为_________；（3）四边形AOA1B1的面积为_________．1题图 2题图2、△ABC在平面直角坐标系中的位置如下图，其中每个小正方形的边长为1个单位长度．（1）将△ABC向右移平2个单位长度，作出平移后的△A1B1C1，并写出△A1B1C1各顶点的坐标；（2）若将△ABC绕点（﹣1，0）顺时针旋转180°后得到△A2B2C2，并写出△A2B2C2各顶点的坐标；（3）观察△A1B1C1和△A2B2C2，它们是否关于某点成中心对称？若是，请写出对称中心的坐标；若不是，说明理由．5、（2010•鸡西）△ABC在如下图的平面直角坐标系中．（1）画出△ABC关于原点对称的△A1B 1 C1（2）画出△A1B1C1关于Y轴对称的△A2B2C2（3）请直接写出△AB2A1的形状．6、（2010•）如图，在正方形网格中，△ABC 的三个顶点都在格点上，结合所给的平面直角坐标系解答以下问题：（1）将△ABC 向右平移5个单位长度，画出平移后的△A 1B 1C 1； （2）画出△ABC 关于X 轴对称的△A 2B 2C 2；（3）将△ABC 绕原点O 旋转180°，画出旋转后的△A 3B 3C 3； （4）在△A 1B 1C 1、△A 2B 2C 2、△A 3B 3C 3中，△_________与△_________成轴对称；△_________与△_________成中心对称．7、（2010•贵港）如下图，把△ABC 置于平面直角坐标系中，请你按以下要求分别画图： （1）画出△ABC 向下平移5个单位长度得到的△A 1B 1C 1；（2）画出△ABC 绕着原点O 逆时针旋转90°得到的△A 2B 2C 2； （3）画出△ABC 关于原点O 对称的△A 3B 3C 3．9、（2010•州）△ABC 在平面直角坐标系中的位置如下图． （1）作出△ABC 关于X 轴对称的△A 1B 1C 1，并写出点A 1的坐标； （2）作出将△ABC 绕点O 顺时针方向旋转180°后的△A 2B 2C 2．10、（2010•）△ABC 在平面直角坐标系中的位置如下图，将△ABC 沿Y 轴翻折得到△A 1B 1C 1，再将△A 1B 1C 1绕点O 旋转180°得到△A 2B 2C 2．请依次画出△A 1B 1C 1和△A 2B 2C 2． 13、（2010•）在小正方形组成的15×15的网络中，四边形ABCD 和四边形A ′B ′C ′D ′的位置如下图．（1）现把四边形ABCD 绕D 点按顺时针方向旋转90°，画出相应的图形A 1B 1C 1D 1， （2）若四边形ABCD 平移后，与四边形A ′B ′C ′D ′成轴对称，写出满足要求的一种平移方法，并画出平移后的图形A 2B 2C 2D 2．15、（2009•）在建立平面直角坐标系的方格纸中，每个小方格都是边长为1的小正方形，△ABC的顶点均在格点上，点P的坐标为（﹣1，0），请按要求画图与作答．（1）把△ABC绕点P旋转180°得△A′B′C′．（2）把△ABC向右平移7个单位得△A″B″C″．（3）△A′B′C′与△A″B″C″是否成中心对称，若是，找出对称中心P′，并写出其坐标．16、（2009•）如图，已知△ABC的三个顶点的坐标分别为A（﹣2，3）、B（﹣6，0）、C （﹣1，0）．（1）请直接写出点A关于Y轴对称的点的坐标；（2）将△ABC绕坐标原点O逆时针旋转90度．画出图形，直接写出点B的对应点的坐标；（3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．17、（2009•）如下图，每个小方格都是边长为1的正方形，以O点为坐标原点建立平面直角坐标系．（1）画出四边形OABC关于Y轴对称的四边形OA1B1C1，并写出点B1的坐标是_________；（2）画出四边形OABC绕点O顺时针方向旋转90°后得到的四边形OA2B2C2，并求出点C旋转到点C2经过的路径的长度．18、（2009•）如下图的正方形网格中，△ABC 的顶点均在格点上，在所给直角坐标系中解答以下问题：（1）分别写出点A 、B 两点的坐标；（2）作出△ABC 关于坐标原点成中心对称的△A 1B 1C 1；（3）作出点C 关于是X 轴的对称点P ．若点P 向右平移X 个单位长度后落在△A 1B 1C 1的部，请直接写出X 的取值围． 19、（2009•）如图，在每个小正方形的边长均为1个单位长度的方格纸中，有一个△ABC 和一点O ，△ABC 的顶点和点O 均与小正方形的顶点重合．（1）在方格纸中，将△ABC 向下平移5个单位长度得到△A 1B 1C 1，请画出△A 1B 1C 1； （2）在方格纸中，将△ABC 绕点O 旋转180°得到△A 2B 2C 2，请画出△A 2B 2C 2． 20、（2009•）如图，在下面的方格图中，将△ABC 先向右平移四个单位得到△A 1B 1C 1，再将△A 1B 1C 1绕点A 1逆时针旋转90°得到△A 1B 2C 2，请依次作出△A 1B 1C 1和△A 1B 2C 2．21、（2008•永春县）在边长为1的方格纸中建立直角坐标系XOY，O、A、B三点均为格点．（1）直接写出线段OB的长；（2）将△OAB绕点O沿逆时针方向旋转90°得到△OA′B′．请你画出△OA′B′，并求在旋转过程中，点B所经过的路径的长度．22、（2008•）如图，△AOB中，顶点A，B，O均在格点上，画出△AOB绕点O旋转180°后的三角形．（不要求写做法，证明，但要注明结果）23、（2008•）如图，菱形ABCD（图1）与菱形EFGH（图2）的形状、大小完全相同．（1）请从以下序号中选择正确选项的序号填写；①点E，F，G，H；②点G，F，E，H；③点E，H，G，F；④点G，H，E，F．如果图1经过一次平移后得到图2，那么点A，B，C，D对应点分别是_________；如果图1经过一次轴对称后得到图2，那么点A，B，C，D对应点分别是_________；如果图1经过一次旋转后得到图2，那么点A，B，C，D对应点分别是_________；（2）①图1，图2关于点O成中心对称，请画出对称中心（保留画图痕迹，不写画法）；②写出两个图形成中心对称的一条性质：_________．（可以结合所画图形表达）．24、（2008•眉山）如图，方格纸中△ABC的三个顶点均在格点上，将△ABC向右平移5格得到△A1B1C1，再将△A1B1C1绕点A1逆时针旋转180°，得到△A1B2C2．（1）在方格纸中画出△A1B1C1和△A1B2C2；（2）设B点坐标为（﹣3，﹣2），B2点坐标为（4，2），△ABC与△A1B2C2是否成中心对称？若成中心对称，请画出对称中心，并写出对称中心的坐标；若不成中心对称，请说明理由．25、（2008•）如下图，在网格中建立了平面直角坐标系，每个小正方形的边长均为1个单位长度，将四边形ABCD绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1．（1）直接写出D1点的坐标；（2）将四边形A1B1C1D1平移，得到四边形A2B2C2D2，若D2（4，5），画出平移后的图形．（友情提示：画图时请不要涂错阴影的位置哦！）26、（2008•来宾）如图，已知△ABC关于直线MN的对称图形是△A1B1C1，将△A1B1C1绕点A1逆时针旋转90°得到△A1B2C2．请在图中分别画出△A1B1C1和△A1B2C2，并正确标出对应顶点的字母．（不要求写出画法）27、（2008•）在如下图出方格纸中，每个小正方形的边长都为1．（1）画出将铅笔图形ABCDE向上平移9格得到的铅笔图形A1B1C1D1E1；（2）将铅笔图形A1B1C1D1E1，绕点A1，逆时针旋转90°，画出转后的铅笔图形A1B2C2D2E2．28、（2008•）如图，在平面直角坐标系中，△ABC和△A1B1C1关于点E成中心对称．（1）画出对称中心E，并写出点E、A、C的坐标；（2）P（a，b）是△ABC的边AC上一点，△ABC经平移后点P的对应点为P2（a+6，b+2），请画出上述平移后的△A2B2C2，并写出点A2、C2的坐标；（3）判断△A2B2C2和△A1B1C1的位置关系．（直接写出结果）29、（2008•）△ABC在平面直角坐标系中的位置如下图．（1）将△ABC向右平移6个单位得到△A1B1C1，请画出△A1B1C1；并写出点C1的坐标；（2）将△ABC绕原点O旋转180°得到△A2B2C2，请画出△A2B2C2．30、（2008•）已知：如图，在8×12的矩形网格中，每个小正方形的边长都为1，四边形ABCD的顶点都在格点上．（1）在所给网格中按以下要求画图：①在网格中建立平面直角坐标系（坐标原点为O），使四边形ABCD各个顶点的坐标分别为A（﹣5，0）、B（﹣4，0）、C（﹣1，3）、D（﹣5，1）；②将四边形ABCD沿坐标横轴翻折180°，得到四边形A′B′C′D′，再把四边形A′B′C′D′绕原点O旋转180°，得到四边形A″B″C″D″；（2）写出点C″、D″的坐标；（3）请判断四边形A″B″C″D″与四边形ABCD成何种对称？若成中心对称，请写出对称中心；若成轴对称，请写出对称轴．答案与评分标准一、解答题（共30小题）1、（2010•）如图，在边长为1的小正方形组成的网格中，△AOB的三个顶点均在格点上，点A、B 的坐标分别为A（﹣2，3）、B（﹣3，1）．（1）画出坐标轴，画出△AOB绕点O顺时针旋转90°后的△A1OB1；（2）点A1的坐标为（3，2）；（3）四边形AOA1B1的面积为8．考点：作图-旋转变换。

第2课时旋转作图及变换知识点1.图形旋转的性质是：(1)旋转前后的图形；(2)对应点到旋转中心的距离；(3)对应点与旋转中心所连线段的夹角等于2.简单的旋转作图---旋转作图的步骤（1）确定旋转；（2）找出图形的关键点；（3）将图形的关键点与旋转中心连接起来，然后按旋转方向分别将它们旋转一个角，得到此关键点的对应点；(4)按图形的顺序连接这些对应点，所得到的图形就是旋转后的图形。

一、选择题1．在图形旋转中，下列说法错误的是（）A．在图形上的每一点到旋转中心的距离相等B．图形上每一点移动的角度相同C．图形上可能存在不动的点D．图形上任意两点的连线与其对应两点的连线长度相等2．如图，下面的四个图案中，既包含图形的旋转，又包含图形的轴对称的是（）3.如图所示的图案绕旋转中心旋转后能够与自身重合，那么它的旋转角可能是（）。

A.60°B.90°C.72°D.120°4．如图，摆放有五杂梅花，下列说法错误的是（以中心梅花为初始位置）（• ）A．左上角的梅花只需沿对角线平移即可B．右上角的梅花需先沿对角线平移后，再顺时针旋转45°C．右下角的梅花需先沿对角线平移后，再顺时针旋转180D．左下角的梅花需先沿对角线平移后，再顺时针旋转90°5 △ABC绕着A 点旋转后得到△AB′C′，若∠BAC′=130°，∠BAC=80°，•则旋转角等于（）A．50° B．210° C．50°或210° D．130°二、填空题6．图形的平移、旋转、轴对称中，其相同的性质是_________.7．如图，△ABC和△ADE均是顶角为42°的等腰三角形，BC、DE分别是底边，图中的△ABD绕A旋转42°后得到的图形是________，它们之间的关系是______，•其中BD=_________．8、如图，将△OAB绕点0按逆时针方面旋转至△0A′B′，使点B恰好落在边A′B′上．已知AB=4cm，BB′=lcm，则A′B长是_______cm．9、如图，在平面直角坐标系中，点A的坐标为(1，4)，将线段O A绕点O顺时针旋转90°得到线段OA′，则点A′的坐标是___________. 10．如图，自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F，•∠EAF=45°，在保持∠EAF=45°的前提下，当点E、F分别在边BC、CD上移动时，BE+•DF•与EF的关系是________．11.如图，在直角坐标系中，已知点)0,3(A、)4,0(B，对△OAB 连续作旋转变换，依次得到三角形①、②、③、④…，则三角形⑩的直角顶点的坐标为__________．三、综合提高题12.观察下列图形，它可以看作是什么“基本图形”通过怎样的旋转而得到的？13.如图：若∠AOD=∠BOC=60°,A、O、C三点在同一条线上，△AOB与△COD 是能够重合的图形。

3.4简单的旋转作图习题精选一1．如图，把绕O点逆时针旋转120°、240°，试一试画出的图形是怎样的图形．2．如图，画出长方形ABCD绕点C顺时针旋转120°所得到的图形．3．如图，画出绕点O顺时针旋转100°所得到的图形．4．如图，你能把圆O绕P点顺时针旋转90°吗？5．圈出图中的“基本图案”，说明这些美丽的图案都是怎样旋转得到的？6．图中的六边形中“基本图案”是怎样旋转而成下列图形的？7．把下面几个图形中左上角的图案绕着中心旋转90°，180°，270°，画出所得图案。

8．观察图，圈中其中的“基本图案”，说明它是怎样由“基本图案”旋转而成的．参考答案1．2．3．如下图4．如上图5．（1）一个花瓣顺时针旋转90°，180°，270°（2）螺旋桨的一半旋转180°（3）雪花顺时针旋转60°，120°，180°，240°，300°（4）一个猴子旋转180°（5）一个熊猫旋转90°，180°，270°（6）一只鸽子旋转180°画图：略．6．（1）（2）（3）中“基本图案”分别旋转60°，120°，180°，240°，300°（4）中“基本图案”旋转120°，240°．7．略．8．把“基本图案”顺时针旋转60°，120°，180°，240°，300°而成．二1．在图书、杂志、报纸、包装盒、广告单等处寻找几个旋转对称图形的实例．2．如图，非等腰三角板原在ABC的位置上，旋转后到了的位置上，请指出旋转中心、旋转角度和旋转方向．3．已知（如图），请画出以C点为旋转中心，旋转角为30°，（1）按顺时针方向旋转后的图形；（2）按逆时针方向旋转后的图形．4．下列各图形围绕自己的旋转中心最低需要旋转多少度之后，能够与它自身相重合？5．如图，下列各图形，不是旋转对称图形的是（）6．如图，正方形ABCD，画出绕顶点C顺时针旋转90°后的图形．7．画一个三角形，使通过这个三角形的旋转得到一个正方形，指出这是一个什么三角形，旋转中心是什么，每次旋转的角度，需要旋转多少次才能完成这个图形．8．如图，以线段CD外的点A为旋转中心，按逆时针方向旋转120°，请画出图形．9．如图，已知点A、B，以A为旋转中心逆时针旋转30°，B点到达；继续旋转60°到；再继续旋转90°到；再继续旋转120°到．请画出多边形．10．图中给出的是一个数轴，以原点O为旋转中心，逆时针旋转90°．画图形，连同单位和标数一齐标注上．11．在图中，画出以O点为旋转中心，顺时针旋转90°后所得到的图形．12．画一个三角形，使通过这个三角形的旋转能得到一个正五边形，指出旋转中心、旋转的次数和每次旋转的角度．13．如图，已知平行四边形ABCD，画出以平行四边形对角线交点O为旋转中心顺时针旋转90°后所得到的图形．参考答案1．略．2．旋转中心是点A，旋转角度为30°，旋转方向为顺时针．3．见答图．4．（1）60°；（2）20°；（3）90°．5．D6．答图中的是旋转后的正方形．7．见答图．三角形为等腰直角三角形，直角顶点A为旋转中心，每次转90°，转4次．8．见答图．连结AC、AD，以A为旋转中心将A C、AD分别逆时针旋转120°，得，则即由CD旋转而成．9．见答图．10．见答图．这个由两个互相垂直的数轴所构成的图形叫做平面直角坐标系．它是一个很用的数学工具，在以后的数学学习中会经常用到．11．见答图．12．见答图．这个三角形是一个顶角为72°的等腰三角形，旋转中心为顶点A，旋转次数为5次，每次旋转的角度为360°÷5＝72°．13．见答图（顺时针旋转两条对角线，使转过的角度为90°）．。