简单的旋转作图
- 格式:ppt
- 大小:746.50 KB
- 文档页数:3

CAD中利用旋转轴进行图形旋转与对称CAD软件是计算机辅助设计软件的缩写,它在工程设计中起到了举足轻重的作用。
在CAD软件中,利用旋转轴进行图形旋转和对称是一项非常重要的技巧。
本文将介绍如何在CAD中使用旋转轴实现图形旋转和对称。
首先,我们需要了解旋转轴的概念。
旋转轴是一个以一点为中心的直线段,用于将图形进行旋转。
在CAD中,我们可以通过选择图形的中心点和一个与之垂直的直线段来定义旋转轴。
在CAD软件中,进行图形旋转和对称的操作步骤如下:1. 打开CAD软件并新建一个文件。
2. 在绘图界面中选择需要旋转或对称的图形。
可以使用绘图工具(如直线、圆等)绘制一个图形,或者导入已有图形。
3. 点击“编辑”或“修改”选项卡,找到“旋转”命令,并点击打开该命令。
4. 在弹出的旋转对话框中,先选择需要旋转的图形。
然后,选择一个合适的旋转轴。
在选择旋转轴时,可以选择图形特征点作为旋转轴的一部分。
5. 输入旋转的角度。
根据需要,可以输入具体的角度或者选择图形的参考点,并指定旋转的角度。
6. 点击“确定”按钮完成旋转操作。
此时,选定的图形将根据旋转轴和角度进行旋转。
要实现图形的对称,可以借助旋转轴来实现。
下面是使用旋转轴进行对称的步骤:1. 打开CAD软件并新建一个文件。
2. 在绘图界面中选择需要进行对称操作的图形。
可以使用绘图工具绘制一个图形,或者导入已有图形。
3. 点击“编辑”或“修改”选项卡,找到“旋转”命令,并点击打开该命令。
4. 在弹出的旋转对话框中,选择需要对称的图形。
然后,选择一个合适的旋转轴。
在选择旋转轴时,需要注意选择一个与对称轴垂直的直线段。
5. 输入旋转的角度。
根据需要,可以输入具体的角度或者选择图形的参考点,并指定旋转的角度。
对于对称操作,一般选择180度,即沿选定的旋转轴进行对称。
6. 点击“确定”按钮完成对称操作。
此时,选定的图形将根据旋转轴进行镜像对称。
通过上述步骤,我们可以在CAD中利用旋转轴进行图形的旋转和对称。

2019年八年级数学下册第四章简单的旋转作图教案北师大版一、学生起点分析学生已对轴对称、平移这两种简单的全等变换有了很好的认识,并对旋转有了初步的了解。
教材将旋转变换安排至此,目的是力求让学生从动态的角度观察图形、分析问题,为将来掌握“全等”知识奠定基础。
由于旋转与轴对称、平移都是全等变换,在特征上既存在共性又有特性;而学生已经掌握了轴对称、平移的特征,因此,探索、理解旋转区别于轴对称、平移的特征成了本节课学习的重要任务。
二、教学任务分析本节课的主要内容是通过实例进一步认识旋转变换,探索、理解旋转的特征,并应用旋转的特征作图、解决简单的图形问题。
教学目标知识目标:1.简单平面图形旋转后的图形的作法.2.确定一个三角形旋转后的位置的条件.能力训练:1.对具有旋转特征的图形进行观察、分析、画图和动手操作等过程,掌握画图技能.2.能够按要求作出简单平面图形旋转后的图形.情感与价值观:1.通过画图,进一步培养学生的动手操作能力.2.对具有旋转特征的图形进行观察、分析、画图过程中,进一步发展学生的审美观念. 教学重点:简单平面图形旋转后的图形的作法.教学难点:简单平面图形旋转后的图形的作法.三、教学过程设计第一环节巧设情境问题,引入课题1.下列一组图形变换属于旋转变换的是()2.大家来看一面小旗子(出示小旗子,然后一边演示一边叙述),把这面小旗子绕旗杆底端旋转90°后,这时小旗子的位置发生了变化,形成了新的图案,你能把这时的图案画出来吗?在原图上找了四个点,即O 点、A 点、B 点、C 点,如图(教师把该生所画的图在投影上放影)这四个点是表示这面小旗子的关键点.因为旋转前后两个图形的对应点到旋转中心的距离相等,对应点与旋转中心的连线所组成的旋转角彼此相等,所以根据已知:要把这面小旗绕O 点按顺时针旋转90°.我在方格中找到点A ,B ,C 的对应点A ′,B ′,C ′,然后连接,就得到了所求作的图形.作图的一个要点:找图形的关键点。


简单的旋转作图一、教学目标:1.经历对具有旋转特征的图形进行观察、分析、动手操作和画图等过程,掌握画图技能。
2.能够按要求作出简单平面图形旋转后的图形。
二、教学重点:寻找旋转中心三、教学难点:按旋转角相等作图四、课型/课时:新课 1五、教学用具:三角尺、圆规六、教学方法:演讲法、探究法七、教学内容:1.引入课题如图,在方格纸上作出“小旗子”绕O点按顺时针旋转090后的图案,并简述理由。
//C/A所在位置为旋转后“小旗子”的位置B2.例题例1.如图,ABC绕C点旋转后顶点A的对应点为点D,试确定顶点B对应点的位置以及旋转后的三角形。
分析:假设顶点B 的对应点为点E ,则AC E BC E ∠∠,都是旋转角,且CE=CB,CD=CA 。
解: (1).连接CD(2).如图2,以BC 为边作A CD B CE ∠=∠∠使得BCE(3).在射线CF 上截取CE=CB(4).连接DE D C E ∆就是ABC ∆绕C 点旋转后的图形。
议一议 你还能用其他方法作出例1中的DEC ∆吗?解:先连接CD ,再分别以C 、D 为圆心,以CB 、AB 的长为半径画弧得到交点E ,连接CE 、DE 即可得到DEC , DEC ∆∆就是ABC ∆绕C 点旋转后的图形。
想一想在旋转过程中,确定一个三角形旋转后的位置,除需要此三角形原来的位置外,还需要什么条件。
解:(1)旋转中心(图形上和图形外)(2)旋转角(3)旋转方向随堂练习在下图中,将大写字母N饶它右下侧的顶点按顺时针方向旋转90,做出旋转后的图案。
解:先确定字母N的四个顶点,绕它右下侧的顶点按顺时针方向旋转090后的位置,然后连线即可。
八.作业设计知识技能1、 2。

教学反思
23.1.2旋转对称图形及简单的旋转作图
(新授课)
1.成功之处
本节课重点是要让学生了解图形的旋转运动,明确旋转中心、旋转角等概念,掌握简单图形的旋转的作图方法。
为了让智障学生了解这种运动,教学中可多添加生活中的实例图形,使他们能从浅显的物体运动体会出抽象的图形的运动。
旋转运动在我们的生活中无处不在,客观存在的事物,我们要尽其所能地研究其规律,通过简单的几何图形的旋转运动,让学生了解到这一运动的一些特征,亦是为学生后阶段的学习打下良好的基础。
2.需注意的几个问题:
(1)注意师生互动,提高学生的思维效率.
(2)针对学生的盲区,出相应的练习巩固.
最后,在今后的教学中,及时找出课堂上出现的共性问题,利用辅导课上及时纠正,然后做针对性练习来巩固盲区,强化课堂薄弱环节,使课堂走向优质高效化.。

第三章图形的平移与旋转一、平移定义和规律1平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.关键:a. 平移不改变图形的形状和大小(也不会改变图形的方向,但改变图形的位置)。
b. 图形平移三要素:原位置、平移方向、平移距离。
2平移的规律(性质):经过平移,对应点所连的线段平行且相等,对应线段平行且相等、对应角相等。
注意:平移后,原图形与平移后的图形全等。
3简单的平移作图:平移作图要注意:①方向;②距离。
整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动。
二、旋转的定义和规律1旋转的定义:在平面内,将一个图形饶一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
这个定点称为旋转中心;转动的角称为旋转角.关键:a。
旋转不改变图形的形状和大小(但会改变图形的方向,也改变图形的位置)。
b。
图形旋转四要素:原位置、旋转中心、旋转方向、旋转角。
2旋转的规律(性质):经过旋转,图形上的每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.(旋转前后两个图形的对应线段相等、对应角相等。
)注意:旋转后,原图形与旋转后的图形全等.3简单的旋转作图:旋转作图要注意:①旋转方向;②旋转角度。
整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动。
三、中心对称1.中心对称的有关概念:中心对称、对称中心、对称点把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称,这个点叫做对称中心,两个图形中的对应点叫做对称点。
2.中心对称的基本性质:(1).成中心对称的两个图形具有图形旋转的一切性质。
(2).成中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。
3.中心对称图形的有关概念:中心对称图形、对称中心把一个平面图形绕某一点旋转180°,如果旋转后的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形.这个点就是它的对称中心。

3.生活中的旋转4.简单的旋转作图班级:___________________________姓名:___________________________作业导航理解图形旋转的意义,掌握图形旋转的性质,会进行简单的旋转作图,能够观察发现生活中的图形旋转现象.一、选择题1.平面图形的旋转一般情况下改变图形的( )A.位置B.大小C.形状D.性质2.9点钟时,钟表的时针和分针之间的夹角是( )A.30°B.45°C.60°D.90°3.将平行四边形ABCD 旋转到平行四边形A ′B ′C ′D ′的位置,下列结论错误的是( )A.AB =A ′B ′B.AB ∥A ′B ′C.∠A =∠A ′D.△ABC ≌△A ′B ′C ′二、填空题4.钟表上的指针随时间的变化而移动,这可以看作是数学上的_______.5.菱形ABCD 绕点O 沿逆时针方向旋转到四边形D C B A '''',则四边形D C B A ''''是__________.6.△ABC 绕一点旋转到△A ′B ′C ′,则△ABC 和△A ′B ′C ′的关系是_______.7.钟表的时针经过20分钟,旋转了_______度.8.图形的旋转只改变图形的_______,而不改变图形的_______.三、解答题9.下图中的两个正方形的边长相等,请你指出可以通过绕点O 旋转而相互得到的图形并说明旋转的角度.10.在图中,将大写字母H 绕它右上侧的顶点按逆时针方向旋转90°,请作出旋转后的图案.11.如图,菱形A ′B ′C ′D ′是菱形ABCD 绕点O 顺时针旋转90°后得到的,你能作出旋转前的图形吗?12.Rt△ABC,绕它的锐角顶点A分别逆时针旋转90°、180°和顺时针旋转90°,(1)试作出Rt△ABC旋转后的三角形;(2)将所得的所有三角形看成一个图形,你将得到怎样的图形?13.如图,将右面的扇形绕点O按顺时针方向旋转,分别作出旋转下列角度后的图形:(1)90°;(2)180°;(3)270°.你能发现将扇形旋转多少度后能与原图形重合吗?14.如图,分析图中的旋转现象,并仿照此图案设计一个图案.3.生活中的旋转4.简单的旋转作图一、1.A 2.D 3.B二、4.旋转 5.菱形 6.全等7.10 8.位置形状和大小三、9.△OAE和△OBF,△OEB和△OFC,△OAB和△OBC,旋转的角度为90°10~14.略。

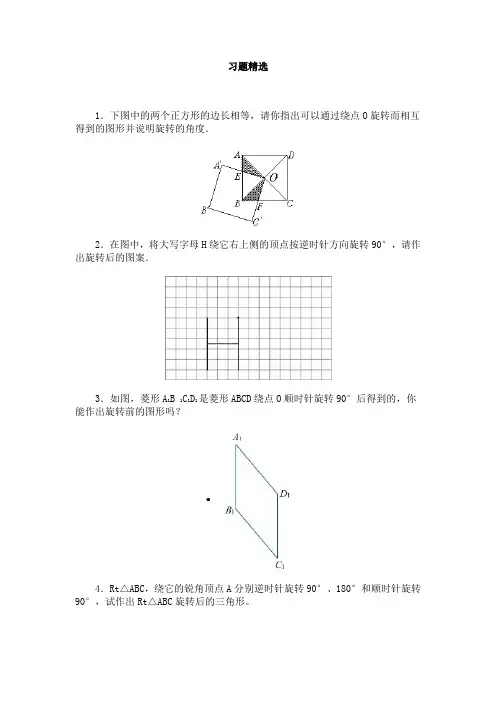
习题精选
1.下图中的两个正方形的边长相等,请你指出可以通过绕点O旋转而相互得到的图形并说明旋转的角度.
2.在图中,将大写字母H绕它右上侧的顶点按逆时针方向旋转90°,请作出旋转后的图案.
3.如图,菱形A
1B
1
C
1
D
1
是菱形ABCD绕点O顺时针旋转90°后得到的,你
能作出旋转前的图形吗?
4.Rt△ABC,绕它的锐角顶点A分别逆时针旋转90°、180°和顺时针旋转90°,试作出Rt△ABC旋转后的三角形。
5.如图,将右面的扇形绕点O按顺时针方向旋转,分别作出旋转下列角度后的图形:
(1)90°;(2)180°;(3)270°.
你能发现将扇形旋转多少度后能与原图形重合吗?
参考答案:
1.△OAE和△OBF,△OEB和△OFC,△OAB和△OBC,旋转的角度为90°
2.图中黄色“H”即为旋转后的图案
3.下图中黄色菱形即为旋转前的
4.(1)图①中粉色三角形ΔAB
1C
1
即ΔABC逆时针旋转90º后的图形;图②
中蓝色三角形ΔAB
2C
2
即ΔABC逆时针旋转180º后的图形;图③中黄色三角形Δ
AB
3C
3
即ΔABC顺时针旋转90º后的图形
5.
旋转360º后与原图形重合。

