旋转作图题训练题

23.1 图形的旋转旋转的概念将一个图形绕一个定点转动一定的角度，这样的图形运动称为图形的旋转.定点称为旋转中心，旋转的角度称为旋转角.注意：旋转的三要素：旋转中心、旋转方向和旋转角度；图形的旋转不改变图形的形状、大小.题型1：旋转中的概念及对应元素1.下列运动中，属于旋转运动的是（ ）A．小明向北走了4 米B．一物体从高空坠下C．电梯从1 楼到12 楼D．小明在荡秋千【答案】D【解析】【解答】解：A. 小明向北走了 4 米，是平移，不属于旋转运动，A不合题意；B. 一物体从高空坠下，是平移，不属于旋转运动，B不合题意；C. 电梯从1 楼到12 楼，是平移，不属于旋转运动，C不合题意；D. 小明在荡秋千，是旋转运动，D符合题意．故答案为：D．【分析】根据图形旋转的定义求解即可。

【变式1-1】如图，线段AB绕着点O旋转一定的角度得线段A'B'，下列结论错误的是（ ）A．AB＝A'B'B．∠AOA'＝∠BOB'C．OB＝OB'D．∠AOB'＝100°【答案】D【解析】【解答】∵线段AB绕着点O旋转一定的角度得线段A'B'，∴AB＝A′B′，∠AOA′＝BOB′，OB＝OB′，故A，B，C选项正确，∵∠AOB和∠BOB′的度数不确定，∴∠AOB′≠100°，故D选项错误.故答案为：D.【分析】由旋转的性质可得AB＝A′B′，∠AOA′＝BOB′，OB＝OB′，据此判断.【变式1-2】如图（1）中，△和△都是等腰直角三角形，∠和∠都是直角，点在上，△绕着点经过逆时针旋转后能够与△重合，再将图（1）作为“基本图形”绕着点经过逆时针旋转得到图（2）.两次旋转的角度分别为（ ）A．45°，90°B．90°，45°C．60°，30°D．30°，60°【答案】A【解析】根据图1可知，∵△ABC和△ADE是等腰直角三角形，∴∠CAB=45°，即△ABC绕点A逆时针旋转45°可到△ADE；如右图，∵△ABC和△ADE是等腰直角三角形，∴∠DAE=∠CAB=45°，∴∠FAB=∠DAE+∠CAB=90°，即图1可以逆时针连续旋转90°得到图2．故选A．旋转的性质一个图形和它经过旋转所得到的图形中：(1)对应点到旋转中心的距离相等； (2)两组对应点分别与旋转中心连线所成的角相等.　注意：图形绕某一点旋转，既可以按顺时针旋转也可以按逆时针旋转.题型2：旋转的性质及旋转中心的确定2.如图，△DEF是由△ABC绕着某点旋转得到的，则这点的坐标是( )A．(1，1)B．(0，1)C．(-1，1)D．(2，0)【答案】B【解析】【解答】解：如图，连接AD、BE，作线段AD、BE的垂直平分线，两线的交点即为旋转中心O′.其坐标是(0，1).故答案为：B.【分析】连接AD、BE，作线段AD、BE的垂直平分线，根据旋转的性质即可求解。

小升初数学专项练习一线名师严选内容，逐一攻克☆基本概念、基本原理、基础技能一网打尽☆点拨策略思路，侧重策略指导，拓宽眼界思路☆4.作旋转一定角度后的图形【小升初考点归纳】1．旋转作图步骤：（1）明确题目要求：弄清旋转中心、旋转方向和旋转角；（2）分析所作图形：找出构成图形的关键点；（3）找出关键点的对应点：按一定的方向和角度分别作出各关键点的对应点；（4）作出新图形：顺次连接作出的各点．（5）写出结论：说明作出的图形．2．中心对称作图步骤：（1）连接原图形上的所有特殊点和对称中心；（2）再将以上连线延长找对称点，使得特殊点与对称中心的距离和对称点与对称中心的距离相等；（3）将对称点按原图形的形状顺次连接起来，即可得出关于对称中心对称的图形．【经典例题】一．选择正确的答案，把序号填在括弧中（共1小题）1．（2016•长沙模拟）下面图形中，以某一边为轴旋转一周，可以得到圆锥的是（）A．B．C．D．【解析】解：直角三角形沿一条直角边旋转一周得到的几何体是一个圆锥．故选：A．二．操作题（共14小题）2．（2019春•南京月考）（1）将先向下平移5格，再向右平移13格．（2）将平行四边形沿A点顺时针方向旋转90°．【解析】解：（1）将先向下平移5格（下图红色部分），再向右平移13格（下图绿色部分）：（2）将平行四边形沿A点顺时针方向旋转90°（下图蓝色部分）：3．（2019春•枣阳市校级月考）（1）将图形A绕点O点顺时针旋转90°得到的图形B．（2）将图形B向右平移4格得到图形C．【解析】解：（1）将图形A绕点O点顺时针旋转90°得到的图形B（下图）：（2）将图形B向右平移4格得到图形C（下图）：4．（2018•泉州）（1）按要求画图．①将图中的三角形①绕O点顺时针旋转90°，画出旋转后的图形②．②将图中的三角形①平移，使平移后的三角形顶点O的位置在（9，5），画出平移后的图形③．【解析】解：根据分析可得，5．（2018春•新罗区期末）画一画：（1）把图形绕点O逆时针旋转90°．（2）把旋转后的图形向下平移两格．【解析】解：6．（2018•漳平市校级模拟）做一做，画一画（1）画出图形A的另一半，使它成为一个以直线a为对称轴的对称图形．（2）画出把图形B向右平移6格后得到的图形．（3）画出把图形C绕O点顺时针旋转90°后得到的图形．（4）用数对表示O点的位置是（8，6）．【解析】解：（1）画出图形A的另一半，使它成为一个以直线a为对称轴的对称图形．（2）画出把图形B向右平移6格后得到的图形．（3）画出把图形C绕O点顺时针旋转90°后得到的图形．（4）用数对表示O点的位置是（8，6）．故答案为：8，6．7．（2018春•隆化县校级期末）画出三角形AOB绕O点逆时针旋转180o后的图形．【解析】解：画出三角形AOB绕O点逆时针旋转180°后的图形（图中红色部分）：8．（2018春•卢龙县期中）画出三角形AOB绕点O逆时针旋转90度的图形．【解析】解：画出三角形AOB绕点O逆时针旋转90度的图形（图中红色部分）：9．（2018秋•廉江市期中）画出三角形AOB绕B点顺时针旋转90度后的图形．【解析】解：作图如下：10．（2018•兴仁县）按要求画一画．（1）画出图形A向右平移5格后得到的图形B．（2）画出图形B绕点O逆时针旋转90°后得到的图形C．【解析】解：（1）画出图形A向右平移5格后得到的图形B（下图）：（2）画出图形B绕点O逆时针旋转90°后得到的图形C（下图）：11．（2017春•海南区期末）画出三角形AOB绕O点顺时针旋转90度后的图形．【解析】解：根据题干分析画图如下：12．（2016春•洛阳月考）将长方形绕A点顺时针旋转90°．【解析】解：将长方形绕A点顺时针旋转90°（图中红色部分）：13．（2016春•新郑市校级月考）画出下面的图象中的三角形沿着A点顺时针旋转90度后的图形．【解析】解：三角形沿着A点顺时针旋转90度后的图形（红色部分）：14．（2016秋•永州期中）把如图的小三角旗绕点A沿顺时针方向旋转90度．再向右平移4格．分别画出旋转和平移后的图形．【解析】解：画图如下：15．（2016春•南海区期末）画出面积是3平方厘米的三角形AOB并绕O点逆时针旋转180o 后的图形．【解析】解：根据题干分析可得：三．解析题（共7小题）16．（2019春•东海县月考）按要求画一画．①将长方形绕A点逆时针旋转90°．②将小旗围绕B点逆时针旋转90°．【解析】解：作图如下：17．（2019春•古浪县校级期末）先将△ABC绕点C点顺时针旋转90°得到△A′B′C，再将△A′B′C′向下平移4格．【解析】解：先将△ABC绕点C点顺时针旋转90°得到△A′B′C，再将△A′B′C′向下平移4格．18．（2018春•抚宁区期末）画出绕点“O”顺时针旋转90度后的图形．【解析】解：作图如下：19．（2017秋•保定期末）画出三角形逆时针旋转90度后的图形．【解析】解：作图如下：20．（2018春•桃城区校级期末）（1）小鱼图从右下方移至左上方，先向上平移3格，又向左平移5格．（2）把梯形绕A点顺时针方向旋转90°，画出旋转后的图形．【解析】解：（1）根据题干分析可得：小鱼图从右下方移至左上方，先向上平移3格，再向左平移5格；（2）根据分析画图如下：故答案为：上、3、左、5．21．（2017春•绍兴期末）画出三角形AOB绕O点顺时针旋转90°后的图形．【解析】解：画出三角形AOB绕O点顺时针旋转90°后的图形：22．（2017春•绍兴期末）画出三角形AOB绕O点顺时针旋转90°后的图形．【解析】解：画出三角形AOB绕O点顺时针旋转90°后的图形：。

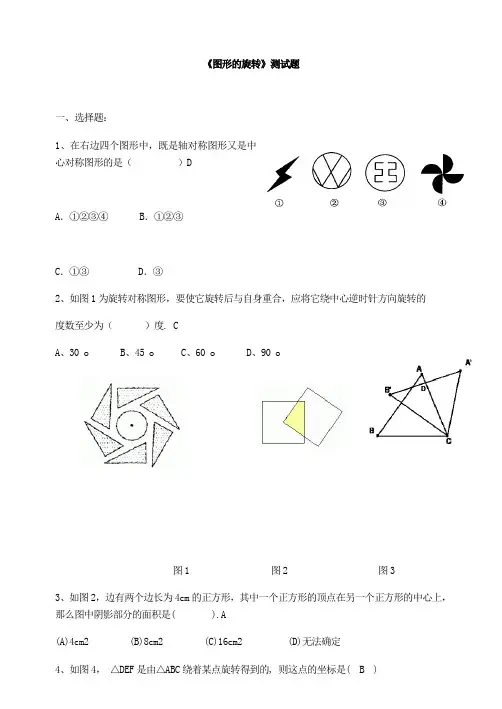
《图形的旋转》测试题一、选择题：1、在右边四个图形中，既是轴对称图形又是中心对称图形的是（）DA．①②③④ B．①②③C．①③ D．③2、如图1为旋转对称图形，要使它旋转后与自身重合，应将它绕中心逆时针方向旋转的度数至少为（）度. CA、30 oB、45 oC、60 oD、90 o图1 图2 图33、如图2，边有两个边长为4cm的正方形，其中一个正方形的顶点在另一个正方形的中心上，那么图中阴影部分的面积是( ).A(A)4cm2 (B)8cm2 (C)16cm2 (D)无法确定4、如图4，△DEF是由△ABC绕着某点旋转得到的, 则这点的坐标是( B )图5 图4 A. (1,1) B. (0,1) C. (−1,1) D. (2,0)二、填空题5、点a 4（，）与3b （，）关于原点对称，则a b += .-76、如图3，把三角形△ABC 绕着点C 顺时针旋转350，得到△A ＇B ＇C ，A ＇B ＇交AC 于点D ，若∠A ＇DC=900，则∠A 的度数是__________。

5507、如图5， △ABC 中, (ACB = 90(, (B = 30(, BC = 6, 三角板绕C 逆时针旋转, 当点A的对应点A' 落在AB 边上时即停止转动, 则BM 的长为 3 .8、如图6，△ABC 中, 已知∠C=90°, ∠B=50°, 点D 在边BC 上, BD=2CD. 把△ABC 绕着点D逆时针旋转m （0(<m<180(）度后, 如果点B 恰好落在初始Rt △ABC 的边上, 那么m = _______.80(或120(.三、解答题9、作图题（1）如图7，画出△ABC 绕点O 顺时针旋转60°所得到的图形．图6 BA CO图7 图8（2）如图8,在直角坐标系中,点P 的坐标为(3,4),将OP 绕原点O 逆时针旋转90°得到线段OP ′,(1)在图中画出线段OP ′;(2)P ′的坐标为 ______. (-4,3)1、如图，在△ABC 中，∠B=900，∠C=300，AB=1，将△ABC 绕顶点A 旋转1800，点C 落在C1处，则C C1的长为（ ）A ．24B ．4C ．32D ．522、如图，△ABC 中，∠ACB=1200，将它绕着点C 旋转300 后得到△DCE ，则∠ACE=∠A+∠E=3、如图，在Rt △ABC 中，∠ACB=90°，∠A=35°，以直角顶点C•为旋转中心，将△ABC 旋转到△A ′B ′C 的位置，其中A ′、B ′分别是A 、B 的对应点，且点B 在斜边A ′B ′上，直角边CA ′交AB 于D ，求∠BDC 的度数．4，如图，正方形ABCD 中，E 在BC 上，F 在AB 上且∠FDE=45°，•△DEC 按顺时针方向转动一个角度后成为△DGA ．（1）图中哪一个点是旋转中心？（2）旋转了多少度？（3）指出图中的对应点，对应线段和对应角；（4）求∠GDF 的度数．5、已知如图，正方形ABCD 中，E 为CD 边上一点，F 为BC 边上一点，CE=CF:(1)EBC FDC ∠∠与相等吗？（2）△DCF 能与△BCE 重合吗？（3）试判断BE 与DF 的位置关系并说明理由,6．如图所示，四边形ABCD 中，∠BAD=∠C=90°，AB=AD ，AE ⊥BC 于E ，△BEA 旋转后能与△DFA 重合．（1）旋转中心是哪一点？（2）旋转了多少度？（3）若AE=5cm ，求四边形ABCD 的面积．7，如图，K是正方形ABCD内一点，以AK为一边作正方形AKLM，使L，M，D在AK的同旁，连结BK和DM，试用旋转的思想说明线段BK与DM的关系．,8，.如图所示，等边△ABC中，D是AB边上的动点(不与A、B重合)，以CD为一边，向上作等边△EDC。

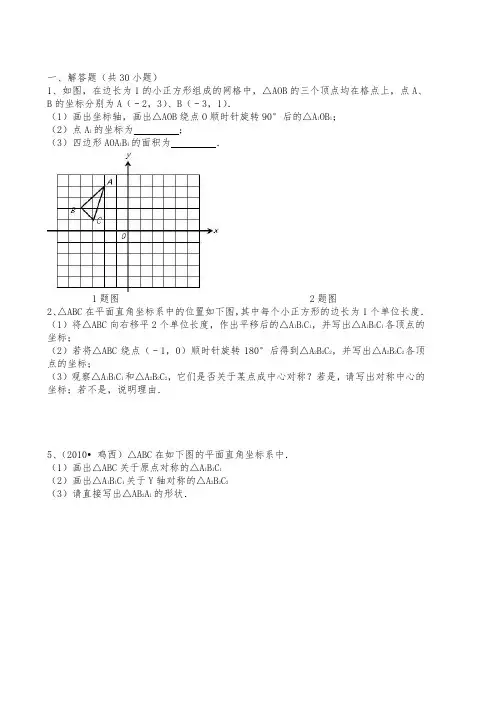
一、解答题（共30小题）1、如图，在边长为1的小正方形组成的网格中，△AOB的三个顶点均在格点上，点A、B的坐标分别为A（﹣2，3）、B（﹣3，1）．（1）画出坐标轴，画出△AOB绕点O顺时针旋转90°后的△A1OB1；（2）点A1的坐标为_________；（3）四边形AOA1B1的面积为_________．1题图 2题图2、△ABC在平面直角坐标系中的位置如下图，其中每个小正方形的边长为1个单位长度．（1）将△ABC向右移平2个单位长度，作出平移后的△A1B1C1，并写出△A1B1C1各顶点的坐标；（2）若将△ABC绕点（﹣1，0）顺时针旋转180°后得到△A2B2C2，并写出△A2B2C2各顶点的坐标；（3）观察△A1B1C1和△A2B2C2，它们是否关于某点成中心对称？若是，请写出对称中心的坐标；若不是，说明理由．5、（2010•鸡西）△ABC在如下图的平面直角坐标系中．（1）画出△ABC关于原点对称的△A1B 1 C1（2）画出△A1B1C1关于Y轴对称的△A2B2C2（3）请直接写出△AB2A1的形状．6、（2010•）如图，在正方形网格中，△ABC 的三个顶点都在格点上，结合所给的平面直角坐标系解答以下问题：（1）将△ABC 向右平移5个单位长度，画出平移后的△A 1B 1C 1； （2）画出△ABC 关于X 轴对称的△A 2B 2C 2；（3）将△ABC 绕原点O 旋转180°，画出旋转后的△A 3B 3C 3； （4）在△A 1B 1C 1、△A 2B 2C 2、△A 3B 3C 3中，△_________与△_________成轴对称；△_________与△_________成中心对称．7、（2010•贵港）如下图，把△ABC 置于平面直角坐标系中，请你按以下要求分别画图： （1）画出△ABC 向下平移5个单位长度得到的△A 1B 1C 1；（2）画出△ABC 绕着原点O 逆时针旋转90°得到的△A 2B 2C 2； （3）画出△ABC 关于原点O 对称的△A 3B 3C 3．9、（2010•州）△ABC 在平面直角坐标系中的位置如下图． （1）作出△ABC 关于X 轴对称的△A 1B 1C 1，并写出点A 1的坐标； （2）作出将△ABC 绕点O 顺时针方向旋转180°后的△A 2B 2C 2．10、（2010•）△ABC 在平面直角坐标系中的位置如下图，将△ABC 沿Y 轴翻折得到△A 1B 1C 1，再将△A 1B 1C 1绕点O 旋转180°得到△A 2B 2C 2．请依次画出△A 1B 1C 1和△A 2B 2C 2． 13、（2010•）在小正方形组成的15×15的网络中，四边形ABCD 和四边形A ′B ′C ′D ′的位置如下图．（1）现把四边形ABCD 绕D 点按顺时针方向旋转90°，画出相应的图形A 1B 1C 1D 1， （2）若四边形ABCD 平移后，与四边形A ′B ′C ′D ′成轴对称，写出满足要求的一种平移方法，并画出平移后的图形A 2B 2C 2D 2．15、（2009•）在建立平面直角坐标系的方格纸中，每个小方格都是边长为1的小正方形，△ABC的顶点均在格点上，点P的坐标为（﹣1，0），请按要求画图与作答．（1）把△ABC绕点P旋转180°得△A′B′C′．（2）把△ABC向右平移7个单位得△A″B″C″．（3）△A′B′C′与△A″B″C″是否成中心对称，若是，找出对称中心P′，并写出其坐标．16、（2009•）如图，已知△ABC的三个顶点的坐标分别为A（﹣2，3）、B（﹣6，0）、C （﹣1，0）．（1）请直接写出点A关于Y轴对称的点的坐标；（2）将△ABC绕坐标原点O逆时针旋转90度．画出图形，直接写出点B的对应点的坐标；（3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．17、（2009•）如下图，每个小方格都是边长为1的正方形，以O点为坐标原点建立平面直角坐标系．（1）画出四边形OABC关于Y轴对称的四边形OA1B1C1，并写出点B1的坐标是_________；（2）画出四边形OABC绕点O顺时针方向旋转90°后得到的四边形OA2B2C2，并求出点C旋转到点C2经过的路径的长度．18、（2009•）如下图的正方形网格中，△ABC 的顶点均在格点上，在所给直角坐标系中解答以下问题：（1）分别写出点A 、B 两点的坐标；（2）作出△ABC 关于坐标原点成中心对称的△A 1B 1C 1；（3）作出点C 关于是X 轴的对称点P ．若点P 向右平移X 个单位长度后落在△A 1B 1C 1的部，请直接写出X 的取值围． 19、（2009•）如图，在每个小正方形的边长均为1个单位长度的方格纸中，有一个△ABC 和一点O ，△ABC 的顶点和点O 均与小正方形的顶点重合．（1）在方格纸中，将△ABC 向下平移5个单位长度得到△A 1B 1C 1，请画出△A 1B 1C 1； （2）在方格纸中，将△ABC 绕点O 旋转180°得到△A 2B 2C 2，请画出△A 2B 2C 2． 20、（2009•）如图，在下面的方格图中，将△ABC 先向右平移四个单位得到△A 1B 1C 1，再将△A 1B 1C 1绕点A 1逆时针旋转90°得到△A 1B 2C 2，请依次作出△A 1B 1C 1和△A 1B 2C 2．21、（2008•永春县）在边长为1的方格纸中建立直角坐标系XOY，O、A、B三点均为格点．（1）直接写出线段OB的长；（2）将△OAB绕点O沿逆时针方向旋转90°得到△OA′B′．请你画出△OA′B′，并求在旋转过程中，点B所经过的路径的长度．22、（2008•）如图，△AOB中，顶点A，B，O均在格点上，画出△AOB绕点O旋转180°后的三角形．（不要求写做法，证明，但要注明结果）23、（2008•）如图，菱形ABCD（图1）与菱形EFGH（图2）的形状、大小完全相同．（1）请从以下序号中选择正确选项的序号填写；①点E，F，G，H；②点G，F，E，H；③点E，H，G，F；④点G，H，E，F．如果图1经过一次平移后得到图2，那么点A，B，C，D对应点分别是_________；如果图1经过一次轴对称后得到图2，那么点A，B，C，D对应点分别是_________；如果图1经过一次旋转后得到图2，那么点A，B，C，D对应点分别是_________；（2）①图1，图2关于点O成中心对称，请画出对称中心（保留画图痕迹，不写画法）；②写出两个图形成中心对称的一条性质：_________．（可以结合所画图形表达）．24、（2008•眉山）如图，方格纸中△ABC的三个顶点均在格点上，将△ABC向右平移5格得到△A1B1C1，再将△A1B1C1绕点A1逆时针旋转180°，得到△A1B2C2．（1）在方格纸中画出△A1B1C1和△A1B2C2；（2）设B点坐标为（﹣3，﹣2），B2点坐标为（4，2），△ABC与△A1B2C2是否成中心对称？若成中心对称，请画出对称中心，并写出对称中心的坐标；若不成中心对称，请说明理由．25、（2008•）如下图，在网格中建立了平面直角坐标系，每个小正方形的边长均为1个单位长度，将四边形ABCD绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1．（1）直接写出D1点的坐标；（2）将四边形A1B1C1D1平移，得到四边形A2B2C2D2，若D2（4，5），画出平移后的图形．（友情提示：画图时请不要涂错阴影的位置哦！）26、（2008•来宾）如图，已知△ABC关于直线MN的对称图形是△A1B1C1，将△A1B1C1绕点A1逆时针旋转90°得到△A1B2C2．请在图中分别画出△A1B1C1和△A1B2C2，并正确标出对应顶点的字母．（不要求写出画法）27、（2008•）在如下图出方格纸中，每个小正方形的边长都为1．（1）画出将铅笔图形ABCDE向上平移9格得到的铅笔图形A1B1C1D1E1；（2）将铅笔图形A1B1C1D1E1，绕点A1，逆时针旋转90°，画出转后的铅笔图形A1B2C2D2E2．28、（2008•）如图，在平面直角坐标系中，△ABC和△A1B1C1关于点E成中心对称．（1）画出对称中心E，并写出点E、A、C的坐标；（2）P（a，b）是△ABC的边AC上一点，△ABC经平移后点P的对应点为P2（a+6，b+2），请画出上述平移后的△A2B2C2，并写出点A2、C2的坐标；（3）判断△A2B2C2和△A1B1C1的位置关系．（直接写出结果）29、（2008•）△ABC在平面直角坐标系中的位置如下图．（1）将△ABC向右平移6个单位得到△A1B1C1，请画出△A1B1C1；并写出点C1的坐标；（2）将△ABC绕原点O旋转180°得到△A2B2C2，请画出△A2B2C2．30、（2008•）已知：如图，在8×12的矩形网格中，每个小正方形的边长都为1，四边形ABCD的顶点都在格点上．（1）在所给网格中按以下要求画图：①在网格中建立平面直角坐标系（坐标原点为O），使四边形ABCD各个顶点的坐标分别为A（﹣5，0）、B（﹣4，0）、C（﹣1，3）、D（﹣5，1）；②将四边形ABCD沿坐标横轴翻折180°，得到四边形A′B′C′D′，再把四边形A′B′C′D′绕原点O旋转180°，得到四边形A″B″C″D″；（2）写出点C″、D″的坐标；（3）请判断四边形A″B″C″D″与四边形ABCD成何种对称？若成中心对称，请写出对称中心；若成轴对称，请写出对称轴．答案与评分标准一、解答题（共30小题）1、（2010•）如图，在边长为1的小正方形组成的网格中，△AOB的三个顶点均在格点上，点A、B 的坐标分别为A（﹣2，3）、B（﹣3，1）．（1）画出坐标轴，画出△AOB绕点O顺时针旋转90°后的△A1OB1；（2）点A1的坐标为（3，2）；（3）四边形AOA1B1的面积为8．考点：作图-旋转变换。

旋转练习题集锦（含答案）一、作图题1、如图，在每个小正方形的边长均为1个单位长度的方格纸中，有一个和一点O，的顶点和点O均与小正方形的顶点重合．（1）在方格纸中，将△ABC向下平移5个单位长度得到，请画出；（2）在方格纸中，将△ABC绕点O旋转180°得到，请画出。

二、简答题2、如图，已知的三个顶点的坐标分别为、、．（1）请直接写出点关于轴对称的点的坐标；（2）将绕坐标原点逆时针旋转90°．画出图形，直接写出点的对应点的坐标；（3）请直接写出：以为顶点的平行四边形的第四个顶点的坐标．三、选择题3、如图所示，在平面直角坐标系中，点A、B的坐标分别为（2，0）和（2，0）.月牙①绕点B顺时针旋转900得到月牙②，则点A的对应点A’的坐标为【】（A）（2，2）（B）（2，4）(C)（4，2） (D)（1，2）4、将图按顺时针方向旋转90°后得到的是( )5、在方格纸（每个小方格都是边长为1个单位长度的正方形）中，我们把每个小正方形的顶点称为格点，以格点为顶点的图形称为格点图形．如上图中的△ABC称为格点△ABC．现将图中△ABC绕点A顺时针旋转，并将其边长扩大为原来的2倍，则变形后点B的对应点所在的位置是（）A．甲 B．乙C．丙 D．丁6、下图是一个旋转对称图形，以O为旋转中心，以下列哪一个角为旋转角旋转，能使旋转后的图形与原图形重合（）A．60° B．90° C．120°D．180°7、在下图右侧的四个三角形中，不能由△ABC经过旋转或平移得到的是 ( )8、下面四个图案中，是旋转对称图形的是（）Ａ．Ｂ．Ｃ．Ｄ．9、下列运动是属于旋转的是( )A．电梯的上下运动 B．火车的运动C．钟表中分针的运动 D．升国旗时，国旗的徐徐运动10、如图所示，将其中的图甲变成图乙，可经过的变换是( )A．旋转、平移 B．平移、对称 C．旋转、对称 D．不能确定11、如图，该图形围绕自己的旋转中心，按下列角度旋转后，不能与其自身重合的是（）A．72° B．108° C．144° D．216°12、如图，D是等腰Rt△ABC内一点，BC是斜边，如果将△ABD绕点A逆时针方向旋转到△ACD’的位置，则∠ADD’的度数是( )A．25° B．30° C．35°D．45°13、如图可以看作是一个等腰直角三角形旋转若干次而成的，则每次旋转的度数最小是( )A．90° B．60° C．45°D．30°14、如图，经过平移或旋转不可能将图甲变为图乙的是（）15、下列图形中，既是中心对称图形，又是轴对称图形的是（）A．菱形B．等边三角形 C．等腰三角形D．平行四边形16、如图所示，可由一个“基本图案”旋转l80°而形成的是（）A B CD17、已知，将点A1（6，1）向左平移4个单位到达点A2的位置，再向上平移3个单位到达点A3的位置，△A1A2A3绕点A2逆时针方向旋转900，则旋转湖A3的坐标为（）A．（－2，1） B．（1，1） C．（－1，1） D．（5，1）18、下图是一张边被裁直的白纸，把一边折叠后，BC、BD为折痕，、、B在同一直线上，则∠CBD的度数（）A．不能确定B．大于C．小于 D．等于四、计算题19、将一张透明的平行四边形胶片沿对角线剪开，得到图①中的两张三角形胶片和．将这两张三角形胶片的顶点与顶点重合，把绕点顺时针方向旋转，这时与相交于点．（1）当旋转至如图②位置，点，在同一直线上时，与的数量关系是．（2）当继续旋转至如图③位置时，（1）中的结论还成立吗？请说明理由．（3）在图③中，连接，探索与之间有怎样的位置关系，并证明．20、如图所示，左边方格纸中每个正方形的边长均为a，右边方格纸中每个正方形的边长均为b，将左边方格纸中的图形顺时针旋转90°，并按b:a的比例画在右边方格纸中．21、点B．C．E在同一直线上，点A．D在直线CE的同侧，AB＝AC，EC＝ED，∠BAC＝∠CED，直线AE、BD交于点F。

第2课时旋转作图及变换知识点1.图形旋转的性质是：(1)旋转前后的图形；(2)对应点到旋转中心的距离；(3)对应点与旋转中心所连线段的夹角等于2.简单的旋转作图---旋转作图的步骤（1）确定旋转；（2）找出图形的关键点；（3）将图形的关键点与旋转中心连接起来，然后按旋转方向分别将它们旋转一个角，得到此关键点的对应点；(4)按图形的顺序连接这些对应点，所得到的图形就是旋转后的图形。

一、选择题1．在图形旋转中，下列说法错误的是（）A．在图形上的每一点到旋转中心的距离相等B．图形上每一点移动的角度相同C．图形上可能存在不动的点D．图形上任意两点的连线与其对应两点的连线长度相等2．如图，下面的四个图案中，既包含图形的旋转，又包含图形的轴对称的是（）3.如图所示的图案绕旋转中心旋转后能够与自身重合，那么它的旋转角可能是（）。

A.60°B.90°C.72°D.120°4．如图，摆放有五杂梅花，下列说法错误的是（以中心梅花为初始位置）（• ）A．左上角的梅花只需沿对角线平移即可B．右上角的梅花需先沿对角线平移后，再顺时针旋转45°C．右下角的梅花需先沿对角线平移后，再顺时针旋转180D．左下角的梅花需先沿对角线平移后，再顺时针旋转90°5 △ABC绕着A 点旋转后得到△AB′C′，若∠BAC′=130°，∠BAC=80°，•则旋转角等于（）A．50° B．210° C．50°或210° D．130°二、填空题6．图形的平移、旋转、轴对称中，其相同的性质是_________.7．如图，△ABC和△ADE均是顶角为42°的等腰三角形，BC、DE分别是底边，图中的△ABD绕A旋转42°后得到的图形是________，它们之间的关系是______，•其中BD=_________．8、如图，将△OAB绕点0按逆时针方面旋转至△0A′B′，使点B恰好落在边A′B′上．已知AB=4cm，BB′=lcm，则A′B长是_______cm．9、如图，在平面直角坐标系中，点A的坐标为(1，4)，将线段O A绕点O顺时针旋转90°得到线段OA′，则点A′的坐标是___________. 10．如图，自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F，•∠EAF=45°，在保持∠EAF=45°的前提下，当点E、F分别在边BC、CD上移动时，BE+•DF•与EF的关系是________．11.如图，在直角坐标系中，已知点)0,3(A、)4,0(B，对△OAB 连续作旋转变换，依次得到三角形①、②、③、④…，则三角形⑩的直角顶点的坐标为__________．三、综合提高题12.观察下列图形，它可以看作是什么“基本图形”通过怎样的旋转而得到的？13.如图：若∠AOD=∠BOC=60°,A、O、C三点在同一条线上，△AOB与△COD 是能够重合的图形。

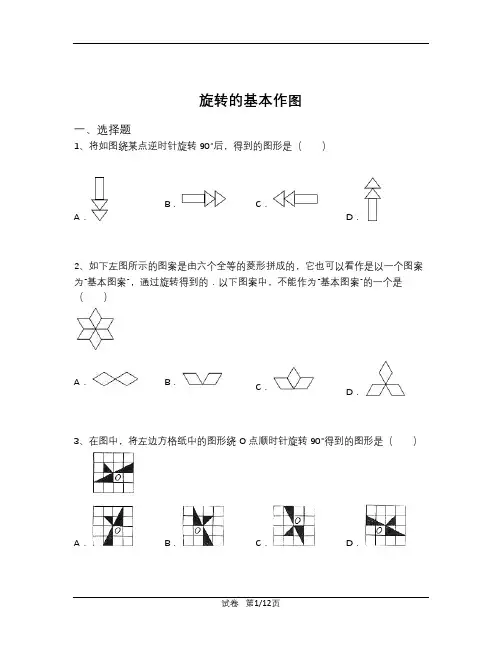
旋转的基本作图一、选择题1、将如图绕某点逆时针旋转90°后，得到的图形是（）A．B．C．D．2、如下左图所示的图案是由六个全等的菱形拼成的，它也可以看作是以一个图案为“基本图案”，通过旋转得到的．以下图案中，不能作为“基本图案”的一个是（）A．B．C．D．3、在图中，将左边方格纸中的图形绕O点顺时针旋转90°得到的图形是（）A．B．C．D．二、解答题4、已知：如图，四边形ABCD及一点P．求作：四边形A′B′C′D′，使得它是由四边形ABCD绕P点顺时针旋转90°得到的．（不写作法保留作图痕迹）5、我们学习过：在平面内，将一个图形绕一个定点沿着某个方向转动一个角度，这样的图形运动叫做旋转，这个定点称为旋转中心，旋转的角度称为旋转角．如图，△ABC经过旋转得到△DEF．试用直尺和圆规作出旋转中心（保留作图痕迹，不写作法）．6、（1）图1，平移方格纸中的图形，使点A平移到点A′处，画出移后的图形．（2）在图2方格纸中画出三角形绕O点逆时针旋转90°后的图形．7、实验操作（1）如图1，在平面直角坐标系xOy中，△ABC的顶点的横、纵坐标都是整数，若将△ABC以点P（1，-1）为旋转中心，按顺时针方向旋转90°得到△DEF，请在坐标系中画出点P及△DEF；（2）如图2，在菱形网格图（最小的菱形的边长为1，且有一个内角为60°）中有一个等边△ABC，它的顶点A，B，C都落在格点上，若将△ABC以点P为旋转中心，按顺时针方向旋转60°得到△A′B′C′，请在菱形网格图中画出△A′B′C′．其中，点A旋转到点A′所经过的路线长为 __________ ．8、如图，△ABC中，∠C=90°，将△ABC绕点A旋转得到△AB1C1，点C的对应点C1恰好落在AB边上．（1）作图：作出△AB1C1（保留作图痕迹，不要求写作法）；（2）已知AC=5，BC=12，求BB1的长．9、如图，已知边长为a的正方形ABCD．求作该正方形绕点A逆时针旋转30°后的正方形AB1C1D1．（说明：请用无刻度的直尺和圆规作图，并保留作图痕迹）10、如图1，正方形ABCD是一个6×6网格电子屏的示意图，其中每个小正方形的边长为1．位于AD中点处的光点P按图2的程序移动．（1）请在图1中画出光点P经过的路径；（2）求光点P经过的路径总长（结果保留π）．11、画△ABC绕O点顺时针方向旋转90°后得到△A′B′C′．12、如图，在10×10的小正方形网格中，△ABC的顶点A、B、C在网格点上，P1、P2、P3、P4是其中一个小正方形的四个格点，将△ABC绕A点逆时针旋转90°，再向下平移2个单位，得到△A′B′C′；将△ABC按一定的规律顺次旋转，第一次将△ABC绕点P1逆时针旋转90°得到△A1B1C1；第二次将△A1B1C1绕点P2逆时针旋转90°得到△A2B2C2；第三次将△A2B2C2绕点P3逆时针旋转90°得到△A3B3C3，依次按旋转中心为P1、P2、P3、P4、P1、P2…旋转下去．（1）在网格中画出△A′B′C′和△A2B2C2；（2）△ABC至少旋转第__________次后所得的三角形刚好与△A′B′C′重合．13、如图所示，左边方格纸中每个正方形的边长均为a，右边方格纸中每个正方形的边长均为b，将左边方格纸中的图形顺时针旋转90°，并按b：a的比例画在右边方格纸中．14、请按下面要求画图（1）请在图1中画出一个直角梯形MNPQ，使它与梯形ANMB构成一个等腰梯形；（2）在图2中，将直角梯形ABMN绕点M按逆时针旋转180°，画出旋转后的图形．15、分析图①、②、④中阴影部分的分布规律，按此规律在图③中画出其中的阴影部分．旋转的基本作图的答案和解析一、选择题1、答案：C试题分析：抓住几个关键图形逆时针旋转90°后的位置，结合选项进行判断即可．试题解析：绕某点逆时针旋转90°后，得到的图形是．故选C．2、答案：B试题分析：认真观察旋转得到的图案，找到旋转中心，即可判断．试题解析：A、顺时针，连续旋转60度，三次即可得到．B、不能作为“基本图案”．C、旋转180度，即可得到．D、旋转60度即可．故选B．3、答案：B试题分析：根据旋转的性质，找出图中三角形的关键处（旋转中心）按顺时针方向旋转90°后的形状即可选择答案．试题解析：根据旋转的性质可知，绕O点顺时针旋转90°得到的图形是．故选B．二、解答题4、答案：试题分析：利用旋转的性质分别得出对应点位置进而得出答案．试题解析：如图所示：四边形A′B′C′D′即为所求．5、答案：试题分析：根据旋转的性质，连接对应点AD、BE，再分别作AD、BE的垂直平分线，相交于点O，则点O即为旋转中心．试题解析：如图所示，点O即为△ABC旋转到△DEF的旋转中心．6、答案：试题分析：（1）利用网格特点和平移的性质画图；（2）利用网格特点和旋转的性质画图．试题解析：（1）如图1：（2）如图2：7、答案：试题分析：（1）先做出P点，然后找出点A、B、C绕点P顺时针旋转90°的位置，然后顺次连接即可；（2）找出点A、B、C绕点P顺时针旋转60°的位置，顺次连接A'B'、B'C'、C'A'，然后根据弧长公式求出点A旋转到点A′所经过的路线长．试题解析：（1）（2）所作图形如下：；点A的运动路线==π．故答案为：π．8、答案：试题分析：（1）以点A为圆心，以AC为半径画弧，与AB相交于点C1，再以点A为圆心，以AB为半径画弧，以C1为圆心，以CB为半径画弧，两弧相交于点B1，然后顺次连接即可；（2）利用勾股定理列式求出AB，再求出BC1，再利用勾股定理列式计算即可得解．试题解析：（1）△AB1C1如图所示；（2）由勾股定理得，AB==13，BC1=13-5=8，B1C1=12，所以，BB1==4．9、答案：试题分析：①以点A为圆心，AD长为半径作圆，再以点D为圆心，DA长为半径作弧，与圆的交点为E，连接AE，DE，△ADE就是一个等边三角形．∠EAD=60°；②作∠EAD的角平分线，得到一个30°的角，角平分线与圆的交点为D1；③连接AC，以AC为一边根据②中30度的角作∠CAC1=30°，以点A为圆心，AC长为半径画弧与角的另一边交点为C1；④以AB为一边，作∠BAB1等于已知角30度，与圆的交点为B1．试题解析：所作图形如下：10、答案：试题分析：（1）按图2中的程序旋转一一找到对应点，第一次是绕点A顺时针旋转90°，得到对应点，再绕点B顺时针旋转90°，得到对应点．再绕点C顺时针旋转90°，得到对应点，再绕点D顺时针旋转90°，得到对应点即可．（2）从中可以看出它的路线长是4段弧长，根据弧长公式计算即可．（1）如图；（2）∵，∴点P经过的路径总长为6π．11、答案：试题分析：根据旋转的性质，将A，B，C绕O点顺时针旋转90°，由此即可画出旋转后的图形．试题解析：如图所示：12、答案：试题分析：（1）根据旋转和平移的概念在网格中画出△A′B′C′和△A2B2C2；（2）根据△ABC的旋转规律，把△ABC进行旋转，得到三角形刚好与△A′B′C′重合的旋转次数．试题解析：（1）如图：（2）把点A按照△ABC的旋转规律进行旋转，可以发现旋转第5次后所得的三角形刚好与A′重合，故答案为：5．13、答案：试题分析：将左边方格纸中的图形顺时针旋转90°，并按b：a的比例画在右边方格纸中．因为方格的比例就是b：a，所以只要顺时针旋转90°，在格点上的还让它在格点上，得到的图形就是所求的图形．试题解析：14、答案：试题分析：（1）画出一个直角梯形MNPQ，使它与梯形ANMB构成一个等腰梯形；根据等腰梯形的性质，即可作出图形；（2）将直角梯形ABMN绕点M按逆时针旋转180°，根据旋转的性质，即可作出旋转后的图形．试题解析：（1）如图1：（2）如图2：15、答案：试题分析：由①到②是旋转了90°，由②到④是旋转了180度，即通过两次旋转90度得到，据此即可判断．试题解析：如图。

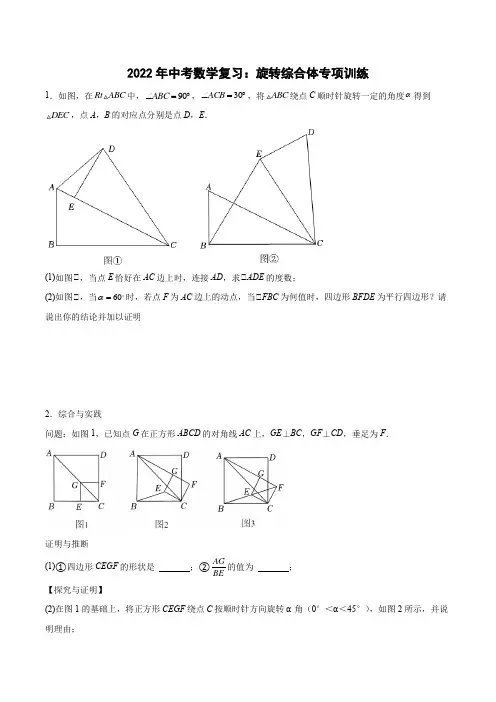
2022年中考数学复习：旋转综合体专项训练1．如图，在Rt ABC 中，90ABC ∠=︒，30ACB ∠=︒，将ABC 绕点C 顺时针旋转一定的角度α得到DEC ，点A ，B 的对应点分别是点D ，E ．(1)如图①，当点E 恰好在AC 边上时，连接AD ，求①ADE 的度数；(2)如图①，当60α=时，若点F 为AC 边上的动点，当①FBC 为何值时，四边形BFDE 为平行四边形？请说出你的结论并加以证明2．综合与实践问题：如图1，已知点G 在正方形ABCD 的对角线AC 上，GE ⊥BC ，GF ⊥CD ，垂足为F ．证明与推断(1)①四边形CEGF 的形状是 ；②AGBE的值为 ； 【探究与证明】(2)在图1的基础上，将正方形CEGF 绕点C 按顺时针方向旋转α角（0°＜α＜45°），如图2所示，并说明理由；【拓展与运用】(3)如图3，在（2）的条件下，正方形CEGF 在旋转过程中，AG 和GE 的位置关系是 ．3．若①ABC ，①ADE 为等腰三角形，AC ＝BC ，AD ＝DE ，将①ADE 绕点A 旋转，连接BE ，F 为BE 中点，连接CF ，DF ．(1)若①ACB ＝①ADE ＝90°，如图1，试探究DF 与CF 的关系并证明； (2)若①ACB ＝60°，①ADE ＝120°，如图2，请直接写出CF 与DF 的关系．4．在平面直角坐标系中，点(0,0)O ，点A ，点)(0),30B m m AOB >∠=︒．以点O 为中心，逆时针旋转OAB ，得到OCD ，点,A B 的对应点分别为,C D ．记旋转角为α．(1)如图①，当点C 落在OB 上时，求点D 的坐标；(2)如图①，当45α=︒时，求点C 的坐标；(3)在（2）的条件下，求点D 的坐标（直接写出结果即可）．5．如图，30HAB ∠=︒，点B 与点C 关于射线AH 对称，连接AC ．D 点为射线AH 上任意一点，连接CD ．将线段CD 绕点C 顺时针旋转60°，得到线段CE ，连接BE ．（1）求证：直线EB 是线段AC 的垂直平分线；（2）点D 是射线AH 上一动点，请你直接写出ADC ∠与ECA ∠之间的数量关系．6．已知如图，等腰△ABC 中，AB=AC ，△BAC=α（α>90︒），F 为BC 中点，D 为BC 延长线上一点，以点A 为中心，将线段AD 逆时针旋转α得到线段AE ，连接CE ，DE ．(1)补全图形并比较△BAD 和△CAE 的大小； (2)用等式表示CE ，CD ，BF 之间的关系，并证明；(3)过F 作AC 的垂线，并延长交DE 于点H ，求EH 和DH 之间的数量关系，并证明．7．一副三角尺（分别含30°，60°，90°和45°，45°，90°）按如图所示摆放，边OB ，OC 在直线l 上，将三角尺ABO 绕点O 以每秒10°的速度顺时针旋转，当边OA 落在直线l 上时停止运动，设三角尺ABO 的运动时间为t 秒．（1）如图，①AOD ＝ °＝ ′； （2）当t ＝5时，①BOD ＝ °； （3）当t ＝ 时，边OD 平分①AOC ；（4）若在三角尺ABO 开始旋转的同时，三角尺DCO 也绕点O 以每秒4°的速度逆时针旋转，当三角尺ABO 停止旋转时，三角尺DCO 也停止旋转．在旋转过程中，是否存在某一时刻使①AOC ＝2①BOD ，若存在，请直接写出的值；若不存在，请说明理由．8．如图，正方形ABCO 的边OA 、OC 在坐标物上，点B 坐标为()3,3．将正方形ABCO 绕点A 顺时针旋转角度()090αα︒<<︒，得到正方形ADEF ，ED 交线段OC 于点G ，ED 的延长线交线段BC 于点P ．连AP 、AG ．（1）求证：AOG①ADG；∠的度数；并判断线段OG、PG、BP之间的数量关系，说明理由；（2）求PAG（3）当12∠=∠时，求直线PE的解析式（可能用到的数据：在Rt中，30°内角对应的直角边等于斜边的一半）．（4）在（3）的条件下，直线PE上是否存在点M，使以M、A、G为顶点的三角形是等腰三角形？若存在，请直接写出M点坐标；若不存在，请说明理由．9．如图，等腰Rt①ABC中，AB＝AC，D为线段BC上的一个动点，E为线段AB上的一个动点，使得CD=．连接DE，以D点为中心，将线段DE顺时针旋转90°得到线段DF，连接线段EF，过点D作射线DR①BC交射线BA于点R，连接DR，RF．（1）依题意补全图形；（2）求证：①BDE①①RDF；（3）若AB＝AC＝2，P为射线BA上一点，连接PF，请写出一个BP的值，使得对于任意的点D，总有①BPF为定值，并证明．10．在①ABC中，AB＝AC，①BAC＝90°，D为平面内的一点．（1）如图1，当点D在边BC上时，BD＝2，且①BAD＝30°，AD＝；（2）如图2，当点D在①ABC的外部，且满足①BDC﹣①ADC＝45°，求证：BD AD；（3）如图3，若AB ＝4，当D 、E 分别为AB 、AC 的中点，把①DAE 绕A 点顺时针旋转，设旋转角为α（0＜α≤180°）直线BD 与CE 的交点为P ，连接P A ，直接出①P AB 面积的最大值 ．11．已知：①ABC 为等边三角形，且AB ＝4，点D 在直线BC 上运动，线段DA 绕着点D 顺时针旋转60°得到线段DE ，连接AE 和BE ，直线AE 交直线BC 于点F ． （1）如图，当点D 在点C 左侧时，求证：CD ＝BE ；（2）若①ABC 的面积等于①ABF 面积的4倍，直接写出线段CD 的长；（3）在（2）的条件下，若点E 关于直线AD 的对称点为点G ，连接DG 交线段AC 于点M ，DE 交线段AB 于点N ，连接MN ，直接写出线段MN 的长．12．已知在①ABC 中，90ACB ∠=︒，AC ＝BC ＝（1）如图1，以点A 为原点，AB 所在直线为x 轴建立平面直角坐标系，直接写出点B ，C 的坐标； （2）如图2，过点C 作①MCN ＝45°交AB 于点M ，N ，且AM =1，求MN 的长度；（3）如图3，过点C 作①MCN ＝45°，当点M ，N 分布在点B 异侧时，线段AM ，BN 和MN 满足怎样的数量关系？并给予证明．13．如图，在①ABC 中，AC ＝ BC ，①ACB ＝ 90°，D 是线段AC 延长线上一点，连接BD ，过点A 作AE ①BD 于E ．（1）求证：①CAE ＝①CBD ；（2）将射线AE 绕点A 顺时针旋转45°后，所得的射线与线段BD 的延长线交于点F ，连接CE ． ①依题意补全图形；①用等式表示线段EF ，CE ，BE 之间的数量关系，并证明．14．把两个等腰直角ABC 和ADE 按如图1所示的位置摆放，将ADE 绕点A 按逆时针方向旋转，如图2，连接BD ，EC ，设旋转角为α（0360α︒<<︒）．（1）如图1，BD 与EC 的数量关系是___________，BD 与EC 的位置关系是___________；（2）如图2，（1）中BD 和EC 的数量关系和位置关系是否仍然成立，若成立，请证明；若不成立请说明理由．（3）如图3，当点D 在线段BE 上时，BEC ∠=___________． （4）当旋转角α=__________时，ABD △的面积最大．15．如图，在Rt ①ABC 中，BC ＝4，AC ＝2，①ACB ＝90°，矩形BDEF 的边BF ＝1，BD ＝2，矩形BDEF 可以绕点B 在平面内旋转，连接AE 、BE 、CD ． （1）证明：①ABE ①①CBD ；（2）当A 、E 、F 三点共线时，求CD 的长；（3）设AE 的中点为M ，连接FM ，直接写出FM 的最大值．16．在平面直角坐标系中，四边形AOBC 是矩形，点A 的坐标为()5,0，点B 的坐标为()0,3，以点A 为中心，顺时针旋转矩形AOBC ，得到矩形ADEF ，点O ，B ，C 的对应点分别为D ，E ，F ．（1）如图①，当点D 落在BC 边上时，求点D 的坐标；（2）如图①，当点D 落在线段BE 上时，连接AB ，AD 与BC 交于点H ． ①求证：ADB AOB ≅△△； ①求点H 的坐标．（3）点K 为矩形AOBC 对角线的交点，S 为KDE 得面积，直接写出S 的取值范围．17．如图，P 是正三角形ABC 内的一点，且6,8,10PA PB PC ===，若将PAC △绕点A 顺时针旋转后得到P AB '△，（1）求旋转角的度数；（2）求点P 与点P '之间的距离； （3）求APB ∠的度数．18．如图在平面直角坐标系中，点O 为坐标原点，直线y 34=-x +b 分别交x 轴，y 轴于点A 、B ，OA ＝4，①OBA 的外角平分线交x 轴于点D ．（1）求点D 的坐标；（2）点P 是线段BD 上一点（不与B 、D 重合），过点P 作PC ①BD 交x 轴于点C ，设点P 的横坐标为t ，△BCD 的面积为S ，求S 与t 之间的函数解析式（不要求写出自变量t 的取值范围）；（3）在（2）的条件下，PC 的延长线交y 轴于点E ，当PC ＝PB 时，将射线EP 绕点E 旋转45°交直线AB 于点F ，求F 点坐标．19．如图，在菱形ABCD 中，60ABC ∠=︒，E 为对角线AC 上一点，将线段DE 绕点D 逆时针旋转60︒，点E 的对应点为F ，连接BE ，AF ，CF ．（1）求证：B ，C ，F 三点共线；（2）若点G 为BE 的中点，连接AG ，求证：2AF AG =．20．如图，在四边形ABCD中，BC=CD，△BCD=α°，△ABC+△ADC=180°，AC、BD交于点E．将△CBA 绕点C顺时针旋转α°得到△CDF（点B、A的对应点分别为点D、F）．（1）画出旋转之后的图形（不要求写画法，保留画图痕迹）；（2）求证：△CAB=△CAD；（3）若△ABD=90°，AB=3，BD=4，△BCE的面积为1S，△CDE的面积为2S，求1S:2S的值．参考答案：1．解：①将ABC绕点C顺时针旋转一定的角度α得到①DEC，E点在AC上，①CA=CD，①ECD=①BCA=30︒，(180︒−30︒)=75︒，①①CAD=①CDA=12又①①DEC=①ABC=90︒，①①ADE=90°-75︒=15︒；(2)①FBC=30︒时，四边形BFDE为平行四边形，①①FBC=①ACB=30︒，①①ABF=①A=60︒，①BF=CF=AF，①ABF是等边三角形，①BF=AB，①将ABC绕点C顺时针旋转60︒得到DEC，①DE=AB，BCE是等边三角形，①DEC=①ABC=90︒，①①CBE=①BEC=60︒，①①EBF=①EBC-①FBC=30︒，①①DEB+①EBF=180︒，①DE=BF，//DE BF，①四边形BFDE为平行四边形．2．①正方形；．理由：如图1中，∵四边形ABCD 是正方形，∴∠BCD ＝90°，∠BCA ＝45°，∵GE ⊥BC 、GF ⊥CD ，∴∠CEG ＝∠CFG ＝∠ECF ＝90°，∴四边形CEGF 是矩形，∠CGE ＝∠ECG ＝45°，∴EG ＝EC ，∴四边形CEGF 是正方形，∵AC BC ,，∴AG ＝AC ﹣CGBC ﹣EC ，∴AG BE(2)结论：AG ，理由：如图2中，连接CC ，∵四边形ABCD 是正方形，∴∠ABC ＝90°，AB ＝BC ，∴△ABC 为等腰直角三角形，∴AC BC由①得四边形GECF 是正方形，∴∠GEC ＝∠ECF ＝90°，GE ＝EC ，∴△EGC 为等腰直角三角形．∴CG CE∴AC CG BC EC=∴△ACG ∽△BCE ，∴AG CG BE EC∴线段AG 与BE 之间的数量关系为AG ；(3)如图3中，连接CG ，∵∠CEF ＝45°，点B 、E ，∴∠BEC ＝135°．∵△ACG ∽△BCE ，∴∠AGC ＝∠BEC ＝135°．∴∠AGF ＝∠AGC +∠CGF ＝135°+45°＝180°，∴点A ，G ，F 三点共线，∴∠AGE ＝∠AGF ﹣∠EGF ＝180°﹣90°＝90°，∴AG ⊥GE ，故答案为：AG ⊥GE ．3．(1)DF =CF 且DF ①CF ；延长CF 至点M ，使CF =FM ，连接ME ，MD ，CD ，延长DE 交CB 延长线于点N ，如图1，①BF=EF，CF=FM，①BFC=①EFM，①①BFC①①EFM（SAS），①EM=BC=AC，①FME=①FCB，①BC①EM，①①N=①MEN，在四边形ACND中，①ACB=①ADE=90°，①①N+①CAD=360°-（①ACB+①ADE）=180°，又①①MEN+①MED=180°，①①MED=①CAD，又AD=DE，EM=AC，①①MED①①CAD（SAS），①DM=DC，①MDE=①CDA，①①MDC=①NDC+①MDE=①NDC+①CDA=①ADE=90°，①①DCM为等腰直角三角形，①点F是CM中点，CM=CF，DF①CF；①DF=12(2)DF①CF且CF；延长CF至点M，使CF=FM，连接ME，MD，CD，延长ED交BC延长线于点N，如图2，①BF=EF，CF=FM，①BFC=①EFM，①①BFC①①EFM（SAS），①EM =BC =AC ，①FME =①FCB ，①BC //EM ，①①N =①NER ，①①ACB =60°，①①ACN =120°，①①ADE =120°，①①ADN =60°，①①N +①CAD =360°-（①ACN +①ADN ）=180°，①①DER +①DEM =180°，①①DEM =①CAD ，又 AD =DE ，EM =AC ，①①MED ①①CAD （SAS ），①DM =DC ，①MDE =①CDA ，①①DCM 为等腰三角形，①①CDM =①ADE =120°，①F 是CM 的中点，①DF ①CF①60CDF ∠=︒①30DCF ∠=︒①CD =2DE由勾股定理得，222CE DE CD +=①2224CE DE DE +=解得，CF （负值舍去）①DF ①CF 且CF ．4．(1)如图，过点D 作DE OA ⊥，垂足为E ．① 0A ，B m ）0m （＞），① AB OA ⊥，OA =AB m =．① 30AOB ∠=︒，① 22OB AB m ==．在Rt OAB 中，由222OA AB OB +=，得2234m m +=．解得1m =．① 1AB =，2OB =．① OCD 是由OAB 旋转得到的，① 2OD OB ==，30DOC AOB ∠=∠=︒．① 60DOE DOC BOA ∠=∠+∠=︒．① 9030ODE DOE ∠=︒-∠=︒．① 112OE OD ==． 在Rt OED 中，DE =① 点D 的坐标为（．(2)如图，过点C 作CT OA ⊥，垂足为T ．由已知，得45COT ∠=︒．① 9045OCT COT ∠=︒-∠=︒．① OT CT=．① OCD是由OAB旋转得到的，① OC OA==在Rt OTC△中，由222T TO C OC+=，得OT CT=① 点C的坐标为．(3)如图①中，过点D作DJ①OA于点J，在DJ上取一点K，使得DK=OK，设OJ=m．①①DOC=30°，①COT=45°，①①DOJ=75°，①①ODJ=90°-75°=15°，①KD=KO，①①KDO=①KOD=15°，①①OKJ=①KDO+①KOD=30°，①OK=DK=2m，KJ，①OD2=OJ2+DJ2，①22=m2+（2m）2，解得m=，①OJ DJ①D⎫⎪⎪⎝⎭．5．（1）证明：连接AE，DB，CB①点B 与点C 关于射线AH 对称，30HAB ∠=︒ ①CD BD =，AC AB =①30HAB HAC ∠∠==︒①260CAB HAC ∠∠==︒①ABC 为等边三角形，60ACB ∠=︒ ①60DCE ∠=︒①DCE ACD ACB ACD ∠∠∠∠-=- ECA DCB ∠=∠①在ECA △和DCB 中，EC DC ECA DCB AC BC =⎧⎪∠=∠⎨⎪=⎩①()ECA DCB SAS ≅△△①BD EA =①DC BD EC ==，①AE EC =又AB BC =①EB 垂直平分AC（2）分两种情况来讨论：第一种情况，如图，当点D 在ABE △内部时：①点B 与点C 关于射线AH 对称，①90CFA ∠=︒①90ADC CFA DCB DCB ∠=∠+∠=︒+∠ ①ECA DCB ∠=∠①90ADC ECA ∠=︒+∠第二种情况，如图，当点D 在ABC 外部时： ①点B 与点C 关于射线AH 对称，①90CFA ∠=︒①90ADC CFA DCB DCB ∠=∠-∠=︒-∠ ①ECA DCB ∠=∠①90ADC ECA ∠=︒-∠6．如图，即为补全的图形，根据题意可知BAC DAE α∠=∠=，①BAC CAD DAE CAD ∠+∠=∠+∠，即BAD CAE ∠=∠．(2)由旋转可知AD AE =，①在BAD 和CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，①()BAD CAE SAS ≅，①BD CE =．①BD BC CD =+，①CE BC CD =+．①点F 为BC 中点，①2BC BF =，①2CE BF CD =+，即2CE CD BF -=．(3)如图，连接AF ，作AN DE ⊥，①AB=AC ，F 为BC 中点，①90AFD ∠=︒，12FAB FAC α∠=∠=． 根据作图可知90AND ∠=︒，①180AFD AND ∠+∠=︒，①A 、F 、D 、N 四点共圆，①AFN ADN ∠=∠．①AD AE =，AN DE ⊥，①EN DN =，11(180)9022AFN ADN DAE α∠=∠=︒-∠=︒-． ①11909022AFN FAC αα∠+∠=︒-+=︒． ①90AFH FAC ∠+∠=︒，且点H 在线段DE 上，①点H 与点N 重合，①EH DH =．7．（1）①180AOD AOB COD ∠=︒-∠-∠，3045AOB COD ∠=︒∠=︒，，①10510560=6300AOD '∠=︒=⨯．故答案为：105，6300；（2）当5t =时，即三角尺ABO 绕点O 顺时针旋转了51050⨯︒=︒，如图，ABO 即为旋转后的图形．由旋转可知50BOM ∠=︒，①180180455085BOD COD BOM ∠=︒-∠-∠=︒-︒-︒=︒，故答案为85；（3）当三角尺绕点O 顺时针旋转到如图所示的ABO 的位置时，边OD 平分①AOC ．①224590AOC COD ∠=∠=⨯︒=︒，①90AOM ∠=︒①90903060BOM AOB ∠=︒-∠=︒-︒=︒， ①60610t ==； 故答案为：6；（4）①当边OA 落在直线l 上时停止运动时， ①180150=1510t -≤． 当OA 和OC 重合时，即有10418030t t +=︒-︒， 解得：757t =． ①当757t ≤时，1801030415014AOC t t t ∠=︒--︒-=︒-， 当757t >时，1030418014150AOC t t t ∠=+︒+-︒=-︒． 当OB 和OD 重合时，即有10418045t t +=︒-︒， 解得：13514t =①当13514t ≤时，1801045413514BOD t t t ∠=︒--︒-=︒-， 当13514t >时，1045418014225BOD t t t ∠=+︒+-︒=-︒． ①可根据2AOC BOD ∠=∠分类讨论，①当13514t ≤时，有15014=2(13514)t t ︒-︒-， 解得：607t =，符合题意； ①当13575147t <≤时，即有150142(14225)t t ︒-=-︒ 解得：1007t =，符合题意； ①当757t >时，即有141502(14225)t t -︒=-︒解得：150157t =>，不符合题意舍； 综上，可知当607t =或1007t =时，2AOC BOD ∠=∠． 8．（1）证明：在Rt△AOG 和Rt△ADG 中，AO AD AG AG=⎧⎨=⎩ ①AOG ①ADG （HL ）．（2）在Rt ①ADP 和Rt ①ABP 中，AD AB AP AP=⎧⎨=⎩ ΔΔADP ABP ∴≅（HL ）， 则DAP BAP ∠=∠；ΔΔAOG ADG ≅，1DAG ∴∠=∠；又190DAG DAP BAP ∠+∠+∠+∠=︒，2290DAG DAP ∴∠+∠=︒，45DAG DAP ∴∠+∠=︒，PAG DAG DAP ∠=∠+∠，45∴∠=︒PAG ；ΔΔAOG ADG ≅，DG OG ∴=，ΔΔADP ABP ≅，DP BP ∴=，PG DG DP OG BP ∴=+=+．（3）解：ΔΔAOG ADG ≅，AGO AGD ∴∠=∠，又190AGO ∠+∠=︒，290PGC ∠+∠=︒，12∠=∠，AGO PGC ∴∠=∠，又AGO AGD ∠=∠，AGO AGD PGC ∴∠=∠=∠，又180AGO AGD PGC ∠+∠+∠=︒，180360AGO AGD PGC ∴∠=∠=∠=︒÷=︒，12906030∴∠=∠=︒-︒=︒；∴在Rt ΔAOG 中，2,3AG OG OA ==，222AG OG OA =+∴222(2)3OG OG =+ 解得OGG ∴点坐标为0)，3CG =在Rt ΔPCG 中，2PG CG =，222PG CG PC =+∴222(2)CG CG PC =+， ∴3PC =，P ∴点坐标为：(3，3)，设直线PE 的解析式为：y kx b =+，则033b k b +=+=⎪⎩，解得3k b ⎧=⎪⎨=-⎪⎩∴直线PE 的解析式为3y =-．（4）①如图1，当点M 在x 轴的负半轴上时，AG MG =，点A 坐标为(0,3)，∴点M 坐标为(0,3)-．①如图2，当点M 在EP 的延长线上时，由（3），可得60AGO PGC ∠=∠=︒，EP ∴与AB 的交点M ，满足AG MG =，A 点的横坐标是0，GM ∴的横坐标是3，∴点M 坐标为3)．综上，可得点M 坐标为(0,3)-或3)．9．（1）如图，（2）DR ①BC90RDB ∴∠=︒将线段DE 顺时针旋转90°得到线段DF ，90,EDF ED FD ∴∠=︒=BDR EDF ∴∠=∠即BDE EDR EDR RDF ∠+∠=∠+∠BDE RDF ∴∠=∠ ABC 是等腰直角三角形90BDR ∠=︒45BRD ∴∠=︒BRD ∴是等腰直角三角形BD DR ∴=∴①BDE ①①RDF ；（2）如图，当24PB AB ==时，使得对于任意的点D ，总有①BPF 为定值，证明如下，ABC 是等腰直角三角形，2AB AC ==BC ∴=DC =设DE a =，则CD =，①BDE ①①RDF ,DR BD ∴==，FR BR a == ABC 是等腰直角三角形，45EBD ∴∠=︒DR BC ⊥45BRD ∴∠=︒BDR ∴是等腰直角三角形，42BR a ∴==-()4422PR BP BR a a ∴=-=--=①BDE ①①RDF ,45FRD EBD ∴∠=∠=︒90BRF BRD DRF ∴∠=∠+∠=︒1tan 22RF a BPF RP a ∴∠=== BPF ∴∠为定值10．证明：（1）如图1，将①ABD 沿AB 折叠，得到①ABE ，连接DE ，①AB ＝AC ，①BAC ＝90°，①①ABC ＝45°，①将①ABD 沿AB 折叠，得到①ABE ，①①ABD ①①ABE ，①AE ＝AD ，BE ＝BD ，①ABE ＝①ABD ＝45°，①BAD ＝①BAE ＝30°，①①DBE ＝90°，①DAE ＝60°，且AD ＝AE ，BE ＝BD ，①①ADE 是等边三角形，DE =，①AD ＝DE =故答案为：（2）如图2，过点A 作AE ①AD ，且AE ＝AD ，连接DE ，①AE ①AD ，①①DAE ＝①BAC ＝90°，①①BAE ＝①DAC ，且AD ＝AE ，AB ＝AC ，①①BAE ①①CAD （SAS ）①①ACD＝①ABE，①①ACD+①DCB+①ABC＝90°，①①DCB+①ABC+①ABE＝90°，①①BOC＝90°，①AE＝AD，AE①AD，①DE=，①ADE＝45°，①①BDC﹣①ADC＝45°，①①BDC＝①ADC+45°＝①EDC，且DO＝DO，①DOB＝①DOE＝90°，①①DOB①①DOE（ASA）①BD＝DE，①BD=；（3）如图3，连接PC交AB于G点①①DAE绕A点旋转①AD=AE，AB=AC,①①DAE=①BAC=90°①①DAB=①EAC①①DAB①①EAC①①DBA=①ECA①①PGB=①AGC①①BPC=①GAC=90°①①BPC为直角三角形①点P在以BC中点M为圆心，BM为半径的圆上，连接PM交AB所在直线于点N，当PM①AB时，点P到直线AB的距离最大，①①BAC=90°①A 、P 、B 、C 四点共圆①PM ①AB ，①N 是AB 的中点①M 是BC 的中点①MN =122AC = ①AB ＝AC ＝4，①CB =22442，①BM =PM =12BC =，①PN ＝2 ，①点P 到AB 所在直线的距离的最大值为：PN ＝2 ． ①①P AB的面积最大值为12AB ×PN ＝4． 11．（1）证明：ABC 是等边三角形60,BAC AB AC ∴∠=︒=线段DA 绕着点D 顺时针旋转60°得到线段DE ， 60,DAE DA DE ∴∠=︒=ADE ∴是等边三角形DAC DAE CAE BAC CAE EAB ∴∠=∠-∠=∠-∠=∠ 即DAC EAB ∠=∠∴ADC AEB △≌△∴CD BE =（2）ABC 是等边三角形，AB ＝4，则60BAC ∠=︒过点A 作AM BC ⊥，则1302BAH BAC ∠=∠=︒ Rt ABH 中，122BH AB ==AH ∴=142ABC S ∴=⨯⨯△①ABC 的面积等于①ABF 面积的4倍ABF S ∴=△11sin 60422ABF S BF AB =⋅⨯︒=⨯=△ 1BF ∴= ①当F 点在B 点的左侧时，如图，60ACB ABC ∠=∠=︒120ACD ∴∠=︒ADC AEB △≌△ADC AEB ∴∠=∠，BE DC =60ABC ∠=︒60EBF ABE ABC ∴∠=∠-∠=︒60FBE FCA ∴∠=∠=︒又AFC EFB ∠=∠AFC EFB ∴∽FB BE FC AC∴= 4,1AC BC AB BF ====413FC ∴=-=14433FB AC BE FC ⋅⨯∴=== 43CD EB ∴==①当F 点在B 点的右侧时，如图，ADC AEB △≌△60ACD EBA ∴∠=∠=︒60ABC ∠=︒18060EBF ABC ABE ∴∠=︒-∠-∠=︒BE AC ∴∥FEB FAC ∴∽FB BE FC AC∴= 1,4,145FB AC FC BC BF ===+=+=45FB AC BE FC ⨯∴== 45CD EB ∴==综上所述CD 的长为43或45（3）如图，点E 关于直线AD 的对称点为点G ，ADE 是等边三角形60ADE ADG ∴∠=∠=︒，AE AD =AEN ADM ∴∠=∠60=︒60,60MAD DAB CAB EAB DAB DAE ∠+∠=∠=︒∠+∠=∠=︒MAD NAE ∴∠=∠MAD NAE ∴=AM AN ∴=60MAN ∠=︒AMN ∴是等边三角形MN AN ∴=由（2）可得45BE =，FEB FAC ∽ 445525EF BF BF AF FC BC BF ∴====+过点A 作AH BC ⊥，则AH =,2CH HB ==，3HF HB BF =+=AF ∴=425EF AF ∴==AE AF EF ∴=-==60,ABE AEN EAB NAE ∠=∠=︒∠=∠∴BEA ENA ∽BE BA EN EA∴= 则BE EA EN BA ⨯=60,ADN ABE AND ENB ∠=∠=︒∠=∠ADN EBN ∴∽AD AN EB EN∴= 即AN EB EN AD ⨯= BE EA AN EB BA AD ⨯⨯∴= EA AD AN AB⨯∴=AE AD =,4AB =2926142500AN ⎝⎭∴== 即92612500MN =12． 解：（1）如图1，过点C 作CD ①x 轴于D ，①在①ABC 中，90ACB ∠=︒，AC ＝BC＝①4AB = ，①点B （4，0），①CD ①AB ，①AD ＝CD ＝12AB ＝12×4＝2，①点C 的坐标为（2，2）；（2）如图，把①ACM 绕点C 逆时针旋转90°得到①BCM ′，连接M ′N ，①90ACB ∠=︒，AC ＝BC ，①①ABC 是等腰直角三角形，①①CAB ＝①CBA ＝45°，由旋转的性质得，45AM BM CM CM CAM CBM ACM BCM '''==∠=∠=︒∠=∠'、、，，①454590M BN ABC CBN ∠'=∠+∠'=︒+︒=︒ ，①①MCN ＝45°，①90904545M CN BCN BCM BCN ACM MCN ∠'=∠+∠'=∠+∠=︒-∠=︒-︒=︒ ， ①MCN M CN ∠=∠' ，在①MCN 和①M ′CN 中，①CM CM MCN M CN CN CN ''=⎧⎪∠=∠⎨⎪=⎩，①MCN M CN SAS '≌（）， ①MN M N =' ，在Rt M NB ' 中，222BM BN M N +='' ，①222AM BN MN += ，1AM =，①3MN BN AB AM +=-=，1BM '= ，设MN x =，则BN =3x -，()22213-x x ∴+=，解得：53x =， 53MN ∴=； （3）AM 2+BN 2＝MN 2，证明如下：如图3，把①BCN 绕点C 顺时针旋转90°得到ACN ' ，①90ACB ∠=︒，AC ＝BC ，①①ABC 是等腰直角三角形，①①CAB ＝①CBA ＝45°，由旋转的性质得，135AN BN CN CN CAN CBN '='=∠'=∠=︒，， ， ①1354590MAN ∠'=︒-︒=︒，①点N '在y 轴上，①①MCN ＝45°，①904545MCN ∠'=︒-︒=︒，①MCN MCN ∠=∠' ，在①MCN 和①MCN ′中，①CN CN MCN MCN CM CM =''⎧⎪∠=∠⎨⎪=⎩，①()MCN MCN SAS ≅' ，①MN MN =' ，在Rt AMN ' 中，222AM AN MN +''= ，①222AM BN MN +＝ ．13．（1）如图1，①90ACB ∠=︒，AE BD ⊥，①90ACB AEB ∠=∠=︒，又①12∠=∠，①CAE CBD ∠=∠；（2）①补全图形如图2；①EF BE =.理由如下：在AE 上截取AM ，使AM BE =.又①AC CB =，CAE CBD ∠=∠，①ΔΔACM BCE ≌，①CM CE =，ACM BCE ∠=∠，又①90ACB ACM MCB ∠=∠+∠=︒，①90MCE BCE MCB ∠=∠+∠=︒，①ME =，又①射线AE 绕点A 顺时针旋转45︒，后得到AF ，且90AEF ∠=︒，①EF AE AM ME BE ==+=.14．解：（1）如图：BD 与EC 的数量关系是相等，理由如下：,AB AC AD AE ==，AB AD AC AE ∴-=-，BD EC ∴=；BD 与EC 的位置关系是垂直，理由如下：AB AC ⊥， 又点,D E 分别在,AB AC 上，BD EC ⊥；（2）成立：理由分别如下：如图：根据旋转的性质可得：,,AD AE AB AC BAD CAE ==∠=∠， ()ABD ACE SAS ∴≌，BD EC ∴=，作BD 的延长线交EC 于点F ，交AC 于点G ，如下图：由ABD ACE SAS △≌△()可知，ABD ACE ∠=∠，AGB FGC ∠=∠，AGB FGC ∴∽，90GAB GFC ∴∠=∠=︒，GF CF ∴⊥，即BD EC ⊥；（3）当点D 在线段BE 上时，90BAD BAC DAC DAC ∠=∠-∠=︒-∠，90CAE DAE DAC DAC ∠=∠-∠=︒-∠，BAD CAE ∴∠=∠，又AB AC =，AD AE =，()BAD CAE SAS ∴∆≅∆，180135ADB AEC ADE ∴∠=∠=︒-∠=︒，451354590BEC AEC ∴∠=∠-︒=︒-︒=︒；（4）由题意知，点D 的轨迹在以A 为圆心，AD 为半径的圆， 在ABD ∆中，当AB 为底时，点D 到AB 的距离最大时，ABD ∆的面积最大， 故如图所示，当AD AB ⊥时，ABD ∆的面积最大，∴旋转角为90︒或270︒，故答案为：90︒或270︒．15．解：（1）在Rt ①ABC 中，BC ＝4，AC ＝2，①ACB ＝90°，AB ∴=在Rt ①BDE 中，BF ＝1，BD ＝2，BE ∴=121tan ,tan 242ED AC EBD ABC BD BC ∴∠==∠=== EBD ABC ∴∠=∠EBD ABD ABC ABD ∴∠-∠=∠-∠ABE CBD ∴∠=∠24AB BE BC BD ===∴①ABE ①①CBD ；（2）当A 、E 、F 三点共线时，分两种情况讨论： ①90AED ∠=︒，如图，在Rt ①AFB 中，222AB BF AF =+21(2)20AE ∴++=2(2)19AE ∴+=2AE ∴=①ABE ①①CBDAE CD ∴=CD ∴= ①如图，90AFB ∠=︒在Rt ①AFB 中，22220119AF AB BF =-=-=AF ∴=2AE AF EF ∴=+=EBD ABC ∠=∠90EBF ABC ∴∠+∠=︒EBF ABC FBC DBF FBC ∴∠+∠+∠=∠++∠24AB BE BC BD ===∴①ABE ①①CBDAE CD ∴=CD ∴=综上所述，CD =CD =（3）如图，延长EF 至点G ，使得EF =FG ，连接BG ，此时①BEG 是等腰三角形， 当G B A 、、三点共线，此时FM 最大//BD GEG DBA ∴∠=∠9090180DBA FBD GBF G FBD GBF ∴∠+∠+∠=∠+∠+∠=︒+︒=︒， 此时，G B A 、、三点共线，F M 、分别是BE 、AE 的中点，FM ∴是①EGA 的中位线，111==()222FM AG AB BG ∴+==16．解：（1）如图①中，(5,0)A ，(0,3)B ，5OA ∴=，3OB =，四边形AOBC 是矩形，3AC OB ∴==，5OA BC ==，90OBC C ∠=∠=︒，矩形ADEF 是由矩形AOBC 旋转得到，5AD AO ∴==，在Rt ADC 中，4CD ，1BD BC CD ∴=-=，(1,3)D ∴．（2）①如图①中，由四边形ADEF 是矩形，得到90ADE ∠=︒，点D 在线段BE 上，90ADB ∴∠=︒，由（①）可知，AD AO =，又AB AB =，90AOB ∠=︒，()Rt ADB Rt AOB HL ∴≌．①如图①中，由ADB AOB ∆≅∆，得到BAD BAO ∠=∠，又在矩形AOBC 中，//OA BC ，CBA OAB ∴∠=∠，BAD CBA ∴∠=∠，BH AH ∴=，设AH BH m ==，则5HC BC BH m =-=-，在Rt AHC 中，222AH HC AC =+，2223(5)m m ∴=+-，175m ∴=， 175BH ∴=， 17(5H ∴，3)． （3）如图①中，当点D 在线段BK 上时，DEK ∆的面积最小，最小值113(522DE DK ==⨯⨯=当点D 在BA 的延长线上时，①D E K ''的面积最大，最大面积113(522D E KD =⨯''⨯'=⨯⨯=． 17．解：（1）∵P AB ∆'由PAC ∆绕点A 旋转得到，∴P AB PAC ∆≅∆'，∴P AB PAC ∠=∠'，P A PA '=，∵60BAC PAC PAB ∠=∠+∠=︒，∴60P AB PAB ∠+∠='︒，即：60P AP ∠='︒，∴旋转角度数为60︒；（2）如图所示，连接P P '，∵60P AP ∠='︒，P A PA '=，∴P AP ∆'为等边三角形，∴6P P PA '==,即点P 与点P '之间的距离为6；（3）在P PB ∆'中，由（1）得：10P B PC ='=，6P P '=，8PB =，∴222P B P P PB ''=+，∴P PB ∆'为直角三角形，∴90P PB ∠='︒，由（1）得60APP ∠='︒，∴150APB P PB APP ∠=∠+='∠'︒，∴APB ∠的度数为150︒．18．（ 1 ）①OA ＝4，①A （4，0），把A （4，0）代入34y x b =-+， 得：b ＝3，过点D 作DH ①AB 于点H ，则DH ＝DO ，BH ＝BO ，①当x ＝0时，y ＝3，①B （0，3），①OA ＝4，BO ＝BH ＝3，在Rt OAB 中，①5AB ，AD ＝DO +OA ＝DH +4， ①1122ABD S AD OB AB DH =⋅⋅=⋅⋅， ①()1143522DH DH ⨯+⨯=⨯⋅， 解得：DH ＝6，①OD ＝6，①点D 的坐标为（﹣6，0），（2）过点P 作PE ①OD 于点E ，则△DPE ①①DBO ，①点P 在直线BD 上，且点P 的横坐标为t ，①DE ＝t +6，①OD ＝6，OB ＝3，在Rt OBD △中，BD ==①①DPE ①①DBO ， ①DP DE DB DO =，66t +，解得：)6DP t =+， ①PC ①BD ， ①①PDC ①①ODB ， ①PC DP OB OD=，①)6236t PC +=，①)6PC t =+，①)()1115154566=22884BCD S BD PC t t t =⋅⋅=⨯+=++； （3）作PH 垂直于x 轴于点H ，设射线EP 绕点E 逆时针旋转45°交x 轴于点K ，顺时针旋转45°交x 轴于点G ．①①BPC ＝90°，①BOC ＝90°①B ，P ，C ，O 四点共圆，①PC PB =,①45PCB PBC ∠=∠=︒，①①POC ＝①PBC ＝45°，①90PHO ∠=︒,①45HPO POC ∠=∠=︒,①PH ＝HO ，①DH ＝6﹣HO ＝6﹣PH ，①DHP DOB ∽, ①663PH DO PH BO -==， 得PH ＝2，①HC ＝CO ＝1，①OE ＝2，①点(0,2)E -,①①KEP ＝①DBC ，①PEB ＝①BDC ，①①KEP +①PEB ＝①DBC +①BDC ，即①KEO ＝①BCO ，①OE ：GK ＝CO ：BO ＝1：3，①GK ＝6，①K （﹣6，0），设直线KE 的解析式为：y kx b =+，则62y k b b =-+⎧⎨-=⎩，解得：132k b ⎧=-⎪⎨⎪=-⎩，， ①直线KE 为：y 13=-x ﹣2， 联立方程组：123334y x y x ⎧=--⎪⎪⎨⎪=-+⎪⎩解得x ＝12，y ＝﹣6，①F 1（12，﹣6），①①KEP +①PEG ＝90°，①①DEG ＝90°，①①OEG ＝①ODE ，①OG ：OE ＝OE ：OD ＝1：3，①OG 23=； ①G （23，0）， 设直线EG 的解析式为：y mx n =+， 则20=32m n n⎧+⎪⎨⎪-=⎩，解得：32m n =⎧⎨=-⎩， ①直线EG 的解析式为：y ＝3x ﹣2， 联立方程组：32334y x y x =-⎧⎪⎨=-+⎪⎩， 解得x 43=，y ＝2， ①F 2（43，2）， 综上所述：F 的坐标为（12，﹣6）或（43，2）． 19．证明：（1）①四边形ABCD 是菱形，①ABC ＝60°， ①AB ＝BC ＝AD ＝CD ，①ADC ＝①ABC ＝60°，①①ADC 是等边三角形，①AD ＝AC ＝AB ＝BC ，①①ACB 是等边三角形，①①ACB ＝①ACD ＝60°，①①ADC ＝①EDF ＝60°，①①ADE ＝①CDF ，①将线段DE 绕点D 逆时针旋转60︒，点E 的对应点为F ， ①DE DF =,在①ADE 和①CDF 中，DA DC ADE CDF DE DF =⎧⎪∠=∠⎨⎪=⎩①①ADE ①①CDF （AAS ），①60DCF DAE ∠=∠=︒,①180DCF BCD ∠+∠=︒，①B ，C ，F 三点共线；（2）如图，过点B 作BH ①AC ，交AG 的延长线于点H ，①BH ①AC ，①①H ＝①GAE ，①ABH ＋①BAC ＝180°，①①ABH ＝120°＝①ACF ，①点G 为BE 的中点，①BG ＝GE ，在①AGE 和①HGB 中，H GAE AGE BGH BG GE ∠=∠⎧⎪∠=∠⎨⎪=⎩，①①AGE ①①HGB （AAS ），由（1）得AE CF =,①AE ＝BH ＝CF ，AG ＝GH ＝12AH ，在①ABH 和①ACF 中，AB AC ABH ACF BH CF =⎧⎪∠=∠⎨⎪=⎩，①①ABH ①①ACF （SAS ），①AF ＝AH ，①AF ＝2AG ．20．（1）如图①CDF 即为旋转之后的图形；（2）证明：由旋转旋转可知：①CAB ①①CFD ，①①CDF =①CBA ，①F =①CAB ，CA =CF ，①①CBA +①CDA =180°，①①CDF +①CDA =180°，①A 、D 、F 三点共线，①AC =CF ，①①F =①CAD ，①①CAB =①CAD ；（3）过点E 作EM ①AF 于点M ，过点C 作CN ①BD 于点N ， ①①ABE =①AME =90°，在①ABE 和①AME 中，EAB EAM ABE AME AE AE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ①①ABE ①①AME （AAS ），①AM =AB =3，BE =ME ，①①ABD =90°，AB =3，BD =4，①5AD ==,①DM =2，设BE EM x ==，则4DN x =-,①()222x 24x +=-，解得 1.5x =，①BE =1.5，DE =2.5， ①12113::225S S BE CN DE CN =⋅⋅=.。

五年级数学下册《旋转后的图形》练习题及答案解析学校:___________姓名：___________班级：______________一、作图题1．画一画。

（1）上图①是轴对称图形的一半。

请以虚线为对称轴，画出它的另一半。

（2）在方格中以线段AB为底边画一个直角三角形。

（3）将画好的三角形向上平移4格。

2．在下面的方格纸上分别画一个三角形，和一个梯形，要求他们的面积都是平行四边形A的面积的一半。

（作图用铅笔）3．画一画。

（1）画出图（1）的对称图形。

（2）将图（2）向右平移4格。

4．下面是边长为1厘米的格子图，请在图上合适位置画一个高3厘米的等腰直角三角形再将它向右平移5格并用实线画出来。

5．画出下面每个图形的另一半，使它成为一个轴对称图形。

6．观察图形，给风车的风叶涂上相应的颜色。

7．把平移后能和图1重合的图形涂上颜色。

8．按要求画一画。

①图形A向下平移4格得到图形B。

①图形A绕点O顺时针旋转90°得到图形C。

①图形A按2①1放大后得到图形D。

9．以直线a为对称轴，画出给定图形的轴对称图形。

10．按要求画图。

把图①绕点O逆时针旋转90°得到图形①。

把图①绕点O顺时针旋转90°得到图形①。

把图①绕点O逆时针旋转90°得到图形①。

11．（1）将下图中三角形先向右平移5格，再向下平移6格。

（2）将下图中梯形沿A点逆时针旋转90度。

二、解答题12．如图，一个三角形与一个平行四边形等底等高，已知平行四边形的面积比三角形的面积大5平方米，这两个图形的面积和是多少平方米？13．先填空，再画平移后的图形。

参考答案与解析：1．见详解【分析】（1）补全轴对称图形的方法：找出图形的关键点，依据对称轴画出关键点的对称点，再依据图形的形状顺次连接各点，画出最终的轴对称图形。

（2）利用三角板，画一条与AB垂直的线段，且A为端点，①A＝90°；最后将两条相互垂直的线段的端点，用第三条线段连接起来，就画好了直角三角形。