量子力学基本公式

普朗克函数反函数普朗克函数 (Planck function) 是物理学中一个用于描述热辐射的函数，它由德国物理学家普朗克 (Max Planck) 创立。

普朗克函数的反函数也是物理学研究中的一个重要部分。

一、普朗克函数的定义普朗克函数是指一个与温度，波长和辐射强度相关的函数。

它通常用于描述黑体辐射过程中的能量分布和辐射强度的密度。

普朗克函数被广泛地应用于天体物理学、气象学、空间科学、核物理学等领域，因为它能帮助科学家们更好地理解和解释物质的热量特性。

二、普朗克函数的特性普朗克函数被定义为：$$B(\nu, T) =\frac{2h\nu^3}{c^2}\cdot\frac{1}{e^{\frac{h\nu}{k_bT}}-1}$$其中，$B(\nu, T)$ 表示在温度为 $T$ 的黑体内，频率为 $\nu$ 的辐射强度密度，$h$ 表示普朗克常数，$c$ 表示光速，$k_b$ 表示玻尔兹曼常数。

普朗克函数有以下几个特点：1. 频率越高，辐射强度密度越大。

2. 在短波长处，普朗克函数函数值急剧上升，而且在极短波长处，函数值趋近于无穷大。

3. 随着温度的升高，普朗克函数曲线向短波长方向移动，且曲线最大值也会向短波长方向移动。

三、普朗克函数反函数的意义普朗克函数反函数，也称为辐射定律，是指一个从辐射强度密度到温度之间的关系式。

它是普朗克函数的逆运算，意义重大。

普朗克函数反函数的求解可以帮助我们在物理学领域中解决很多实际的问题。

例如，它可以被用来计算太阳辐射的温度、判断天体运动的情况等等。

四、普朗克函数反函数的公式普朗克函数反函数字面上的意思是一个可以将辐射强度密度转化为温度的函数。

它可以用下面这个公式进行求解：$$T = \frac{h\nu}{k_b{ln(\frac{2h\nu^3}{Ic^2}+1)}}$$其中，$T$ 表示温度，$I$ 表示辐射强度密度，$\nu$ 表示频率，$h$ 表示普朗克常数，$c$ 表示光速，$k_b$ 表示玻尔兹曼常数。

量子力学公式
量子力学中的一些常见公式包括：
1. 薛定谔方程式：描述了量子物理学的宏观世界，即微观粒子如何随着时间的推移而演变。

其一般形式为：iℏ∂Ψ/∂t=HΨ，其中i是虚数单位，ℏ是普
朗克常数的约化常数，Ψ是波函数，H是哈密顿算符。

2. 波粒二象性：描述了物质粒子的波动性质和粒子性质之间的相互作用关系。

其表达式为λ=h/p，其中λ是波长，h是普朗克常数，p是粒子的动量。

3. 测量理论：物理量的测量和观测结果有一定的概率性和不确定性。

测量理论采用概率统计的方法来描述这种不确定性。

最常见的公式是海森堡不确定性原理：ΔxΔp≥h/4π，其中Δx和Δp分别表示位置和动量的不确定度，h 是普朗克常数。

4. 费米-狄拉克统计和玻色-爱因斯坦统计：描述了物质粒子的统计行为。

费米-狄拉克统计用于描述费米子（如电子、质子等）的行为，玻色-爱因斯坦统计用于描述玻色子（如光子、声子等）的行为。

5. 波函数的复共轭：Ψ^（r，t）。

6. 归一化条件：∫Ψ（r，t）^2d3r=1。

7. 位置算符：x。

8. 动量算符：-iℏ∇。

9. 能量算符：iℏ∂/∂t。

10. 完备性条件：∫ψn^（r）ψm（r）d3r=δnm。

以上公式仅供参考，如需更准确的信息，建议查阅量子力学相关的书籍或咨询专业人士。

量子力学角动量公式量子力学中的角动量公式，就像是一把神奇的钥匙，能为我们打开微观世界的神秘大门。

在我们日常生活的宏观世界里，对于物体的转动和角动量的理解相对直观。

比如说，一个旋转的陀螺，我们能清楚地看到它的转动。

但在微观世界中，角动量的概念和表现可就大不相同啦。

咱先来说说量子力学角动量的基本公式：$J^2 = j(j + 1)\hbar^2$ 以及 $J_z = m_j\hbar$ 。

这里的 $j$ 代表角量子数，$m_j$ 则是磁量子数，而 $\hbar$ 是约化普朗克常数。

记得有一次，我给学生们讲解这个公式的时候，有个小家伙一脸迷茫地问我：“老师，这东西看不见摸不着的，学它有啥用啊？”我笑着跟他们说：“同学们，就好比你们在玩拼图，每一块拼图看起来没啥特别，但当它们都拼在一起，就能呈现出一幅完整美丽的画面。

量子力学的角动量公式也是这样，虽然单个看起来有点复杂和抽象，但当它和其他的知识结合起来，就能让我们理解原子、分子，甚至是整个微观世界的运行规律。

”那咱们再深入一点聊聊这个公式。

在量子力学里，角动量不再是像宏观世界那样连续变化的，而是离散的、量子化的。

这就好比上楼梯，你只能站在特定的台阶上，而不能处于两个台阶之间的位置。

比如说氢原子中的电子，它的角动量就遵循这些公式。

电子的状态不是随意的，而是由特定的角量子数和磁量子数决定。

这就决定了电子能处于哪些特定的轨道，从而影响着原子的化学性质和物理性质。

再举个例子，在研究晶体结构的时候，角动量公式也发挥着重要作用。

晶体中的原子或者离子的排列方式，与它们的角动量特性息息相关。

想象一下，我们就像是微观世界的探险家，而角动量公式就是我们手中的地图和指南针。

它指引着我们在这个充满神秘和奇妙的微观领域中前行，让我们能够揭示那些隐藏在微小尺度下的奥秘。

总之，量子力学角动量公式虽然看似复杂难懂，但它却是我们探索微观世界的有力工具。

只要我们用心去理解，去探索，就能发现它背后所蕴含的无尽奥秘和美妙。

海森堡公式海森堡公式是量子力学中的一个基本公式，由德国物理学家海森堡于1925年提出。

它描述了物理量的变化与时间的关系，是量子力学中的基本原理之一。

海森堡公式的数学表达是：ΔAΔB≥h/2π，其中ΔA和ΔB分别表示物理量A和B的不确定度，h为普朗克常数，π为圆周率。

这个公式表明，对于量子系统来说，无法同时精确地测量两个不对易的物理量，其不确定度存在一定的下限。

海森堡公式的提出，揭示了量子世界的基本规律，与经典物理学中的牛顿定律有着本质的区别。

在经典物理学中，我们可以精确地测量物体的位置和动量，这两个物理量是对易的。

而在量子力学中，海森堡公式告诉我们，对于量子粒子来说，位置和动量是不对易的，无法同时精确地测量。

海森堡公式的意义不仅仅在于揭示了物理量的测量限制，还为量子力学提供了一种全新的解释和理解方式。

根据海森堡公式，我们知道测量的过程会对系统产生干扰，从而使得测量结果不确定。

这一观点引发了著名的“测不准原理”，即测量的不确定性是量子力学的本质特征之一。

海森堡公式也为量子力学的发展提供了理论基础。

在实际应用中，海森堡公式可以用来推导各种物理量之间的关系，帮助我们理解和解释实验现象。

例如，在核物理中，海森堡公式可以用来推导能量和时间的不确定关系，从而解释核反应的过程。

除了在理论研究中的应用，海森堡公式在实际技术中也有重要的作用。

例如，在核磁共振成像技术中，海森堡公式可以用来解释和优化图像的分辨率。

通过调节测量的物理量，可以在一定程度上提高图像的清晰度。

海森堡公式是量子力学中的一个基本公式，揭示了物理量测量的不确定性，并为量子力学的发展提供了理论基础。

它不仅在理论研究中有重要应用，还在实际技术中发挥着重要作用。

通过深入理解和应用海森堡公式，我们可以更好地理解和解释量子世界的规律。

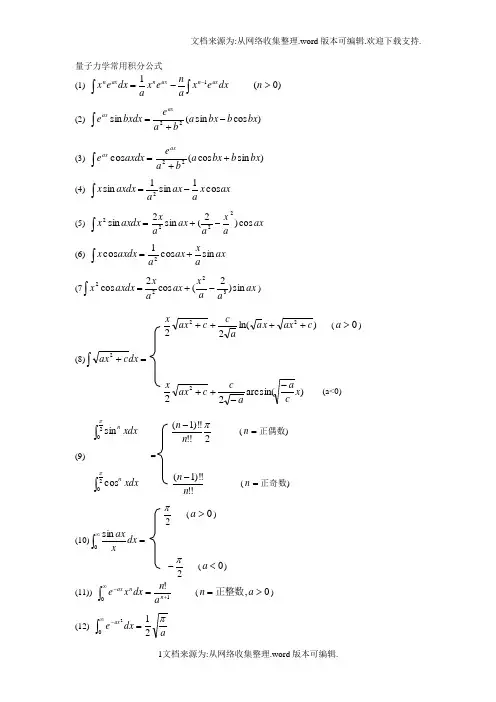
基本公式简要第一章▲p h =λ h E =ν▲()()1r d r 32=⎰全 ψ▲()()()p d e p 21r 3r p i 23 ⋅⎰=ϕπψ ()()()r d e r 21p 3r p i 23 ⋅-⎰=ψπϕ ▲()()r d r Aˆr A 3* ψψ⎰= ▲∇-= i p ˆ p ˆr l ˆ ⨯= t i E ˆ∂∂= ()r V m2H 22+∇-=▲()()()t ,r r V m 2t ,r ti 22ψψ⎥⎦⎤⎢⎣⎡+∇-=∂∂ ▲()()()t ,r t ,r t ,r *ψψρ= ()()**m2i t ,r j ψψψψ∇-∇-=⎰⋅-=⎰s s d j d dtdτρτ ▲()() iEt E e r t ,r -=ψψ▲()()()r E r r V m 2E E 22 ψψ=⎥⎦⎤⎢⎣⎡+∇- ()()r E r H ˆE E ψψ=▲()()t iE n nn n e r C t ,r -∑=ψψ第二章▲无限深势阱 ,3,2,1n ,ma2nE 2222n ==π()a x 0ax ,0x ,0,a x n sin a 2x n <<⎪⎩⎪⎨⎧><⎪⎭⎫ ⎝⎛=πψ▲方势垒的反射与透射反射系数=i r j j透射系数i t j j T =()E V ,E V m 200>-= κ1a >>κ,()()(),E V m 2a 2exp V E V E 16T 020 ---≈ ▲方势阱的反射,透射(),E V m 2k 0 +=',V E 1V E 4a k sin 1T 002⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+'+= 共振透射 ,3,2,1n ,n a k =='π,1T =, ,3,2,1n ,ma2n V E 22220n =+-=π▲δ势()x ψ'的跃变条件 ()()()02002ψγψψm ='-'-+ δ势阱()()x x V γδ-= ()0>γ中的束缚态()LxeL 1x -=ψ222m Eγ-= γm L 2 =▲一维谐振子()22x 21x V μω=()ω 21+==n E E n ,,,2,1,0 =n()()x H e A x n 2x n n 22αψα-=，()()mnnmdx x x δψψ=⎰+∞∞-，()()()x x nnnψψ1-=-第三章▲[]αββαδ i p x =ˆ, [],x i x ,l ˆγαβγβαε =[]γαβγβαεp i p ,l ˆ= []γαβγβαεl ˆi l ˆ,l ˆ = ▲,i lˆz ϕ∂∂-= .sin 1sin sin 1l ˆ22222⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂∂-=ϕθθθθθ 222r 22222222222mr2lˆm 2p ˆmr 2l ˆr r r 1m 2mr 2l ˆr r r r 1m 2T ˆ +=+∂∂-=+∂∂∂∂-= 径向动量算符⎪⎭⎫⎝⎛+∂∂-=r r i p r 1ˆ▲1A ˆA ˆA ˆA ˆ11==-- ().BˆB ˆA ˆ111A ˆ---= ▲转置算符*A ˆd Aˆ~*d ψτϕϕτψ⎰=⎰，()~A ˆ~B ˆB ˆA ˆ~=. ▲Aˆ厄米共轭算符+A ˆ ()()ϕψϕψ,A ˆA ˆ,=+,*ˆ~ˆAA=+()++++=A B C AC B A ˆˆˆˆˆˆˆ ▲ 厄米算符()()ϕψϕψ,A ˆAˆ,=, 或AˆAˆ=+().,m n n m δψψ=▲力学量A ˆ涨落()()⎰-=-=τψψ∆d A A ˆA A ˆA 2*22▲ϕ∂∂-= i l ˆz本征函数()ϕπϕψim e 21=, ,2,1,0±±=mx i p x ∂∂-= ˆ 本征态()()x p i x p xxe x ''=πψ21x p ':+∞<'<∞-x p (连续变化) ()()()x x p *p p p dx x x xx''-'='+∞∞-'⎰δψψ()z 2l ,l的正交归一共同本征函数()()()()()()ϕθπϕθim m l mlm e cos P !m l !m l 41l 21,Y +-⋅+-=. lm Y 称为球谐函数，它们满足()lm 2lm 2Y 1l l Y l ˆ +=， ,Y m Y l ˆlm lm z = ,l ,1l ,,1l ,l m ,,2,1,0l -+--==,Y Y d sin d m m l l m l *lm20''''=⎰⎰δδθθϕππ▲不确定关系()()[]B ˆ,A ˆ21B A 22≥∆∆ []B ˆ,A ˆ21B A ≥∆∆ 2p x x ≥∆∆▲∑=αααψψa , ()ψψαα,a =▲()()xx ik 0e dk 21x x -∞+∞-⎰=-πδ,()()()()⎰='-''∞+∞-'-''x p p i x e d21p p πδ▲箱归一化LnhL n 2p p n ===π , ()Lnx i x ip p eL1e L 1x nnπψ==第四章▲()[]tAH ,A i 1t A dt d ∂∂+== ▲位力定理V r p m1T 22∇⋅==▲对称变换Q :I QQ Q Q ==++1Q Q -+=平移x δ的算符()[],p ˆx i exp x x exp x D x δδδ-=⎥⎦⎤⎢⎣⎡∂∂-=空间旋转δϕ算符()[],l ˆi exp exp R z δϕϕδϕδϕ-=⎥⎦⎤⎢⎣⎡∂∂= ▲ψψ+=ij P (ψ称为对称波函数) ψψ-=ij P (ψ称为反对称波函数)()()()()()[]()()(),q q P 121q q q q 21q ,q 2k 1k 121k 2k 2k 1k 21S k k 21212121ϕϕϕϕϕϕψ+=+=()()()()()[]()()()()()()().q q P 121q q q q 21q q q q 21q ,q 2k 1k 122k 1k 2k 1k 1k 2k 2k 1k 21Ak k 212211212121ϕϕϕϕϕϕϕϕϕϕψ-==-=第五章 ▲哈密顿量()()()r V r2l r r r 2r V r 2l 2p r V 2H 22222222r 22++∂∂-=++=+∇-=μμμμμ ▲能量本征方程：()ψψμμE r V r 2lr r r 222222=⎥⎦⎤⎢⎣⎡++∂∂- 径向波函数()r R l 满足的方程：()()()()()()0r R r 1l l r V E 2dr r dR r 2dr r R d l 22l 2l 2=⎪⎭⎫⎝⎛+--++ μ ()1l 2f l+=()()r r r R l l χ= ()()()()()0r r 1l l r V E 2r l 22l =⎪⎭⎫⎝⎛+--+"χμχ ▲质心运动()()R E R M2CT 2R 2φφ=∇-相对运动()()()C T 22E E E ,r E r r V 2-==⎥⎦⎤⎢⎣⎡+∇-ψψμ▲无限深球方势球 s 态()0l =： ()()()()0r r V E 2r l 2l =-+"χμχ(),000=χ().0a 0=χ (),2,1,0n ,a21n E r 22r 220n r =+=μπ()(),a r 0,ar 1n sin a 2r r 0n r ≤≤+=πχ ()[]1dr r 2a0n r =⎰χ0l ≠情况： ()(),a k ,r k j C r R l n l n l n l l n l n r r r r r ξ==球贝塞尔函数()()ρρπρ21l l J 2j +=()().dr r r R r R a 0n n 2R l n r r l r n r ⎰=''δ,,2,1,0n ,a2E r 2ln 22l n r r==ξμ ▲ 三维各向同性谐振子 ()22r 21x V μω=()()22r 2r ll n r ,23l ,n F er ~r R 22r αα+--().,2,1,0l ,n ,23N E E r N =+==ωl n 2N r +=()()2N 1N 21f N ++=▲ 氢原子 ()()ξξξ,2l 2,1l n F N r R 2l nl nl +++-=-e()()()ϕθϕθψ,Y r R ,,r lm nl nlm =,,3,2,1n ,n 1a 2e n12e E E 22224n =-=-==μ2n nf =径向概率密度()r P =()2nl r χ1n l -=,称为“圆轨道”:无节点0n r =.,nar n 1n ,n er --∝χ, 最可几半径n r ：()21nn r -χ极大值所在的位置为,,3,2,1n ,a n r 2n ==[][] i ,i l ,z =∂∂-=ϕϕϕ绕z 轴的环电流密度2nlm sin r 1me j ψθμϕ -=磁矩m c 2m e M B z μμ-=-= c2e B μμ=1g l -≡l zg m M =若取c 2e μ为单位,则l zg m M =. 类氢离子()r Ze r V 2-= ,,3,2,1n ,nZ 2e E 2224n =-=μ径向波函数与氢原子径向波函数形式相同,只是将波尔半径a 换成Z a .。

量子力学公式速查手册粒子波动与精确测量的关联公式量子力学公式速查手册：粒子波动与精确测量的关联公式引言：量子力学是描述微观世界的基本理论，它以精确的数学公式表达粒子的波动性和测量结果之间的关联。

本文将为读者提供一个量子力学公式速查手册，重点关注粒子的波动性和精确测量相关的公式。

一、波粒二象性：1. 德布罗意波长公式：λ = h / p其中，λ表示波长，h表示普朗克常量，p表示粒子的动量。

2. 庞加莱不确定性原理：Δx × Δp ≥ h / 4π其中，Δx表示位置的不确定性，Δp表示动量的不确定性，h为普朗克常量。

3. 束缚态电子处于稳定轨道的条件：2πr = nλ其中，r表示电子轨道半径，n表示整数，λ为电子的德布罗意波长。

二、精确测量：1. 基态能量的测量精度：ΔE ≥ h / 2π其中，ΔE表示能量的不确定性。

2. 哈耳特测量的不确定性原理：ΔH × Δt ≥ h / 2π其中，ΔH表示能量的测量不确定性，Δt表示时间的不确定性。

三、哈密顿运算量公式：1. 总能量的哈密顿量公式：Ĥ = K + V其中，Ĥ表示哈密顿算符，K为动能算符，V为势能算符。

2. 动能算符的表达式：K = - (h²/2m) ∇²其中，K表示动能算符，h为约化普朗克常量，m为粒子的质量，∇²表示拉普拉斯算子。

四、薛定谔方程：1. 薛定谔方程的一般形式：ĤΨ = EΨ其中，Ĥ表示哈密顿算符，Ψ为波函数，E表示能量。

2. 粒子自旋的薛定谔方程：ĤΨ = (E - μ̅B)Ψ其中，Ĥ表示哈密顿算符，Ψ为波函数，E表示能量，μ̅为磁矩，B表示磁场。

结论：量子力学公式速查手册包含粒子波动和精确测量相关的重要公式，它们帮助我们理解微观世界的行为并提供精确的数学描述。

熟练掌握这些公式，可以在研究和应用量子力学时为我们提供准确的理论基础。

希望本文能为读者提供便利，并在学习和研究量子力学过程中起到指导作用。

量子计量计算公式量子计量是一种用于描述和预测微观粒子行为的理论框架，它是量子力学的一个重要组成部分。

量子计量计算公式则是用来计算量子系统状态和性质的数学工具，它能够帮助我们理解和预测微观世界的现象。

在本文中，我们将介绍一些常见的量子计量计算公式，并探讨它们在量子力学中的应用。

首先，让我们来看看量子力学中最基本的公式之一——薛定谔方程。

薛定谔方程描述了量子系统的时间演化，它的数学表达式为：\[i\hbar\frac{\partial}{\partial t}\Psi(\mathbf{r},t) = \hat{H}\Psi(\mathbf{r},t)\]其中，\(\Psi(\mathbf{r},t)\)是波函数，描述了量子系统的状态；\(\hat{H}\)是哈密顿算符，描述了系统的能量。

这个方程告诉我们，波函数随时间的演化是由哈密顿算符所决定的，它是量子系统动力学的基础。

接下来，我们来看看量子系统的测量。

在量子力学中，测量是一个非常重要的概念，它允许我们观察和获取量子系统的信息。

在进行测量时，我们需要用到投影算符。

投影算符可以将波函数投影到某个特定的测量结果上，它的数学表达式为：\[\hat{P}_\lambda = \sum_n |\lambda_n\rangle\langle\lambda_n|\]其中，\(\lambda\)表示测量结果，\(|\lambda_n\rangle\)表示对应于测量结果\(\lambda\)的本征态。

投影算符的作用是将波函数投影到测量结果\(\lambda\)对应的本征态上，这样我们就可以得到测量结果\(\lambda\)的概率。

除了测量外，我们还需要考虑量子系统的平均性质。

在量子力学中，平均性质可以用期望值来描述，它的数学表达式为：\[\langle\hat{A}\rangle = \langle\Psi|\hat{A}|\Psi\rangle\]其中，\(\hat{A}\)是描述某个物理量的算符，它对应于可观测量；\(\Psi\)是波函数。

量子计算精确计算公式量子计算是一种基于量子力学原理的计算模型，它利用量子比特的叠加和纠缠特性来进行计算，相比传统计算模型，量子计算具有更强的并行性和计算能力。

在量子计算中，精确计算公式是非常重要的，它可以帮助我们准确地描述量子系统的演化和性质。

本文将介绍一些常见的量子计算精确计算公式，并讨论它们在量子计算中的应用。

1. 薛定谔方程。

薛定谔方程是描述量子系统演化的基本方程，它可以用来计算量子系统的波函数随时间的演化。

薛定谔方程的一般形式为：iħ∂Ψ/∂t = HΨ。

其中，Ψ是系统的波函数，H是系统的哈密顿量，i是虚数单位，ħ是普朗克常数。

薛定谔方程可以精确地描述量子系统的演化，包括系统的能级结构、波函数随时间的演化等。

2. 波函数的归一化条件。

在量子力学中，波函数的归一化条件是非常重要的，它可以帮助我们确定量子系统的态。

波函数的归一化条件可以用来计算系统的概率分布，以及系统的平均性质。

波函数的归一化条件的一般形式为：∫|Ψ|²dV = 1。

其中，Ψ是系统的波函数，dV是系统的体积元。

波函数的归一化条件可以帮助我们确定系统的态，并计算系统的性质。

3. 哈密顿量的本征值方程。

在量子力学中，哈密顿量的本征值方程是描述系统能级结构的重要方程。

哈密顿量的本征值方程可以用来计算系统的能级和能级之间的跃迁。

哈密顿量的本征值方程的一般形式为：HΨ = EΨ。

其中，H是系统的哈密顿量，Ψ是系统的波函数，E是系统的能级。

哈密顿量的本征值方程可以帮助我们确定系统的能级结构，以及计算系统的能级。

4. Heisenberg不确定性原理。

Heisenberg不确定性原理是量子力学中的基本原理之一，它描述了位置和动量之间的不确定性关系。

Heisenberg不确定性原理可以用来计算系统的不确定性，以及系统的测量误差。

Heisenberg不确定性原理的一般形式为：ΔxΔp ≥ħ/2。

其中，Δx是位置的不确定性，Δp是动量的不确定性，ħ是普朗克常数。