20力学量算符和量子力学公式的矩阵表示
- 格式:ppt
- 大小:394.01 KB
- 文档页数:15






量子力学中的量子力学力学量的表示量子力学是描述微观世界的物理学理论,它提供了一种描述粒子性质的数学框架。
在量子力学中,力学量是描述系统状态的物理量。
本文将探讨在量子力学中,如何表示力学量以及不同力学量的物理意义。
一、力学量的表示在经典物理学中,力学量通常可以用数值来表示,例如质量、速度、位移等。
然而,量子力学中的力学量不能简单地用数值表示,而是需要用算符表示。
力学量的算符通常用大写字母表示,比如位置算符X,动量算符P等。
对于某个具体的力学量,它的算符作用在波函数上,得到的结果是该力学量对应的本征值乘以波函数。
这可以用数学表达式表示为:AΨ = aΨ其中A是力学量的算符,Ψ是波函数,a是力学量的本征值。
这个方程称为力学量的本征值方程。
二、不同力学量的表示1. 位置算符在量子力学中,粒子的位置可以用位置算符X来表示。
位置算符的本征态是位置本征态,它表示粒子在某个确定的位置。
对于一维情况,位置本征态的波函数可以写为:Ψ(x) = δ(x - x0)其中x0是位置本征态对应的位置。
2. 动量算符动量算符P描述粒子的运动状态。
动量算符的本征态是动量本征态,它表示粒子具有某个确定的动量。
对于一维情况,动量本征态的波函数可以写为:Ψ(p) = e^(ipx/ħ)其中p为动量本征态对应的动量,ħ为普朗克常数除以2π。
3. 能量算符能量是量子力学中的另一个重要的力学量。
能量算符H描述粒子的能量状态。
能量算符的本征态是能量本征态,它表示粒子具有某个确定的能量。
能量本征态的波函数可以写为:Ψ(E) = e^(-iEt/ħ)其中E为能量本征态对应的能量,t为时间。
三、力学量的测量和物理意义在量子力学中,力学量的测量是通过对算符的作用得到的本征值来实现的。
当对某个力学量进行测量时,系统将处于该力学量的某个本征态上,从而得到相应的本征值。
力学量的本征值对应着可能的测量结果。
例如,对位置算符进行测量,可以得到粒子的位置值;对动量算符进行测量,可以得到粒子的动量值。
§4.5 量子力学的矩阵形式和表象变换态和力学量算符的不同表示形式称为表象。
态有时称为态矢量。
力学量算符对态的作用实际上是对矢量量进行变换,因此可与代数中线性变换进行类比。
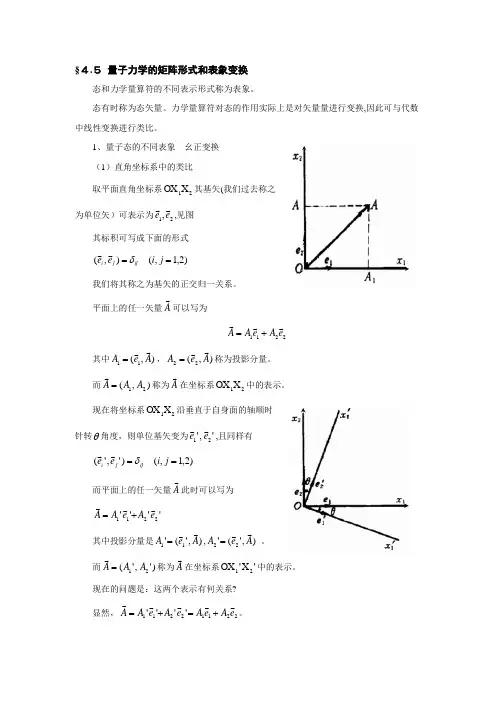
1、量子态的不同表象 幺正变换 (1)直角坐标系中的类比取平面直角坐标系21X OX 其基矢(我们过去称之为单位矢)可表示为21,e e,见图其标积可写成下面的形式)2,1,(),(==j i e e ijj i δ我们将其称之为基矢的正交归一关系。
平面上的任一矢量A可以写为2211e A e A A +=其中),(11A e A =,),(22A e A=称为投影分量。
而),(21A A A = 称为A在坐标系21X OX 中的表示。
现在将坐标系21X OX 沿垂直于自身面的轴顺时针转θ角度,则单位基矢变为','21e e,且同样有)2,1,()','(==j i e e ijj i δ而平面上的任一矢量A此时可以写为 ''''2211e A e A A +=其中投影分量是),'('11A e A =,),'('22A e A=。
而)','(21A A A = 称为A在坐标系'X 'OX 21中的表示。
现在的问题是:这两个表示有何关系?显然,22112211''''e A e A e A e A A+=+=。
用'1e 、'2e分别与上式中的后一等式点积(即作标积),有),'(),'('2121111e e A e e A A+= ),'(),'('2221212e e A e e A A+=表成矩阵的形式为⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛212212211121),'(),'(),'(),'(''A A e e e e e e e e A A由于'1e 、1e 及'2e 、2e的夹角为θ,显然有⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛21212212211121cos sin sin cos ),'(),'(),'(),'(''A A A A e e e e e e e e A A θθθθ或记为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛2121)(''A A R A A θ 其中⎪⎪⎭⎫⎝⎛-=θθθθθcos sin sin cos )(R 是把A在两坐标中的表示⎪⎪⎭⎫ ⎝⎛''21A A 和⎪⎪⎭⎫⎝⎛21A A 联系起来的变换矩阵。

量子力学考试试题(附答案)1.束缚于某一维势阱中的粒子,其波函数由下列诸式所描述:()()()023cos 222ikx L x x x L L x Ae x L L x x ψπψψ=<-=-<<=>(a )、求归一化常数A,(b )、在x=0及x=L/4之间找到粒子的概率为何? 解:(a )由波函数的归一化条件()222222222331coscos 33cos cos 3cos 6cos 126sin 262ikx ikx ikx ikx LLx x x dx Ae Ae dx L Lx x A e e dxL L x A dx L A x dx L A L x x L A L ππψππππππ∞∞-∞-∞∞--∞∞-∞∞-∞-====⎛⎫=+ ⎪⎝⎭⎛⎫=+ ⎪⎝⎭=⎰⎰⎰⎰⎰于是:A =(b)()224406sin 0.196926LL A L x x dx x L πψπ⎛⎫=+= ⎪⎝⎭⎰2、证明在定态中,概率流密度与时间无关。
证:对于定态,可令)]()()()([2 ])()()()([2 )(2 )( )()()(******r r r r mi e r e r e r e r m i mi J e r t f r t r Et i Et i Et iEt i Etiψψψψψψψψψψ∇-∇=∇-∇=ψ∇ψ-ψ∇ψ===ψ-----)()(, 可见t J 与无关。
4、波长为1.0*10-12m 的X 射线投射到一个静止电子上,问在与入射光成60o 角的方向上,探测到散射光的波光为多少?解:由公式 22sin 2c θλλλ'-=其中:120 2.43102ch m m cλ-==⨯可得:1212212601.0102 2.4310sin 1.215102λλλ---''-=-⨯=⨯⨯⨯=⨯ 01212212601.0102 2.4310sin 1.215102λλ---'-=-⨯=⨯⨯⨯=⨯122.21510m λ-=⨯。

量子力学中的矩阵表示方法量子力学是一门探索微观世界的科学,而矩阵表示方法是量子力学中非常重要的一部分。
通过矩阵表示方法,我们能够描述和计算微观粒子的性质和相互作用。
本文将介绍矩阵表示方法在量子力学中的应用,以及其背后的数学原理。
首先,我们来了解一下量子力学中的态。
在量子力学中,粒子的态可以通过波函数来描述。
波函数是一个复数函数,在给定的时刻和空间点上,它代表了粒子的状态。
对于多粒子系统,其波函数包含多个变量,比如位置和自旋等。
然而,波函数并不是常用的物理量,我们更关注的是物理量的平均值和概率分布。
而在量子力学中,物理量是由算符来表示的。
算符是一种对波函数作用的数学对象,它可以描述某个物理量的性质。
量子力学中最常用的算符就是哈密顿算符,它表示了系统的总能量。
接下来,我们讨论如何将算符用矩阵表示。
矩阵表示方法是量子力学中一种非常常用的计算工具。
它的基本思想是将量子力学中的算符映射为矩阵,从而可以方便地对波函数进行计算和分析。
对于一个算符A,我们可以将其对应的矩阵表示为A。
矩阵A的元素A(i,j)表示了算符A在波函数基矢量|i⟩和|j⟩之间的矩阵元。
矩阵元代表了算符A在不同态之间的跃迁概率。
通过矩阵表示方法,我们可以方便地进行算符之间的运算。
例如,两个算符A和B的乘积AB可以通过将它们对应的矩阵相乘来得到。
这样,我们就能够方便地计算复杂的量子力学表达式。
除了表示算符,矩阵表示方法还可以用于描述量子态之间的变换。
量子力学中的变换由幺正算符来表示,而幺正算符可以看作是保持态空间长度不变的线性变换。
幺正算符对应的矩阵是正交矩阵,它满足矩阵的厄米共轭等于其逆矩阵。
通过矩阵表示方法,我们可以方便地描述和求解量子系统的本征态和本征值。
对于一个算符A,如果满足A|i⟩=a(i)|i⟩,其中|i⟩是A的本征态,a(i)是对应的本征值,那么算符A对应的矩阵A的特征方程就是AΨ=aΨ。
通过求解特征方程,我们可以得到算符A的本征值和本征态。

量子力学中的量子力学算符量子力学中的量子力学算符是描述量子系统性质的重要工具。
它们代表了物理量的数学运算符,用于计算和预测系统的态矢量的演化和测量结果。
本文将介绍量子力学算符的基本概念、性质和应用。
1. 算符的定义在量子力学中,算符是表示物理量的数学运算符。
它们作用于态矢量,用于计算物理量的测量结果或表示系统的演化。
量子力学算符通常用大写字母表示,例如位置算符X、动量算符P和能量算符H等。
2. 算符的性质量子力学算符具有多个重要性质,包括线性性、厄米性和厄米算符的本征值问题。
2.1 线性性:量子力学算符是线性的,即对于任意常数a和b,有F(aψ + bφ) = aF(ψ) + bF(φ),其中F表示任意量子力学算符。
2.2 厄米性:厄米性是量子力学算符的重要性质。
一个算符F的厄米共轭算符F†定义为满足内积关系⟨ψ|F†φ⟩ = ⟨Fψ|φ⟩的算符。
对于厄米算符F,其本征值都是实数。
2.3 厄米算符的本征值问题:对于厄米算符F,存在一组完备正交本征态{φn},其对应的本征值{fn}都是实数。
即Fφn = fnφn。
这个本征值问题是量子力学中重要的数学工具,可以用于计算物理量的测量结果和态矢量的演化。
3. 常见的量子力学算符量子力学中存在着许多常见的算符,这些算符用于描述各种物理量和系统性质。
3.1 位置算符X:位置算符X表示粒子在空间中的位置。
对于一维情况,位置算符的本征态是位置空间的波函数;对于三维情况,位置算符的本征态是位置空间的波函数。
3.2 动量算符P:动量算符P表示粒子的动量。
对于一维情况,动量算符的本征态是动量空间的波函数;对于三维情况,动量算符的本征态是动量空间的波函数。
3.3 能量算符H:能量算符H表示粒子的能量。
它是量子体系的哈密顿算符,其本征态是能量空间的波函数。
4. 算符的应用量子力学算符在物理学中有广泛的应用。
它们可以用于计算各种物理量的期望值、计算系统的演化和描述量子力学中的各种现象。
Dirac符号系统与表象一、Dirac符号1.引言我们知道任一力学量在不同表象中有不同形式,它们都是取定了某一具体的力学量空间,即某一具体的力学量表象。
量子描述除了使用具体表象外,也可以不取定表象,正如几何学和经典力学中也可用矢量形式A来表示一个矢量,而不用具体坐标系中的分量(Ax ,Ay,Az)表示一样。
量子力学可以不涉及具体表象来讨论粒子的状态和运动规律。
这种抽象的描述方法是由Dirac首先引用的,本质是一个线性泛函空间,所以该方法所使用的符号称为Dirac 符号。
2.(1).(或基组)(2(3<ψ|按定义有:ψψa)在同一确定表象中,各分量互为复共轭;b)由于二者属于不同空间所以它们不能相加,只有同一空间的矢量才能相加;c)右矢空间任一右矢可以和左矢空间中任一左矢进行标积运算,其结果为一复数。
(4).本征函数的封闭性a)分立谱展开式:可得:因为|ψ>是任意态矢量,所以:b)连续谱对于连续谱|q>,q取连续值,任一状态|ψ>展开式为:因为|ψ>是任意态矢量,所以:这就是连续本征值的本征矢的封闭性。
c )投影算符|Q n ><Q n |或|q><q|的作用相当一个算符,它作用在任一态矢|ψ>上,相当于把|ψ>投影到左基矢|Q n >或|q>上,即作用的结果只是留下了该态矢在|Q n >上的分量<Q n |ψ>或<q|ψ>。
故称|Q n ><Q n |和|q><q|为投影算符。
因为|ψ>在X 表象的表示是ψ(x,t),所以显然有:在分立谱下:所以*(')()(')n n nu x u x x x δ=-∑。
在连续谱下:所以*(')()(')u ⎰。
3.(1X 即Q (2即有:4.到目前为止,体系的状态都用坐标(x,y,z)的函数表示,也就是说描写状态的波函数是坐标的函数。
量子力学知识总结认真、努力、坚持、反思、总结…物理111 杨涛量子力学知识点小结一、绪论1.光的粒子性是由黑体辐射、光电效应和康普顿效应(散射)三个实验最终确定的。
2.德布罗意假设是任何物质都具有波粒二象性,其德布罗意关系为E h ν=和h p n κλ==3.波尔的三个基本假设是定态条件假设、n mE E h ν-=频率条件假设、化条件)(索末菲等推广的量子21或量子化条件假设⎰⎰+==h n pdq nh pdq )(4.自由粒子的波函数()ip r Et Aeψ⋅-=5.戴维孙革末的电子在晶体上衍射实验证明了电子具有波动性。
二、波函数及薛定谔方程(一)波函数的统计解释(物理意义)A.波函数(,)r t ψ的统计解释2(,)r t d t r ψτ表示时刻在点位置处单位体积内找2sin d r drd d τθϕθ=到粒子的几率(注:)。
B. 波函数(,,,)x y z t ψ的统计解释2(,,,),,x y z t dxdydz t x y z ψ表示时刻在点()位置处单位体积没找到粒子的几率。
例:已知体系处于波函数(,,)x y z ψ所描写的状态,则在区间[,]x x dx +内找到粒子的概率是2(,,)x y z dydz dx ψ+∞+∞-∞-∞⎡⎤⎢⎥⎣⎦⎰⎰. 已知体系处于波函数(,,)r ψθϕ所描写的状态,则在球壳r r dr →+内找到粒子的概率是22200(,,)sin r d d r dr ππψθϕθϕθ⎡⎤⎢⎥⎣⎦⎰⎰,在立体角d Ω内找到粒子的概率是220(,,)r r dr d ψθϕ∞⎡⎤Ω⎢⎥⎣⎦⎰.(注:sin d d d θϕθΩ=) (二)态叠加原理:如果1ψ和2ψ是体系的可能状态,那么它们的线性叠加1122c c ψψψ=+(12c c 、为复数)也是这个体系可能的状态。
含义:当体系处于1ψ和2ψ的线性叠加态1122c c ψψψ=+(12c c 、为复数) 时,体系既处于1ψ态又处于态2ψ,对应的概率为21c 和22c .(三)概率密度(分布)函数2()()x x x ψωψ=若波函数为,则其概率密度函数为()(四)薛定谔方程:22()2i U r t m∂ψ=-∇ψ+ψ∂ 22222222222222222()21cos 1 ()sin sin x y zr r r r r θθθθθϕ∂∂∂∇=+∂∂∂⎛⎫∂∂∂∂∂∇=+++ ⎪∂∂∂∂∂⎝⎭拉普拉斯算符直角坐标球坐标问题:1.描写粒子(如电子)运动状态的波函数对粒子(如电子)的描述是统计性的.2. 薛定谔方程是量子力学的一个基本假设,不是通过严格的数学推导而来的(五)连续性方程:()**0( )2J tiJ mω∂+∇⋅=∂≡ψ∇ψ-ψ∇ψ注:问题:波函数的标准条件单值、连续、有界。