量子力学考博中用到的物理公式(复习时总结的)
- 格式:doc
- 大小:418.50 KB
- 文档页数:10

普朗克函数反函数普朗克函数 (Planck function) 是物理学中一个用于描述热辐射的函数,它由德国物理学家普朗克 (Max Planck) 创立。
普朗克函数的反函数也是物理学研究中的一个重要部分。
一、普朗克函数的定义普朗克函数是指一个与温度,波长和辐射强度相关的函数。
它通常用于描述黑体辐射过程中的能量分布和辐射强度的密度。
普朗克函数被广泛地应用于天体物理学、气象学、空间科学、核物理学等领域,因为它能帮助科学家们更好地理解和解释物质的热量特性。
二、普朗克函数的特性普朗克函数被定义为:$$B(\nu, T) =\frac{2h\nu^3}{c^2}\cdot\frac{1}{e^{\frac{h\nu}{k_bT}}-1}$$其中,$B(\nu, T)$ 表示在温度为 $T$ 的黑体内,频率为 $\nu$ 的辐射强度密度,$h$ 表示普朗克常数,$c$ 表示光速,$k_b$ 表示玻尔兹曼常数。
普朗克函数有以下几个特点:1. 频率越高,辐射强度密度越大。
2. 在短波长处,普朗克函数函数值急剧上升,而且在极短波长处,函数值趋近于无穷大。
3. 随着温度的升高,普朗克函数曲线向短波长方向移动,且曲线最大值也会向短波长方向移动。
三、普朗克函数反函数的意义普朗克函数反函数,也称为辐射定律,是指一个从辐射强度密度到温度之间的关系式。
它是普朗克函数的逆运算,意义重大。
普朗克函数反函数的求解可以帮助我们在物理学领域中解决很多实际的问题。
例如,它可以被用来计算太阳辐射的温度、判断天体运动的情况等等。
四、普朗克函数反函数的公式普朗克函数反函数字面上的意思是一个可以将辐射强度密度转化为温度的函数。
它可以用下面这个公式进行求解:$$T = \frac{h\nu}{k_b{ln(\frac{2h\nu^3}{Ic^2}+1)}}$$其中,$T$ 表示温度,$I$ 表示辐射强度密度,$\nu$ 表示频率,$h$ 表示普朗克常数,$c$ 表示光速,$k_b$ 表示玻尔兹曼常数。

上海市考研物理复习资料热学与量子统计物理重要公式总结热学是物理学中重要的分支之一,它研究了物质的热现象和能量转化规律。
量子统计物理则是热学的基础,研究了微观粒子的统计规律。
在考研物理的学习中,热学与量子统计物理是重要的内容,掌握相关的公式是非常关键的。
本文将为大家总结上海市考研物理复习资料中热学与量子统计物理的重要公式。
1. 热学公式总结1.1 热力学基本公式热力学基本公式包括内能变化、热量、功等的关系。
首先是内能变化公式:ΔU = Q - W其中,ΔU表示内能变化,Q表示系统吸收的热量,W表示系统对外界做的功。
热力学第一定律:ΔU = Q - W = Q - PΔV其中,P表示系统的压强,ΔV表示系统的体积变化。
热力学第二定律:ΔS ≥ 0其中,S表示系统的熵。
1.2 热力学循环公式在热力学中,循环过程是热力学研究的基本对象。
常见的热力学循环包括Carnot循环、Otto循环、Stirling循环等。
Carnot循环效率公式:η = 1 - T2/T1其中,η表示Carnot循环的效率,T2和T1分别表示低温和高温热源的温度。
Otto循环效率公式:η = 1 - (V3 - V2)/(V1 - V2)其中,η表示Otto循环的效率,V3、V2和V1分别表示活塞上下止点的体积。
1.3 热导公式热导是物质传导热量的能力,常用热导公式包括热导率、傅里叶热传导定律。
热导率公式:Q = kA(T2 - T1)/L其中,Q表示热量传递,k表示物质的热导率,A表示传热面积,L 表示传热距离,T2和T1分别表示传热的高低温。
傅里叶热传导定律:In = kA(ΔT/Δx)其中,In表示单位时间内传导热量,k表示物质的热导率,A表示传热面积,ΔT表示温度变化,Δx表示传热距离。
2. 量子统计物理公式总结2.1 量子力学基本公式量子力学基本公式包括波函数、算符和测量等的关系。
薛定谔方程:iħ∂Ψ/∂t = HΨ其中,i表示虚数单位,ħ表示约化普朗克常数,t表示时间,Ψ表示波函数,H表示哈密顿量。

量子力学公式
量子力学中的一些常见公式包括:
1. 薛定谔方程式:描述了量子物理学的宏观世界,即微观粒子如何随着时间的推移而演变。
其一般形式为:iℏ∂Ψ/∂t=HΨ,其中i是虚数单位,ℏ是普
朗克常数的约化常数,Ψ是波函数,H是哈密顿算符。
2. 波粒二象性:描述了物质粒子的波动性质和粒子性质之间的相互作用关系。
其表达式为λ=h/p,其中λ是波长,h是普朗克常数,p是粒子的动量。
3. 测量理论:物理量的测量和观测结果有一定的概率性和不确定性。
测量理论采用概率统计的方法来描述这种不确定性。
最常见的公式是海森堡不确定性原理:ΔxΔp≥h/4π,其中Δx和Δp分别表示位置和动量的不确定度,h 是普朗克常数。
4. 费米-狄拉克统计和玻色-爱因斯坦统计:描述了物质粒子的统计行为。
费米-狄拉克统计用于描述费米子(如电子、质子等)的行为,玻色-爱因斯坦统计用于描述玻色子(如光子、声子等)的行为。
5. 波函数的复共轭:Ψ^(r,t)。
6. 归一化条件:∫Ψ(r,t)^2d3r=1。
7. 位置算符:x。
8. 动量算符:-iℏ∇。
9. 能量算符:iℏ∂/∂t。
10. 完备性条件:∫ψn^(r)ψm(r)d3r=δnm。
以上公式仅供参考,如需更准确的信息,建议查阅量子力学相关的书籍或咨询专业人士。

量子物理公式总结量子物理是研究微观物质的行为规律的物理学分支,描述了微观世界的奇妙现象和量子系统的特性。
本文将对一些常见的量子物理公式进行总结和解释。
1. 波函数与薛定谔方程波函数是描述量子系统的数学工具,通常用符号ψ表示。
薛定谔方程是描述波函数演化随时间变化的定律。
薛定谔方程的一般形式为:iħ(∂ψ/∂t) = Hψ,其中i是虚数单位,ħ是约化普朗克常数,H是系统的哈密顿算符。
薛定谔方程是量子力学的基本方程之一,描述了波函数随时间的演化。
2. 波动性与粒子性的双重性质根据德布罗意假说,微观粒子也具有波动性。
德布罗意波长λ = h/p,其中h是普朗克常数,p是粒子的动量。
这个公式表明,质量较小的粒子具有更强的波动性。
3. 平面波的波函数平面波是一种纯粹的波动模式,其波函数可以表示为ψ(x) =Ae^(ikx),其中A是归一化系数,k是波矢,x是位置。
平面波的波函数具有连续的能量谱和动量谱。
4. 薛定谔方程的定态解薛定谔方程的定态解是指系统在某个特定能级上的解。
定态波函数可以用复数形式表示为ψ(x) = φ(x)e^(iEt/ħ),其中φ(x)是空间部分的波函数,E是能量。
定态解是量子力学中最基本的解,并用来描述电子在原子中的行为。
5. 测量与不确定原理根据不确定原理,无法同时精确测量粒子的位置和动量。
不确定原理的数学形式是ΔxΔp ≥ ħ/2,其中Δx是位置的不确定度,Δp是动量的不确定度,ħ是约化普朗克常数。
这意味着粒子的位置和动量无法同时完全确定,存在一定的不确定性。
6. 角动量算符与角动量量子化角动量算符描述了粒子的旋转运动特性,通常用符号L表示。
它是一个矢量算符,包括轨道角动量和自旋角动量。
角动量的量子化表明,角动量只能取一系列离散的值,即量子化。
7. 定态Schrödinger方程定态Schrödinger方程是薛定谔方程的简化形式,适用于定常态。
它可以写成Hψ = Eψ,其中H是系统的哈密顿算符,ψ是波函数,E是能量。



高三物理复习普朗克公式知识点
高三物理复习普朗克公式知识点
为了让考生在高考中取得更好的成绩,下面是店铺给大家带来的高三物理复习普朗克公式知识点,希望能帮到大家!
德国物理学家普朗克在量子论基础上建立的关于黑体辐射的正确公式。
19世纪末,经典统计物理学在研究黑体辐射时遇到了巨大的困难:由经典的能量均分定理导出的瑞利—金斯公式在短波方面得出同黑体辐射光谱实验结果相违背的.结论。
同时,维恩公式则仅适用于黑体辐射光谱能量分布的短波部分。
也就是说,当时还未能找到一个能够成功描述整个实验曲线的黑体辐射公式。
1900年普朗克获得一个和实验结果一致的纯粹经验公式,1901年他提出了能量量子化假设:辐射中心是带电的线性谐振子,它能够同周围的电磁场交换能量,谐振子的能量不连续,是一个量子能量的整数倍:[838—09]838—09式中是振子的振动频率,是普朗克常数,它是量子论中最基本的常数。
根据这个假设,可以导出普朗克公式:[838—01]838—01它给出辐射场能量密度,按频率的分布,式中是热力学温度,是玻耳兹曼常数。
如图表示辐射场能量密度随波长变化的曲线,它同实验结果完全一致。
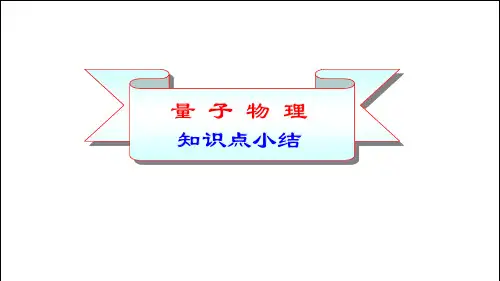
量子物理知识点小结一、普朗克能量子假说1、黑体辐射的实验定律2、普朗克能量子假说2)维恩位移定律:T λm = b1)斯特藩-玻耳兹曼定律: M (T ) = σT 4对频率为ν 的谐振子, 最小能量 ε 为: ⋅⋅⋅⋅⋅⋅,,,3,2,εεεεn νh =ε谐振子的能量不能取任意值,只能是某一最小能量ε 的整数倍,二、爱因斯坦光量子假说1、光量子假说 W m h νm+=221v 2、光电效应方程: 光具有“波粒二象性”光子的动量: λhp =光子的能量: h ν=ε碰撞过程中能量守恒: 2200mc h νc m h ν+=+v m e h e h n +=λλ00碰撞过程中动量守恒:波长的偏移量:)cos 1(0θλλλλ-=-=∆c nm 00243.0m 10432120=⨯⋅≈=-cm h c λ康普顿波长: 三、康普顿效应(X 射线光子与自由电子碰撞)四、玻尔氢原子理论一切实物粒子都具有波粒二象性 2)角动量量子化条件假设; 1)定态假设; 3)频率条件假设h νmc E ==2λh m p ==v ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥∆⋅∆≥∆⋅∆≥∆⋅∆222 z y x p z p y p x 2≥∆⋅∆t Ε五、德布罗意假说六、不确定性关系:七、波函数2、波函数满足的条件1、波函数的统计意义1)归一化条件t 时刻,粒子在空间r 处的单位体积中出现的概率, 与波函数模的平方成正比。
*2),(ΨΨt r ΨdVdW w === 概率密度: 12=⎰⎰⎰dV Ψ粒子在整个空间出现的总概率等于 1 , 即: 2)标准化条件:单值、连续、有限一维情况: 1)(2=⎰+∞∞-dx x Ψ八、定态薛定谔方程1、定态:若粒子的势能 E P (x ) 与 t 无关,仅是坐标的函数, 微观粒子在各处出现的概率与时间无关2、一维定态薛定谔方程: 0)()()(=-+x E E 2m dx x d P 222ψψ九、氢原子,3,2,1,1)8(22204=⋅-=n nh me E n ε1、能量量子化和主量子数n 2、角动量量子化和角量子数l)1(2)1(+=+=l l h l l L π1,,3,2,1,0-=n l 3、角动量空间量子化和磁量子数m ll m m L l l z ±±±==,,2,1,0, 4、自旋角动量和自旋量子数 21,)1(=+=s s s S 21,±==s s z m m S十、原子的电子壳层结构1、原子中电子状态由四个量子数(n 、l 、m l 、 m s )决定用 K , L , M , N , O , P , …. 表示 2、原子的壳层结构主量子数 n 相同的电子属于同一壳层壳层n = 1 , 2 , 3 , 4 , 5 , 6 , …. 同一壳层中( n 相同),l 相同的电子组成同一分壳层 支壳层 用 s , p , d , f , … , 表示l = 0, 1 , 2 , 3 , … , n -13、原子的壳层结构中电子的填充原则1) 泡利不相容原理2) 能量最小原理。
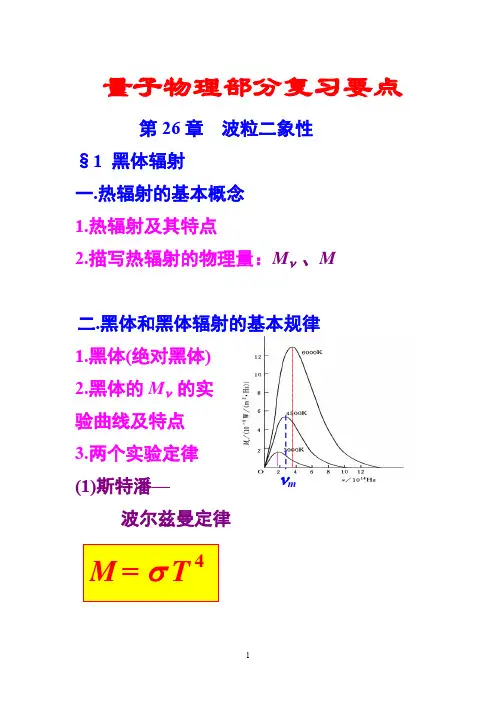
量子物理部分复习要点第26章波粒二象性§1 黑体辐射一.热辐射的基本概念1.热辐射及其特点2.描写热辐射的物理量:Mν、M二.黑体和黑体辐射的基本规律1.黑体(绝对黑体)2.黑体的Mν的实验曲线及特点3.两个实验定律νm(1)斯特潘—波尔兹曼定律(2)维恩位移定律四.普朗克的能量子假说和黑体辐射公式1.普朗克公式:2.普朗克假说§2.光电效应(自学)一.光电效应二.实验规律三.理论解释§3光的二象性光子一.爱因斯坦光子假说二.对光电效应的解释§4康普顿散射(Compton Scattering)一.康普顿散射及实验特点二.康普顿的理论解释1.物理图象2.会由能量守恒、动量守恒处理微观粒子的碰撞问题。
3.对康普顿效应的解释。
§5 粒子的波动性·德布罗意关系:会计算德布罗意波长(高速、低速)。
§6§7 不确定关系一.坐标和动量的不确定的关系二.时间与能量的不确定关系三.会用不确定关系作数量级估算和解释一些现象(如零点能的存在)第27章薛定谔方程一.薛定谔方程一维薛定谔方程一维薛定谔方程二.定态薛定谔方程一维定态薛定谔方程三.会用波函数的物理条件来解简单问题1.一维无限深方势阱的处理及结果2.一维势垒的穿透几率3 谐振子的结果第28章 原子、分子的能级与光谱 §1 氢原子的能级与光谱 一.玻尔的氢原子理论 二.量子力学的修正三.氢原子能级与光谱结果与图§2 碱金属原子的能级与光谱 一. 碱金属原子的能级与光谱特点及图主线系: 各 nP → 2S (最低S ) 第一辅线系:各 nD → 2P (最低P )sp df 4p 4d n Li 基态Li 原子H 原子(漫线系)第二辅线系:各 nS → 2P (最低P ),(n >2) (锐线系)基线系: 各 nF → 3D (最低D )二.角动量空间量子化(m l = l , l-1,……,-l+1 ,-l* μl z = -(e /2m )L z = -(e /2m ) m l h μl z = -m lμB玻尔磁子(是轨道磁矩的最小单元):ehμB = 2m三.电子自旋1.史特恩---盖拉赫实验(重要实验)2.电子自旋的假设 ·自旋角动量:自旋量子数s = 1/2 ·自旋在特殊方向的投影:自旋磁量子数:m s = ±(1/2)·自旋磁矩z B S★史特恩---盖拉赫实验的意义:(1)证实了空间量子化;(2)证实了自旋的存在。

量子力学公式期末总结量子力学公式在量子力学研究中起着关键的作用。
它们是以数学形式表达出量子力学中的物理定律,并为我们提供了一种理解微观世界的框架。
在期末总结中,我将讨论一些重要的量子力学公式,并说明它们在理论和实践中的应用。
首先,我们需要了解波函数(Ψ)的概念及其数学表述。
波函数可以描述量子系统在不同状态下的可能性分布。
在一维空间中,波函数可以表示为Ψ(x, t),其中x是位置,t是时间。
对于粒子在一维无势场中的运动,薛定谔方程描述了波函数的演化。
薛定谔方程是量子力学的基本方程之一,可以用以下形式表示:iħ∂Ψ/∂t = -ħ²/(2m) ∂²Ψ/∂x² + VΨ其中i是虚数单位,ħ是约化普朗克常数,m是粒子的质量,V是势能。
这个方程描述了波函数随时间和空间的演化。
解薛定谔方程可以得到粒子的能量和波函数。
下一个重要的概念是量子力学中的算符。
算符在量子力学中用于描述物理量的测量和演化。
一个重要的算符是哈密顿算符(H),它可以用于计算系统的总能量。
哈密顿算符可以表示为H = -ħ²/(2m) ∂²/∂x² + V(x)其中V(x)是势能。
求解薛定谔方程的本征问题,我们可以得到系统的能级和能量本征态。
量子力学中还有一些重要的定理和公式。
例如,海森堡不确定性原理表明,在同一时间内无法准确测量位置和动量。
这个原理可以用以下公式表示:ΔxΔp ≥ ħ/2其中Δx是位置的不确定度,Δp是动量的不确定度。
这个公式说明了位置和动量不可能同时完全确定的原理。
另一个重要的定理是保守量定理,也称为薛定谔定理。
根据这个定理,如果哈密顿算符与某个算符对易,那么这个算符就是系统的保守量。
这个定理可以用以下公式表示:[H, A] = 0其中[H, A]是哈密顿算符H和算符A的对易子。
根据薛定谔定理,我们可以得到一些守恒定律,例如动量守恒、角动量守恒等。
此外,我们还有其他一些重要的量子力学公式,例如- 波粒二象性关系:λ = h/p,其中λ是波长,h是普朗克常数,p是动量。

博士生物理学量子力学知识点归纳总结量子力学是现代物理学的重要分支,涉及到微观世界的粒子行为和物质性质的研究。
作为博士生物理学领域的学生,对于量子力学的掌握和理解至关重要。
本文将对博士生物理学中的一些重要的量子力学知识点进行归纳和总结,帮助读者更好地了解和学习量子力学。
一、波粒二象性量子力学最基本的概念之一就是波粒二象性。
根据波粒二象性原理,微观粒子既可以表现出粒子的粒状特性,又可以表现出波的波动特性。
这一概念对于解释诸如光的行为、物质的波动等现象起到了重要作用。
二、量子态与波函数在量子力学中,我们使用量子态和波函数来描述微观粒子的状态。
量子态是描述粒子的状态的数学概念,波函数则是量子态的数学表示。
波函数包含了粒子的位置、动量、自旋等信息。
通过对波函数的测量,我们可以了解粒子在不同态下的性质。
三、不确定性原理不确定性原理是量子力学中的一项重要原理,由海森堡提出。
该原理指出,在量子力学中,无法同时准确测量粒子的位置和动量,测量结果的精度有一个不可克服的限度。
这一原理限制了我们对粒子的准确观测。
四、量子力学算符算符在量子力学中起到了重要的作用,它们用于描述物理量的测量和量子系统的演化。
常见的量子力学算符包括哈密顿算符、动量算符、角动量算符等。
通过对这些算符的研究,我们可以得到量子系统的一些重要性质。
五、薛定谔方程薛定谔方程是量子力学的核心方程之一,描述了量子系统的时间演化。
它是一个包含波函数及其导数的偏微分方程,通过求解薛定谔方程,我们可以得到量子系统的波函数随时间的变化规律。
六、量子力学中的测量在量子力学中,测量是一个重要的概念。
与经典物理学中不同,量子力学中的测量是概率性的,通过测量可以得到一系列可能的结果。
测量结果的概率由波函数的模方给出,这被称为波函数坍缩。
七、量子力学中的叠加态与纠缠态量子力学中的叠加态和纠缠态是一些重要概念。
叠加态指的是量子系统处于多个可能状态的叠加状态,如双缝实验中的干涉现象。
物理学考研重要公式整理物理学考研是对学生物理学知识的全面检验,其中重要公式的掌握是取得好成绩的关键。
本文将为大家整理一些物理学考研中重要的公式,帮助大家更好地备考。
1.经典力学1.1.牛顿第二定律:F = ma这是经典力学中最重要的公式之一,描述了物体受到力的作用所产生的加速度。
1.2.万有引力公式:F = G * (m1m2 / r^2)该公式描述了两个物体之间的引力作用,其中G为万有引力常数,m1和m2分别为两个物体的质量,r为两个物体之间的距离。
1.3.动能定理:W = ΔK = (1/2)mv2 - (1/2)mu2动能定理描述了外力对物体所做的功等于物体动能的变化量,其中W为外力所做的功,ΔK为动能的变化量,m为物体的质量,v和u分别为物体的末速度和初速度。
2.电磁学2.1.库仑定律:F = k * (q1q2 / r^2)库仑定律描述了两个电荷之间的电力作用,其中k为库仑常数,q1和q2分别为两个电荷的电量,r为两个电荷之间的距离。
2.2.电场强度:E = F / q电场强度描述了单位正电荷所受到的电力大小,其中E为电场强度,F为电力,q为测试电荷。
2.3.电势能:U = qV电势能表示电荷在电场中具有的能量,其中U为电势能,q为电荷量,V为电势。
3.光学3.1.斯涅尔定律:n1sinθ1 = n2sinθ2斯涅尔定律描述了入射角、出射角和两介质折射率之间的关系,其中n1和n2分别为两个介质的折射率,θ1和θ2分别为入射角和出射角。
3.2.光的反射定律:θ1 = θ2光的反射定律描述了光线在平面镜等表面反射时入射角和反射角相等的关系,其中θ1为入射角,θ2为反射角。
3.3.光的干涉和衍射公式:dsinθ = mλ干涉和衍射公式描述了光的干涉和衍射现象中,入射光线与衍射屏幕上某一点的距离、衍射角和波长之间的关系,其中d为光程差,θ为衍射角,m为干涉和衍射的级次,λ为波长。
4.量子力学4.1.德布罗意波长:λ = h / p德布罗意波长描述了具有动量p的物体的波长,其中λ为德布罗意波长,h为普朗克常数。
量子力学常用计算公式1. 哈密顿算符(Hamiltonian Operator)哈密顿算符在量子力学中用于描述系统的总能量。
它的一般形式为:H = K + V其中,K表示动能算符,V表示势能算符。
2. 薛定谔方程(Schrödinger Equation)薛定谔方程是量子力学的基本方程,描述了量子系统的时间演化。
其一维形式为:iℏ∂ψ/∂t = -ℏ^2/(2m) ∂^2ψ/∂x^2 + Vψ其中,i表示虚数单位,ℏ为约化普朗克常数,m为粒子的质量,ψ为波函数,V为势能。
3. 波函数归一化(Normalization of Wavefunction)波函数必须满足归一化条件,即在整个空间积分后等于1。
对一维情况而言,归一化条件表示为:∫|ψ|^2 dx = 14. 物理量期望值(Expectation Value of Physical Quantity)物理量的期望值表示在量子态中对该物理量进行测量得到的平均值。
对一个可观测量A而言,其期望值定义为:<E[A]> = ∫ψ*Aψ dx其中,A表示物理量算符,ψ为波函数,*表示复共轭。
5. 不确定度原理(Uncertainty Principle)不确定度原理描述了同时测量一对共轭物理量(如位置和动量)的限制。
其数学表达为:ΔxΔp >= ℏ/2其中,Δx表示位置测量精度,Δp表示动量测量精度,ℏ为约化普朗克常数。
6. 一维势阱(One-dimensional Potential Well)一维势阱是一个常见的量子力学模型,用于探讨粒子在势能为零或有限的区域内的行为。
在无穷深势阱中,粒子的波函数为定态波函数,表示为:ψ_n(x) = sqrt(2/L) * sin(nπx/L)其中,L表示势阱的长度,n为正整数。
7. 自旋(Spin)自旋是粒子的固有属性,在量子力学中用于描述粒子的角动量。
自旋算符的本征态表示自旋的量子态,常用的自旋算符包括Sx、Sy和Sz。
上海市考研物理复习资料光学与量子力学重要公式总结在上海市考研物理复习过程中,光学与量子力学是必不可少的重要内容。
为了帮助考生更好地备考和复习,本文将总结光学与量子力学中的重要公式,供考生参考。
一、光学重要公式总结1. 光的波动性公式光速c = fλ,其中 c 为光速(约等于3×10^8 m/s),f 为光的频率,λ 为光的波长。
2. 平面波的复数表示A(x, t) = A0cos(kx-wt+φ),其中 A(x, t) 表示波动物理量 A 在位置 x 和时间 t 的值,A0 为振幅,k 为波数(k=2π/λ,λ 为波长),w 为角频率(w=2πf,f为频率),φ 为初相位。
3. 杨氏实验的干涉条件d*sinθ = mλ,其中 d 为狭缝间距,θ 为干涉条纹的角位置,m 为干涉条纹的级次,λ 为光的波长。
4. 薄透镜的公式光的折射定律:n1sinθ1 = n2sinθ2,其中 n1 和 n2 分别为光线入射介质和折射介质的折射率,θ1 和θ2 分别为入射角和折射角。
薄透镜的公式:1/f = (n-1)(1/R1-1/R2),其中 f 为透镜的焦距,n 为透镜的折射率,R1 和 R2 分别为透镜的两个曲率半径。
5. 双缝衍射的条件d*sinθ = mλ,其中 d 为缝宽,θ 为衍射条纹的角位置,m 为衍射条纹的级次,λ 为光的波长。
二、量子力学重要公式总结1. 德布罗意波长公式λ = h/p,其中λ 为物质波的波长,h 为普朗克常量(h≈ 6.63×10^(-34) J·s),p 为物质波的动量。
2. 薛定谔方程iħ(dψ/dt) = Hψ,其中 i 为虚数单位,ħ 为约化普朗克常量(ħ=h/2π),dψ/dt 为波函数ψ 对时间 t 的偏导数,H 为哈密顿算符。
3. 薛定谔方程的定态解ψ(x,t) = φ(x)e^(-iEt/ħ),其中ψ(x,t) 表示波函数,φ(x) 表示空间分布函数,E 表示能量。
上海市考研物理学专业复习资料量子力学重要公式推导量子力学是现代物理学的重要分支,它研究微观世界中的粒子行为。
在考研物理学专业的复习中,掌握量子力学的基本原理和重要公式是非常重要的。
本文将对量子力学中一些重要的公式进行推导,并为考生提供复习资料。
1. 波粒二象性量子力学中,粒子既具有粒子性又具有波动性。
这一概念由德布罗意提出,可以由以下公式表达:λ = h / p其中,λ表示粒子的波长,h为普朗克常数,p为粒子的动量。
2. 薛定谔方程薛定谔方程是量子力学的基础方程,可以描述粒子的行为。
对于自由粒子,薛定谔方程可以写作:Hψ = Eψ其中,H为哈密顿算符,ψ为波函数,E为能量。
3. 束缚态中的薛定谔方程对于束缚态中的粒子,薛定谔方程可以写作:Hψ = Eψ其中,H为哈密顿算符,ψ为波函数,E为能量。
对于一维势场中的束缚态问题,薛定谔方程可以简化为:-(h^2/2m)·(d^2ψ/dx^2) + V(x)ψ = Eψ其中,m为粒子的质量,V(x)为势场函数,E为能量。
4. 波函数归一化在量子力学中,波函数必须满足归一化条件,即积分值为1。
归一化条件的数学表达式为:∫|ψ|^2dx = 1其中,|ψ|^2为波函数的模方。
5. 算符与期望值在量子力学中,算符用于描述物理量的运算。
一个物理量对应一个算符,算符作用在波函数上可以得到该物理量的期望值。
算符的期望值计算公式为:< A > = ∫ψ*Aψdx其中,< A >表示物理量A的期望值,A为物理量对应的算符。
6. 不确定关系根据量子力学的原理,同时测量粒子的位置和动量是存在不确定性的。
不确定关系由下式表示:Δx·Δp >= h/2π其中,Δx表示位置的不确定度,Δp表示动量的不确定度,h为普朗克常数。
7. 角动量在量子力学中,角动量也是一个重要的物理量。
对于角动量,有以下重要公式:L = Iω其中,L为角动量,I为转动惯量,ω为角速度。
1、光子的能量和动量是:E=ℎ v=ћw、p=ℎvn/c=ℎn/λ=ћk2、量子现象:由以上两个公式可以看出,在宏观现象中,h和其他物理量相比较可以略去,因而辐射的能量可以连续变化,因此凡是h在其中起重要作用的现象都可以称为量子现象。
3、量子化条件:在量子理论中,角动量必须是h的整数倍4、量子化条件的推广:∮pdq=(n+1/2)ℎ, n是0和正整数,称为量子数。
5、德布罗意公式:E=ℎv=ћw、p=ℎ/λn=ћk6、波函数的统计解释:波函数在空间中某一点的强度(振幅绝对值的平方)和在该点找到粒子的概率成比例。
dw(x,y,z,t)= C∣Φ(x,y,z,t)∣²dτ7、态叠加原理:对于一般的情况,如果Ψ1和Ψ2是体系的可能状态,那么它们的线性叠加Ψ=c1Ψ1+c2Ψ2(c1,c2是复数),也是这个体系的一个可能状态,这就是量子力学中的态叠加原理。
态叠加原理还有一个含义:当粒子处于态Ψ1和态Ψ2的线性叠加态Ψ时,粒子时既处在态Ψ1又处在态Ψ2.注意:态叠加原理指的是波函数(概率幅)的线性叠加,而不是概率的叠加8、波函数的标准条件:有限性、连续性、导致可测量的单值性9、什么是定态定态:体系处于Ψ(r,t)=ψ(r)e~-iEt/ћ所描写的状态时,能量具有确定性,这种状态称为定态。
Ψ(r,t)=ψ(r)e~-iEt/ћ称为定态波函数10、定态薛定谔方程:−ћ²/2m▽²ψ+U(r)ψ=Eψ11、本征值方程:ĤΨ=EΨ,E称为算符Ĥ的本征值,Ψ称为算符Ĥ属于本征值E的本征函数12、薛定谔波动方程的一般解可以写为这些定态波函数的线性叠加:13、束缚态:通常把在无限远处为零的波函数所描写的状态称为束缚态14、隧道效应:粒子在能量E小于势垒高度时仍能贯穿势垒的现象15、厄米算符:量子力学中表示力学量的算符都是厄米算符。
算符F̂满足下列等式:∫ψ∗F̂φdx=∫(F̂ψ)∗φdx16、力学量与算符的关系的一个基本假设:量子力学中,表示力学量的算符都是厄米算符,它们的本征函数组成完全系当体系处于波函数ψ(x)所描写的状态时,测量力学F所得的数值,必定是算符F^的本征值之一,测得λn的概率是|Cn∣²17、对易与不对易的关系:如果两个算符F̂和Ĝ,有一组共同本征函数φn而且φn组成完全系,则算符F̂和Ĝ对易。
量子力学常用积分公式 (1)dx e x an e x a dx e x axn ax n axn ⎰⎰--=11 )0(>n (2) )cos sin (sin 22bx b bx a ba e bxdx e axax-+=⎰ (3) =⎰axdx e axcos )sin cos (22bx b bx a ba e ax++ (4)ax x a ax aaxdx x cos 1sin 1sin 2-=⎰ (5) =⎰axdx x sin 2ax a xaax a x cos )2(sin 2222-+ (6)ax a xax a axdx x sin cos 1cos 2+=⎰(7ax a a x ax ax axdx x sin )2(cos 2cos 3222-+=⎰))ln(2222c ax x a ac c ax x ++++ (0>a ) (8)⎰=+dx c ax 2)arcsin(222x c a ac c ax x --++ (a<0) ⎰20sin πxdx n2!!!)!1(πn n - (=n 正偶数)(9) =⎰20cos πxdx n!!!)!1(n n - (=n 正奇数) 2π(0>a ) (10)⎰∞=0sin dx xax2π- (0<a ) (11))1!+∞-=⎰n n ax a n dx x e (0,>=a n 正整数) (12)adx e ax π2102=⎰∞-(13) 121022!)!12(2++∞--=⎰n n ax n a n dx e x π(14)1122!2+∞-+=⎰n ax n an dx e x (15)2sin 022adx xax π⎰∞= (16)⎰∞-+=222)(2sin b a abbxdx xe ax (0>a )⎰∞-+-=022222)(c o s b a b a b x d x xeax(0>a )第二章:函数与波动方程[1] 试用量子化条件,求谐振子的能量[谐振子势能2221)(x m x V ω=] (解)(甲法)可以用Wilson-Sommerfeld 的量子化条件式:⎰=nh pdq在量子化条件中,令⋅=x m p 为振子动量,x q = 为振子坐标,设总能量E则 22222x m m P E ω+= )2(222x m E m p ω-=代入公式得:nh dx x m E m =-⎰)2(222ω量子化条件的积分指一个周期内的位移,可看作振幅OA 的四倍,要决定振幅a ,注意在A 或B 点动能为0,2221a m E ω=,(1)改写为:nh dx x a m aa=-⎰-222ω (2)积分得:nh a m =πω2遍乘πω21得 ωπω n h E ==2[乙法]也是利用量子化条件,大积分变量用时间t 而不用位移x ,按题意振动角频率为ω,直接写出位移x ,用t 的项表示:t a x q ωsin ==求微分:tdt a dx dq ωωcos == (4) 求积分:t ma x m p ωωcos ==⋅(5) 将(4)(5)代量子化条件:nh tdt ma pdq T==⎰⎰0222cos ωω T 是振动周期,T=ωπ2,求出积分,得nh a m =πω2 ωπωn n h E ==2 3,2,1=n 正整数 #[2]用量子化条件,求限制在箱内运动的粒子的能量,箱的长宽高分别为.,,c b a(解)三维问题,有三个独立量子化条件,可设想粒子有三个分运动,每一分运动是自由运动.设粒子与器壁作弹性碰撞,则每碰一次时,与此壁正交方向的分动量变号(如ppxx-→),其余分动量不变,设想粒子从某一分运动完成一个周期,此周期中动量与位移同时变号,量子化条件:pp n q p xax xxxa dx h d 220===⎰⎰ (1) pp n q pyby y y ybdy h d 22===⎰⎰ (2)pp n q p zcz z z zc dz hd 22===⎰⎰(3)pp p zyx,,都是常数,总动量平方222z y x p p p p ++=总能量是:)(2122222z y x p p p mm p E ++===])2()2()2[(21222ch b h a h m n n n z y x ++ =])()()[(82222cb a m h n n n z y x ++ 但3,2,1,,=n n n z y x 正整数.#[3] 平面转子的转动惯量为I ,求能量允许值.(解)解释题意:平面转子是个转动体,它的位置由一坐标(例如转角ϕ)决定,它的运动是一种刚体的平面平行运动.例如双原子分子的旋转.按刚体力学,转子的角动量I ω,但⋅=ϕω是角速度,能量是221ωI =E 利用量子化条件,将p 理解成为角动量,q 理解成转角ϕ,一个周期内的运动理解成旋转一周,则有nh d pdq =I =I =⎰⎰ωπϕωπ220(1)(1) 说明ω是量子化的(2)I=I =n nh πω2 (3,2,1=n ……..) (2) (3) 代入能量公式,得能量量子化公式:I=I I =I =2)(2212222 n n E ω (3)#[4]有一带电荷e 质量m 的粒子在平面内运动,垂直于平面方向磁场是B,求粒子能量允许值.(解)带电粒子在匀强磁场中作匀速圆周运动,设圆半径是r ,线速度是v ,用高斯制单位,洛伦兹与向心力平衡条件是:rmv c Bev 2= (1) 又利用量子化条件,令=p 电荷角动量 =q 转角ϕnh mrv mrvd pdq ===⎰⎰πϕπ220(2)即 nh mrv = (3) 由(1)(2)求得电荷动能=mcnBe mv 2212 =再求运动电荷在磁场中的磁势能,按电磁学通电导体在磁场中的势能=c B r ev c c *****2π==场强线圈面积电流场强磁矩,v 是电荷的旋转频率, rvv π2=,代入前式得运动电荷的磁势能=mcnBe 2 (符号是正的) 点电荷的总能量=动能+磁势能=E=mcnBe 2 ( 3,2,1=n )#[5]对高速运动的粒子(静质量m )的能量和动量由下式给出:2221c v mc E -=(1)2221c v mv p -=(2)试根据哈密顿量 2242p c c m E H +== (3)及正则方程式来检验以上二式.由此得出粒子速度和德布罗意的群速度相等的关系.计算速度并证明它大于光速.(解)根据(3)式来组成哈氏正则方程式组:pqiiH ∂∂=⋅,本题中v q i=⋅,p pi=,因而224222242pc c m p c p c c m pv +=+∂∂= (4)从前式解出p (用v 表示)即得到(2).又若将(2)代入(3),就可得到(1)式. 其次求粒子速度v 和它的物质波的群速度vG间的关系.运用德氏的假设: k p =于(3)式右方, 又用ω =E 于(3)式左方,遍除h :)(22242k k c c m ωω=+=按照波包理论,波包群速度vG是角频率丢波数的一阶导数:22242k c c m kv G +∂∂= =22422222422pc c m p c k c c m kc +=+最后一式按照(4)式等于粒子速度v ,因而v vG=。
初等量子力学的四块容一、薛氏方程C1:波函数与薛氏方程 1、付氏变换:(动量→坐标为正)/3321()()(2)i p r r p e d p ψψπ+∞⋅-∞=⎰2、δ函数的两个重要极限及一个积分公式1()2i x x e d αδαπ∞-∞=⎰(相当于物理中的波粒转换)其推导过程:000()0()()()1()()2i x x f x f x x x dxf x dxd f xe αδαπ∞-∞∞∞--∞-∞=-=⎰⎰⎰两式比较得出。
24()lim i i xx eπααδ-=(试题1.5用到)24i i e d ξπξ∞-∞=⎰(好像与某个积分是一样的,只是有些变换)3、证明技巧等式一边含有V ,而一边没有。
222V m⇒-∇+肯定是作为一个整体消去的。
4、波函数平方可积的要求23(3/2),()s d r A r r r ψψ-+=⇒→∞⎰全(0s >) 可以在证明某些概率守恒的式子时(体积分→面积分VSAdV A ds ∇⋅=⋅⎰⎰),可以得到一些式子的积分为0。
5、(,0)(,)x x t ψψ→先将(,0)x ψ展为能量本征态的线性组合(自由粒子时即可以通过付氏化为()p ψ),再/(,)()iEt E n x t C x e ψψ-=∑。
C2:一维势场中的粒子 1、各种势类型方势、δ势、谐振子、半壁无限谐振子(谐振子奇数解)、半壁无限方势、不对称方势阱。
2、()()((),())n n n n nx C x C x x ψϕϕψ=⇒=∑。
*()()n n C x x dx ϕψ=⎰(注意积分围)221122222221122H C E C E H C E C E =+=+3、无限深势阱的解)()0n n x x a πψ=⎩。
22222n n E ma π=(能量可通过22222P E m m -∇==求得)4、谐振子的解2212()(!)()n x n n x n eH x αψα-=⋅其中α=。
5、递推关系12()2()2()0n n n H x xH x nH x ----=1()2()n n H x nH x -'=()(1)()n n n x x ψψ-=-(所以对于半壁无限高的谐振子只有奇数才可以满足)C5:中心力场 1、径向波函数()()R r r r χ=22(1)()[(())]()02l l l l r E V r r rχχμ+''⇒+--=0r →时,若有20lim ()0r r V r →=,则()l l R r r 。
2、无限深球方势阱○1S 态(0l =),其与无限深方势阱一样。
○20l ≠时,令kr ρ= 则本征方程222(1)()()[]()00()0l l l l l l R r R r k R r r ar r R a boundry condition+⎧'''++-=≤≤⎪⎨⎪=-⎩转化为球Bessel 方程。
()()l l R r j kr ,从()0l j ka =导出能量本征值。
3、三维各向同性谐振子(合流超几何函数)3()22N r E N N n l ω=+=+简并度:1(1)(2)2n f N N =++,若计及电子自旋时,则2⨯。
F-H 定理:对l 求导,可得出21r,对ω求导,可得出2r 。
球坐标↔直角坐标01110001101001000100001ψψψ-⎡⎤--Φ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-Φ⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥Φ⎣⎦⎣⎦⎢⎥⎣⎦(相当于在三、四象限)4、氢原子(合流超几何函数)22112N r e E n n l a n =-=++,其中22a eμ=(Bohr 半径)。
简并度:2n f n =,若计及电子自旋时,则2⨯。
F-H 定理:对l 求导,可得出21r。
位力定理可得出类氢原子1r,2p ,在计算过程要注意电荷量Z 。
基氢波函数:1/10031()r ae aψπ-=。
5、圆轨道(0,1rn n l ==+)最概然半径:20,1()0n dr drχ-≡0/0,1()Zr na n n r Cr e χ--⇒=。
20/n r n a Z =。
6、二维不对称谐振子222211(,)22x y V x y x y ωω=+,在计算简并度,把N 表示成,x y n n 的表达式。
7、二维Coulomb 势C9:力学本征值的代数解法二、算符理论C3:力学量用算符表示 1、厄米算符(,)(,)A A ψϕψϕ=(即可以把算符写在任意函数前)22(,)(,)0A A A A ψψψψ⇒==≥2、不确定公式[][]1/2,1/2,A B A B A B ∆⋅∆≥∆∆=(不确定度与对易平均值有关)3、球谐函数(1)(cos )mmim lm l Y e ϕθ=- 4、箱归一化 若要ix∂-∂为厄米算符,⇒周期条件:()()22L L ψψ-=。
5、B —K (Baker-Hausdorff )公式(通过定义函数来证明)[]1212(,)A B A B C B A Ce e e e e e e A B C +-===6、在计算某个算符的平均值时,可以通过对易关系化为算其它算符的平均值。
2,[,],2p p imr H r i p r H m m -⎡⎤⎡⎤==⇒=⎣⎦⎣⎦ ,z x y l i l l ⎡⎤=⎣⎦。
C4:力学量随时间变化与对称性1、三个定理○1位力定理(定态时成立,即能量本征态,由,0di r p r p H dt⎡⎤⋅=⋅=⎣⎦导出)212p r V T r V m=⋅∇⇒=⋅∇ ○2Ehrenfest 定理(newton law ) 22()d m r F r dt=由下面两个式子导出 1,1,()()d pr r H dt i m d pp H V r F r dt i⎡⎤==⎣⎦⎡⎤==-∇⋅=⎣⎦ ○3F-H (Feynman-Hellmann )定理 n n n E H ψψλλ∂∂=∂∂(证明题中右矢与左矢的对应运用) 2、守恒量[]1(),d A t A H A dt i t∂=+∂ 3、Heisenberg 图像(给算符加一个时间算符)//()(,0)(0)(,0)(0)iH t iH t A t U t A U t e A e +-==导出Heisenberg 方程[]1()(),d A t A t H dt i=。
(可以解算符随时间的变化情况)。
4、全同粒子(交换算符)Fermi 子不能有两个粒子处于同一个态。
把粒子能待的态选好后,由于对称性要求Bose 子和Fermi 子都只有一种波函数,关键在于选好粒子处于哪些态。
三、矩阵力学C7:量子力学的矩阵形式与表象变换 四、相互作用C6:电磁场中粒子的运动(电子与磁场作用)1、H 量21()2qA H P q C φμ=-+1B A E A C t φ⎧=∇⨯⎪⎨∂=--∇⎪∂⎩本征方程:22221[]22q q i p A P A q t C Cψφψμμμ∂=-⋅++∂,比无作用时多出二项。
(其中利用了0A ∇⋅=)2、正常Zeeman 效应(氢原子+z l 作用项)恒磁场沿Z 方向,取相应的矢势12A B r =⨯。
11,,022x y z A By A Bx A ⇒=-==2222221[()]()24z eB e B H p l x y V r C Cμ⇒=++++ 比氢原子多出两项,z l 作用项,反磁项。
(在原子中反磁项太小可忽略) 能量本征态(与氢原子一样),取2(,,)z H ll 的本征态。
能级:r r n lm n l L E E m ω=+。
定义电子轨道磁矩:2z z el Cμμ=-,Larmor 频率2L eB C ωμ=。
3、Laudau 能级(两维对称谐振子+z l 作用项+一维自由粒子)两维对称谐振子:222222021[()]24x y e B H p p x y Cμ=+++。
z l 作用项:112z eBH l Cμ=。
一维自由粒子:2212z H p μ=。
4、电场与磁场垂直:(,0,0),(0,0,)B B εε==,则可取,(0,,0)x A Bx φε=-=。
C8:自旋(四维空间)1、Pauli 算符三性对易关系、归一性、厄米性σσ+=。
⇒双Pauli 算符的关系(诸如:x y z i σσσ=),所以任意级数都可以表示成线性形式(如可令:0123z z i i x x y z e e C I C C C λσλσσσσσ-=+++),单独线性算符的迹为0。
2、总角动量的本征态(22(,,,)z H lj j )自旋轨道作用项:2211()2dVr s l s l C r drξμ⋅=⋅。
先假定:1(,,)lm z lm aY s bY φθϕ+⎛⎫= ⎪⎝⎭推导过程为:2l l ⇒(相同),,1z j m m ⇒+(相差为1,是因为自旋的原因),2,j a b ⇒(推导出两者系数之间的关系)利用关系式222324j l s l =++⋅,计算在能量本征态下s l ⋅的平均值。
综上:○11/2j l =+1lm ljmlm φ+⎤=⎥⎢⎥⎣⎦○21/2(0)j l l =-≠ 1lm ljmlm φ+⎡⎤=⎥⎥⎦○30l =(无轨道角动量) 001111000022220,0Y Y φφ-⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦3、光普双线结构(径向方程不同,导致能级分裂) ○11/2j l =+ 2[()]()()2lA r R r ER r ξ+=○21/2(0)j l l =-≠ 2(1)[()]()()2l A r R r ER r ξ+-=4、反常Zeeman反常Zeeman=自旋轨道作用+正常Zeeman即(eg:p 态)1/2(21)1/2j l l j m j l +⎛⎫→→+ ⎪-⎝⎭选择定则:1,0,1,0, 1.j l j m ∆=±∆=±∆=±5、单态(波函数对称为Fermi 子)与三态(波函数对称为Bose 子) 就是讨论双电子轨道杂化212(,)(,)z s s SS ↔的转换。
6、一些总结在某态下求算符的可能测值,必须先给出算符的所有本征态,再波函数按本征态展开。
在求某态随时间变化时,必须给出H 量的本征态与能级。
在找角动量的守恒集时,H 量含角动量的交叉项(12s s ⋅),首选2(,)z S S 的共同本征函数。
C10:微扰论 1、束缚态(1)(0)(0)(2)(1)(0)(3)(2)(0)E H E H E H ψψψψψψ⎧'=⎪⎪'=⎨⎪'=⎪⎩(3)(1)(1)(1)E H E ψψ'=-○1非简并一级近似:(1)(1)(0)n n na ψψ=∑(1)kkkE H '⇒=,(1)(0)(0)(0)'nk nnk n H E E ψψ'=-∑。