山西山大附中2015-2016学年高一上学期10月月考数学试卷 Word版含解析

2015-2016学年山西山大附中高一（上）10月月考数学试卷一．选择题（本大题共12小题，每小题3分，共36分）1．已知集合U={1，3，5，7，9}，A={1，5，7}，则∁U A=( )A．{1，3} B．{3，7，9} C．{3，5，9} D．{3，9}2．如果A={x|x＞﹣1}，那么( )A．0⊆A B．{0}∈A C．∅∈A D．{0}⊆A3．已知集合A={（x，y）|y=x2}，B={（x，y）|y=x}，则A∩B=( )A．{0，1} B．{（0，0），（1，1）} C．{1} D．{（1，1）}4．在映射f：A→B中，A=B={（x，y）|x，y∈R}，且f：（x，y）→（x﹣y，x+y），则与A中的元素（﹣1，2）对应的B中的元素为( )A．（﹣3，1）B．（1，3）C．（﹣1，﹣3）D．（3，1）5．已知全集U=R，A={x|x＜1}，B={x|x≥2}，则集合∁U（A∪B）=( )A．{x|1≤x＜2} B．{x|1＜x≤2}C．{x|x≥1} D．{x|x≤2}6．下列各图中，可表示函数y=f（x）的图象的只可能是( )A．B．C．D．7．已知全集U=R，集合A={x|＜0}，B={x|x≥1}，则集合{x|x≤0}等于( )A．A∩B B．A∪B C．∁U（A∩B）D．∁U（A∪B）8．已知f（x）=，则f（﹣3）为 ( )A．2 B．3 C．4 D．59．已知集合A={x|x=3n+2，n∈N}，B={6，8，10，12，14}，则集合A∩B中的子集个数为( ) A．2 B．4 C．8 D．1610．若函数y=f（x）的定义域是[0，2]，则函数的定义域是( ) A．[0，1] B．[0，1）C．[0，1）∪（1，4] D．（0，1）11．下面给出四个论断：①{0}是空集；②若a∈N，则﹣a∉N；③集合A={x∈R|x2﹣2x+1=0}有两个元素；④集合是有限集．其中正确的个数为( )A．0 B．1 C．2 D．312．已知f（x）=，则不等式xf（x）+x≤2的解集为( )A．[0，1] B．[0，2] C．（﹣∞，2] D．（﹣∞，1]二．填空题（本大题共4小题，每小题4分，共16分.）13．已知函数的定义域为__________．14．已知全集U={1，2，3，4，5，6，7，8}，（∁U A）∩B={1，3，4}，（∁U A）∩（∁U B）={5，7}，A∩B={2}，则集合A=__________．15．设全集U={2，3，a2+2a﹣3}，A={|2a﹣1|，2}，∁U A={5}，则a=__________．16．函数f（x）=的定义域为[﹣2，1]，则a的值为__________．三．解答题（本大题共5小题，共48分.解答应写出必要的文字说明）17．已知函数f（x）的图象如图所示．（1）求函数f（x）的解析式；（2）求函数f（x）的定义域和值域．18．解下列不等式：（1）（2）|x﹣1|+|2x﹣1|＜3．19．已知集合A={x||x﹣1|＜2}，，U=R，求A∩B，A∪B，A∩（C U B）．20．已知函数f（x）=的定义域为集合A，函数g（x）=x2﹣2x+a，x∈[0，4]的值域为集合B，若A∪B=R，求实数a的取值范围．21．已知集合A={x|x2﹣3x+2=0}，B={x|x2+2（a+1）x+（a2﹣5）=0}，（Ⅰ）若B={2}，求实数a的值；（Ⅱ）若A∪B=A，求实数a的取值范围．2015-2016学年山西山大附中高一（上）10月月考数学试卷一．选择题（本大题共12小题，每小题3分，共36分）1．已知集合U={1，3，5，7，9}，A={1，5，7}，则∁U A=( )A．{1，3} B．{3，7，9} C．{3，5，9} D．{3，9}【考点】补集及其运算．【分析】从U中去掉A中的元素就可．【解答】解：从全集U中，去掉1，5，7，剩下的元素构成C U A．故选D．【点评】集合补集就是从全集中去掉集合本身含有的元素后所构成的集合．2．如果A={x|x＞﹣1}，那么( )A．0⊆A B．{0}∈A C．∅∈A D．{0}⊆A【考点】集合的包含关系判断及应用．【专题】探究型．【分析】利用元素和集合A的关系，以及集合Φ，{0}中元素与集合A的元素关系进行判断．【解答】解：A.0为元素，而A={x|x＞﹣1}，为集合，元素与集合应为属于关系，∴A错误．B．{0}为集合，集合和集合之间应是包含关系，∴B错误．C．∅为集合，集合和集合之间应是包含关系，∴C错误．D．{0}为集合，且0∈A，∴{0}⊆A成立．故选D．【点评】本题考查了元素和集合以及集合与集合之间的关系．元素与集合之间应使用“∈，∉”，而集合和集合之间应使用包含号．3．已知集合A={（x，y）|y=x2}，B={（x，y）|y=x}，则A∩B=( )A．{0，1} B．{（0，0），（1，1）} C． {1} D．{（1，1）}【考点】交集及其运算．【专题】计算题；集合思想；集合．【分析】联立A与B中两方程组成方程组，求出方程组的解即可确定出A与B的交集．【解答】解：联立A与B中的方程得：，消去y得：x2=x，即x（x﹣1）=0，解得：x=0或x=1，把x=0代入得：y=0；把x=1代入得：y=1，∴方程组的解为，，则A∩B={（0，0），（1，1）}，故选：B．【点评】此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．4．在映射f：A→B中，A=B={（x，y）|x，y∈R}，且f：（x，y）→（x﹣y，x+y），则与A中的元素（﹣1，2）对应的B中的元素为( )A．（﹣3，1）B．（1，3）C．（﹣1，﹣3）D．（3，1）【考点】映射．【专题】计算题．【分析】根据已知中映射f：A→B的对应法则，f：（x，y）→（x﹣y，x+y），将A中元素（﹣1，2）代入对应法则，即可得到答案．【解答】解：由映射的对应法则f：（x，y）→（x﹣y，x+y），故A中元素（﹣1，2）在B中对应的元素为（﹣1﹣2，﹣1+2）即（﹣3，1）故选A【点评】本题考查的知识点是映射的概念，属基础题型，熟练掌握映射的定义，是解答本题的关键．5．已知全集U=R，A={x|x＜1}，B={x|x≥2}，则集合∁U（A∪B）=( )A．{x|1≤x＜2} B．{x|1＜x≤2}C．{x|x≥1} D．{x|x≤2}【考点】交、并、补集的混合运算．【专题】集合．【分析】求出A与B的并集，根据全集U=R，求出并集的补集即可．【解答】解：∵全集U=R，A={x|x＜1}，B={x|x≥2}，∴A∪B={x|x＜1或x≥2}，则∁U（A∪B）={x|1≤x＜2}，故选：A．【点评】此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．6．下列各图中，可表示函数y=f（x）的图象的只可能是( )A．B．C．D．【考点】函数的概念及其构成要素．【专题】函数思想；定义法；函数的性质及应用．【分析】根据函数的定义进行判断即可．【解答】解：A．图象中存在，一个x有两个y值与x对应，不满足函数对应的唯一性，不是函数图象．B．图象中存在，一个x有两个y值与x对应，不满足函数对应的唯一性，不是函数图象．C．图象中存在，一个x有两个y值与x对应，不满足函数对应的唯一性，不是函数图象．D．图象中满足函数对应的唯一性，是函数图象．故选：D．【点评】本题主要考查函数图象的判断，利用函数的定义是解决本题的关键．7．已知全集U=R，集合A={x|＜0}，B={x|x≥1}，则集合{x|x≤0}等于( )A．A∩B B．A∪B C．∁U（A∩B）D．∁U（A∪B）【考点】交、并、补集的混合运算．【专题】计算题．【分析】先解分式不等式化简集合A，求出集合A与集合B的并集，观察得到集合{x|x≤0}是集合（A∪B）在实数集中的补集．【解答】解：由，得x（x﹣1）＜0，解得：0＜x＜1．所以A={x|＜0}={x|0＜x＜1}，又B={x|x≥1}，则A∪B={x|0＜x＜1}∪{x|x≥1}={x|x＞0}，所以，集合{x|x≤0}=C U（A∪B）．故选D．【点评】本题考查了分式不等式的解法，求解分式不等式时，可以转化为不等式组或整式不等式求解，考查了交、并、补集的混合运算．此题是基础题．8．已知f（x）=，则f（﹣3）为 ( )A．2 B．3 C．4 D．5【考点】函数的值；分段函数的应用．【专题】函数的性质及应用．【分析】根据已知中f（x）=，将x=﹣3代入递推可得答案．【解答】解：∵f（x）=，∴f（﹣3）=f（﹣1）=f（1）=f（3）=f（5）=f（7）=7﹣5=2，故选：A．【点评】本题考查的知识点是分段函数的应用，函数的值，难度不大，属于基础题．9．已知集合A={x|x=3n+2，n∈N}，B={6，8，10，12，14}，则集合A∩B中的子集个数为( ) A．2 B．4 C．8 D．16【考点】交集及其运算．【专题】集合．【分析】由A与B，求出两集合的交集，找出交集的子集个数即可．【解答】解：∵A={x|x=3n+2，n∈N}，B={6，8，10，12，14}，∴A∩B={8，14}，则集合A∩B中的子集个数为22=4，故选：B．【点评】此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．10．若函数y=f（x）的定义域是[0，2]，则函数的定义域是( )A．[0，1] B．[0，1）C．[0，1）∪（1，4] D．（0，1）【考点】函数的定义域及其求法．【分析】根据f（2x）中的2x和f（x）中的x的取值范围一样得到：0≤2x≤2，又分式中分母不能是0，即：x﹣1≠0，解出x的取值范围，得到答案．【解答】解：因为f（x）的定义域为[0，2]，所以对g（x），0≤2x≤2且x≠1，故x∈[0，1），故选B．【点评】本题考查求复合函数的定义域问题．11．下面给出四个论断：①{0}是空集；②若a∈N，则﹣a∉N；③集合A={x∈R|x2﹣2x+1=0}有两个元素；④集合是有限集．其中正确的个数为( )A．0 B．1 C．2 D．3【考点】集合的包含关系判断及应用；元素与集合关系的判断．【专题】计算题；集合．【分析】对四个选项分别进行判断，即可得出结论．【解答】解：：①{0}中有元素0，不是空集，不正确；②若a∈N，则﹣a∉N，不正确；③集合A={x∈R|x2﹣2x+1=0}有1个元素1，不正确；④集合是无限集，不正确．故选：A．【点评】本题借助考查命题的真假判断，考查了自然数集的表示及集合中元素的性质，集合中元素性质：无序性、确定性、互异性．12．已知f（x）=，则不等式xf（x）+x≤2的解集为( )A．[0，1] B．[0，2] C．（﹣∞，2] D．（﹣∞，1]【考点】其他不等式的解法．【专题】不等式的解法及应用．【分析】分类讨论，分x≥0、x＜0时解答，最后求并集即可．【解答】解：x≥0时，f（x）=1，不等式xf（x）+x≤2可化为2x≤2解得x≤1，∴0≤x≤1；当x＜0时，f（x）=0，不等式xf（x）+x≤2可化为x≤2，∴x＜0．综上可得x≤1．故选：D【点评】本题考查分类讨论法解不等式，属基础题．二．填空题（本大题共4小题，每小题4分，共16分.）13．已知函数的定义域为{x|x≥﹣2且x≠0}．【考点】函数的定义域及其求法．【专题】转化思想；定义法；函数的性质及应用．【分析】根据函数成立的条件即可求函数的定义域．【解答】解：要使函数有意义，则，即，则x≥﹣2且x≠0，故函数的定义域为{x|x≥﹣2且x≠0}，故答案为：{x|x≥﹣2且x≠0}【点评】本题主要考查函数定义域的求解，根据函数成立的条件建立不等式关系是解决本题的关键．14．已知全集U={1，2，3，4，5，6，7，8}，（∁U A）∩B={1，3，4}，（∁U A）∩（∁U B）={5，7}，A∩B={2}，则集合A={2，6，8}．【考点】交、并、补集的混合运算．【专题】集合思想；转化法；集合．【分析】根据集合之间的基本运算关系，求出集合B，即可求出∁U A与A．【解答】解：∵全集U={1，2，3，4，5，6，7，8}，（∁U A）∩B={1，3，4}，∴{1，3，4}⊆B，且{1，3，4}⊆（∁U A）；∵（∁U A）∩（∁U B）={5，7}，∴{5，7}⊆∁U A，且{5，7}⊆∁U B；又A∩B={2}，∴{2}⊆A，且{2}⊆B；∴B={1，2，3，4}；∴∁U A={1，3，4，5，7}；∴A={2，6，8}．故答案为：{2，6，8}．【点评】本题考查了交集、并集、补集的概念与运算问题，是基础题目．15．设全集U={2，3，a2+2a﹣3}，A={|2a﹣1|，2}，∁U A={5}，则a=2．【考点】子集与交集、并集运算的转换．【专题】计算题．【分析】由题意得 5在全集中，故a2+2a﹣3=5，|2a﹣1|在全集中，且不是2和5，故|2a﹣1|=3．【解答】解：由题意得|2a﹣1|=3，且a2+2a﹣3=5，解得a=2，故答案为2．【点评】本题考查交集、补集、并集的定义和运算，一元二次方程的解法．16．函数f（x）=的定义域为[﹣2，1]，则a的值为2．【考点】函数的定义域及其求法．【专题】转化思想；函数的性质及应用．【分析】根据二次根式的定义知（1﹣a2）x2+3（1﹣a）x+6≥0的解集是[﹣2，1]，结合一元二次方程根与系数的关系，求出a的值．【解答】解：由二次根式的定义，得（1﹣a2）x2+3（1﹣a）x+6≥0的解集是[﹣2，1]，∴（1﹣a2）＜0，且﹣2和1是方程（1﹣a2）x2+3（1﹣a）x+6=0 的2个根；∴﹣2+1=①，﹣2×1=②；解得a=2．故答案为：2．【点评】本题考查了求函数的定义域的问题，解题时应注意转化思想，把求函数的定义域转化为一元二次不等式的解集问题，是基础题．三．解答题（本大题共5小题，共48分.解答应写出必要的文字说明）17．已知函数f（x）的图象如图所示．（1）求函数f（x）的解析式；（2）求函数f（x）的定义域和值域．【考点】函数的图象．【专题】计算题；函数思想；数形结合法；函数的性质及应用．【分析】（1）使用待定系数法解出；（2）根据图象最左边到最右边的横坐标范围及定义域，最下边到最上边的纵坐标即为值域，去除取不到的点即可．【解答】解：（1）当﹣1≤x＜0时，设f（x）=ax+b，则，解得a=1，b=1，∴f（x）=x+1；当0≤x≤1时，设f（x）=kx，则k=﹣1，∴f（x）=﹣x，∴f（x）的解析式为f（x）=（2）定义域为[﹣1，1]，值域为[﹣1，1）【点评】本题考查了分段函数的解析式与图象，确定x在各段上的取值范围是关键，属于基础题．18．解下列不等式：（1）（2）|x﹣1|+|2x﹣1|＜3．【考点】其他不等式的解法．【专题】计算题；方程思想；综合法；不等式的解法及应用．【分析】分别分类讨论，即可求出不等式的解集．【解答】解：（1），∴或，∴x≥2，或﹣2≤x＜2，∴原不等式的解集为{x|﹣2≤x＜0或x≥2}；（2）当x≥1时，x﹣1+2x﹣1＜3，解得x＜，即1≤x＜，当≤x＜1时，1﹣x+2x﹣1＜3，解得x＜3，即≤x＜1，当x＜时，1﹣x+1﹣2x＜3，解得x＞﹣，即﹣＜x，综上所述，不等式的解集为．【点评】本题考查了不等式的解法，关键是分类讨论，属于基础题．19．已知集合A={x||x﹣1|＜2}，，U=R，求A∩B，A∪B，A∩（C U B）．【考点】其他不等式的解法；交、并、补集的混合运算．【专题】综合题；集合思想；定义法；不等式的解法及应用；集合．【分析】找出两集合中解集的公共部分，求出两集合的交集；找出既属于A又属于B的部分，求出两集合的并集；找出全集中不属于B的部分，求出B的补集，找出A与B补集的公共部分，即可确定出所求的集合．【解答】解：∵|x﹣1|＜2，∴﹣2＜x﹣1＜2，∴﹣1＜x＜3，∴A=（﹣1，3），∵≤0，∴x（x﹣1）（x﹣2）（x﹣4）≤0，且x=1，x=2，利用穿根法，如图所示，∴0≤x＜1，2＜x≤4，∴B=[0，1）∪（2，4]，∴C U B=（﹣∞，0）∪[1，2]∪（4，+∞），∴A∩B=[0，1）∪（2，3），A∪B=（﹣1，4]，A∩（C U B）=（﹣1，0）∪[1，2]．【点评】此题考查了交、并、补集的混合运算，熟练掌握交、并、补集的定义是解本题的关键．20．已知函数f（x）=的定义域为集合A，函数g（x）=x2﹣2x+a，x∈[0，4]的值域为集合B，若A∪B=R，求实数a的取值范围．【考点】函数的值域．【专题】函数的性质及应用．【分析】求解一元二次不等式得到A，利用配方法求函数的值域得到B，然后根据A∪B=R得到关于a的不等式组，求解不等式组得答案．【解答】解：由x2﹣2x﹣8≥0，得x≤﹣2或x≥4，∴A=（﹣∞，﹣2]∪[4，+∞），∵x∈[0，4]，∴g（x）=x2﹣2x+a=（x﹣1）2+a﹣1的最小值为a﹣1，最大值为a+8．∴B=[a﹣1，a+8]，由A∪B=R，∴，解得﹣4≤a≤﹣1．∴实数a的取值范围是[﹣4，﹣1]．【点评】本题考查了函数的定义域及值域的求法，考查了并集及其运算，是基础题．21．已知集合A={x|x2﹣3x+2=0}，B={x|x2+2（a+1）x+（a2﹣5）=0}，（Ⅰ）若B={2}，求实数a的值；（Ⅱ）若A∪B=A，求实数a的取值范围．【考点】函数的零点；并集及其运算．【专题】函数的性质及应用．【分析】由x2﹣3x+2=0解得x=1，2．可得 A={1，2}．（Ⅰ）由B={2}，可得，解得即可．（Ⅱ）由A∪B=A，可得B⊆A．分类讨论：B=∅，△＜0，解得即可．若B={1}或{2}，则△=0，解得即可．若B={1，2}，可得，此方程组无解．【解答】解：由x2﹣3x+2=0解得x=1，2．∴A={1，2}．（Ⅰ）∵B={2}，∴解得a=﹣3．（Ⅱ）∵A∪B=A，∴B⊆A．1°B=∅，△=8a+24＜0，解得a＜﹣3．2°若B={1}或{2}，则△=0，解得a=﹣3，此时B={2}，符合题意．3°若B={1，2}，∴，此方程组无解．综上：a≤﹣3．∴实数a的取值范围是（﹣∞，﹣3]．【点评】本题考查了集合之间的关系、一元二次方程的解与判别式△的关系，属于中档题．。

山西大学附中2014~2015学年高一第一学期期中考试（总第二次）数学试题考试时间：90分钟 满分：100分一、选择题（本大题共10小题，每小题4分，共40分）1．设全集{}*|6U x N x =∈<，集合{}{}1,3,3,5A B ==，则()U C A B =( )A ．{}2,4B ．{}1,5C ．{}1,4D ．{}2,52． 函数()lg(2)f x x =+的定义域为( ) A ．(2,1)-B ．[2,1)-C ．(2,1]-D ．[]1,2-3．已知0a >且1a ≠，下列四组函数中表示相等函数的是( )A ．log a y x = 与1(log )x y a -=B ．2y x =与2log x a y a =C ．log a xy a=与y x = D ．2log a y x =与2log a y x =4．已知函数21()21x x f x -=+,若()f a b =， 则()f a -=( )A ．bB ．b -C ．1bD ．1b-5．下列函数中值域为()0,+∞的是( )A ．xy -=215 B ．()10y x x x =+> C ．xy -⎪⎭⎫⎝⎛=131D ．()11y x x x=-≥6．已知幂函数()y f x =的图像过点(,则4log (2)f 的值为( )A ．14 B ．14- C ．2 D ．2- 7．在下列区间中，函数()43xf x e x =+-的零点所在的区间为( )A ．1,04⎛⎫- ⎪⎝⎭B ．10,4⎛⎫ ⎪⎝⎭C ．11,42⎛⎫ ⎪⎝⎭D ．13,24⎛⎫ ⎪⎝⎭8．三个数 3.3320.99,log ,log 0.8π的大小关系为( )A ． 3.332log 0.99log 0.8π<<B ． 3.323log 0.8log 0.99π<<C ． 3.3230.99log 0.8l og π<<D ． 3.323log 0.80.99log π<< 9．当(1,2)x ∈，不等式2(1)log a x x -<恒成立，则实数a 的取值范围是（ ）A ．(1,2)B ．(1,2]C ．[)2,+∞ D ．(2,)+∞10．若函数()f x 为定义在R 上的奇函数，且在()0,+∞为增函数，又(2)f 0=，则不等式[]1ln ()0x f x e ⎛⎫⋅⋅< ⎪⎝⎭的解集为( ) A ．()()2,02,-+∞ B ．()(),20,2-∞-C ．()()2,00,2-D ．()(),22,-∞-+∞二、填空题：（本大题共5小题，每小题4分，共20分）11．函数()log 12a y x =++(01)a a >≠且恒过定点，其坐标为 ．12．设1232,2()log (1),2x e x f x x x -⎧<⎪=⎨-≥⎪⎩，则((2))f f 的值为 ．13．已知函数()xf x e x =+，若关于x 的方程()f x k =有两个不同的实根，则实数k 的取值范围是 ．14．已知函数)(x f 满足：)()()(q f p f q p f ⋅=+，2)1(=f ，则：)2013()2014()7()8()5()6()3()4()1()2(f f f f f f f f f f +++++ = ． 15． 给出下列四个命题：①函数2212-+-=x x y 为奇函数；②奇函数的图像一定通过直角坐标系的原点； ③函数xy 12=的值域是()0,+∞；④若函数)2(x f 的定义域为[1,2]，则函数)2(xf 的定义域为[1,2]； ⑤函数()x x y 2lg 2+-=的单调递增区间是(]0,1．其中正确命题的序号是 ．（填上所有正确命题的序号）三、解答题（本大题共5小题，共40分．解答应写出必要的文字说明，证明过程或演算步骤）16．（本小题满分8分）计算：（Ⅰ）()20.532025270.1100964π--⎛⎫⎛⎫++-⋅⎪ ⎪⎝⎭⎝⎭；（Ⅱ）82715lg lg lg12.5log 9log 828-+-⋅+2ln 2e ．17．（本小题满分8分）已知集合{}22|280A x x ax a =--≤． （Ⅰ）当1a =时，求集合R C A ；（Ⅱ）若0a >，且(1,1)A -⊆，求实数a 的取值范围．18．（本小题满分8分）已知二次函数a ax x x f -+-=2)(2在区间[]0,1上有最大值2，求实数a 的值．19．()1,1-上的函数． （Ⅰ）用定义法证明函数()x f 在()1,1-上是增函数； （Ⅱ）解不等式()()01<+-x f x f ．20．（本小题满分8分）已知函数4()log (41)()x f x kx k R =++∈是偶函数． （Ⅰ）求k 的值；（Ⅱ）设44()log (2)3x g x a a =⋅-,若函数()f x 与()g x 的图象有且只有一个公共点，求实数a 的取值范围．山西大学附中2014~2015学年高一第一学期期中考试（总第二次）数学答案二、填空题：（本大题共5小题，每小题4分，共20分）11． ()0,2 12． 2． 13．()1,+∞ 14．2014 15．①④⑤三、解答题（本大题共5小题，共40分．解答应写出必要的文字说明，证明过程或演算步骤）16．（本小题满分8分）计算：（Ⅰ）()20.532025270.1100964π--⎛⎫⎛⎫++-⋅⎪ ⎪⎝⎭⎝⎭； （Ⅱ）82715lg lg lg12.5log 9log 828-+-⋅+2ln 2e ．解：（Ⅰ）319；……………………4分 （Ⅱ）133……………………8分17．（本小题满分8分）已知集合{}22|280A x x ax a =--≤． （Ⅰ）当1a =时，求集合R C A ；（Ⅱ）若0a >，且(1,1)A -⊆，求实数a 的取值范围．解：（Ⅰ）当1=a 时，解不等式0822≤--x x ，得42≤≤-x …………………2分 ∴{}|42R C A x x x =><-或 ………………………………………3分 （Ⅱ）∵22280x ax a --≤，∴0)2)(4(≤+-a x a x又∵0a > ∴24a x a -≤≤ ∴[]2,4A a a =- ……………………5分 又∵()1,1A -⊆ ∴1214aa-≥-⎧⎨≤⎩ …………………………………………7分解得21≥a ，故实数a 的取值范围是1[,)2+∞ …………………………………8分 18．（本小题满分8分）已知二次函数a ax x x f -+-=2)(2在区间[]0,1上有最大值2，求实数a 的值解析：由a a a x x f -+--=22)()(，得函数)(x f 的对称轴为：x a =，……1分 ①当0<a 时，()f x 在]1,0[上递减， 2)0(=∴f ，即2,2-=∴=-a a ； ……………………3分 ②当1>a 时，()f x 在]1,0[上递增， 2)1(=∴f ，即3=a ； ……………………5分③当01a ≤≤时，()f x 在],0[a 递增，在[,1]a 上递减，2)(=∴a f ，即22=-a a ，解得：12-=或a 与01a ≤≤矛盾；……………7分 综上：2a =-或3a = ……………………8分19．（本小题满分8()1,1-上的函数． （Ⅰ）用定义法证明函数()x f 在上是增函数；（Ⅱ）解不等式()()01<+-x f x f ．解：（Ⅰ）证明：对于任意的()1,1,21-∈x x ，且21x x <，则()()()()()()()()()()()()()()22212121222112212122212122212222112111111111111x x x x x x x x x x x x x x x x x x x x x x x x x f x f ++--=++-+-=+++-+=+-+=- 1121<<<-x x ， ()()011,0222121>++<-∴x x x x ，01,12121>-∴<∴x x x x ． ()()021<-∴x f x f ，即()()21x f x f <．∴函数()21xf x x =+在()1,1-上是增函数．…………………… 4分 （Ⅱ）由已知及（Ⅰ）知，()f x 是奇函数且在()1,1-上递增，()()()()()()2102111201111111101<<⇔⎪⎪⎩⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧<<<-<<⇔-<-<<-<-<-⇔-<-⇔-<-⇔<+-x x x x x x x x x f x f x f x f x f x f ∴不等式的解集为10,2⎛⎫⎪⎝⎭．…… 8分．20．（本小题满分8分）已知函数4()log (41)()x f x kx k R =++∈是偶函数． （Ⅰ）求k 的值；（Ⅱ）设44()log (2)3x g x a a =⋅-,若函数()f x 与()g x 的图象有且只有一个公共点，求实数a 的取值范围． 解：（Ⅰ）由函数()f x 是偶函数，可知()().f x f x =-kx kx x x -+=++∴-)14(log )14(log 44,kx x x 21414log 4-=++-即, ,24log 4kx x -= 2x kx ∴=-对一切 x R ∈恒成立21-=∴k ……………3分（Ⅱ）函数()f x 与()g x 的图象有且只有一个公共点,即方程4414log (41)log (2)23x x x a a +-=⋅-有且只有一个实根,化简得: 方程142223x x x a a +=⋅-有且只有一个实根 ……………………4分令20x t =>,则方程24(1)103a t at ---=有且只有一个正根,①314a t =⇒=-,不合题意; ……………………5分②若304a ∆=⇒=或3-；若3,24a t ==-则,不合题意；若132a t =-⇒= ,符合题意③若方程一个正根与一个负根,即1011a a -<⇒>- ……………………7分综上:实数a 的取值范围是{}3(1,)-⋃+∞ ……………………8分。

山西大学附中2014—2015学年第一学期高二（10月）月考数学试题考试时间：90分钟一.选择题（每小题3分,满分30分,在每小题给出的四个选项中,只有一项是符合题目要求的） 1．圆心在)1,2(-上，半径为3的圆的标准方程为（ ） A. 3)1()2(22=++-y xB. 9)1()2(22=++-y xC. 3)1()2(22=-++y xD. 9)1()2(22=-++y x 2．经过两点(4,21)A y +，(2,3)B -的直线的倾斜角为34π，则y = ( ) A.－1 B.－3 C.0 D.23．已知倾斜角为α的直线l 与直线220x y -+=平行，则tan 2α的值( ) A ．45B ．43C ．34D ．234．若直线04)2()52(=+-++y a x a 与直线01)3()2(=-++-y a x a 互相垂直，则a 的值等于（ ）A ． 2B ．－2C ．2,－2D ．2,0,－25.已知三点()3,1A 、()2,B k -、()8,11C 共线，则k 的取值是（ ） A.6- B.7- C.8- D ．9-6.如右图，直线123,,l l l 的斜率分别为123,,k k k ，则A.123k k k <<B.312k k k <<C.321k k k <<D.132k k k <<7、经过点(1,1)M 的直线与坐标轴所围成的三角形面积为3A ．4条B ．3条C ．2条D ．1条8．点(,)M x y 在函数28y x =-+的图象上，当[2,5]x ∈时，11y x ++的取值范围是( ) A ．1[,2]6- B ．5[0,]3C ．15[,]63- D ．[2,4]9．设点(2,3),(3,2)A B -，若直线20ax y ++=与线段AB 没有交点，则a 的取值范围是( )A. 54(,)(,)23-∞-⋃+∞ B. 45(,)32-C. 54(,)23-D. 45(,)(,)32-∞-⋃+∞10．从点(,3)P m 向圆22(2)(2)1x y +++=作切线，切线长最小值等于（ ）A. 2B. 4C. 5D.二.填空题（每题4分,满分16分,把答案填在题中横线上）11．设y kx z +=，其中实数y x ,满足⎪⎩⎪⎨⎧≤--≥+-≥-+04204202y x y x y x ，若z 的最大值为12，则实数=k ________。

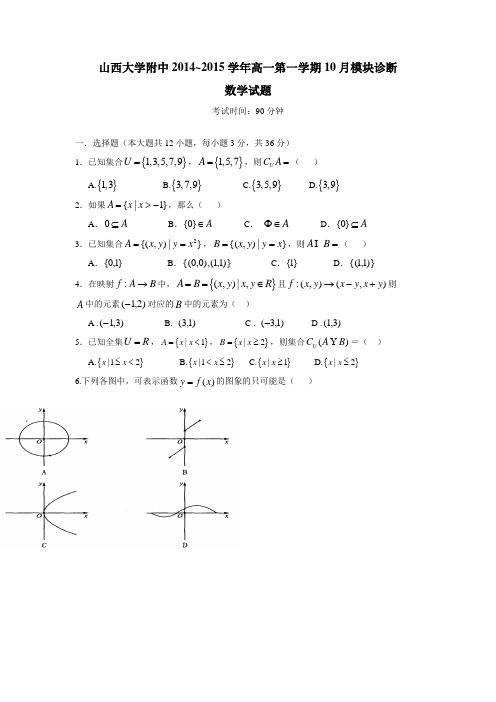
山西大学附中2014~2015学年高一第一学期10月模块诊断数学试题考试时间：90分钟一．选择题（本大题共12小题，每小题3分，共36分） 1．已知集合{}1,3,5,7,9U =，{}1,5,7A =，则U C A =（ ） A.{}1,3B.{}3,7,9C.{}3,5,9D.{}3,92．如果}1|{->=x x A ，那么（ ）A ．A ⊆0B ．A ∈}0{C ． A ∈ΦD ．A ⊆}0{ 3．已知集合}|),{(2x y y x A ==，}|),{(x y y x B ==，则=B A （ ） A ．}1,0{ B ．)}1,1(),0,0{( C ．}1{ D ．)}1,1{( 4．在映射:f A B →中，{}(,)|,A B x y x y R ==∈且:(,)(,)f x y x y x y →-+则A 中的元素)2,1(-对应的B 中的元素为（ ）A .)3,1(- B. )1,3( C . )1,3(- D .)3,1(5．已知全集R U =，{}|1A x x =<，{}|2B x x =≥，则集合)(B A C U ＝（ ） A.{}|12x x ≤< B.{}|12x x <≤ C.{}|1x x ≥ D.{}|2x x ≤ 6.下列各图中，可表示函数)(x f y =的图象的只可能是（ ）7．若全集R U =， 集合=A {}1|0,|1x x B x x x -⎧⎫<=≥⎨⎬⎩⎭， 则}0|{≤x x 等于( ) A. B A B. B A C. )(B A C U D. )(B A C U8．已知⎩⎨⎧<+≥-=6)2(65)(x x f x x x f ，则)3(f 为（ ）A ． 2B ． 3C ． 4D ． 5 9．已知集合{32,},{6,8,10,12,14}A x x n n N B ==+∈=，则集合A B 的子集个数为( )A. 2B.4C.6D.8 10.函数()x f y =的定义域是[]2,0 ，则函数1)2(-=x x f y 的定义域是（ ） A. []1,0 B. )1,0[ C.]4,1()1,0[ D. )1,0(11．有下列四个命题：①{}0是空集；②若N a ∈，则a N -∉；③集合{}2210A x R x x =∈-+=有两个元素；④集合6B x Q N x ⎧⎫=∈∈⎨⎬⎩⎭是有限集，其中正确命题的个数是（ ）A ．0B ．1C ．2D ．3 12．已知1(0)()0(0)x f x x ≥⎧=⎨<⎩ ，则不等式()2xf x x +≤的解集为（ ）A ．[]0,1B ．[]0,2C ．](,1-∞D ． ](,2-∞二．填空题（本大题共4小题，每小题4分,共16分.）13．已知函数02)(x x x f ++=的定义域为14．已知全集}8,7,6,5,4,3,2,1{=U ，}4,3,1{)(=B A C U ,}7,5{)()(=B C A C U U},2{=B A 则集合=A15．已知全集}5{},2|,12{|},32,3,2{2=-=-+=A C a A a a U u ，则实数a ＝ .16．函数6)1(3)1()(22+-+-=x a x a x f ，若)(x f 的定义域为]1,2[-，则实数a的值为 .三．解答题（本大题共5小题，共48分.解答应写出必要的文字说明） 17.(本题满分8分)已知函数)(x f 的图象如图所示。

山西大学附中2014~2015学年高一第一学期10月（总第一次）月考数学试题考试时间：100分钟 满分：100分 一、选择题（本大题共10小题，每小题4分，共40分．） 1．已知集合{}1,3,5,7,9U =，{}1,5,7A =，则U C A =（ ） A.{}1,3B.{}3,7,9C.{}3,5,9D.{}3,92．图中阴影部分所表示的集合是（ ）A. )(C A C B U ⋃⋂B. ()()C B B A ⋃⋃⋃C. ()()B C C A U ⋂⋃D. ()C A C B U ⋂⋃3．若},4,2,0{},2,1,0{,,==⊆⊆Q P Q M P M 则满足上述条件的集合M 的个数是（ ） A ．4 B ．3 C ．2 D ．14.已知集合{}{}20,40≤≤=≤≤=y x Q x x P ，下列不能表示从P 到Q 的映射的是（ ） A ．x y x f 21:=→ B ．x y x f 32:=→ C ．281:x y x f =→ D ．x y x f =→: 5．已知集合2{0,},{|250,}P m Q x x x x Z ==-<∈，若P Q ≠∅，则m 等于（ ）A ．1B ．2C ．1或25D ．1或2 6．若函数)(x f 对任意0>a 且1≠a ，都有)()(x af ax f =，则称函数为“穿透”函数，则下列函数中，不是“穿透”函数的是( )A. x x f -=)(B. 1)(+=x x fC. x x f =)(D. x x x f -=)(7．已知x x g 21)(-=，[])0(1)(22≠-=x x x x g f ,则)21(f 等于（ ） A.1 B.3 C.15 D.308.已知集合},54|{},,1|{22**∈+-==∈+==N n n n x x Q N m m x x P ，则（ ）A ．Q P =B ．P Q ⊂≠C ．Q P ⊂≠D ．以上皆错9．设函数⎩⎨⎧<+≥+-=0,60,64)(2x x x x x x f ，则不等式)1()(f x f >的解集是（ ）A ．),3()1,3(+∞-B ．),2()1,3(+∞-C ．),3()1,1(+∞-D ．)3,1()3,( --∞二、填空题：（本大题共5小题，每小题4分,共20分.） 11．不等式211>x 的解集是 ． 12．定义},,,|{B y A x yxxy z z B A ∈∈+==⊗设集合}2,0{=A ，}1{},2,1{==C B ，则集合C B A ⊗⊗)(的所有元素之和为 ．13．若不等式20ax bx c ++>的解集为⎭⎬⎫⎩⎨⎧<<4151x x ，则不等式0222<--a bx cx 的解集为 ．14．已知函数1)(+=ax x f 在(]1,∞-上有意义，则实数a 的取值范围为 ． 15．有下列五个命题：①若B A =Φ，则B A ,之中至少有一个为空集；②函数y {}1≥x x ；③集合{}2210A x R x x =∈-+=有两个元素； ④函数)(2Z x x y ∈=的图象是一直线；⑤不等式()()06422≤--x x 的解集是{}622=≤≤-x x x 或.其中错误命题的序号是 ． 三、解答题（本大题共5小题，共40分.解答应写出必要的文字说明，证明过程或演算步骤.） 16．（本小题满分8分）已知全集为R ,集合{}0652≥+-=x x x A ，集合}31|{<+=x x B .求:（Ⅰ）B A ⋃； （Ⅱ）B A C R ⋂)(．17．（本小题满分8分）求下列函数的定义域：（Ⅰ）14)(2+-=x x x f ； （Ⅱ）132)(++-=x x x f ．18．（本小题满分8分）如图，用长为12米的铁丝弯成下部为矩形，上部为半圆形的框架窗户，若半圆半径为x 米．（Ⅰ）求此框架围成的面积y 与x 的函数式)(x f y =，并写出它的定义域； （Ⅱ）求半圆的半径是多长时，窗户透光的面积最大？19．（本小题满分8分）已知二次函数x ax x f +=2)(有最小值，不等式0)(<x f 的解集为A ．（Ⅰ）求集合A ；（Ⅱ）设集合{}a x x B <+=4，且B B A =⋂,求实数a 的取值范围.20．(本小题满分8分)已知集合{}022≤--=x x x A ，不等式022≤---a ax x 在集合A 上恒成立，求实数a 的取值范围.山西大学附中2014~2015学年高一第一学期10月（总第一次）月考数学答案二．填空题：（本大题共5小题，每小题4分，共20分）11．(0,2) 12．18 13．{}110>-<x x x 或 14. []0,1- 15. ①②③④三．解答题：（本题共5大题，共40分） 16．（本小题满分8分）解： {}{}320652≥≤=≥+-=x x x x x x A 或……………2分()2,4}31|{-=<+=x x B ……………4分∴()3,2)(=A C R∴（Ⅰ）{}32|≥≤=x x x B A 或 ……………6分 （Ⅱ）B A C R ⋂)(=Φ ……………8分17．（本小题满分8分）答案：（Ⅰ）{}122-≠≤≤-x x x 且 ………4分 （Ⅱ）{}11≥-<x x x 或……8分 18．（本小题满分8分）解：（Ⅰ）由题意可知：下部为矩形且一边长x AB 2=米，另一边长2212xx AD --=π米…………2分∴x x x x x x x f 1222221222)(22+⎪⎭⎫ ⎝⎛+-=--⋅+=πππ …………4分由⎪⎩⎪⎨⎧>-->022120x x x π得2120+<<πx∴函数的定义域为⎪⎭⎫⎝⎛+212,0π …………6分（Ⅱ）⎪⎭⎫ ⎝⎛+∈212,0πx 且函数)(x f y =图像开口向下∴当412+=πx 时，函数取得最大值. ∴当半圆的半径412+=πx 时，窗户透光的面积最大. …………8分 19．（本小题满分8分）解：（Ⅰ） 二次函数x ax x f +=2)(有最小值 0>∴a …………1分∴0100)(2<<-⇔<+⇔<x ax ax x f ∴集合⎪⎭⎫⎝⎛-=0,1a A ． …………3分（Ⅱ）集合{}()4,44---=<+=a a a x x B …………5分B B A =⋂ ∴A B ⊆ ∴25004140-≤<⇔⎪⎪⎩⎪⎪⎨⎧≤--≥-->a a a a a∴实数a 的取值范围为(]25,0-． …………8分20．(本小题满分8分)解：集合{}[]2,1022-=≤--=x x x A ………2分设2)(2---=a ax x x f ，由)(x f 的图象可知：当方程022=---a ax x 的小根11-≤x ，大根22≥x 时，即可满足题意 …………5分∴⎩⎨⎧≤≤-0)2(0)1(f f 323201≥⇔⎩⎨⎧≤-≤-⇔a a ∴实数a 的取值范围为⎪⎭⎫⎢⎣⎡+∞,32. …………8分另解：。

山西省山大附中高一10月月考（数学）考试时间：80分钟一、选择题：（每小题4分，共40分）1．已知集合{}1,3,5,7,9U =，{}1,5,7A =，则U C A =（ ） A.{}1,3 B.{}3,7,9 C.{}3,5,9 D.{}3,9 2．已知集合2{0,},{|250,}P m Q x x x x Z ==-<∈，若P Q ≠∅，则m 等于（ ）A ．1B ．2C ．1或25D ．1或23．已知集合{}{}21,3,,,1A x B x ==，由集合A B 与的所有元素组成集合{}1,3,x 这样的实数x 共有（ ）A ．1个B ．2个C ．3个D ．4个4．设3x y ==+，集合{},M m m a a Q b Q ==+∈∈，那么,x y 与集合M 的关系是（ ）A ．,x M y M ∈∈B ．,x M y M ∈∉C ．,x M y M ∉∈D ．,x M y M ∉∉5．有下列四个命题：①{}0是空集；②若N a ∈，则a N -∉；③集合{}2210A x R x x =∈-+=有两个元素；④集合6B x Q N x⎧⎫=∈∈⎨⎬⎩⎭是有限集，其中正 确命题的个数是 （ ）A ．0B ．1C ．2D ．36.函数()x f y =的定义域是[]20、，则函数()1+=x f y 的定义域是（ ） A []20、B []11、-C []02、-D []31、 7.函数()()()⎩⎨⎧≥<<=2..........321....2x x x x f ，则⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛23f f 等于（ ） A 2 B 3 C 4 D 6 8.函数 f(x)=2x11+ 的值域是（ ） A.(0,1) B.[0,1) C.(0，1] D. (]1,∞-9. 设集合{}1,2,3A =，{}4,5,6B =，定义映射f ：A B →，使对任意x A ∈，都有22()()x f x x f x ++是奇数，则这样的映射f 的个数为 （ ）.A 7 .B 9 .C 10 .D 1810. 已知函数⎪⎩⎪⎨⎧<-≥+=0,40,4)(22x x x x x x x f ，若2(2)(),f a f a ->则实数a 的取值范围是A.(,1)(2,)-∞-⋃+∞B. (1,2)-C. (2,1)-D. (,2)(1,)-∞-⋃+∞ 二．填空题：（每空4分，共16分）11．已知全集}5{},2|,12{|},32,3,2{2=-=-+=A C a A a a U u ，则实数a ＝ .12．函数3232-+-=x x y 的单调增区间是 ；13．满足条件{1,2,3}⊂≠M ⊂≠{1,2,3,4,5,6}的集合M 的个数是14. 已知x x x f 2)1(+=+，则=)(x f 。

山西大学附中2014~2015学年高一第一学期10月（总第一次）模块诊断数学试题考试时间：90分钟一．选择题（本大题共12小题，每小题3分，共36分） 1．已知集合{}1,3,5,7,9U =，{}1,5,7A =，则U C A =（ ） A.{}1,3B.{}3,7,9C.{}3,5,9D.{}3,92．如果}1|{->=x x A ，那么（ ）A ．A ⊆0B ．A ∈}0{C ．A ∈ΦD ．A ⊆}0{3．已知集合}|),{(2x y y x A ==，}|),{(x y y x B ==，则=B A （ ） A ．}1,0{ B ．)}1,1(),0,0{( C ．}1{ D ．)}1,1{( 4．在映射:f A B →中，{}(,)|,A B x y x y R ==∈且:(,)(,)f x y x y x y →-+则A 中的元素)2,1(-对应的B 中的元素为（ ）A .)3,1(- B. )1,3( C . )1,3(- D .)3,1(5．已知全集R U =，{}|1A x x =<，{}|2B x x =≥，则集合)(B A C U ＝（ ）A.{}|12x x ≤<B.{}|12x x <≤C.{}|1x x ≥D.{}|2x x ≤ 6.下列各图中，可表示函数)(x f y =的图象的只可能是（ ）7．若全集R U =， 集合=A {}1|0,|1x x B x x x -⎧⎫<=≥⎨⎬⎩⎭， 则}0|{≤x x 等于( ) A. B A B. B A C. )(B A C U D. )(B A C U8．已知⎩⎨⎧<+≥-=6)2(65)(x x f x x x f ，则)3(f 为（ ）A ． 2B ． 3C ． 4D ． 5 9．已知集合{32,},{6,8,10,12,14}A x x n n N B ==+∈=，则集合A B 的子集个数为( )A. 2B.4C.6D.810.函数()x f y =的定义域是[]2,0 ，则函数1)2(-=x x f y 的定义域是（ ） A. []1,0 B. )1,0[ C.]4,1()1,0[ D. )1,0(11．有下列四个命题：①{}0是空集；②若N a ∈，则a N -∉；③集合{}2210A x R x x =∈-+=有两个元素；④集合6B x Q N x ⎧⎫=∈∈⎨⎬⎩⎭是有限集，其中正确命题的个数是（ ）A ．0B ．1C ．2D ．3 12．已知1(0)()0(0)x f x x ≥⎧=⎨<⎩，则不等式()2xf x x +≤的解集为（ ）A ．[]0,1B ．[]0,2C ．](,1-∞ D ． ](,2-∞二．填空题（本大题共4小题，每小题4分,共16分.）13．已知函数02)(x x x f ++=的定义域为14．已知全集}8,7,6,5,4,3,2,1{=U ，}4,3,1{)(=B A C U ,}7,5{)()(=B C A C U U},2{=B A 则集合=A15．已知全集}5{},2|,12{|},32,3,2{2=-=-+=A C a A a a U u ，则实数a ＝ .16．函数6)1(3)1()(22+-+-=x a x a x f ，若)(x f 的定义域为]1,2[-，则实数a的值为 .三．解答题（本大题共5小题，共48分.解答应写出必要的文字说明） 17.(本题满分8分)已知函数)(x f 的图象如图所示。

1．已知集合{}1,3,5,7,9U =，{}1,5,7A =，则U C A =（ ） A.{}1,3B.{}3,7,9C.{}3,5,9D.{}3,9 2．图中阴影部分所表示的集合是（ ）A. )(C A C B U ⋃⋂B. ()()C B B A ⋃⋃⋃C. ()()B C C A U ⋂⋃D. ()C A C B U ⋂⋃3．若},4,2,0{},2,1,0{,,==⊆⊆Q P Q M P M 则满足上述条件的集合M 的个数是（ ） A ．4 B ．3 C ．2 D ．14.已知集合{}{}20,40≤≤=≤≤=y x Q x x P ，下列不能表示从P 到Q 的映射的是（ ） A ．x y x f 21:=→ B ．x y x f 32:=→ C ．281:x y x f =→ D ．x y x f =→: 5．已知集合2{0,},{|250,}P m Q x x x x Z ==-<∈，若P Q ≠∅，则m 等于（ ）A ．1B ．2C ．1或25D ．1或2 6．若函数)(x f 对任意0>a 且1≠a ，都有)()(x af ax f =，则称函数为“穿透”函数，则下列函数中，不是“穿透”函数的是( )A. x x f -=)(B. 1)(+=x x fC. x x f =)(D. x x x f -=)(7．已知x x g 21)(-=，[])0(1)(22≠-=x x x x g f ,则)21(f 等于（ ）A.1B.3C.15D.308.已知集合},54|{},,1|{22**∈+-==∈+==N n n n x x Q N m m x x P ，则（ ）A ．Q P =B ．P Q ⊂≠C ．Q P ⊂≠D ．以上皆错9．设函数⎩⎨⎧<+≥+-=0,60,64)(2x x x x x x f ，则不等式)1()(f x f >的解集是（ ）A ．),3()1,3(+∞-B ．),2()1,3(+∞-C ．),3()1,1(+∞-D ．)3,1()3,( --∞ 10．已知)(x f 满足)()(x f x f -=-，且当0>x 时，2)(-=x x x f ，则当0<x 时，)(x f 的表达式为（ ）A ．2)(+=x x x fB ．2)(-=x x x fC ．2)(+-=x x x fD ．2)(--=x x x f 二、填空题：（本大题共5小题，每小题4分,共20分.） 11．不等式211>x 的解集是 ． 12．定义},,,|{B y A x yxxy z z B A ∈∈+==⊗设集合}2,0{=A ，}1{},2,1{==C B ，则集合C B A ⊗⊗)(的所有元素之和为 ． 13．若不等式20ax bx c ++>的解集为⎭⎬⎫⎩⎨⎧<<4151x x ，则不等式0222<--a bx cx 的 解集为 ． 14．已知函数1)(+=ax x f 在(]1,∞-上有意义，则实数a 的取值范围为 ．15．有下列五个命题：①若B A =Φ，则B A ,之中至少有一个为空集；②函数y =的定义域为{}1≥x x ；③集合{}2210A x R x x =∈-+=有两个元素； ④函数)(2Z x x y ∈=的图象是一直线； ⑤不等式()()06422≤--x x的解集是{}622=≤≤-x x x 或.其中错误命题的序号是 ． 三、解答题（本大题共5小题，共40分.解答应写出必要的文字说明，证明过程或演算步骤.） 16．（本小题满分8分）已知全集为R ,集合{}0652≥+-=x xx A ，集合}31|{<+=x x B .求:（Ⅰ）B A ⋃； （Ⅱ）B A C R ⋂)(．17．（本小题满分8分）求下列函数的定义域：（Ⅰ）14)(2+-=x x x f ； （Ⅱ）132)(++-=x x x f ．已知二次函数x ax x f +=2)(有最小值，不等式0)(<x f 的解集为A ． （Ⅰ）求集合A ；（Ⅱ）设集合{}a x x B <+=4，且B B A =⋂,求实数a 的取值范围.20．(本小题满分8分)已知集合{}022≤--=x x x A ，不等式022≤---a ax x 在集合A 上恒成立，求实数a 的取值范围.山西大学附中2014~2015学年高一第一学期10月（总第一次）月考数学答案二．填空题：（本大题共5小题，每小题4分，共20分）11．(0,2) 12．18 13．{}110>-<x x x 或 14. []0,1- 15. ①②③④三．解答题：（本题共5大题，共40分）16．（本小题满分8分）解： {}{}320652≥≤=≥+-=x x x x x x A 或……………2分()2,4}31|{-=<+=x x B ……………4分∴()3,2)(=A C R∴（Ⅰ）{}32|≥≤=x x x B A 或 ……………6分 （Ⅱ）B A C R ⋂)(=Φ ……………8分17．（本小题满分8分）答案：（Ⅰ）{}122-≠≤≤-x x x 且 ………4分 （Ⅱ）{}11≥-<x x x 或……8分 18．（本小题满分8分）解：（Ⅰ）由题意可知：下部为矩形且一边长x AB 2=米，另一边长2212xx AD --=π米…………2分∴x x x x x x x f 1222221222)(22+⎪⎭⎫ ⎝⎛+-=--⋅+=πππ …………4分由⎪⎩⎪⎨⎧>-->022120x x x π得2120+<<πx∴函数的定义域为⎪⎭⎫ ⎝⎛+212,0π …………6分（Ⅱ）⎪⎭⎫ ⎝⎛+∈212,0πx 且函数)(x f y =图像开口向下∴当412+=πx 时，函数取得最大值. ∴当半圆的半径412+=πx 时，窗户透光的面积最大. …………8分 19．（本小题满分8分）解：（Ⅰ） 二次函数x ax x f +=2)(有最小值 0>∴a …………1分∴0100)(2<<-⇔<+⇔<x ax ax x f ∴集合⎪⎭⎫⎝⎛-=0,1a A ． …………3分（Ⅱ）集合{}()4,44---=<+=a a a x x B …………5分 B B A =⋂ ∴A B ⊆ ∴25004140-≤<⇔⎪⎪⎩⎪⎪⎨⎧≤--≥-->a a a a a∴实数a 的取值范围为(]25,0-． …………8分20．(本小题满分8分)解：集合{}[]2,1022-=≤--=x x x A ………2分设2)(2---=a ax x x f ，由)(x f 的图象可知：当方程022=---a ax x 的小根11-≤x ，大根22≥x 时，即可满足题意 …………5分∴⎩⎨⎧≤≤-0)2(0)1(f f 323201≥⇔⎩⎨⎧≤-≤-⇔a a ∴实数a 的取值范围为⎪⎭⎫⎢⎣⎡+∞,32. …………8分另解：。

山西大学附中2014年高三第一学期10月月考数学试题考试时间：120分钟 总分为：100分 考查内容：高中全部 一．选择题〔本大题共12题，每一小题3分，共36分.〕1．设集合}log ,3{2a P =，{}b a Q ,=，假设}0{=Q P ，如此=Q P A.{}0,3 B.{}2,0,3 C.{}1,0,3 D.{}2,1,0,3 2．命题:,sin 1,p x R x ∀∈≤如此p ⌝是A ．,sin 1x R x ∃∈≥B ．,sin 1x R x ∀∈≥C ．,sin 1x R x ∃∈>D ．,sin 1x R x ∀∈>3.实数y x ,满足(01)x y a a a <<<，如此如下关系式恒成立的是 A.33x y > B.sin sin x y > C.22ln(1)ln(1)x y +>+ D.221111x y >++ 4.曲线2-=x xy 在点)1,1(-处的切线方程为A. 32+-=x yB. 32--=x yC. 12+-=x yD.12+=x y5.假设31)6sin(=+απ，如此)3cos(απ-的值为A ．12-B ．12C ．13-D ．136．ABC ∆中，,,a b c 分别为,,A B C 的对边，cos cos a A b B =，如此ABC ∆为 A ．等腰三角形 B ．直角三角形 C ．等腰直角三角形 D ．等腰或直角三角形 7．偶函数)(x f 的定义域为R ，如此如下函数中为奇函数的是A.)](sin[x fB.)(sin x f x ⋅C.)(sin )(x f x f ⋅D.2)](sin [x f8.将函数)3cos(π-=x y 的图像上各点的横坐标伸长到原来的2倍〔纵坐标不变〕，再向左平移6π个单位，所得图像的一条对称轴方程为A.9π=x B.8π=x C.2π=x D.π=x9.函数|1|||ln --=x e y x 的图象大致是10．函数)42sin(log 21π+=x y 的单调减区间为A ．)(,4Z k k k ∈⎥⎦⎤ ⎝⎛-πππB ．)(8,8Z k k k ∈⎥⎦⎤ ⎝⎛+-ππππC ．)(8,83Z k k k ∈⎥⎦⎤ ⎝⎛+-ππππD ．)(83,8Z k k k ∈⎥⎦⎤ ⎝⎛++ππππ11．函数*()21,f x x x =+∈N .假设*0,x n ∃∈N ，使000()(1)()63f x f x f x n +++++=成立,如此称0(,)x n 为函数()f x 的一个“生成点〞.如此函数()f x 的“生成点〞共有__个A.1个 B .2个 C .3个 D .4个12．假设定义在R 上的函数)(x f 的导函数为()f x '，且满足()()f x f x '>，如此(2011)f 与2(2009)f e 的大小关系为A.2)2009()2011(e f f >B.2)2009()2011(e f f =C.2)2009()2011(e f f <D. 不能确定二．填空题〔本大题共4小题，每一小题3分，共12分.〕13．复数112z i=-，如此12111z z z +=-的虚部是.14. 方程33x x k -=有3个不等的实根, 如此常数k 的取值范围是 .15．定义在R 上的函数)(x f 满足⎩⎨⎧>---≤-=0),2()1(0),8(log )(2x x f x f x x x f ，如此=)2013(f .16．在锐角ABC ∆中，角,,A B C 的对边分别为,,a b c ，假设6cos b aCa b +=，如此 tan tan C A ＋tan tan CB 的值是________．三.解答题(本大题共6小题,共52分.)17.〔此题总分为8分〕函数221()sin ()cos ()42f x x x x R π=+++∈〔1〕求函数)(x f 的最值与最小正周期；〔2〕求使不等式],0[(23)(π∈≥x x f 〕成立的x 的取值范围．18.〔此题总分为8分〕数列{}n a 的前n 项和，122++=n n S n.〔1〕求数列{}n a 的通项公式n a ；〔2〕记132211...11++++=n n n a a a a a a T ，求n T .19．〔此题总分为8分〕如图, 四棱柱1111D C B A ABCD -的底面ABCD 是正方形,O 为底面中心,⊥O A 1平面ABCD 21==AA AB .(1)证明: ⊥C A 1平面D D BB 11;(2)(理科做)求平面1OCB 与平面D D BB 11的夹角θ的大小.1A(2) (文科做)求三棱柱111ABD A B D -的体积.20.〔此题总分为10分〕如图，点(1,2)A 是离心率为22的椭圆C ：12222=+b x a y (0)a b >>上的一点，斜率为2的直线BD 交椭圆C 于B ，D 两点，且A 、B 、D 三点互不重合． 〔1〕求椭圆C 的方程；〔2〕求证：直线AB ，AD 的斜率之和为定值．21．〔此题总分为10分〕函数.ln )(,21)(2x e x g x x f ==〔1〕设函数),()()(x g x f x F -=求)(x F 的单调区间；〔2〕假设存在常数,,m k 使得m kx x f +≥)(对R x ∈恒成立，且m kx x g +≤)(对),0(+∞∈x 恒成立，如此称直线m kx y +=为函数)(x f 与)(x g 的“分界限〞，试问：)(x f 与)(x g 是否存在“分界限〞？假设存在，求出“分界限〞的方程，假设不存在，请说明理由.请考生在第22、23二题中任选一题作答，如果多做，如此按所做的第一题记分. 22．〔此题总分为8分〕选修4—4：坐标系与参数方程在平面直角坐标系xoy中，以O为极点，x轴非负半轴为极轴建立坐标系，曲线C的极坐标方程为2sin4cosρθθ=，直线l的参数方程为〔t为参数〕，两曲线相交于,M N两点.〔1〕写出曲线C的直角坐标方程和直线l的普通方程；〔2〕假设(2,4)P--求.23．〔此题总分为8分〕选修4—5：不等式选讲函数()|1||1| f x x x=-++.〔1〕求不等式()3f x≥的解集；〔2〕假设关于x的不等式2()f x a a≥-在R上恒成立，求实数a的取值范围.2014高三数学10月考试评分细如此 一．选择题〔每一小题3分，共36分〕二．填空题〔每一小题3分，共12分〕 13. 1； 14.)2,2(- 15.3-； 16.4 三.解答题(本大题共6小题，共52分.)17.(8分) 【解析】2122cos 12)4(2cos 121cos )4(sin )(22++++-=+++=x x x x x f ππ=23)42sin(22++πx ………………………………… 2分 〔1〕)(x f 的最大值为，最小值为)(x f 的最小正周期为ππ==22T ………………5分〔2〕由题3()2f x ≥，∴23)42sin(2223≥++πx Z k k x k x ∈+≤≤-≥+∴,8380)42sin(πππππ……………………7分又x x ∴∈],,0[π 的取值范围是37[0,][,]88πππ………………………8分18. (8分)17.解：〔I 〕当1=n 时，411==S a ， ………………… 1分题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 CCACDDBCDBBA当2≥n 时，121+=-=-n S S a n n n ，………… 3分又1a 不适合上式， ∴⎩⎨⎧≥+==2,121,4n n n a n ………… 4分 〔II 〕∵541121⨯=a a ，………… 5分当()()⎪⎭⎫⎝⎛+-+=++=≥+32112121321211,21n n n n a a n n n 时，… 6分∴⎪⎭⎫ ⎝⎛+-+++-+-+⨯=321121...9171715121541n n T n⎪⎭⎫ ⎝⎛+-+=3215121201n ()3221203+-=n 。

2015-2016学年山西大学附中高三（上）10月月考数学试卷（理科）一.选择题（每小题3分，满分36分，每小题给出的四个选项中，只有一项是题目要求的）1．设U=A∪B={x∈N|0≤x≤10}，A∩∁U B={1，2，3，5，7，9}，则B的非空真子集的个数为（）A．5 B．30 C．31 D．322．已知角α的终边经过点（3a﹣9，a+2），且cosα≤0，sinα＞0，则a的取值范围是（）A．（﹣2，3）B． D．3．已知等比数列{a n}中，各项都是正数，且a1，，2a2成等差数列，则=（）A．1+B．1﹣C．3+2D．3﹣24．下列命题中的说法正确的是（）A．若向量∥，则存在唯一的实数λ使得B．命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1”C．命题“∃x0∈R，使得”的否定是：“∀x∈R，均有x2+x+1≥0”D．“a≠5且b≠﹣5”是“a+b≠0”的充分不必要条件5．设a，b∈R，则“a＞b”是“a|a|＞b|b|”的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分又不必要条件6．已知正四棱锥S﹣ABCD中，SA=2，那么当该棱锥的体积最大时，它的高为（）A．1 B．C．2 D．37．设a，b，c为三角形ABC三边，a≠1，b＜c，若log c+b a+log c﹣b a=2log c+b alog c﹣b a，则三角形ABC的形状为（）A．锐角三角形B．直角三角形C．钝角三角形D．无法确定8．Rt△ABC的角A，B，C所对的边分别是a，b，c（其中c为斜边），分别以a，b，c边所在的直线为旋转轴，将△ABC旋转一周得到的几何体的体积分别是V1，V2，V3，则（）A．V1+V2=V3B．C．D．9．执行如图所示的程序框图，则输出的结果为（）A．4 B．9 C．7 D．510．已知，是平面内互不相等的两个非零向量，且||=1，﹣与的夹角为150°，则||的取值范围是（）A．（0，] B． C．（0，2] D．11．已知点P为双曲线=1（a＞0，b＞0）右支上一点，F1，F2分别为双曲线的左右焦点，且|F 1F2|=，I为三角形PF1F2的内心，若S=S+λS△成立，则λ的值为（）A．B． C．D．12．已知函数y=f（x）是定义域为R的偶函数．当x≥0时，f（x）=，若关于x的方程52﹣（5a+6）f（x）+6a=0（a∈R），有且仅有6个不同实数根，则实数a的取值范围是（）A．0＜a＜1或a=B．0≤a≤1或a=C．0＜a≤1或a=D．1＜a≤或a=0二.填空题（每题4分，满分16分）13．设i是虚数单位，是复数Z的共轭复数，若，则= ．14．向曲线x2+y2=|x|+|y|所围成的区域内任投一点，这点正好落在y=1﹣x2与x轴所围成区域内的概率为．15．已知点A（﹣），在抛物线C：y2=2px（p＞0）的准线上，点M，N在抛物线C上，且位于x轴的两侧，O是坐标原点，若=3，则点A到动直线MN的最大距离为．16．函数y=（）|x﹣1|+4cos2x﹣2（﹣3≤x≤5），则此函数的所有零点之和等于．三.解答题（本大题5个小题，共48分，解答应写出文字说明，证明过程或演算步骤）17．在△ABC中，内角A、B、C的对边分别为a、b、c，已知a、b、c成等比数列，且cosB=．（Ⅰ）求+的值；（Ⅱ）设•=，求a、c的值．18．甲箱子里装有3个白球m个黑球，乙箱子里装有m个白球，2个黑球，在一次试验中，分别从这两个箱子里摸出一个球，若它们都是白球，则获奖（1）当获奖概率最大时，求m的值；（2）在（1）的条件下，班长用上述摸奖方法决定参加游戏的人数，班长有4次摸奖机会（有放回摸取），当班长中奖时已试验次数ξ即为参加游戏人数，如4次均未中奖，则ξ=0，求ξ的分布列和Eξ．19．如图，在多面体ABCDEF中，ABCD为菱形，∠ABC=60°，EC⊥面ABCD，FA⊥面ABCD，G为BF的中点，若EG∥面ABCD．（Ⅰ）求证：EG⊥面ABF；（Ⅱ）若AF=AB，求二面角B﹣EF﹣D的余弦值．20．已知椭圆的离心率为，其左、右焦点分别为F1，F2，点P （x0，y0）是坐标平面内一点，且（O为坐标原点）．（1）求椭圆C的方程；（2）过点且斜率为k的动直线l交椭圆于A、B两点，在y轴上是否存在定点M，使以AB为直径的圆恒过这个点？若存在，求出M的坐标，若不存在，说明理由．21．已知函数f（x）的定义域（0，+∞），若y=在（0，+∞）上为增函数，则称f（x）为“一阶比增函数”；若y=在（0，+∞）上为增函数，则称f（x）为“二阶比增函数”．把所有由“一阶比增函数”组成的集合记为A1，把所有由“二阶比增函数”组成的集合记为A2（1）已知函数f（x）=x3﹣2hx2﹣hx，若f（x）∈A1且f（x）∉A2，求实数h的取值范围（2）已知f（x）∈A2，且存在常数k，使得对任意的x∈（0，+∞），都有f（x）＜k，求k 的最小值．2015-2016学年山西大学附中高三（上）10月月考数学试卷（理科）参考答案与试题解析一.选择题（每小题3分，满分36分，每小题给出的四个选项中，只有一项是题目要求的）1．设U=A∪B={x∈N|0≤x≤10}，A∩∁U B={1，2，3，5，7，9}，则B的非空真子集的个数为（）A．5 B．30 C．31 D．32【考点】交、并、补集的混合运算；子集与真子集．【专题】计算题；转化思想；集合．【分析】根据已知，求出集合B，结合n元集合的非空真子集的个数为2n﹣2个，可得答案．【解答】解：∵U=A∪B={x∈N|0≤x≤10}={0，1，2，3，4，5，6，7，8，9，10}，A∩∁U B={1，2，3，5，7，9}，∴B={0，4，6，8，10}共5个元素，故B的非空真子集的个数为25﹣2=30个，故选：B．【点评】本题考查的知识点是集合的交集，并集，补集运算，难度不大，属于基础题．2．已知角α的终边经过点（3a﹣9，a+2），且cosα≤0，sinα＞0，则a的取值范围是（）A．（﹣2，3）B． D．【考点】任意角的三角函数的定义；三角函数值的符号．【专题】三角函数的求值．【分析】根据题意可得2kπ+≤α＜kπ+π，k∈z，故有 a+2＞0，且3a﹣9≤0，解不等式组求得a的取值范围．【解答】解：由题意可得2kπ+≤α＜kπ+π，k∈z，∴a+2＞0，且3a﹣9≤0，解得﹣2＜a≤3，故选C．【点评】本题考查任意角的三角函数的定义，根据三角函数值的符号判断角所在的象限，得到a+2＞0，且3a﹣9≤0，是解题的关键，属于基础题．3．已知等比数列{a n}中，各项都是正数，且a1，，2a2成等差数列，则=（）A．1+B．1﹣C．3+2D．3﹣2【考点】等差数列的性质；等比数列的性质．【专题】计算题．【分析】先根据等差中项的性质可知得2×（）=a1+2a2，进而利用通项公式表示出q2=1+2q，求得q，代入中即可求得答案．【解答】解：依题意可得2×（）=a1+2a2，即，a3=a1+2a2，整理得q2=1+2q，求得q=1±，∵各项都是正数∴q＞0，q=1+∴==3+2故选C【点评】本题主要考查了等差数列和等比数列的性质．考查了学生综合分析的能力和对基础知识的理解．4．下列命题中的说法正确的是（）A．若向量∥，则存在唯一的实数λ使得B．命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1”C．命题“∃x0∈R，使得”的否定是：“∀x∈R，均有x2+x+1≥0”D．“a≠5且b≠﹣5”是“a+b≠0”的充分不必要条件【考点】命题的真假判断与应用．【专题】探究型；转化思想；平面向量及应用；简易逻辑．【分析】根据向量共线的充要条件，可判断A；写出原命题的否命题，可判断B；写出原命题的否定，可判断C；根据充要条件可判断D．【解答】解： ==时，∥，但任意实数λ均有，≠， =时，∥，但任意实数λ均有，故A错误；命题“若x2=1，则x=1”的否命题为“若x2≠1，则x≠1”，故B错误；命题“∃x0∈R，使得”的否定是：“∀x∈R，均有x2+x+1≥0”，故C正确；a≠5且b≠﹣5推不出a+b≠0，例如：a=2，b=﹣2时a+b=0，a+b≠0推不出a≠5且b≠﹣5，例如：a=5，b=﹣6，故“a≠5且b≠﹣5”是“a+b≠0”的既非充分条件也非必要条件，故D错误；故选：C【点评】本题以命题的真假判断与应用为载体考查了向量共线的充要条件，四种命题，特称命题的否定，充要条件等知识点，难度中档．5．设a，b∈R，则“a＞b”是“a|a|＞b|b|”的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分又不必要条件【考点】必要条件、充分条件与充要条件的判断．【专题】简易逻辑．【分析】根据不等式的性质，结合充分条件和必要条件的定义进行判断即可得到结论．【解答】解：若a＞b，①a＞b≥0，不等式a|a|＞b|b|等价为a•a＞b•b，此时成立．②0＞a＞b，不等式a|a|＞b|b|等价为﹣a•a＞﹣b•b，即a2＜b2，此时成立．③a≥0＞b，不等式a|a|＞b|b|等价为a•a＞﹣b•b，即a2＞﹣b2，此时成立，即充分性成立．若a|a|＞b|b|，①当a＞0，b＞0时，a|a|＞b|b|去掉绝对值得，（a﹣b）（a+b）＞0，因为a+b＞0，所以a﹣b＞0，即a＞b．②当a＞0，b＜0时，a＞b．③当a＜0，b＜0时，a|a|＞b|b|去掉绝对值得，（a﹣b）（a+b）＜0，因为a+b＜0，所以a﹣b＞0，即a＞b．即必要性成立，综上“a＞b”是“a|a|＞b|b|”的充要条件，故选：C．【点评】本题主要考查充分条件和必要条件的判断，利用不等式的性质结合分类讨论是解决本题的关键．6．已知正四棱锥S﹣ABCD中，SA=2，那么当该棱锥的体积最大时，它的高为（）A．1 B．C．2 D．3【考点】棱柱、棱锥、棱台的体积．【专题】计算题；压轴题．【分析】设出底面边长，求出正四棱锥的高，写出体积表达式，利用求导求得最大值时，高的值．【解答】解：设底面边长为a，则高h==，所以体积V=a2h=，设y=12a4﹣a6，则y′=48a3﹣3a5，当y取最值时，y′=48a3﹣3a5=0，解得a=0或a=4时，当a=4时，体积最大，此时h==2，故选C．【点评】本试题主要考查椎体的体积，考查高次函数的最值问题的求法．是中档题．7．设a，b，c为三角形ABC三边，a≠1，b＜c，若log c+b a+log c﹣b a=2log c+b alog c﹣b a，则三角形ABC的形状为（）A．锐角三角形B．直角三角形C．钝角三角形D．无法确定【考点】三角形的形状判断．【专题】转化思想；转化法；函数的性质及应用；解三角形．【分析】结合对数的运算性质，及换底公式的推论，可将已知化为：c2﹣b2=a2，再由勾股定理判断出三角形的形状．【解答】解：∵log c+b a+log c﹣b a=2log c+b alog c﹣b a，∴+=2，即log a（c﹣b）+log a（c+b）=2，∴log a（c2﹣b2）=2，即c2﹣b2=a2，故三角形ABC的形状为直角三角形，故选：B．【点评】本题考查的知识点是三角形形状判断，对数的运算性质，难度中档．8．Rt△ABC的角A，B，C所对的边分别是a，b，c（其中c为斜边），分别以a，b，c边所在的直线为旋转轴，将△ABC旋转一周得到的几何体的体积分别是V1，V2，V3，则（）A．V1+V2=V3B．C．D．【考点】棱柱、棱锥、棱台的体积；旋转体（圆柱、圆锥、圆台）．【专题】计算题；函数思想；转化思想；空间位置关系与距离．【分析】利用直角三角形的三边分别为a、b、c，a2+b2=c2，c为斜边，分别求得V1、V2、V3的值，可得结论．【解答】解：因为直角三角形的三边分别为a、b、c，a2+b2=c2，即c为斜边，则以边c所在直线为轴，将三角形旋转一周所得旋转体的体积为V3，则V3 =π（）2•c=πa2•b2•，以边a所在直线为轴，将三角形旋转一周所得旋转体的体积为V1，则V1=πb2•a，以边b所在直线为轴，将三角形旋转一周所得旋转体的体积为V2，则V2=πa2•b，∴，故选：D．【点评】本题考查几何体的体积的求法与大小关系，考查计算能力，属于中档题．9．执行如图所示的程序框图，则输出的结果为（）A．4 B．9 C．7 D．5【考点】程序框图．【专题】算法和程序框图．【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量n的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【解答】解：当n=1时，执行循环体后，T=2，S=18，n=3，不满足退出循环的条件，当n=3时，执行循环体后，T=8，S=36，n=5，不满足退出循环的条件，当n=5时，执行循环体后，T=32，S=54，n=7，不满足退出循环的条件，当n=7时，执行循环体后，T=128，S=72，n=9，满足退出循环的条件，故输出的n值为9，故选：B【点评】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．10．已知，是平面内互不相等的两个非零向量，且||=1，﹣与的夹角为150°，则||的取值范围是（）A．（0，] B． C．（0，2] D．【考点】数量积表示两个向量的夹角．【专题】综合题；运动思想；数形结合法；平面向量及应用．【分析】如图所示，设，，则=．由于||=1，﹣与的夹角为150°，可得△OAB中，OA=1，∠OBA=30°．由正弦定理可得：△OAB的外接圆的半径r=1．则点B为圆上的动点．由图可令=（1+cosθ，sinθ），则||的取值范围可求．【解答】解：如图所示，设，，则=．由于||=1，﹣与的夹角为150°，可得△OAB中，OA=1，∠OBA=30°．由正弦定理可得：△OAB的外接圆的半径r=1．则点B为圆上的动点．由图可令=（1+cosθ，sinθ），则=．∴．故选：C．【点评】本题考查了数量积运算性质、三角函数的单调性、正弦定理、三角形外接圆的性质，考查了数形结合的能力、推理能力与计算能力，属于有一定难题题目．11．已知点P为双曲线=1（a＞0，b＞0）右支上一点，F1，F2分别为双曲线的左右焦点，且|F1F2|=，I为三角形PF1F2的内心，若S=S+λS△成立，则λ的值为（）A．B． C．D．【考点】双曲线的简单性质．【专题】圆锥曲线的定义、性质与方程．【分析】设△PF1F2的内切圆半径为r，由|PF1|﹣|PF2|=2a，|F1F2|=2c，用△PF1F2的边长和r 表示出等式中的三角形的面积，解此等式求出λ．【解答】解：设△PF1F2的内切圆半径为r，由双曲线的定义得|PF1|﹣|PF2|=2a，|F1F2|=2c，S△IPF1 =|PF1|•r，S△IPF2=|PF2|•r，S△IF1F2=•2c•r=cr，由题意得： |PF1|•r=|PF2|•r+λcr，故λ==，∵|F1F2|=，∴=∴∴=故选D．【点评】本题考查双曲线的定义和简单性质，考查三角形面积的计算，考查利用待定系数法求出参数的值．12．已知函数y=f（x）是定义域为R的偶函数．当x≥0时，f（x）=，若关于x的方程52﹣（5a+6）f（x）+6a=0（a∈R），有且仅有6个不同实数根，则实数a的取值范围是（）A．0＜a＜1或a=B．0≤a≤1或a=C．0＜a≤1或a=D．1＜a≤或a=0【考点】函数奇偶性的性质；根的存在性及根的个数判断；分段函数的应用．【专题】数形结合；函数的性质及应用；三角函数的图像与性质．【分析】运用偶函数的定义可得f（x）在x＜0的解析式，作出函数f（x）的图象，由52﹣（5a+6）f（x）+6a=0，解得f（x）=a或f（x）=，结合图象，分析有且仅有6个不同实数根的a的情况，即可得到a的范围．【解答】解：函数y=f（x）是定义域为R的偶函数，当x≥0时，f（x）=，当x＜0时，f（x）=．作出函数f（x）的图象如右．由于关于x的方程52﹣（5a+6）f（x）+6a=0，解得f（x）=a或f（x）=，当0≤x≤1时，f（x）∈，x＞1时，f（x）∈（1，）．由1＜＜，则f（x）=有4个实根，由题意，只要f（x）=a有2个实根，则由图象可得当0＜a≤1时，f（x）=a有2个实根，当a=时，f（x）=a有2个实根．综上可得：0＜a≤1或a=．故选：C．【点评】本题考查函数的奇偶性和单调性的运用，考查方程和函数的转化思想，运用数形结合的思想方法是解决的常用方法．二.填空题（每题4分，满分16分）13．设i是虚数单位，是复数Z的共轭复数，若，则= ﹣1+i ．【考点】复数代数形式的乘除运算．【专题】转化思想；综合法；数系的扩充和复数．【分析】利用复数的运算法则、共轭复数的定义即可得出．【解答】解： ====﹣i﹣1，则=﹣1+i，故答案为：﹣1+i．【点评】本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．14．向曲线x2+y2=|x|+|y|所围成的区域内任投一点，这点正好落在y=1﹣x2与x轴所围成区域内的概率为．【考点】几何概型．【专题】计算题；数形结合；数形结合法；概率与统计．【分析】欲求所投的点落在阴影部分内部的概率，须结合定积分计算阴影部分平面区域的面积，再根据几何概型概率计算公式易求解．【解答】解：曲线x2+y2=|x|+|y|所围成的区域为分别以（，），（﹣，），（﹣，﹣），（，﹣），为圆心，以为半径的圆，如图所示的面积，其面积为4×π×﹣2（﹣1）=π+2，y=1﹣x2与x轴所围成区域S=（1﹣x2）dx=（x﹣x3）|=，故这点正好落在y=1﹣x2与x轴所围成区域内的概率为，故答案为：．【点评】本题考查几何概型的计算，涉及定积分在求面积中的应用，关键是正确计算出阴影部分的面积．15．已知点A（﹣），在抛物线C：y2=2px（p＞0）的准线上，点M，N在抛物线C上，且位于x轴的两侧，O是坐标原点，若=3，则点A到动直线MN的最大距离为．【考点】抛物线的简单性质．【专题】平面向量及应用；直线与圆；圆锥曲线的定义、性质与方程．【分析】求得抛物线的准线方程，由题意解得p=1，设直线方程和点的坐标，联立直线与抛物线的方程得到一个一元二次方程，再利用韦达定理及•=3，消元，最后可得定点D坐标，连接AD，当AD⊥MN，有点A到动直线MN的距离最大，由两点的距离公式计算即可得到．【解答】解：抛物线C：y2=2px（p＞0）的准线为x=﹣，由题意得﹣=﹣，解得p=1．即有抛物线方程为y2=2x，设直线MN的方程为：x=ty+m，点M（x1，y1），N（x2，y2），直线MN与x轴的交点为D（m，0），x=ty+m代入y2=2x，可得y2﹣2ty﹣2m=0，根据韦达定理有y1•y2=﹣2m，∵•=3，∴x1•x2+y1•y2=3，从而（y1•y2）2+y1•y2﹣3=0，∵点M，N位于x轴的两侧，∴y1•y2=﹣6，故m=3．当y=0时，x=3恒成立，故直线MN所过的定点坐标是D（3，0），当直线MN绕着定点D（3，0）旋转时，AD⊥MN，即有点A到动直线MN的距离最大，且为=．故答案为：．【点评】求解本题时，应考虑联立直线与抛物线的方程，消x或y后建立一元二次方程，利用韦达定理与已知条件消元，再由观察可得点到直线的距离的最大，这是处理此类问题的常见模式．16．函数y=（）|x﹣1|+4cos2x﹣2（﹣3≤x≤5），则此函数的所有零点之和等于8 ．【考点】函数零点的判定定理．【专题】计算题；作图题；函数的性质及应用．【分析】化简y=（）|x﹣1|+4cos2x﹣2=（）|x﹣1|+2cos（πx）；从而得到其图象关于x=1对称，再化函数的零点个数即y=（）|x﹣1|与y=﹣2cos（πx）的交点的个数，从而求到个数，从而解得．【解答】解：y=（）|x﹣1|+4cos2x﹣2=（）|x﹣1|+2cos（πx）；其图象关于x=1对称，此函数的零点个数即y=（）|x﹣1|与y=﹣2cos（πx）的交点的个数，作y=（）|x﹣1|与y=﹣2cos（πx）的图象如下，由图象可知，其共有8个零点，又由其图象关于x=1对称知，8个零点之和为8×1=8；故答案为：8．【点评】本题考查了函数的零点与方程的根的关系，属于中档题．三.解答题（本大题5个小题，共48分，解答应写出文字说明，证明过程或演算步骤）17．在△ABC中，内角A、B、C的对边分别为a、b、c，已知a、b、c成等比数列，且cosB=．（Ⅰ）求+的值；（Ⅱ）设•=，求a、c的值．【考点】平面向量数量积的运算；同角三角函数基本关系的运用．【专题】平面向量及应用．【分析】（Ⅰ）由cosB=，B∈（0，π）．可得．由a、b、c成等比数列，可得b2=ac，再利用正弦定理可得sinAsinC=sin2B．于是可得+===；（Ⅱ）设•=，则，可得ac=2．再利用余弦定理可得：b2=a2+c2﹣2accosB化简整理，联立即可得出．【解答】解：（Ⅰ）由cosB=，B∈（0，π）．∴=．∵a、b、c成等比数列，∴b2=ac，由正弦定理可得sinAsinC=sin2B．∴+=====；（Ⅱ）设•=，则，∴，化为ac=2．由余弦定理可得：2=ac=b2=a2+c2﹣2accosB=，化为a2+c2=5．联立，解得或．即a=2，c=1，或a=1，c=2．【点评】本题考查了等比数列的性质、正弦定理与余弦定理、同角三角函数基本关系式，考查了推理能力和计算能力，属于中档题．18．甲箱子里装有3个白球m个黑球，乙箱子里装有m个白球，2个黑球，在一次试验中，分别从这两个箱子里摸出一个球，若它们都是白球，则获奖（1）当获奖概率最大时，求m的值；（2）在（1）的条件下，班长用上述摸奖方法决定参加游戏的人数，班长有4次摸奖机会（有放回摸取），当班长中奖时已试验次数ξ即为参加游戏人数，如4次均未中奖，则ξ=0，求ξ的分布列和Eξ．【考点】离散型随机变量的期望与方差；离散型随机变量及其分布列．【专题】计算题；转化思想；综合法；概率与统计．【分析】（1）利用相互独立事件概率乘法公式能求出获奖概率，由此能求出获奖概率最大时，m的值．（2）由已知得ξ的取值为0，1，2，3，4，分别求出相应的概率，由此能求出ξ的分布列和数学期望．【解答】解：（1）∵甲箱子里装有3个白球m个黑球，乙箱子里装有m个白球，2个黑球，在一次试验中，分别从这两个箱子里摸出一个球，若它们都是白球，则获奖，∴获奖概率或3时，．（4分）（2）由已知得ξ的取值为0，1，2，3，4，P（ξ=0）=（1﹣）4=，P（ξ=1）=，P（ξ=2）==，P（ξ=3）=×=，P（ξ=4）==，∴ξ的分布列为：ξ 1 2 3 4 0P．（12分）【点评】本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，在历年高考中都是必考题型之一．19．如图，在多面体ABCDEF中，ABCD为菱形，∠ABC=60°，EC⊥面ABCD，FA⊥面ABCD，G为BF的中点，若EG∥面ABCD．（Ⅰ）求证：EG⊥面ABF；（Ⅱ）若AF=AB，求二面角B﹣EF﹣D的余弦值．【考点】用空间向量求平面间的夹角；直线与平面垂直的判定；二面角的平面角及求法．【专题】综合题．【分析】（Ⅰ）取AB的中点M，连接GM，MC，证明CE∥GM，可得EG∥面ABCD，从而EG∥CM，证明EG⊥AB，EG⊥AF，可得EG⊥面ABF．（Ⅱ）建立如图所示的坐标系，设AB=2，求出平面BEF的法向量=（，1，2），平面DEF 的法向量=（﹣，1，2），利用向量的夹角公式，即可求二面角B﹣EF﹣D的余弦值．【解答】（Ⅰ）证明：取AB的中点M，连接GM，MC，G为BF的中点，所以GM∥FA，又EC⊥面ABCD，FA⊥面ABCD，∴CE∥AF，∴CE∥GM，∵面CEGM∩面ABCD=CM，EG∥面ABCD，∴EG∥CM，∵在正三角形ABC中，CM⊥AB，又AF⊥CM∴EG⊥AB，EG⊥AF，∴EG⊥面ABF．（Ⅱ）解：建立如图所示的坐标系，设AB=2，则B（，0，0），E（0，1，1），F（0，﹣1，2）=（0，﹣2，1），=（，﹣1，﹣1），=（，1，1），设平面BEF的法向量=（x，y，z）则，∴可取=（，1，2）同理，可求平面DEF的法向量=（﹣，1，2）设所求二面角的平面角为θ，则cosθ=﹣．【点评】本题考查线面垂直，考查面面角，正确运用线面垂直的判定，求出平面的法向量作是解题的关键．20．已知椭圆的离心率为，其左、右焦点分别为F1，F2，点P （x0，y0）是坐标平面内一点，且（O为坐标原点）．（1）求椭圆C的方程；（2）过点且斜率为k的动直线l交椭圆于A、B两点，在y轴上是否存在定点M，使以AB为直径的圆恒过这个点？若存在，求出M的坐标，若不存在，说明理由．【考点】椭圆的简单性质；椭圆的标准方程；直线与圆锥曲线的综合问题．【专题】计算题；综合题；压轴题．【分析】（1）设出P的坐标，利用|OP|的值求得x0和y0的关系式，同时利用求得x0和y0的另一关系式，进而求得c，通过椭圆的离心率求得a，最后利用a，b和c的关系求得b，则椭圆的方程可得．（2）设出直线l的方程，与椭圆方程联立消去y，设A（x1，y1），B（x2，y2），则可利用韦达定理表示出x1+x2和x1x2，假设在y轴上存在定点M（0，m），满足题设，则可表示出，利用=0求得m的值．【解答】解：（1）设P（x0，y0），F1（﹣c，0），F2（c，0），则由；由得，即．所以c=1又因为．因此所求椭圆的方程为：．（2）动直线l的方程为：，由得．设A（x1，y1），B（x2，y2）．则．假设在y轴上存在定点M（0，m），满足题设，则．====由假设得对于任意的恒成立，即解得m=1．因此，在y轴上存在定点M，使得以AB为直径的圆恒过这个点，点M的坐标为（0，1）【点评】本题主要考查了椭圆的简单性质．考查了学生分析问题和推理的能力．21．已知函数f（x）的定义域（0，+∞），若y=在（0，+∞）上为增函数，则称f（x）为“一阶比增函数”；若y=在（0，+∞）上为增函数，则称f（x）为“二阶比增函数”．把所有由“一阶比增函数”组成的集合记为A1，把所有由“二阶比增函数”组成的集合记为A2（1）已知函数f（x）=x3﹣2hx2﹣hx，若f（x）∈A1且f（x）∉A2，求实数h的取值范围（2）已知f（x）∈A2，且存在常数k，使得对任意的x∈（0，+∞），都有f（x）＜k，求k 的最小值．【考点】函数与方程的综合运用．【专题】计算题；函数的性质及应用；导数的综合应用．【分析】（1）由f（x））∈A1且f（x）∉A2知g（x）==x2﹣2hx﹣h在（0，+∞）上为增函数，F（x）==x﹣﹣2h在（0，+∞）上不是增函数，求导F′（x）=1+；从而确定h的取值范围；（2）利用反证法先证明f（x）≤0对任意的x∈（0，+∞）成立，再证明f（x）=0在（0，+∞）上无解，从而可是当f（x）∈A2时，对任意的x∈（0，+∞），都有f（x）＜0成立，故当常数k≥0时，使得对任意的x∈（0，+∞），都有f（x）＜k；从而求最小值．【解答】解：（1）∵f（x））∈A1且f（x）∉A2，即g（x）==x2﹣2hx﹣h在（0，+∞）上为增函数，∴h≤0；而F（x）==x﹣﹣2h在（0，+∞）上不是增函数，且F′（x）=1+；当F（x）是增函数时，有h≥0；所以当F（x）不是增函数时，h＜0；综上，h＜0．（2）先证明f（x）≤0对任意的x∈（0，+∞）成立，假设存在x0∈（0，+∞），使得f（x0）＞0，记=m＞0，因为f（x）∈A2，所以f（x）为“二阶比增函数”，即是增函数，所以当x＞x0＞0时，＞=m，即f（x）＞mx2；所以一定存在x1＞x0＞0，使得f（x1）＞m＞k成立，这与f（x）＜k对任意的x∈（0，+∞）成立矛盾，所以f（x）≤0对任意的x∈（0，+∞）都成立；再证明f（x）=0在（0，+∞）上无解，假设存在x2＞0，使得f（x2）=0；∵f（x）为“二阶比增函数”，即是增函数，∴一定存在x3＞x2＞0，使得＞=0成立，这与上述的证明结果矛盾．所以f（x）=0在（0，+∞）上无解，综上所述，当f（x）∈A2时，对任意的x∈（0，+∞），都有f（x）＜0成立，所以当常数k≥0时，使得对任意的x∈（0，+∞），都有f（x）＜k；故k的最小值为0．【点评】本题考查了学生对新定义的接受与转化运用的能力，同时考查了导数的综合应用，属于难题．。