四川省成都市高新区高一数学10月月考试题

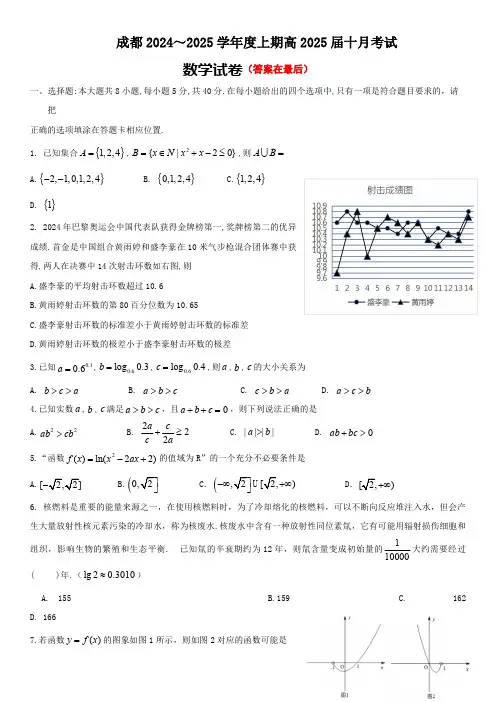
成都2024～2025学年度上期高2025届十月考试数学试卷（答案在最后）一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的，请把正确的选项填涂在答题卡相应位置.1.已知集合{}1,2,4A =,2{|20}B x N x x =∈+-≤,则A B = A.{}2,1,0,1,2,4-- B.{}0,1,2,4 C.{}1,2,4D.{}12.2024年巴黎奥运会中国代表队获得金牌榜第一,奖牌榜第二的优异成绩.首金是中国组合黄雨婷和盛李豪在10米气步枪混合团体赛中获得,两人在决赛中14次射击环数如右图,则A.盛李豪的平均射击环数超过10.6B.黄雨婷射击环数的第80百分位数为10.65C.盛李豪射击环数的标准差小于黄雨婷射击环数的标准差D.黄雨婷射击环数的极差小于盛李豪射击环数的极差3.已知0.10.6a =,0.6log 0.3b =,0.6log 0.4c =,则a ,b ,c 的大小关系为A.b c a>> B.a b c>> C.c b a>> D.a c b>>4.已知实数a ,b ,c 满足a b c >>，且0a b c ++=，则下列说法正确的是A.22ab cb > B.222a c c a+≥ C.||||a b > D.0ab bc +>5.“函数2()ln(22)f x x ax =-+的值域为R”的一个充分不必要条件是A.[2,2]- B.(0,2⎤⎦C．(,2[2,)⎤-∞+∞⎦U D．[2,)+∞6.核燃料是重要的能量来源之一，在使用核燃料时，为了冷却熔化的核燃料，可以不断向反应堆注入水，但会产生大量放射性核元素污染的冷却水，称为核废水.核废水中含有一种放射性同位素氚，它有可能用辐射损伤细胞和组织，影响生物的繁殖和生态平衡.已知氚的半衰期约为12年，则氚含量变成初始量的110000大约需要经过()年.（lg 20.3010≈）A.155 B.159C.162D.1667.若函数()y f x =的图象如图1所示，则如图2对应的函数可能是A.(12)y f x =-B.1(1)2y f x =-C.(12)y f x =-- D.1(1)2y f x =--8.已知函数11,0,()2221,0.x x x f x x ⎧+>⎪=⎨⎪-≤⎩,则方程()(3)2f x f x +-=的所有根之和为A．0B．3C．6D．9二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求。

四川省成都市高一上学期数学10月月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）已知全集U={1，2，3，4，5}，集合A={1，2}，B={2，3}，则（）A . {3}B . {4，5}C . {1，2，3}D . {2，3，4，5}2. （2分） (2016高一上·湖州期中) 函数y=loga（a﹣x）（a＞0且a≠1）的定义域为（）A . （﹣∞，a）B . （0，a）C . （a，+∞）D . （0，+∞）3. （2分）已知a＜，则化简的结果是（）A .B . -C .D . -4. （2分）下列函数中既是偶函数，又在区间上单调递增的函数是（）A .B .C .D .5. （2分）设函数若f（x）是奇函数，则g（2）的值是（）A . -B . -4C .D . 46. （2分） (2016高二下·黔南期末) 已知a是常数，函数的导函数y=f′（x）的图象如图所示，则函数g（x）=|ax﹣2|的图象可能是（）A .B .C .D .7. （2分）用分数指数幂表示（a＞0）其结果是（）A . aB .C .D .8. （2分）函数f（x）=ax2+2（a﹣1）x+2在区间（﹣∞，4]上为减函数，则a的取值范围为（）A . 0＜a≤B . 0≤a≤C . 0＜a＜D . a＞9. （2分） (2016高一上·东营期中) 当x∈[0，5]时，函数f（x）=3x2﹣4x+c的值域为（）A . [f（0），f（5）]B . [f（0），f（）]C . [c，f（5）]D . [f（），f（5）]10. （2分）已知函数（其中）的部分图象如图所示，为了得到g(x)=sin2x 的图象，则只需将f(x0的图象（）A . 向右平移个长度单位B . 向右平移个长度单位C . 向左平移个长度单位D . 向左平移个长度单位11. （2分）已知函数的图象上关于y轴对称的点至少有3对，则实数a 的取值范围是（）A . (0,)B . (,1)C . (,1)D . (0,)12. （2分）对于函数f（x）=-2x2+k，当实数k属于下列选项中的哪一个区间时，才能确保一定存在实数对a,b(a<b<0)，使得当函数f(x)的定义域为[a,b]时，其值域也恰好是[a,b]A . [-2,0)B .C .D .二、填空题 (共4题；共4分)13. （1分）已知函数f（x）=ax2+（b﹣3）x+3，x∈[2a﹣3，4﹣a]是偶函数，则a+b= ________14. （1分） (2017高三上·邳州开学考) 若函数f（x）= 是奇函数，那么实数a=________．15. （1分） (2016高一上·海安期中) 已知偶函数f（x）在[1，4]上是单调增函数，则f（﹣π）________ ．（填“＞”或“＜”或“=”）16. （1分） (2016高一上·清河期中) 定义在[﹣2，2]上的偶函数g（x），当x≥0时，g（x）单调递减，若g（1﹣m）﹣g（m）＜0，则实数m的取值范围是________．三、解答题 (共6题；共65分)17. （15分）(2019高一上·大庆期中) 已知集合，（1）求；（2）若，求的取值范围．18. （15分） a、b∈R+且a≠b， f（x）=|2x﹣1﹣1|．（1）比较c与1的大小；（2）比较的大小．19. （5分） (2019高一上·宜昌期中) 已知函数是定义在上的奇函数，且.（1）求实数的值；（2）用定义证明在上是增函数；（3）解关于的不等式 .20. （5分） (2017高一上·白山期末) 已知函数f（x）=lg（x2+tx+2）（t为常数，且﹣2 ＜t＜2 ）．（1）当x∈[0，2]时，求函数f（x）的最小值（用t表示）；（2）是否存在不同的实数a，b，使得f（a）=lga，f（b）=lgb，并且a，b∈（0，2）．若存在，求出实数t 的取值范围；若不存在，请说明理由．21. （10分） (2019高一上·延安期中) 已知函数的定义域为R，对定义域内任意的都有，且当时，有 .（1）求证：是奇函数；（2）求证：在定义域上单调递增；（3）求不等式的解集.22. （15分） (2017高一上·西城期中) 已知函数，．（1）当时，求函数的最大值和最小值．（2）求在区间上的最小值．参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共65分)17-1、17-2、18-1、18-2、19-1、19-2、19-3、20-1、20-2、21-1、21-2、21-3、22-1、22-2、。

高2016级第一期10月阶段性考试数学试题（考试时间：120分钟 满分：150分）一．选做题：（请从每个小题给出的A 、B 、C 、D 四个选项中选出唯一正确选项，每小题5分，12个小题共60分）1.已知全集{0,1,2,3,4}U =，集合{1,2,3}A =，{2,4}B =，则()U C A B =（ ）A ．{1,2,4}B ．{2,3,4}C ．{0,2,4}D ．{0,2,3,4} 2.已知函数()f x =） A ．{|2}x x ≥- B ．{|2}x x < C ．{|22}x x -<< D ．{|22}x x -≤<3.设函数()()()()10000x x f x x x π+>⎧⎪==⎨⎪<⎩，则(){}1f f f -=⎡⎤⎣⎦（ ）A.+1πB.0C.πD.-14. 若函数y ＝ax 与y ＝－bx在(0，＋∞)上都是减函数，则y ＝ax 2＋bx 在(0，＋∞)上是（ ）A ．减函数B ．增函数C ．先增后减D ．先减后增5.若不等式210x x a +++≥对一切102x ⎡⎤∈⎢⎥⎣⎦，都成立，则a 的最小值为（ ）.A 0.B 1-.C 52-.D 74-6.已知()f x 是定义在R 上的奇函数，若对任意的12,[0,)x x ∈+∞12x x ≠， 有2121()[()()]0x x f x f x -->，则（ ）A ．(3)(2)(1)f f f <-<B ．(1)(2)(3)f f f <-<C ．(2)(1)(3)f f f -<<D ．(3)(1)(2)f f f <<-7.甲、乙两人在一次赛跑中,路程s 与时间t 的函数关系如图所示,则下列说法正确的是 ( )A.甲比乙先出发B.乙比甲跑的路程多C.甲、乙两人速度相同D.甲先到达终点8．定义在()2,2-上的偶函数()f x ，当0x ≥时，()f x 为减函数，若()()1f m f m -<-，则实数m 的取值范围是（ ） A ．11,2⎛⎫- ⎪⎝⎭B ．1,2⎛⎫-∞ ⎪⎝⎭C ．1,22⎛⎫⎪⎝⎭D ．11,2⎡⎫-⎪⎢⎣⎭9. 若函数24()43x f x mx mx -=++的定义域为R ,则m 的取值范围是 （ ） A ．3[0,)4B ．03（，）4C ．3(,)4+∞D ．(,)-∞+∞10.在R 上定义运算⊗：(1)x y x y ⊗=-，若不等式1)()(<+⊗-a x a x 对任意实数x 成立，则实数a 的范围是（ ）.A 11<<-a .B 20<<a .C 2321<<-a .D 2123<<-a 11.若函数()()()2211,02,0b x b x f x x b x x -+->⎧⎪=⎨-+-≤⎪⎩，在R 上为增函数，则实数b 的取值范围是（ ）A ．1,2⎛⎫+∞⎪⎝⎭B ．(,2]-∞C ．1(,2]2D ．1(,2]212.已知函数1()1(0)f x x x=->,若存在正实数,()a b a b <,使()y f x =的定义域为(,)a b 时,值域为(,)ma mb ,则实数m 的取值范围是 ( )A.41<m B. 410<<m C. 41<m 且0≠m D. 41>m 二．填空题：（每小题5分，四个小题，共20分） 13.如图，集合U 为全集，A 、B 均是U 的子集， 图中阴影部分所表示的集合是14.已知函数)(x f y =在R 是奇函数，且当0≥x 时，x x x f 2)(2-=，则0<x 时,)(x f 的解析式为_______________15. 若集合{}{}|34,|211A x x B x m x m =-≤≤=-≤≤+，当B A A =时，则实数m 的取值范围是 。

四川省成都市2017-2018学年高一数学10月月考试题考试时间：120分钟满分：150分一.选择题.(本大题共12小题，每小题5分，共60分1.如果，则下列结论正确的是（）A. B. C. D.2. 下列函数中与图象相同的一个是（）A. B. C. D.3.定义在上的偶函数，对任意，，有，则有（）A. B.C. D.4.若奇函数在区间上为增函数，且有最小值0，则它在区间上（）A.是减函数，有最小值0B. 是增函数，有最小值0C.是减函数，有最大值0D. 是增函数，有最大值05. 设，则（）A． B． C． D．6. 若函数是R上的单调递增函数，则实数a的取值范围为A、 B、 C、 D、7.定义两种运算：，，则函数为（）A.奇函数B.偶函数C.既不是奇函数又不是偶函数D.既是奇函数又是偶函数8.若函数是定义域在上的偶函数，在上是减函数，且，则使的的取值范围为（）A. B. C. D.9.函数的图像是（）10.设是定义域在上的奇函数，，当时，，则的值为（）A. -0.5B. 0.5C. -5.5D. 7.511.已知函数，函数g(x)=b-f(2-x),其中b R,若f(x)-g(x)=0恰有4个解,则b的取值范围是( )A.( , )B.(- , )C.(0, ) D(,2)12. 定义在R上的函数，若关于的方程恰有5个不同的实数解，则=（）A．B．C．D．二．填空题.（本大题共4小题，每小题5分，共20分）13.已知，则的定义域为 .14.设函数为奇函数，则的值为 .15已知y=f(x)是定义在R上的奇函数,当x>0时,f(x)=- . 则f(x)解析式为 .16.关于函数，有下列四个结论：○1的值域为；○2是定义域上的增函数；○3对任意的，都有成立；○4与表示同一个函数.把你认为正确的结论的序号填写到横线上 .三．解答题.（本大题共6小题，其中17题10分，其余5个小题每题12分，共70分）17.已知集合.（1）若，求实数的值.（2）若，求实数的取值范围.18.（1）化简：（2）解不等式：19.（1）某工厂计划出售一种产品，经销人员并不是根据生产成本来确定这种产品的价格，而是通过对经营产品的零售商对于不同的价格情况下他们会进多少货进行调查.通过调查确定了关系式P=-750x+15000，其中P为零售商进货的数量，x为零售商愿意支付的每件价格。

一、单选题1．给出下列关系：①；；③；④；⑤，其中正确的个数πR ∈Q 3-∉Z |3|-∉N 0∉Q （ ） A ．1 B ．2C ．3D ．4【答案】A【分析】依次判断出各数所属于的数域范围，进而判断出正误.【详解】是实数，①②错误；是整数，③错误；是自然数，④π3-|3|3-=错误；0是有理数，⑤错误，所以正确的个数为1． 故选：A ．2．命题“”的否定为（ ）()10,,10x x∞∃∈++<A ．B ．()10,,10x x ∞∃∈++>()10,,10x x∞∃∈++≥C ．D ．()10,,10x x ∞∀∈++>()10,,10x x∞∀∈++≥【答案】D【分析】特称命题的否定：将存在改任意并否定原结论，即可得答案.【详解】由特称命题的否定为全称命题，则原命题的否定为.()10,,10x x ∞∀∈++≥故选：D3．已知集合，则（ ） {}024,{10}A x x B x x =≤-≤=->A B = A ．B ．{}2,1,0--{}2C ． D ． {21}xx -<∣…{12}xx <∣…【答案】C【分析】化简集合，然后利用交集的定义运算即得.【详解】因为， {}22,{1}A x x B x x =-≤≤=<∣∣所以. {21}A B xx ⋂=-<∣…故选：C.4．设集合，，则的真子集共有（ ）{}2340A x x x =--≤{}220,B x x x x =+>∈Z A B ⋂A ．15个 B ．16个 C ．31个 D ．32个【答案】A【分析】解一元二次不等式，求出，从而求出，得到的真子集个数.,A B A B ⋂A B ⋂【详解】由题意得，，{14}A x =-≤≤解得：或，所以或，220x x +>0x ><2x -{0B x x =>}2,Z x x <-∈所以，所以的子集共有个，真子集有15个． {1,2,3,4}A B ⋂=A B ⋂4216=故选：A ．5．“”是“”的（ ） 1x <21x <A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】B【分析】解不等式，利用集合的包含关系判断可得出合适的选项. 21x <【详解】由可得，因为 ， 21x <11x -<<{}<1x x {}1<<1x x -所以，“”是“”的必要不充分条件， 1x <21x <故选：D.6．若，则下列各式恒成立的是（ ） 13,24a b -<<<<A ． B ． 1214a b <-+<4211a b -<-+<-C ． D ．9211a b -<-+<-8210a b -<-+<【答案】D【分析】根据不等式的性质可得，进而即得. 8210a b -<-+<【详解】因为，24b <<所以，又， 824b -<-<-13a -<<则. 8210a b -<-+<故选：D.7．已知，则（ ） 22221,22P a b c Q a b c =+++=+A ． B ．C ．D ．的大小无法确定P Q …P Q =P Q …,P Q 【答案】C【分析】由题意，采用作差法，可得答案.【详解】，()()()22222221122110P Q a b c a b a b c c c ⎛⎫⎛⎫-=+++-+=-+-+-≥ ⎪ ⎪⎝⎭⎝⎭故，所以. 0P Q -≥P Q ≥故选：C.8．对任意的，恒成立，则的取值范围（ ）(,0)x ∈-∞210x mx -+>mA ．B ． {}22x x -<<{}2x x >C ．D ．{}2x x >-{}2x x ≤-【答案】C【分析】参变分离可得对任意的恒成立，利用基本不等式求出的最大值，1m x x >+(,0)x ∈-∞1x x +即可得解.【详解】解：因为对任意的，恒成立， (,0)x ∈-∞210x mx -+>即对任意的恒成立，21mx x <+(,0)x ∈-∞即对任意的恒成立，211x m x x x +>=+(,0)x ∈-∞因为，则，所以， (,0)x ∈-∞(0,)x -∈+∞()112x x x x ⎡⎤+=--+≤-=-⎢⎥-⎣⎦当且仅当，即时取等号， 1x x-=-=1x -所以. 2m >-故选：C二、多选题9．图中矩形表示集合，两个椭圆分别表示集合，则图中的阴影部分可以表示为( )U ,M NA ．B ． ()U M N ð()U N M ⋂ðC ．D ．()U M N M ⎡⎤⋂⋃⎣⎦ð()U M N M ⎡⎤⋃⋃⎣⎦ð【答案】AD【分析】分析图中阴影部分，结合集合交并补运算即可得到答案． 【详解】易知图中阴影部分为M 和的并集，故A 正确； U N ð又也可表示图中阴影部分，故D 也正确； ()U M N M ⎡⎤⋃⋃⎣⎦ð选项B ：表示的区域如图：()U N M ⋂ð选项C ：； ()U M N M U ⎡⎤⋂⋃=⎣⎦ð故AD 符合题意，BC 不符题意． 故选：AD ．10．如果，那么下列不等式一定成立的是（ ）0c b a >>>A ．B ． ()2c ab a b c +>+23a b b <C ． D ．2ab a -<-11a b>【答案】ABD【分析】通过已知中的，结合不等式的基本性质，逐一分析四个答案的正误，可得结0c b a >>>论.【详解】A 选项，，故A 成立；()()()2c ab a b c c a c b +-+=--B 选项，由，得，所以，根据不等式的性质，不等式两边同乘负数，得0a b <<a b >22a b >b ，故B 成立；23a b b <C 选项，由，根据不等式的性质，不等式两边同乘正数，得，即，故a b <a -2a ab -<-2ab a ->-C 不成立；D 选项，由，得，故D 成立. 0a b <<11a b>故选：ABD11．下列命题中为真命题的是( ) A ． 2,x x x ∃∈<R B ．2,0x x x ∀∈+>R C ．“”是“”的必要不充分条件 x ∈Q x ∈Z D ．“”的一个充分不必要条件可以是“" 2x >3x >【答案】ACD【分析】解出不等式即可判断AB ；根据整数和有理数的关系可判断C ；根据充分不必要条件的概念即可判断D 选项．【详解】对于选项A ，，故存在使得，故A 正确； 201x x x <⇒<<01x <<2x x <对于选项B ，或，即不等式的解不是，故B 错误；200x x x +>⇒>1x <-x ∈R 对于选项C ，，但，∴“”是“”的必要不充分条件，故C 正x ∈⇒Z x ∈Q x ∈Q ¿x ∈Z x ∈Q x ∈Z 确；对于选项D ，，但，∴“”的一个充分不必要条件可以是“”，故3x >⇒2x >2x >¿3x >2x >3x >D 正确． 故选：ACD ．12．下列命题正确的是（ ）A ．若，，则；0a b >>0m >+<+a a mb b m B ．若正数a 、b 满足，则； +=1a b 114113a b +≥++C ．若，则的最大值是；0x >423x x--2-D ．若，，，则的最小值是9； ()2x x y =-0x >0y >2x y +【答案】BC【分析】A 选项用作差法即可，B ，C ，D 选项都是利用基本不等式判断. 【详解】对于选项A ，，()()+=++a b ma a mb b m b b m --因为，，所以，0a b >>0m >0a b ->,即，故，所以A 错误；()()>0+a b m b b m -+>0+a a m b b m -+>+a a mb b m对于选项B ，因为，所以，+=1a b 113a b +++= ()111111114112113113113b a a b a b a b a b ++⎛⎫⎛⎫+=++++=++≥ ⎪ ⎪++++++⎝⎭⎝⎭当且仅当，即时，等号成立，故B 正确； 1111b a a b ++=++12a b ==对于选项C ，因为，即时，等号成立，所0x >43x x +≥=43x x =x =以C 正确； 4232x x--≤-对于选项D ，因为，所以， ()2x x y =-121y x+=所以，当且仅当即时，等号()1242248x y x y x y y x y x ⎛⎫+=++=+≥= ⎪⎝⎭4x y y x =4,2x y ==成立，所以的最小值是8，故D 错误.2x y +故选：BC.三、填空题13．已知，，则与的大小关系为__________． 23M x =-25N x =-M N 【答案】## M N >N M <【分析】利用作差法判断即可.【详解】解：因为，，23M x =-25N x =-所以， ()()22232522110M N x x x x x -=---=-+=-+>所以. M N >故答案为：M N >14．设集合，，若，则的取值范围是________． {|12}A x x =-<…{|}B x x a =<A B ⋂≠∅a 【答案】1a >-【解析】由集合间的关系，即可得出结论.【详解】因为，， {|12}A x x =-≤<{|}B x x a =<A B ⋂≠∅所以 1a >-故答案为：1a >-【点睛】本题考查的是集合的运算，较简单.15．给定集合AB ，定义：或，且，又已知，*{A B xx A =∈∣x B ∈ }x A B ∉ {0,1,2}A =，用列举法写出___________{1,2,3,4}B =*A B =【答案】{}0,3,4【分析】根据的定义直接求解即可. *A B 【详解】因为，{}0,1,2,3,4A B = {}1,2A B ={}*0,3,4A B ∴=故答案为：{}0,3,416．命题“，使”是假命题，则实数的取值范围为 _____．0x ∃∈R ()20030-++≤mx m x m m 【答案】()3,+∞【分析】直接利用特称命题和全称命题的转换和二次函数的性质的应用求出结果．【详解】命题“，使”是假命题，0x ∃∈R ()20030-++≤mx m x m则命题，恒成立为真命题，x ∀∈R ()230-++>mx m x m 所以当时，，不恒成立，0m =30x ->当时，需满足可得， 0m ≠0Δ0m >⎧⎨<⎩()22340m m m >⎧⎪⎨+-<⎪⎩解得， ()3,m ∈+∞故的范围为． m ()3,+∞故答案为：．()3,+∞四、解答题17．已知集合. {}{},2,3,1,3A x B x =-=-(1)若，写出的所有子集； 0x =A (2)若，求.B A ⊆A B ⋃【答案】(1)所有子集为：{}{}{}{}{}{}{},0,2,3,0,2,0,3,2,3,0,2,3∅----(2)12,,32⎧⎫-⎨⎬⎩⎭【分析】（1）根据子集的知识写出集合的所有子集. A （2）根据进行分类讨论，求得，进而求得. B A ⊆x A B ⋃【详解】（1）当时，，0x ={}0,2,3A =-所以的所有子集为： A {}{}{}{}{}{}{},0,2,3,0,2,0,3,2,3,0,2,3∅----（2）当时，， 1x x =-12x =此时，所以.11,2,3,,322A B ⎧⎫⎧⎫=-=⎨⎬⎨⎬⎩⎭⎩⎭12,,32A B ⎧⎫⋃=-⎨⎬⎩⎭当时，，21x -=-3x =经检验集合不满足集合的互异性，不符合题意.A 综上，.12,,32A B ⎧⎫⋃=-⎨⎬⎩⎭18．在①；②“”是“”的充分条件：③“”是“”的必要条件，在A B B ⋃=x A ∈x B ∈R x A ∈ðR x B ∈ð这三个条件中任选一个，补充到本题第（2）问的横线处，求解下列问题．问题：已知集合，． {2}A xa x a =+∣……{(1)(3)0}B x x x =+-<∣(1)当时，求；2a =A B ⋂(2)若________，求实数的取值范围．a 注：如果选择多个条件分别解答，按第一个解答计分． 【答案】(1) {}|2x x ≤<3(2) ()1,1-【分析】（1）首先解一元二次不等式得到集合，再求出集合，最后根据交集的定义计算可得； B A （2）根据所选条件均可得到，即可得到不等式，解得即可；A B ⊆【详解】（1）解：由，解得，所以(1)(3)0x x +-<13x -<<{}{|(1)(3)0}|13B x x x x x =+-<=-<<，当时，，所以2a ={|24}A x x =≤≤{}|23A B x x =≤< （2）解：若选①，则，所以，解得，即；A B B ⋃=A B ⊆123a a >-⎧⎨+<⎩11a -<<()1,1a ∈-若选②“”是“”的充分条件，所以，所以，解得，即x A ∈x B ∈A B ⊆123a a >-⎧⎨+<⎩11a -<<()1,1a ∈-；若选③“”是“”的必要条件，所以，所以，解得，即R x A ∈ðR x B ∈ðA B ⊆123a a >-⎧⎨+<⎩11a -<<；()1,1a ∈-19．已知a ＋b ≠0，证明a 2＋b 2－a －b ＋2ab ＝0成立的充要条件是a ＋b ＝1. 【答案】证明见解析.【分析】由a ＋b ＝1结合完全平方和公式证明充分性，利用完全平方和公式，提公因式对a 2＋b 2－a －b ＋2ab ＝0进行变形，结合a ＋b ≠0证明必要性. 【详解】证明：先证充分性： 若a ＋b ＝1则a 2＋b 2－a －b ＋2ab ＝(a ＋b )2－(a ＋b )＝1－1＝0，即充分性成立． 必要性：若a 2＋b 2－a －b ＋2ab ＝0则(a ＋b )2－(a ＋b )＝(a ＋b )(a ＋b －1)＝0因为a ＋b ≠0，所以a ＋b －1＝0 即a ＋b ＝1，成立综上a 2＋b 2－a －b ＋2ab ＝0成立的充要条件是a ＋b ＝1. 【点睛】本题主要考查了充要条件的证明，属于中档题.20．做一个体积为， 高为米的无上边盖的长方体纸盒， 底面造价每平方米元，四周每348m 340平方米为元， 问长与宽取什么数值时用总造价最低， 最低是多少?50【答案】长与宽均为4米时总费用最少，最少为元． 3040【分析】设长方体底面的长为，宽为，可得，总造价为元，表示出，再由基本不a m b m 16b a=y y 等式即可得解．【详解】解：设长方体底面的长为，宽为，显然，则，故，总造价为a m b m ,0a b >348ab =16b a=元，y则，当且仅当，即4816235016403006403006403040y a a a a ⎛⎫⎛⎫=+⨯+⨯=++≥⨯= ⎪ ⎪⎝⎭⎝⎭16a a =4a b ==时等号成立，当底面的长与宽均为4米时总费用最少，最少为元．∴304021．甲、乙两位消费者同时两次购买同一种物品，分别采用两种不同的策略，甲的策略是不考虑物品价格的升降，每次购买这种物品的数量一定；乙的策略是不考虑物品价格的升降，每次购买这种物品所花的钱数一定.（1）若两次购买这种物品的价格分别为元，元，求甲两次购买这种物品平均价格和乙两次购买64这种物品平均价格分别为多少；（2）设两次购买这种物品的价格分别为元，元，问甲、乙谁的购物比较经济合算. a b (0,0)a b >>【答案】（1）5，；（2）乙的购物比较经济合算 . 245【分析】（1）首先设甲每次购买这种物品的数量为，乙每次购买这种物品所花的钱数为，再分m n 别计算甲、乙的平均价格即可.（2）首先分别算出甲、乙的平均价格，再作差比较即可.【详解】（1）设甲每次购买这种物品的数量为，乙每次购买这种物品所花的钱数为，m n所以甲两次购买这种物品平均价格为，，645m mm m +=+乙两次购买这种物品平均价格为，.224564nn n=+（2）设甲每次购买这种物品的数量为，乙每次购买这种物品所花的钱数为， m n 所以甲两次购买这种物品平均价格为，，2am bm a bm m ++=+乙两次购买这种物品平均价格为，22nabn n a b a b=++， 22222()42()022()2()2()a b ab a b ab a b ab a b a b a b a b a b ++-+---===≥++++所以乙的购物比较经济合算.22．已知：“实数满足”，“”. p a {}{}11x m x m x x a ≠+⊂∣∣…………:q x ∀∈(1)已知为假命题，为真命题，求实数的取值范围； 1,m p =q a (2)若是的充分不必要条件，求实数的取值范围. p q ⌝m 【答案】(1)； []0,2(2). {11}mm >∣【分析】（1）将代入，化简，然后根据为假命题，为真命题，列出不等式，即可得到结1m =p p q 果.（2）先根据条件化简得到，然后根据是的充分不必要条件，列出不等式，即可得到,p q q ⌝p q ⌝结果.【详解】（1）当时，若为真命题，则，即. 1m =p {}{}121x x x x a ≠≤≤⊂∣……2a >若为真命题，则当时，满足题意；当时，，解得，所以q 0a =0a ≠2Δ120a a a >⎧⎨=-≤⎩012a <….012a ……故若为假命题，为真命题，则实数的取值范围为.p q a []0,2（2）对，且由（1）知，对，则或.1:1m p m a ≥⎧⎨+≤⎩:012q a ……:0q a ⌝<12a >因为是的充分不必要条件，所以，解得.p q ⌝112m +>11m >故的取值范围是. m {11}m m ∣。

2024-2025学年四川省成都七中高一（上）月考数学试卷（10月份）一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知集合A ={1,2}，B ={1,3,4}，则A ∪B =( )A. {1}B. {1,3,4}C. {1,2}D. {1,2,3,4}2.已知0<x <3，0<y <5，则3x−2y 的取值范围是( )A. (−1,0)B. (−10,9)C. (0,4)D. (0,9)3.对于实数x ，“2+x 2−x ≥0”是“|x|≤2”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.下列命题中真命题的个数是( )①命题“∀x ∈R ，|x|+x 2≥0”的否定为“∃x ∈R ，|x|+x 2<0”；②“a 2+(b−1)2=0”是“a(b−1)=0”的充要条件；③集合A ={y|y = x 2+1}，B ={x|y = x 2+1}表示同一集合．A. 0B. 1C. 2D. 35.已知实数x ，y 满足4x 2+4xy +y +6=0，则y 的取值范围是( )A. {y|−3≤y ≤2}B. {y|−2≤y ≤3}C. {y|y ≤−2}∪{y|y ≥3}D. {y|y ≤−3}∪{y|y ≥2}6.已知正实数a ，b 满足2a +b =1，则5a +b a 2+ab 的最小值为( )A. 3B. 9C. 4D. 87.关于x 的不等式(ax−1)2<x 2恰有2个整数解，则实数a 的取值范围是( )A. (−32,−43]∪(43，32]B. (−32,−43]∪[43,32)C. [−32,−43)∪(43,32]D. [−32,−43)∪[43，32)8.已知函数f(x)={4x 2−2x +3,x ≤122x +1x ,x >12，设a ∈R ，若关于x 的不等式f(x)≥|x−a 2|在R 上恒成立，则a 的取值范围是( )A. [−398,478]B. [−4,478]C. [−4,4 3]D. [−398,4 3]二、多选题：本题共3小题，共18分。

2023-2024学年上期十月阶段检测高2023级数学试卷（答案在最后）（考试时间：120分钟，总分：150分）注意事项：01．答题前，考生务必将自己的姓名、准考证号填写在答题卡规定的位置上，或将条形码贴在答题卡规定的位置上．02．答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号．03．答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上．04．所有题目必须在答题卡上作答，在试题卷上答题无效．05．考试结束后，只将答题卡交回．一、单选题（本题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1.已知集合{}220A x x x =-=，则（）A.{}0A∈ B.2A∉ C.{}2A∈ D.0A∈【答案】D 【解析】【分析】先化简集合A ，根据元素与集合的关系可得答案.【详解】因为{}{}2200,2A x x x =-==，所以{}{}0,2,0,2A A A A ∈∈⊂⊂.故选：D.2.已知全集{}1,2,3,4,5,6,7U =，{}2,4,6A =，{}1,3,5B =，则U A B ⋂ð等于A.{}2,5 B.{}1,3,5C.{}2,4,5 D.{}2,4,6【答案】D 【解析】【详解】因为全集1234567{}U =，，，，，，，{246}A =，，，5{}13B =，，，所以{}2467U B =，，，ð，所以{}246U A B ⋂=，，ð．故选：D.3.已知命题:p x R ∀∈,210x x -+>，则p ⌝A.x ∃∈R ，210x x -+≤ B.x ∀∈R ，210x x -+≤C.x ∃∈R ，210x x -+> D.x ∀∈R ，210x x -+≥【答案】A 【解析】【分析】根据全称命题与特称命题互为否定的关系，即可求解，得到答案．【详解】由题意，根据全称命题与特称命题的关系，可得命题:p x R ∀∈,210x x -+>，则:p ⌝x ∃∈R ，210x x -+≤，故选A ．【点睛】本题主要考查了含有一个量词的否定，其中解答中熟记全称命题与特称性命题的关系是解答的关键，着重考查了推理与运算能力，属于基础题．4.若,,R a b c ∈，则下列命题正确的是（）A.若0ab ≠且a b <，则11a b> B.若01a <<，则2a a >C.若0a b <<，则22a b > D.若,a b >c d >，则ac bd >【答案】C 【解析】【分析】根据不等式的性质结合作差法判断求解；【详解】选项A ：令1,1,a b =-=11a b>不成立，选项错误；选项B ：当01a <<时，()210a a a a -=-<，选项错误；选项C ：0a b <<，()()22a b a b a b -=+-，因为00a b a b +-＜，＜，所以220a b -＞，即22a b >，选项正确；选项D ：12,a b =-=-，31c d ==，，ac bd >，不成立，选项错误；故选：C.5.对于实数x ，“202xx+≥-”是“2x ≤”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】根据两个不等式解集的包含关系，判定结论.【详解】不等式202xx +≥-的解集{}22A x x =-≤<，不等式2x ≤的解集{}22B x x =-≤≤，由AB ，所以“202xx+≥-”是“2x ≤”的充分不必要条件.故选：A6.设2x >，则函数4412y x x =-+-，的最小值为（）A.7B.8C.14D.15【答案】D 【解析】【分析】利用基本不等式求解.【详解】因为2x >，所以20x ->，所以()444142771522y x x x x =-+=-++=--≥，当且仅当()4422x x -=-，即3x =时等号成立，所以函数4412y x x =-+-的最小值为15，故选:D ．7.若不等式20ax bx c ++<的解集是{}23x x <<，则不等式20cx bx a ++>的解集为A.1132⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭，， B.1132⎛⎫ ⎪⎝⎭，C.1123⎛⎫-- ⎪⎝⎭，D.1123⎛⎫⎛⎫-∞--+∞ ⎪ ⎪⎝⎭⎝⎭，【答案】A 【解析】【分析】由题可得2,3为20ax bx c ++=的两根,利用韦达定理算出,,a b c 的关系式,再将,,a b c 换成同一参数再求20cx bx a ++>的根即可.【详解】因为不等式20ax bx c ++<的解集是{}23x x <<,故0a >且2,3为20ax bx c ++=的两根.根据韦达定理有235236bac a⎧-=+=⎪⎪⎨⎪=⨯=⎪⎩,故56b a c a =-⎧⎨=⎩,故20cx bx a ++>可写成2650ax ax a -+>,因为0a >所以26510(21)(31)0x x x x -+>⇒-->解得13x <或12x >,即x ∈1132⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭，，故选A.【点睛】二次不等式的解集的端点值为二次函数的零点,注意二次函数开口方向影响不等式的取值在区间内还是区间外.8.对于集合,M N ，定义{}|,M N x x M x N -=∈∉，()()M N M N N M ⊕=-- ，设9|,R 4A x x x ⎧⎫=≥-∈⎨⎬⎩⎭，{}|0,R B x x x =<∈，则A B ⊕=（）A.904,⎛⎫-⎪⎝⎭B.904,⎡⎫-⎪⎢⎣⎭C.[)4,,90⎛⎫-∞-⋃+∞ ⎪⎝⎭ D.()4,,90⎛⎤-∞-⋃+∞ ⎥⎝⎦【答案】C 【解析】【分析】根据题中集合新定义的特性结合集合的基本运算可求解出结果.【详解】集合9|,R 4A x x x ⎧⎫=≥-∈⎨⎬⎩⎭，{}|0,R B x x x =<∈，则R A ð9,R 4x x x ⎧⎫=<-∈⎨⎬⎩⎭，R B ð{}|0,R x x x =≥∈，由定义可得：{A B x x A -=∈且}x B A ∉=⋂R B ð{}[)|0,R 0,x x x ∞=≥∈=+，{B A x x B -=∈且}x A B ∉=⋂R A ð99,R ,44x x x ∞⎧⎫⎛⎫=<-∈=--⎨⎬ ⎪⎝⎭⎩⎭，所以()()[)9,0,4A B A B B A ∞∞⎛⎫⊕=--=--+ ⎪⎝⎭，选项ABD 错误，选项C 正确.故选：C ．二、多选题（本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．）9.若集合{}1A x x =≥，则满足B A ⊆的集合B 可以是（）A.{}2,3 B.{}2x x ≥ C.{}0,1,2 D.{}0x x ≥【答案】AB 【解析】【分析】根据子集的定义可得出结论.【详解】{}1A x x =≥ ，则{}2,3A ⊆，{}2x x A ≥⊆，{}0,1,2A ⊄，{}x x ≥A .故选：AB.10.下列命题是真命题的为（）A.2,10x R x ∀∈--<B.,,n Z m Z nm m∀∈∃∈=C.所有圆的圆心到其切线的距离都等于半径D.存在实数x ，使得213234x x =-+【答案】ABC 【解析】【分析】根据题意，依次分析各选项即可得答案.【详解】对于A ，2,0x R x ∀∈-≤，所以210x --<，故A 选项是真命题；对于B ，当0m =时，nm m =恒成立，故B 选项是真命题；对于C ，任何一个圆的圆心到切线的距离都等于半径，故C 选项是真命题.对于D ，因为()2223122-+=-+≥x x x ，所以21132324x x ≤<-+.故D 选项是假命题.故选：ABC.11.若a ，b 均为正数，且21a b +=，则下列结论正确的是（）A.ab 的最大值为19B.12a b+的最小值为9C.224a b +的最小值为12 D.()()221a b ++的最小值为4【答案】BC 【解析】【分析】根据基本不等式“1”的妙用与()0,02a ba b +≤>>逐项判断即可.【详解】因为a ，b 均为正数，且21a b +=，所以21a b +=≥，所以18ab ≤，当且仅当2a b =，即12a =，14b =时，等号成立，所以A 错误；()12122214592b a a b a b a b a b ⎛⎫+=++=+++≥+ ⎪⎝⎭，当且仅当22b a a b =，即13a b ==时，等号成立，所以B 正确；()()22222212422224a b a b ab a b a b +⎛⎫=+-≥+-= ⎪⎝+⎭，当且仅当2a b =，即12a =，14b =时，等号成立，所以C 正确；()()222122142a b a b +++⎛⎫≤= ⎪⎝+⎭+，当且仅当221a b +=+，即0a =，12b =时，等号成立，而a ，b 均为正数，故等号不成立，所以D 错误.故选：BC.12.若关于x 的不等式201(0)ax bx c a ≤++≤>的解集为{}12x x -≤≤，则32a b c ++的值可以是（）A.59B.34C.56D.2【答案】ABC 【解析】【分析】根据解集的形式先分析出20ax bx c ++≥解集为R ，210ax bx c ++-≤的解集为[1,2]-，得到a 的范围，将32a b c ++最终用含a 的式子表达出来即可得到答案.【详解】先考虑20(0)ax bx c a ++≥>的解集，若解集不是R ，不妨设20ax bx c ++=的根为3434,()x x x x <，则20ax bx c ++≥的解集为(][)34,,x x -∞⋃+∞，根据最终解集的形式为[1,2]-可知：210ax bx c ++-≤的解集非空，设210ax bx c ++-=的根为1212,()x x x x <，则210ax bx c ++-≤的解集为12[,]x x ，由根与系数的关系：1234bx x x x a+=+=-，可能1234,,,x x x x 的排序有两种可能：3124x x x x <<<，此时原不等式201(0)ax bx c a ≤++≤>解集为空集，不符题意；又或者1342x x x x <<<，此时不等式的解集为1342[,][,]x x x x ⋃，形式与题意不符，于是原假设矛盾，故20(0)ax bx c a ++≥>的解集是R ，于是210ax bx c ++-≤的解集是[1,2]-，由韦达定理：12112b a c a ⎧-+=-⎪⎪⎨-⎪-⋅=⎪⎩，整理可得21b a c a =-⎧⎨=-+⎩，于是321a b c a ++=-+，又20(0)ax bx c a ++≥>解集是R ，故224()4(21)0b ac a a a ∆=-=--⋅-+≤，即2940a a -≤，结合题干0a >，于是409a <≤，故5321,19abc a ⎡⎫++=-+∈⎪⎢⎣⎭.故选：ABC三、填空题（本题共8小题，每小题5分，共计40分．）13.已知集合{1,2}A =-，2{,}B a a =，若{}1A B ⋂=，则实数a 的值为___【答案】1-【解析】【分析】由集合中元素的互异性以及集合间的运算即可求得.【详解】解：∵{1,2}A =-，2{,}B a a =，{}1A B ⋂=，∴21a =，且1a ≠，∴1a =-．故答案为：1-．14.已知32a b -≤<≤，则b a -的范围是______．【答案】05b a <-≤【解析】【分析】根据不等式的性质即可求解.【详解】由32a b -≤<≤可得32,32a b -≤<-<≤，0b a <-所以23a -<-≤，则05b a <-≤，故答案为：05b a <-≤15.中国健儿在杭州亚运会上取得傲人佳绩，获奖多多，为丰富学生课余生活，拓宽学生视野，石室成飞中学积极开展社团活动，每人都至少报名参加一个社团，高一（1）班参加A 杜团的学生有17人，参加B 杜团的学生有21人，参加C 社团的学生有22人，同时参加,A B 社团的学生有3人，同时参加,B C 社团的学生有4人，同时参加,A C 社团的学生有7人，三个社团同时参加的学生有1人，那么高一（1）班总共有学生人数为______．【答案】47【解析】【分析】根据题意，利用容斥原理结合集合的运算概念和运算方法，即可求解【详解】由题意，用,,A B C 分别表示参加A 杜团、参加B 杜团和参加C 杜团的学生形成的集合，则card()17,card()21,card()22A B C ===,card()3,card()4,card()7,card()1A B B C A C A B C ==== ,因此()()()()card card card card A B C A B C =++ ()()()()card card card card A B B C A C A B C ---+ 172122347147=++---+=.所以高一（1）班总共有学生人数为47人.故答案为：47.16.已知a b >，关于x 的不等式240ax x b ++≥对于一切实数x 恒成立，又存在实数0x ，使得20040ax x b ++=成立，则22a b a b+-的最小值为____________.【答案】【解析】【分析】首先由不等式恒成立得到4ab ≥，再由存在成立问题，得到4ab ≤，从而确定4ab =，然后将原问题转化为单变量最值问题，利用整体代换和基本不等式得到最值即可.【详解】由不等式240ax x b ++≥对于一切实数x 恒成立可得01640a ab >⎧⎨-≤⎩，解得4ab ≥，又存在实数0x ，使得20040ax x b ++=成立，则Δ1640ab =-≥，得4ab ≤，所以4ab =.∴4=b a∵a b>∴40a b a a-=->∴2222244848444a a a b a a a a b a a a a a a a ⎛⎫⎛⎫+-+ ⎪ ⎪+⎝⎭⎝⎭===-+≥----（当且仅当248a a ⎛⎫-= ⎪⎝⎭，4ab =，即a b ⎧=+⎪⎨=⎪⎩或a b ⎧=⎪⎨=⎪⎩取等号）故答案为：【点睛】本题的考查点较多，首先是对于能成立和恒成立问题的转化确定4ab =，然后运用了我们常用的一种处理最值的方法，多变量变单变量，最后在化解的过程中还需要整体代换，最后再利用基本不等式的方法求取最值，所以平时对于恒成立与能成立的问题要十分熟悉，最值问题的常见处理方法，如多变量多变单量法，整体代换法，构造一元二次不等式法，判别式法等，平时要熟练运用.四、解答题（本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤）17.已知U =R 且{}2560A x x x =--<，{}44B x x =-≤≤，求：（1）A B ⋃；（2）()()U UA B ⋂痧.【答案】（1）[)4,6-（2）()[),46,-∞-+∞ 【解析】【分析】（1）将集合A 化简，结合并集的运算，即可得到结果；（2）根据题意，由交集以及补集的运算，即可得到结果.【小问1详解】因为{}()25601,6A x x x =--<=-，且{}[]444,4B x x =-≤≤=-，则[)4,6A B =- .【小问2详解】由（1）可知，()[]1,6,4,4A B =-=-，则(][),16,U A =-∞-+∞U ð，()(),44,U B =-∞-+∞U ð，所以()()()[),46,U U A B ⋂=-∞-+∞U 痧.18.已知命题p ：x ∀∈R ，2240x tx -+≥恒成立，命题p 为真命题时实数t 的取值集合为A ．（1）求集合A ；（2）设集合{}231B t m t m =-<<+，若x B ∈是x A ∈的充分不必要条件，求实数m 的取值范围．【答案】（1）{}|22=-≤≤A t t （2）[)1,14,2⎡⎤+∞⎢⎥⎣⎦【解析】【分析】（1）根据一元二次不等式恒成立，0∆≤，求得结果即可.（2）根据充分不必要条件得出B 是A 的真子集，根据集合的包含关系列不等式求得结果.【小问1详解】命题p 为真命题时,x ∀∈R ，2240x tx -+≥恒成立，所以()22160∆=--≤t ，解得22t -≤≤，所以集合{}|22=-≤≤A t t .【小问2详解】若x B ∈是x A ∈的充分不必要条件，所以B 是A 的真子集，又{}231B t m t m =-<<+，当B =∅时，231m m -≥+，解得4m ≥，所以423212m m m <⎧⎪-≥-⎨⎪+≤⎩，解得112m ≤≤，所以实数m 的取值范围[)1,14,2⎡⎤+∞⎢⎥⎣⎦．19.为了减少能源损耗，房屋的屋顶和外墙通常需要建造隔热层，某地正在建设一座购物中心，现在计划对其建筑物建造可使用40年的隔热层，已知每厘米厚的隔热层建造成本为8万元．该建筑物每年的能源消耗费用P （单位：万元）与隔热层厚度x （单位：cm ）满足关系：()3R,0845mP x x x =∈≤≤+．若不建隔热层，每年能源消耗费用为9万元．设S 为隔热层建造费用与40年的能源消耗费用之和．（1）求m 的值及用x 表示S ；（2）当隔热层的厚度为多少时，总费用S 达到最小，并求最小值．【答案】（1）15m =，1800845S x x =++（08x ≤≤）；（2）当隔热层的厚度为6.25cm 时，总费用S 取得最小值110万元.【解析】【分析】（1）利用给定条件，求出m 的值，进而可得能源消耗费用与隔热层建造成本之和.（2）利用基本不等式即可求最值，根据等号成立的条件可得隔热层厚度.【小问1详解】设隔热层厚度x ，依题意，每年的能源消耗费用为：345m P x =+，而当0x =时，9P =，则395m =，解得15m =，显然建造费用为8x ，所以隔热层建造费用与40年的能源消耗费用之和为：45180040840884545S P x x x x x =+=⨯+=+++（08x ≤≤）.【小问2详解】由（1）知()180018008245104545S x x x x =+=++-++1026010110≥=⨯-=，当且仅当()180024545x x =++，即 6.25x =时取等号，所以当隔热层的厚度为6.25cm 时，总费用S 取得最小值110万元．20.（1）已知正实数x ，y 满足等式144x y +=，求4x y +的最小值；（2）已知0x >，0y >，228x y xy ++=，则2x y +的最小值．【答案】（1）4；（2）4.【解析】【分析】（1）利用“1”的妙用求出最小值作答；（2）利用均值不等式建立不等关系，再解一元二次不等式即可.【详解】（1）因为0,0x y >>，144x y+=，所以1114x y+=，所以()4441111244x y x y y x x y ⎛⎫+=+++≥+= +⎪⎝⎭，当且仅当44x y y x =即1,22x y ==时取等号，所以4x y +的最小值为4；（2）因为0,0,228x y x y xy >>++=，而()222222x y x y xy x y +⎛⎫++≤++ ⎪⎝⎭，当且仅当2x y =时取等号，因此()22282x y x y +⎛⎫++≥ ⎪⎝⎭，即()()2242320x y x y +++-≥，化为()()28240x y x y +++-≥，解得24x y +≥或28x y +≤-（舍去），由22820x y xy x y ++=⎧⎨=>⎩解得2,1x y ==，所以当2,1x y ==时，2x y +取得最小值4.21.已知关于x 的不等式()2121mx m x m m +-+-<-．（1）当2m =时，求该不等式的解集；（2）当R m ∈时，求该不等式的解集．【答案】（1）112x x ⎧⎫-<<⎨⎬⎩⎭（2）答案见解析【解析】【分析】（1）根据因式分解即可结合一元二次解的特征求解，（2）对m 分类讨论，即可结合一元二次不等式的解的特征求解.【小问1详解】当2m =时，2210x x --<，所以()121(1)012x x x +-<⇒-<<，故不等式的解为112x x ⎧⎫-<<⎨⎬⎩⎭【小问2详解】不等式()2121mx m x m m +-+-<-变形为()1(1)0mx x +-<，当0m =时，不等式为101x x -<⇒<，当0m >时，不等式可化为1(1)0x x m ⎛⎫+-< ⎪⎝⎭，解得11x m-<<，当10m -<<时，11m ->，不等式可化为1(1)0x x m ⎛⎫+-> ⎪⎝⎭，解得1x m >-或1x <，当1m <-时，11m -<，不等式可化为1(1)0x x m ⎛⎫+-> ⎪⎝⎭，解得1x m <-或1x >，当1m =-时，不等式可化为2(1)0x ->，解得1x ≠，综上可知：当0m =时，不等式的解为{}1x x <，当0m >时，不等式的解为11x x m ⎧⎫-<<⎨⎬⎩⎭，当10m -<<时，不等式的解为11x x x m ⎧⎫>-<⎨⎬⎩⎭或，当1m <-时，不等式的解为11x x x m ⎧⎫><-⎨⎩⎭或，当1m =-时，不等式的解为{}1x x ≠.22.已知二次函数22y ax bx =++(a ,b 为实数)且当1x =时，1y =．（1）当0a ≥时，对()2,5x ∀∈，0y >恒成立，求实数a 的取值范围；（2）对[]2,1a ∀∈--，0y >恒成立，求实数x 的取值范围．【答案】（1）(3)∞-+（2）11(,44+【解析】【分析】（1）依题意可得1b a =--，即对(2,5)x ∀∈，2(1)20ax a x -++>恒成立，参变分离可得2(1)x a x x ->-对(2,5)x ∀∈恒成立，令2t x =-，则212(1)3x x x t t-=-++，再利用基本不等式计算可得；（2）依题意2()20x x a x --+>对[]2,1a ∀∈--恒成立，结合一次函数的性质得到不等式组，解得即可；【小问1详解】1x = 时1y =，21a b ∴++=，即1b a =--，(2,5)x ∀∈ ，0y >恒成立，即2(1)20ax a x -++>恒成立，(1)2ax x x ∴->-恒成立，(2,5)x ∈ ，2(1)x a x x -∴>-，对(2,5)x ∀∈恒成立，max 2(1)x a x x ⎡⎤-∴>⎢⎥-⎣⎦．令2t x =-，则(0,3)t ∈，则22132(1)(2)(1)323x t t x x t t t t t t-===≤--++++++，当且仅当2t t=，即t =，此时2x =+时取“”=，所以实数a的取值范围时(3)∞-+．【小问2详解】[]2,1a ∀∈-- ，0y >恒成立，即2(1)20ax a x -++>对[]2,1a ∀∈--恒成立，2()20x x a x ∴--+>对[]2,1a ∀∈--恒成立．2222020x x x ⎧-++>∴⎨-+>⎩，解得11711744x x ⎧-+<<⎪⎨⎪<<⎩，1144x +∴<<，所以实数x的取值范围是11,44⎛+ ⎝⎭．。

成都外国语学校2016～2017学年上期高2016级高一10月月考数学试题满分：150分 时间：120分钟.第Ⅰ卷（60分）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的. 1.设全集{1,2,3,4,5}U =，集合{1,3,5}M =,{2,5}N =，则Venn 图中阴影部分表示的集合是（ ）A. {5}B. {1,3}C. {2,4}D. {2,3,4} 2. 已知:f A B →为从集合A 到集合B 的一个映射，{(,)|,},:(,)(,)A B x y x R y R f x y x y x y ==∈∈→+-,若A 中元素(1,)a 的象是(,4)b ，则实数,a b 的值分别为( )A. 2,3-B. 2,3--C. 3,2--D. 1,43．若函数()|1|||f x x x a =---是奇函数而不是偶函数，且()f x 不恒为0，则2016(1)a +的值（ ）A. 0B. 1C. 20162D. 201634. 已知21,(0)()(1)1,(0)x x f x f x x ⎧->=⎨+-≤⎩，则(1)f -=( )A.2-B. 1-C. 0D. 15. 设全集{|||4}U x Z x =∈<，集合{2,1,3}S =-，若U C P S ⊆，则这样的集合P 的个数共有( )A ．5B ．6C ．7D ．8 6.若集合2{|210}A x kx x =--=的元素至多一个，则实数k 的取值集合为（ ）A. 1k ≤-B.1k ≤-或者0k =C.(,1){0}-∞-UD. (,1]{0}-∞-U7．已知函数21(2016)(0)2x f x x x++=>，则函数()f x 的最小值是（ ） A. 2 B.2016 C.2015- D. 1 8. 下列五种说法正确的个数有（ ）①若,,A B C 为三个集合，满足A B B C =U I ，则一定有A C ⊆； ②函数的图像与垂直于x 轴的直线的交点有且仅有一个； ③若,A U B U ⊆⊆,则()()U A A B A C B =I U I ；④若函数()f x 在[,]a b 和[,]b c 都为增函数，则()f x 在[,]a c 为增函数.A. 1个B. 2个C. 3 个D. 4个9. 偶函数()()f x x R ∈满足：(4)(2)0f f -==，且在区间[0,3]与),3[+∞上分别递减和递增，则不等式()0x f x ⋅<的解集为( )A ．(,4)(4,)-∞-+∞UB ．(,4)(2,0)(2,4)-∞--U UC ．(,4)(2,0)-∞--UD ． (4,2)(2,4)--U10. 已知函数24,3()2,232ax x f x ax x x +≥⎧⎪=+⎨<<⎪-⎩在区间(2,)+∞为减函数，则实数a 的取值范围（ ）A. 1a <-B. 10a -<<C. 112a -<≤-D. 213a -<≤- 11. 已知函数12||4-+=x y 的定义域为),](,[Z b a b a ∈，值域为0,1]，那么满足条件的整数对),(b a 共有 （ ） A. 3个 B. 5个 C. 7个 D. 8个 12.已知函数,x R ∈符号[]x 表示不超过x 的最大整数，若函数[]()x m f x x m-=-，其中m N *∈，则给出以下四个结论其中正确是（ ）A.函数()f x 在(1,)m ++∞上的值域为1(,1]2B. 函数()f x 的图像关于直线x m =对称C.函数()f x 在(,)m +∞是减函数D. 函数()f x 在(1,)m ++∞上的最小值为12第Ⅱ卷（90分）二、填空题：本大概题共4小题，每小题5分. 13.集合4{|,}1M a Z a N a*=∈∈-用列举法表示为_________. 14.若函数f 的定义域为[0,3]，则函数(1)y f x =-的定义域________. 15.已知函数()f x =)(x f 在区间(]1,0上是减函数，则实数a 的取值范围是_______________.16.设集合11[0,),[,1]22A B ==,函数1,(),22(1),x x A f x x x B⎧+∈⎪=⎨⎪-∈⎩若0(())f f x A ∈,则0x 的取值范围是_____________.三、解答题：解答应写出文字说明过程或演算步骤。

2023-2024学年度（上）阶段性考试（一）高2023级数学（答案在最后）一、选择题：本题共8小题，每小题5分，共40分，每小题只有一个选项符合题目要求．1.命题“x ∀∈R ，23210x x -+>”的否定是（）A.x ∀∈R ，23210x x -+>B.x ∃∈R ，23210x x -+≤C.x ∃∈R ，23210x x -+< D.x ∀∈R ，23210x x -+<【答案】B【解析】【分析】根据全称命题与存在性命题的关系，准确改写，即可求解.【详解】根据全称命题与存在性命题的关系，可得命题“x ∀∈R ，23210x x -+>”的否定为：“x ∃∈R ，23210x x -+≤”.故选：B.2.设集合{}1,2,3,45,7A =，，{}2,4,5,6B =，则A B = （）A.{}1,2,3,4,5,7B.{}2,4,5,6C.{}2,4,5 D.{}1,2,3,4,5,6,7【答案】C【解析】【分析】直接进行交集运算即可求解.【详解】因为集合{}1,2,3,45,7A =，，{}2,4,5,6B =，则{}2,4,5A B = ，故选：C.3.设全集U ＝R ，M ＝{2x x <-或}2x >，N ＝{}13x x ≤≤.如图所示，则阴影部分所表示的集合为（）A.{}21x x -≤<B.{}23x x -≤≤C.{2x x ≤或}3x >D.{}22x x -≤≤【答案】A【解析】【分析】先观察Venn 图，得出图中阴影部分表示的集合，再结合已知条件，即可求解.【详解】由图中阴影部分表示的集中的元素在集合R C N 中，又在集合R C M 中，即()R R C M C N ⋂，又由{|2M x x =<-或2,},{|13}x N x x >=≤≤，所以图中阴影部分表示的集合为(){|22}{|1R R C M C N x x x x ⋂=-≤≤⋂<或3}{|21}x x x >=-≤<，故选：A.【点睛】本题主要考查了Venn 图表达集合的关系及其运算，以及Venn 图的应用等基础知识，其中解答中观察Venn 图，得出图中阴影部分表示的集合()R R C M C N ⋂是解答的关键，着重考查了推理与运算能力，以及数形结合思想的应用，属于基础题.4.设集合{}13A x x =-≤≤，集合{}B x x a =≥，若A B ⊆，则a 的取值范围为（）A.3a ≥ B.13a -≤≤ C.1a ≥- D.1a ≤-【答案】D【解析】【分析】直接由A B ⊆求解即可.【详解】由A B ⊆可得1a ≤-.故选：D.5.已知实数a 、b 、c ，且a b >，则下列不等式正确的是()A.22a b > B.11a b < C.11a b +>- D.22ac bc >【答案】C【解析】【分析】利用特值可进行排除，由不等式性质可证明C 正确.【详解】若a ＝1，b ＝﹣1，则A ，B 错误，若c ＝0，则D 错误，∵a ＞b ，∴a +1＞a ＞b ＞b ﹣1，∴a +1＞b ﹣1，故C 正确，故选C ．【点睛】本题主要考查不等式与不等关系，在限定条件下，比较几个式子的大小，可用特殊值代入法，属于基础题．6.已知02x <<，则()224xx -的最大值为（）A.8B.16C.2D.4【答案】D【解析】【分析】根据基本不等式得到最值.【详解】因为02x <<，所以20x >，240x ->，故()222224442x x x x ⎛⎫+--≤= ⎪⎝⎭，当且仅当224x x =-，即x =故()224x x -的最大值为4.故选：D 7.:p “{}23x x x x ∈≤”是q ：“{}21x x x ∈-<”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B【解析】【分析】解不等式，并得到{}13x x <<是{}03x x ≤≤的真子集，从而求出答案.【详解】:p {}{}2303x x x x x ≤=≤≤，:q {}{}2113x x x x -<=<<，由于{}13x x <<是{}03x x ≤≤的真子集，所以:p “{}23x x x x ∈≤”是q ：“{}21x x x ∈-<”的必要不充分条件.故选：B8.若不等式222424mx mx x x +-<+的解集为R ，则实数m 的取值范围是（）A.22m -<≤ B.22m -<< C.2m <-或2m ≥ D.2m ≤【答案】A【解析】【分析】由题意可知，不等式()()222240m x m x -+--<的解集为R ，分20m -=、20m -≠两种情况讨论，在第一种情况下，直接验证即可；在第二种情况下，根据题意可得出关于实数m 的不等式组，综合可求得实数m 的取值范围.【详解】由222424mx mx x x +-<+可得()()222240m x m x -+--<，由题意可知，不等式()()222240m x m x -+--<的解集为R ，当20m -=时，即当2m =时，则有4<0-，合乎题意；当20m -≠时，则有()()()()220Δ421624220m m m m m -<⎧⎪⎨=-+-=-+<⎪⎩，解得22m -<<.综上所述，22m -<≤.故选：A.二、选择题：本题共4小题，每小题5分，共20分，每小题有多个选项符合题目要求．9.下列各题中给出的两个语句p 和q ，哪些p 是q 的充要条件．．．．（）A.p ：四边形是菱形，q ：四边形的对角线互相垂直且平分B.p a =，:0q a >C.222:p x y z xy yz xz ++=++，:q x y z==D.p ：关于x 的不等式20ax bx c ++≥的解集是{}()1212x x x x x x ≤≤<，:0p a <且24b ac>【答案】ACD【解析】【分析】根据充分条件、必要条件的判定方法，逐项判定，即可求解．【详解】对于A ，由四边形是菱形，则四边形的对角线互相垂直且平分，即充分性成立，反之，由四边形的对角线互相垂直且平分，则四边形是菱形，即必要性不成立，所以p 是q 的充分必要条件，故A 正确；对于Ba =，则0a ≥，即充分性不成立，反之，由0a >，则a =，即必要性成立，所以p 是q 的必要不充分条件，故B 错误；对于C ，由222x y z xy yz xz ++=++，则2220x y z xy yz xz ++---=，即2222222220x y z xy yz xz ++---=，即2222222220x xy y y yz z x xz z -++-++-+=，即()()()2220x y y z x z -+-+-=，解得x y z ==，即充分性成立，反之，由x y z ==，则222x y z xy yz xz ++=++，即必要性成立，所以p 是q 的充分必要条件，故C 正确；对于D ，在不等式20ax bx c ++≥中，由不等式的解集是{}()1212x x x x x x ≤≤<，则a<0且240b ac ∆=->，即24b ac >，即充分性成立，反之，由a<0且24b ac >，即0∆>，则存在12x x <，使得不等式的解集是{}12x x x x ≤≤，即必要性成立，所以p 是q 的充分必要条件，故D 正确．故选：ACD ．10.已知3y x x =+，下列关于y 的最小值的描述正确的是（）A.2x ≥时，y 的最小值是B.0x >时，y 的最小值是C.3x x=时，y 取得最小值 D.0x <时，y 没有最小值【答案】BD【解析】【分析】利用对勾函数的性质一一判定即可.【详解】由对勾函数的性质可知3y x x =+在(,-∞和)+∞上单调递增，在()和(上单调递减，函数在定义域上无最小值，也无最大值.对于A ，2x ≥时，此时函数单调递增，y 在2x =时取得最小值3.5，不是A 错误；对于B ，0x >时，3y x x =+≥，当且仅当x =B 正确；对于C ，3x x=时，即x =，此时函数取不到最小值，故C 错误；对于D ，0x <时，根据对勾函数的单调性和值域知y 没有最小值，显然正确.故选：BD.11.若实数a 、b 满足：1513a b a b ≤+≤⎧⎨-≤-≤⎩，则下列叙述正确的是（）A.a 的取值范围是04a ≤≤ B.b 的取值范围是13b -≤≤C.32a b -的范围是23210a b -≤-≤ D.32a b -的范围是63214a b -≤-≤【答案】ABC【解析】【分析】利用不等式的基本性质求出各选项中代数式的范围，即可得出合适的选项.【详解】因为实数a 、b 满足：1513a b a b ≤+≤⎧⎨-≤-≤⎩，由不等式的可加性可得028a ≤≤，解得04a ≤≤，A 对；由题意可得1531a b b a ≤+≤⎧⎨-≤-≤⎩，由不等式的可加性可得226b -≤≤，解得13b -≤≤，B 对；设()()()()32a b x a b y a b x y a x y b -=++-=++-，则32x y x y +=⎧⎨-=-⎩，解得1252x y ⎧=⎪⎪⎨⎪=⎪⎩，所以，()()153222a b a b a b -=++-，因为()()1152225515222a b a b ⎧≤+≤⎪⎪⎨⎪-≤-≤⎪⎩，由不等式的可加性可得23210a b -≤-≤，C 对D 错.故选：ABC.12.关于x 的不等式22210x x a -+-≤的解集，下列说法正确的是（）A.0a =时，解集为∅B.0a >时，解集为{}11x a x a -≤≤+C.0a ≠时，解集为{}11x a x a-≤≤+ D.1a <-时，原不等式在02x ≤≤时恒成立【答案】BD【解析】【分析】根据一元二次不等式的解法判断ABC ；利用二次函数的性质判断D.【详解】0a =时，不等式为2210x x -+≤，即()210x -≤，解得1x ≠，解集为{}|1x x ≠，故A 错误；不等式22210x x a -+-≤可化为()()1110x a a ---+≤⎡⎤⎡⎤⎣⎦⎣⎦，当0a >时，11a a -<+，不等式的解集为{}11x a x a -≤≤+，当0a <时，11a a ->+，不等式的解集为{}11x a x a +≤≤-，故B 正确，C 错误；令22()21f x x x a =-+-，对称轴为1x =，当02x ≤≤时，2max ()(0)(2)1f x f f a ===-，又1a <-时，2211(1)0a -<--=，所以2max ()10f x a =-<，即不等式22210x x a -+-≤在02x ≤≤时恒成立，故D 正确．故选：BD ．三、填空题：本题共4小题，每小题5分，共20分．13.已知集合{}{}21,,A B a a==，且A B A = ，则a 的值为_________．【答案】1-【解析】【分析】由A B A = 得A B ⊆，列式求解，然后检验元素的互异性.【详解】∵A B A = ，∴A B ⊆，又{}{}21,,A B a a==，∴1a =或21a =，解得1a =或1a =-，当1a =不满足元素的互异性，舍去，所以1a =-.故答案为：1-.14.已知二次函数2y ax bx c =++图象如图所示，则不等式26bx cx a -≤的解集为_________．【答案】{}|13x x ≤≤【解析】【分析】利用图象计算a b c 、、再结合一元二次不等式的解法计算即可.【详解】由题意可知4c =，且142420116404a c a b c b a b c c ⎧=-⎪=⎧⎪⎪-+=⇒=⎨⎨⎪⎪++==⎩⎪⎩，所以不等式226430bx cx a x x -≤⇔-+≤，计算可得不等式解集为{}|13x x ≤≤.故答案为：{}|13x x ≤≤.15.若正实数a 、b 满足3a b +=，则14a b +的最小值为______.【答案】3【解析】【分析】利用乘“1”法及基本不等式计算可得.【详解】解：因为正实数a 、b 满足3a b +=，所以()14114141553333a a b a b a b a b b ⎛⎛⎫⎛⎫+=++=++≥+= ⎪ ⎪ ⎝⎭⎝⎭⎝，当且仅当4b a a b =，则23b a a b =⎧⎨+=⎩，即1a =，2b =时取等号，即14a b +的最小值为3.故答案为：316.一物流公司要租地建造仓库储存货物，经市场调研发现：每月土地租用费用1y （万元）与仓库到车站的距离()km s 成反比；每月库存货物费用2y （万元）与s 成正比；且10km s =时，1y 和2y 分别为2万元和8万元．那么这家公司把仓库建在距离车站_________千米处，费用之和最小．【答案】5【解析】【分析】利用基本不等式计算即可.【详解】由题意可设21y ks m y s =⎧⎪⎨=⎪⎩，,0k m >，当10km s =时，1y 和2y 分别为2万元和8万元，所以80.8,2102010k m ===⨯=，故费用之和为200.8y s s=+，由基本不等式可知200.88y s s =+≥=，当且仅当200.8s s=，即5s =时取得最小值.故答案为：5四、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．17.求下列不等式的解集：（1）23100x x -->（2）130x --≤【答案】（1）{|2x x <-或5}x >（2）{}|24x x -≤≤【解析】【分析】（1）对原不等式因式分解，直接利用一元二次不等式的解集情况求解即可.（2）利用绝对值不等式的求解过程直接求解.【小问1详解】原不等式可化为(5)(2)0x x -+>⇒<2x -或5x >∴原不等式的解集为{}|25x x x <->或【小问2详解】 13x -≤，∴313x -≤-≤∴42x -≤-≤∴24x -≤≤∴原不等式的解集为{}|24x x -≤≤18.已知全集U =R ，集合()(){}120A x x x =+-≤，集合{}23B x a x a =≤≤+，求：（1）若()()U U B A ⊆痧，求a 的范围；（2）若A B ⋂=∅，求a 的范围．【答案】（1）112a -≤≤-（2）4a <-或1a >【解析】【分析】（1）求出集合A ，由()()UU B A ⊆痧得出A B ⊆，列出不等式求解即可；（2）因为A ≠∅，A B ⋂=∅，所以分B =∅和B ≠∅两种情况讨论．【小问1详解】集合A 化简得：{}1|2x x -≤≤，()()U U B A ⊆ 痧，A B ∴⊆，2132a a ≤-⎧∴⎨+≥⎩，解得：112a -≤≤-，【小问2详解】因为A ≠∅，A B ⋂=∅，所以下面分B =∅和B ≠∅两种情况讨论．①B =∅时，233a a a >+⇒>，②B ≠∅时，3a ≤，又有下面两种情况，（ⅰ）（如图）31322a a a ≤⎧⇒<≤⎨>⎩，（ⅱ）（如图）3431a a a ≤⎧⇒<-⎨+<-⎩，综上所述，4a <-或1a >.19.已知命题2:R,230p x x mx m ∀∈-->；命题2:R,410q x x mx ∃∈++<．（1）若命题p 为真命题，求实数m 的取值范围；（2）若命题p ⌝真且q ⌝假，求实数m 的取值范围．【答案】（1）30m -<<（2）{|3m m ≤-或1}2m >【解析】【分析】（1）根据题意得到Δ0<，求出答案；（2）先求出q 真时，实数m 的取值范围，进而得到p ⌝真且q ⌝假时，实数m 的取值范围.【小问1详解】因为命题2:R,230p x x mx m ∀∈-->为真命题．所以2230x mx m -->在R 上恒成立，则判别式()()2Δ2430m m =--⨯-<即()23030m m m m +<⇔+<，解得30m -<<．所以实数m 的取值范围为30m -<<【小问2详解】2:R,410q x x mx ∃∈++<为真，即关于x 的不等式2410x mx ++<有解，则()2Δ440m =->，解得：12m >或12m <-，由题意，p ⌝真，所以p 假，所以3m ≤-或0m ≥，q ⌝假，所以q 真，所以12m >或12m <-，p 假且q 真，所以实数m 的取值范围为{3m m ≤-或12m ⎫>⎬⎭20.已知0,0a b >>．（12a b +≥，当且仅当a b =时等号成立；（2）若1a b +=的最大值．【答案】（1）证明见解析（2【解析】【分析】（1）用分析法证明；（2x y ==，则22,a x b y ==，221x y +=，结合（1）即可证明.【小问1详解】2a b +≥，因为0,0a b >>，只要证：22222a b a b ++⎛⎫≥ ⎪⎝⎭只要证：()()a b a b a b ab+≥+=++2222222只要证：2220a b ab +-≥上式即：()20a b -≥，此不等式显然成立，当且仅当0a b -=，即a b =时，“=”号成立所以原不等式得证．【小问2详解】x y ==，则22,a x b y ==，221x y +=由（1x y x y ++≥⇒≥22所以：x y +≤2x y ==时等号成立即12a b ==时，+21.已知二次函数2y ax bx c =++的图象与x 轴的两个交点的横坐标分别为1-和3，且方程24ax bx c ++=的两根相等．（1）求二次函数的解析式；（2）求关于x 的不等式()213ax bx c m x m ++>-++的解集．【答案】（1）223y x x =-++；（2）答案见解析.【解析】【分析】（1）利用二次函数的两根式设解析式，再借助判别式求出二次项系数即可.（2）利用（1）的结论，分类解含参不等式即得.【小问1详解】依题意，设二次函数解析式为：()()()130y a x x a =+-≠，则2,3b a c a =-=-，方程24ax bx c ++=，即22340ax ax a ---=的两根相等，因此()()2Δ24340a a a =-⋅--=，即216160a a +=，而0a ≠，解得1a =-，所以二次函数的解析式为223y x x =-++.【小问2详解】不等式()213ax bx c m x m ++>-++，即()22313x x m x m -++>-++，整理得：()210x m x m -++<，于是()()10x m x --<，当1m =时，不等式无解；当1m <时，解得1m x <<；当1m >时，解得1x m <<，所以当1m =时，原不等式解集为空集；当1m <时，原不等式解集为{}|1x m x <<；当1m >时，原不等式解集为{}1|x x m <<.22.为了净化空气，某科研单位根据实验得出，在一定范围内，每喷洒1个单位的净化剂，空气中释放的浓度y （单位：毫克/立方米）随着时间x （单位：天）变化的关系如下：当04x ≤≤时，88y x=-；当410x <≤时，142y x =-．若多次喷洒，则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和．由实验知，当空气中净化剂的浓度不低于4（毫克/立方米）时，它才能起到净化空气的作用．（1）若一次喷洒4个单位的净化剂，则净化时间可达几天？（2）若第一次喷洒2个单位的净化剂，6天后再喷洒()14a a ≤≤个单位的净化剂，要使接下来的4天中能够持续有效净化，试求a 的最小值．【答案】（1）6；（2）258．【解析】【分析】（1）解出不等式44y ≥即可；（2）设从第一次喷洒起，经()610x x ≤≤天，浓度8()14614a g x x x=-+--，然后利用基本不等式求出min ()6g x =，然后解出不等式64-≥即可.【详解】（1）因为一次喷洒4个单位的去污剂，所以空气中释放的浓度为，32,0448162,410x y x x x ⎧≤≤⎪=-⎨⎪-<≤⎩当04x ≤≤时，令3248x≥-，解得0x ≥，所以04x ≤≤；当410x <≤时，令1624x -≥，解得6x ≤，所以46x <≤．综上，可得06x ≤≤，即一次投放4个单位的去污剂，有效去污时间可达6天．（2）设从第一次喷洒起，经()610x x ≤≤天，浓度1888()24814628(6)1414a a a g x x x x x x x ⎛⎫=-+=-+=-+- ⎪----⎝⎭，因为[]144,8x -∈，而14a ≤≤，所以8()1466614a g x x x =-+-≥=-，当且仅当81414a x x -=-，即14x =-时，等号成立，令64-≥，解得258a ≥，。

成都高2026届高一数学十月阶段性测试（答案在最后）一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.下列集合符号运用不正确的是()A.2Z ∈B.}{}{1,2,31,2⊆ C.{}12⋂∅=∅，D.N R R⋃=【答案】B 【解析】【分析】根据集合知识,逐项分析,即可求得答案.【详解】对于A,由2Z ∈,故A 正确;对于B,因为}{}{1,21,2,3⊆,故B 错误;对于C,因为{}12⋂∅=∅，,故C 正确;对于D,因为N R R ⋃=,故D 正确.故选:B.【点睛】解题关键是掌握集合的基础知识,考查了分析能力,属于基础题.2.已知全集U =R ，集合{1,2,3,4,5},{2}A B x Rx ==∈≥∣，则图中阴影部分所表示的集合为（）A.{1}B.{0,1}C.{1,2}D.{0,1,2}【答案】A 【解析】【分析】根据图像判断出阴影部分表示()U A B ð，由此求得正确选项.【详解】根据图像可知，阴影部分表示()U A B ð，{}U |2B x x =<ð，所以()U A B ð{}1=.故选：A【点睛】本小题主要考查集合交集与补集的概念和运算，考查韦恩图，属于基础题.3.命题“1x ∀≤，2210x x -+≥”的否定是（）A.1x ∀>，2210x x -+<B.1x ∃>，2210x x -+<C.1x ∀≤，2210x x -+<D.1x ∃≤，2210x x -+<【答案】D 【解析】【分析】根据全称量词命题与存在量词命题的关系，准确改写，即可求解.【详解】根据全称命题与存在性命题的关系，可得命题“1x ∀≤，2210x x -+≥”的否定是“1x ∃≤，2210x x -+<”.故选：D.4.设集合{}2{2,},1,2A a B a ==--，若A B ⋂≠∅，则实数=a （）A.2-B.1- C.1-或2- D.1-或2±【答案】A 【解析】【分析】根据给定条件，利用交集的结果结合集合元素的性质求解作答.【详解】集合{}2{2,},1,2A a B a ==--，则2a ≠，且221a -≠-，解得2a ≠，且1a ≠±，由A B ⋂≠∅，得222a -=，或22a a -=，解222a -=，得2a =-或2a =（舍去）；解22a a -=，得1a =-（舍去）或2a =（舍去），所以2a =-.故选：A5.今有一台坏天平，两臂长不等，其余均精确，有人要用它称物体的质量，他将物体放在左右托盘各称一次，记两次称量结果分别为,a b ，设物体的真实质量为G ，则（）A.2a bG += B.2a bG +< C.2a bG +> D.G<【答案】C 【解析】【分析】根据物理知识可求真实重量为G ，利用基本不等式可得两者之间的大小关系.【详解】解：设天平的左右臂分别为1,2l l ，物体放在左右托盘称得的重量分别为,a b ,真实重量为G ,所以，由杠杆平衡原理知：12l G l a ⋅=⋅，21l G l b ⋅=⋅,所以，由上式得2G ab =，即G =，因为12l l ≠,a b ¹，所以，由均值不等式2a bG +>=，故选：C.6.已知a ，R b ∈且a b ¹，命题p ：a b >，命题q ：3322a b a b ab +>+，则命题p 是命题q 成立的（）条件A.充分不必要B.必要不充分C.充分必要D.既不充分也不必要【答案】A 【解析】【分析】对命题q 进行等价转化为a b >-，再根据充分不必要条件的判断即可得到答案.【详解】3322a b a b ab +>+，即()()()22a a ab ab b ba b -+>++，即()()()22a a ab ab b ba b -+>++，则命题3322:q a b a b ab +>+等价于2()()0a b a b -+>，因为a b ¹，则2()0a b ->，则0a b +>，即a b >-，而||a b >可以推出a b >-，反之，举例2,3a b =-=-，但||a b <，则反推无法推出，故||a b >是a b >-成立的充分不必要条件，故选：A.7.某学校举办运动会，比赛项目包括田径､游泳､球类，经统计高一年级有57人参加田径比赛，有11人参加游泳比赛，有62人参加球类比赛.参加球类比赛的同学中有14人参加田径比赛，有4人参加游泳比赛；同时参加田径比赛和游泳比赛的有8人；同时参加三项比赛的有2人.则高一年级参加比赛的同学有（）A.98人B.106人C.104人D.110【答案】B 【解析】【分析】根据韦恩图可求高一年级参加比赛的同学的人数.【详解】由上述韦恩图可得高一年级参加比赛的同学的人数为：11625748142106++---+=，故选：B.8.对R x ∀∈，[]x 表示不超过x 的最大整数，如[]3.143=，[]0.6180=，[]2.718283-=-，我们把[]y x =，x ∈R 叫做取整函数，也称之为高斯（Gaussian ）函数，也有数学爱好者形象的称其为“地板函数”，早在十八世纪，人类史上伟大的数学家，哥廷根学派的领袖约翰·卡尔·弗里德里希·高斯（Johann Carl FriedriCh Gaussian ）最先提及，因此而得名“高斯（Gaussian ）函数”．在现实生活中，这种“截尾取整”的高斯函数有着广泛的应用，如停车收费、EXCEL 电子表格，在数学分析中它出现在求导、极限、定积分、级数等等各种问题之中．则不等式[][]241250x x -+≤成立的充分不必要条件是（）A.1522x ≤≤ B.12x ≤≤C.13x ≤< D.13x ≤≤【答案】B 【解析】【分析】解不等式得到[]1522x ≤≤，确定13x ≤<，对比选项得到答案.【详解】[][]241250x x -+≤，则[]1522x ≤≤，故[]1x =或[]2x =，13x ≤<，对比选项知：13x ≤<成立的一个充分必要条件是12x ≤≤，其他选项不满足.故选：B.二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项是符合题目要求的．全部选对的得5分，部分选对的得2分，有选错的得0分．9.关于命题“2,0a a a ∃∈+≤N ”，下列判断正确的是（）A.该命题是全称量词命题B.该命题是存在量词命题C.该命题是真命题D.该命题是假命题【答案】BC【解析】【分析】根据存在量词命题、全称量词命题概念判断AB ，再由命题真假判断CD.【详解】2,0a a a ∃∈+≤N 是存在量词命题，∴A 选项错误B 选项正确；0a = 时，20a a +≤成立，∴命题为真命题，即C 正确D 错误.故选：BC10.若0a >，0b >，2a b +=，则下列不等式对一切满足条件的a ，b 恒成立的是（）A.1ab ≤B.≤C.222a b +≥D.112a b+≥【答案】ACD 【解析】【分析】分别根据基本不等式即可求出．【详解】2(12a b ab +≤=，当且仅当1a b ==时取等号，故A 成立；+≤，则2a b ++≤0≤，与已知矛盾，故B 不成立；2222()242()4222a b a b a b ab ++=+-≥-⨯=-=，当且仅当1a b ==时取等号，故C 成立；112a b a b ab ab ++==，由A 可得1122a b ab+=≥，当且仅当1a b ==时取等号，故D 成立.故选：ACD ．11.已知不等式20ax bx c ++>的解集为{}x m x n <<，其中0n m >>，则以下选项正确的有（）A.a<0B.0b >C.20cx bx a ++>的解集为11xx n m ⎧⎫<<⎨⎬⎩⎭D.20cx bx a ++>的解集为1x x n⎧<⎨⎩或1x m ⎫>⎬⎭【答案】ABC 【解析】【分析】根据二次不等式的解法，结合二次函数的性质，可得各参数的与零的大小关系，再结合韦达定理，可得选项中二次方程的解，可得答案.【详解】 不等式20ax bx c ++>的解集为{}x m x n <<，<0a ∴，故A 正确；0n m >> ，令()2f x ax bx c =++，02ba∴->，即0b >，故B 正确；由上所述，易知()00f <，0c <，由题意可得,m n 为一元二次方程20ax bx c ++=，则b m n a+=-，cmn a =，则11a n m c ⋅=，11m n b n m mn c ++==-，即11,n m为方程20cx bx a ++=的解，则可知不等式20cx bx a ++>的解集为11x x nm ⎧⎫<<⎨⎩⎭，故C 正确，D 错误.故选：ABC.12.定义集合运算{M N x x M -=∈且}x N ∉，称为集合M 与集合N 的差集；定义集合运算()()M N M N N M ∆=-- 称为集合M 与集合N 的对称差，有以下4个命题：则4个命题中是真命题的是（）A.M N N M ∆=∆B.()()M N P M N P ∆∆=∆∆C.()()()M N P M N M P ∆=∆ D.()()()M N P M N M P ∆=∆ 【答案】ABC 【解析】【分析】A 选项，通过题意得到M N N M ∆=∆；BCD 选项，通过韦恩图进行推理求解.【详解】A 选项，由题意得()M M N M N -= ð，()N N M M N -= ð，故()()M NM N M N M N ∆=痧，()()N M N M M N M N ∆= 痧，A 正确；B 选项，由题意，M N ∆表示的运算为集合M 与N 的并集中去掉M 与N 的交集部分，不妨设,,M N P 均有交集，如图所示，故M N ∆表示①②⑥⑦部分的并集，()M N P ∆∆表示①②⑥⑦与③④⑥⑦的并集去掉两者的交集，即()M N P ∆∆表示①②③④部分的并集，N P ∆表示②③⑤⑥部分的并集，()M N P ∆∆表示②③⑤⑥与①④⑤⑥的并集去掉两者的交集，即()M N P ∆∆表示①②③④部分的并集，故()()M N P M N P ∆∆=∆∆，B 正确；C 选项，通过推理()()(),M N P M N M P ∆∆ 均表示⑤⑥部分的并集，C 正确；D 选项，通过推理得到()M N P ∆ 表示①②③④⑤⑥部分的并集，M N ⋃表示①②④⑤⑥⑦部分的并集，M P ⋃表示①③④⑤⑥⑦部分的并集，()()M N M P ∆ 表示①②④⑤⑥⑦与①③④⑤⑥⑦的并集去掉两者的交集，即②③部分的并集，D 错误.故选：ABC三、填空题：本题共4小题，每小题5分，共20分．把答案填在答题卡上．13.已知集合{}{}22,1,3,3,21,1M a a P a a a =+-=--+，{}3M P ⋂=-，则=a _________.【答案】1-【解析】【分析】根据集合元素的互异性以及交集性质进行分类讨论即可得出1a =-符合题意.【详解】因为{}3M P ⋂=-，所以3P -∈，易知213a +≠-，当33a -=-时，0a =，此时{}0,1,3M =-，{}3,1,1P =--，不合题意舍去；当213a -=-时，1a =-，此时{}1,0,3M =-，{}4,3,2P =--，满足题意，故答案为：1-14.已知对一切23x ≤≤，36y ≤≤，不等式220mx xy y -+≥恒成立，则实数m 的最小值为______．【答案】0【解析】【分析】令[]1,3yt x=∈，则原题意等价于对一切[1,3]t ∈，2m t t ≥-恒成立，根据恒成立问题结合二次函数的性质分析运算.【详解】因为23x ≤≤，36y ≤≤，则111,32x ⎡⎤∈⎢⎥⎣⎦，所以，[]1,3yx∈，又不等式220mx xy y -+≥恒成立，且23x ≤≤，可得2y y m x x ⎛⎫≥- ⎪⎝⎭，令[]1,3yt x=∈，则原题意等价于对一切[1,3]t ∈，2m t t ≥-恒成立，因为2y t t =-，当1t =时，2max 110 y =-=，故实数m 的取值范围是0m ≥.15.已知23a b +=（0a >，0b >，N b ∈），则122a b+的最小值为______．【答案】2【解析】【分析】0a >，0b >，N b ∈，所以1b =或2b =，分类讨论.【详解】因为0a >，0b >，N b ∈，所以1b =或2b =，当1b =，1a =，故12152222a b +=+=，当2b =，12a =，故1211221a b +=+=，122a b+的最小值为2.故答案为：216.已知关于x 的不等式组()()220422770x x x a x a a +⎧<⎪-⎨⎪+++<∈⎩R 仅有一个整数解，则a 的取值范围为______．【答案】[)(]5,34,5-⋃【分析】求出第一个不等式的解，讨论a 的范围得出第二个不等式的解，根据不等式组织含有一个整数得出第二个不等式的端点的范围，从而求得a 的范围.【详解】由不等式204+<-x x，即()()240x x +->，解得<2x -或4x >，解方程()()()22277270+++=++=x a x a x x a ，解得172x =-或2x a =-，1.若72-=-a ，即72a =时，不等式()222770+++<x a x a 的解集为∅，不合题意；2.若72-<-a ，即72a >时，不等式()222770+++<x a x a 的解集为7,2⎛⎫-- ⎪⎝⎭a ，若不等式组只有1个整数解，则54-≤-<-a ，解得45a <≤；3.若72->-a ，即72a <时，不等式()222770+++<x a x a 的解集为7,2⎛⎫-- ⎪⎝⎭a ，若不等式组只有1个整数解，则35a -<-≤，解得53a -≤<；综上可得，实数a 的取值范围是[5,3)(4,5]- .故答案为：[)(]5,34,5-⋃四、解答题：本题共6小题，17题10分，18-22题每题12分，共70分．解答应写出文字说明、证明过程或演算步骤．17.已知集合A ＝{x |﹣2≤x ≤2}，B ＝{x |x ＞1}.（1）求集合R B A ⋂ð；（2）设集合M ＝{x |a ＜x ＜a +6}，且A ∪M ＝M ，求实数a 的取值范围.【答案】（1）{x |﹣2≤x ≤1}（2）{}42a a -<<-【解析】【分析】（1）进行补集和交集的运算即可；（2）根据A M M ⋃＝可得出A M ⊆，然后即可得出262a a <-⎧⎨+⎩＞，然后解出a 的范围即可．【小问1详解】{|}1B x x ＝＞，则{}R 1|x x B ≤＝ð，又}2{2|A x x ≤-≤＝，则R {|}21A x B x ⋂≤-≤＝ð；【小问2详解】∵A M M ⋃＝，∴A M ⊆，且}6{|M x a x a +＝＜＜，∴262a a <-⎧⎨+⎩＞，解得42a -＜＜-，∴实数a 的取值范围为:{}42a a -<<-18.已知命题p ：关于x 的方程222260x ax a a -+--=有实数根，命题:13q m a m -≤≤+．（1）若命题p ⌝是真命题，求实数a 的取值范围；（2）若p 是q 的必要不充分条件，求实数m 的取值范围．【答案】（1）(,2)(3,)-∞-⋃+∞（2）10m -≤≤【解析】【分析】（1）依题意命题p 是假命题，即可得到Δ0<，从而求出参数a 的取值范围；（2）记{}23|A a a -=≤≤，{}|13B a m a m =-≤≤+，依题意可得B A ，即可得到不等式组，解得即可.【小问1详解】解：因为命题p ⌝是真命题，所以命题p 是假命题．所以方程222260x ax a a -+--=无实根，所以222Δ(2)4(26)44240a a a a a =----=-++<．即260a a -->，即()()320a a -+>，解得3a >或2a <-，所以实数a 的取值范围是(,2)(3,)-∞-⋃+∞．【小问2详解】解：由（1）可知p ：23a -≤≤，记{}23|A a a -=≤≤，{}|13B a m a m =-≤≤+，因为p 是q 的必要不充分条件，所以BA ，所以1233m m -≥-⎧⎨+≤⎩（等号不同时取得），解得10m -≤≤，所以实数m 的取值范围是10m -≤≤．19.为宣传2023年杭州亚运会，某公益广告公司拟在一张矩形海报纸（记为矩形ABCD ，如图）上设计四个等高的宣传栏（栏面分别为两个等腰三角形和两个全等的直角三角形且2GH EF =），宣传栏（图中阴影部分）的面积之和为236000cm ．为了美观，要求海报上所有水平方向和竖直方向的留空宽度均为10cm ，设cm EF x =．（1）当100cm x =时，求海报纸的面积；（2）为节约成本，应如何选择海报纸的尺寸，可使用纸量最少（即矩形ABCD 的面积最小）？【答案】（1）249000;cm （2）选择长宽分别为350,140cm cm 的海报纸.【解析】【分析】（1）先表示出阴影部分的面积，代入100cm x =，可求出阴影部分的高，进而得到海报纸的面积；（2）表示出各自的关系式，转化为条件下的最值问题，最后运用基本不等式可得答案.【小问1详解】设阴影部分直角三角形的高为,ycm 所以阴影部分的面积：163360002S xy xy =⨯==，所以12000,xy =即：100,120x cm y cm ==，由图像知：20140,350350AD y cm AB x cm =+==+=，()214035049000.ABCD S cm ∴=⨯=【小问2详解】由（1）知：12000,0,0,xy x y =>>()()35020360501000321000ABCD S x y xy x y xy =++=+++≥+49000=，当且仅当65,x y =即100,120x cm y cm ==，即350,140AB cm AD cm ==等号成立.综上，选择长宽分别为350,140cm cm 的海报纸.20.已知一元二次不等式2320x x -+>的解集为A ，关于x 的不等式()2220mx m x -++<的解集为B （其中R m ∈）．（1）求集合B ；（2）在①R B A ⊆ð，②A B ⋂≠∅，③A B A ⋃=，这三个条件中任选一个，补充在下面问题的______中，若问题中的实数m 存在，求m 的取值范围：若不存在，说明理由．问题：是否存在实数m ，使得______？（注：如果选择多个条件分别解答，按第一个解答计分）．【答案】（1）答案见解析（2）答案见解析【解析】【分析】（1）由()2220mx m x -++<，得()()210mx x --<，从而根据m 的范围，分类讨论，解一元二次不等式即可；（2）由（1）{}12A x x x =或，若选择①R B A ⊆ð，则{}R 12A x x =≤≤|ð，从而列式求得m 的取值范围；若选择②，A B ⋂≠∅，根据m 的范围，分类讨论，利用交集运算得结论；若选择③，A B A ⋃=，则B A ⊆，由此可求出m 的取值范围．【小问1详解】解：由()2220mx m x -++<，即()()210mx x --<．①0m =时，1x >；②0m <时，1x >或2x m<；③02m <<时，21x m <<；④2m =时，不等式无解；⑤2m >时，21x m<<．综上所述：当0m =时，{}1B x x =>；当0m <时，2|1B x x x m ⎧⎫=><⎨⎬⎩⎭或；当02m <<时，2|1B x x m ⎧⎫=<<⎨⎬⎩⎭；当2m =时，B =∅；当m>2时，2|1B x x m ⎧⎫=<<⎨⎬⎩⎭．【小问2详解】由（1）{}12A x x x =或，若选择①R B A ⊆ð，则{}R 12A x x =≤≤|ð，由（1）可知：只有当02m <<，2|1B x x m ⎧⎫=<<⎨⎬⎩⎭，则有22m ≤，所以12m ≤<；另外，当2m =时，B =∅也成立，所以选择①，则实数m 的取值范围是12m ≤≤；若选择②，A B ⋂≠∅，由（1）可知：当0m =，0m <，2m >时，都能符合条件；当02m <<，2|1B x x m ⎧⎫=<<⎨⎬⎩⎭，则有22m>，所以01m <<所以选择②，则实数m 的取值范围是1m <或2m >；若选择③，A B A ⋃=，则B A ⊆，由（1）可知：只有当m>2时，2|1B x x A m ⎧⎫=<<⊆⎨⎬⎩⎭成立；另外，当2m =时，B =∅也成立所以选择③，则实数m 的取值范围是2m ≥．21.已知,,a b c 均为正实数，且2222a b c ++=.（1）求a b c ++的最大值；（2）求111a b b c c a+++++的最小值.【答案】（1（2）4【解析】【分析】（1）由2222()222a b c a b c ab bc ca ++=+++++，结合基本不等式即可求解；（2）令m a b =+，n b c =+，p c a =+，由111( ) m n p m n p ⎛⎫++++ ⎪⎝⎭展开，利用基本不等式得111()9m n pm n p ⎛⎫++++≥ ⎪⎝⎭，又由（1）知2()m n p a b c ++=++≤，代入求解即可.【小问1详解】∵2222()222a b c a b c ab bc ca ++=+++++，又222ab a b ≤+，222bc b c ≤+，222ca c a ≤+，∴()2222()36a b c a b c++≤++=，∴a b c ++≤，当且仅当3a b c ===时，等号成立，即a b c ++.【小问2详解】令m a b =+，n b c =+，p c a =+，则111( ) 3n p m p m n m n p m n p m m n n p p ⎛⎫++++=++++++ ⎪⎝⎭，∵2n m m n +≥，2≥p m p m +，2≥p n p n +，∴111()9m n p m n p ⎛⎫++++≥ ⎪⎝⎭，当且仅当m n p ==，即a b c ==时，等号成立，由（1）知2()m n p a b c ++=++≤，∴111111()m n p m n p m n p ⎛⎫⎫++++≤++ ⎪⎪⎝⎭⎭，∴1119m n p ⎫++≥⎪⎭，∴1114m n p ++≥，即111a b b c c a +++++≥，当且仅当3a b c ===时，等号成立，故111a b b c c a +++++的最小值为4.22.关于x 的方程2x a x +=（R a ∈）的解集为A （A ≠∅），关于x 的方程()22x a a x ++=（R a ∈）的解集为B （1）对于集合M ，N ，若x M ∀∈，x N ∈，则M N ⊆．求证：A B⊆（2）若A B =，求实数a 的取值范围．【答案】（1）证明见解析（2）3144a -≤≤【解析】【分析】（1）根据子集的定义，结合方程解的性质进行证明即可；（2）根据集合相等的定义，结合一元二次方程根的判别式分类讨论进行求解即可.【小问1详解】设0x A ∈，∴200x a x +=，将0x 带入方程()22x a a x ++=等式成立．∴0x 是方程()22x a a x ++=的解，∴0x B ∈，∴A B ⊆；【小问2详解】∵A ≠∅，∴20x x a -+=有实根，∴140a ∆=-≥，∴14a ≤，∵集合B 为方程()22x aa x ++=即42220x ax x a a +-++=的根的集合，由（1）的结论A B ⊆且集合A 为方程20x x a -+=根的集合，∴因式4222x ax x a a +-++分解后必定含有因式2x x a -+，由多项式的除法：()()4222221x ax x a a x x ax x a +-++=-++++，∵A B =，∴210x x a +++=无实根或其根为方程20x x a -+=的根，当210x x a +++=无实根时，()Δ1410a =-+<，解得34a >-，当210x x a +++=的根为方程20x x a -+=的根时，①当210x x a +++=有两不等实根时，由韦达定理，其根不可能与20x x a -+=的根相同；②当210x x a +++=有两相等实根时，即()1410a ∆=-+=即34a =-时，方程的根为12x =-，此根刚好是20x x a -+=的根，满足条件．综上：故a 的取值范围是3144a -≤≤.【点睛】关键点睛：本题的关键是根据集合相等的定义判断出210x x a +++=无实根或其根为方程20-+=的根. x x a。