第二章 连续时间系统的时域分析
- 格式:ppt
- 大小:1.55 MB
- 文档页数:84

连续时间系统的时域分析时域分析是对连续时间系统进行分析和研究的一种方法。
通过时域分析,可以了解系统的时间响应特性、稳定性以及系统的动态行为。
本文将从连续时间系统的时域分析方法、常用的时域参数以及时域分析在系统设计中的应用等方面进行详细介绍。
一、连续时间系统的时域分析方法连续时间系统的时域分析方法主要有两种:解析法和数值法。
1. 解析法:通过解析方法可以得到系统的解析表达式,从而分析系统的时间响应特性。
常用的解析方法包括微分方程法、拉普拉斯变换法和傅里叶变换法等。
- 微分方程法:对于线性时不变系统,可以通过设立系统输入和输出之间的微分方程,然后求解微分方程来得到系统的时间响应。
- 拉普拉斯变换法:通过对系统进行拉普拉斯变换,将微分方程转化为代数方程,从而得到系统的传递函数,进而分析系统的时间响应。
- 傅里叶变换法:通过对系统输入和输出进行傅里叶变换,将时域信号转化为频域信号,从而分析系统的频率响应。
2. 数值法:当系统的解析表达式难以获得或无法求解时,可以通过数值方法进行时域分析。
常用的数值方法包括欧拉法、中点法和四阶龙格-库塔法等。
- 欧拉法:通过差分近似,将微分方程转化为差分方程,然后通过计算差分方程的递推关系来得到系统的时间响应。
- 中点法:在欧拉法的基础上,在每个时间步长内,通过计算两个相邻时间点上的导数平均值来改进估计值,从而提高精度。
- 四阶龙格-库塔法:在中点法的基础上,通过对导数进行多次计算和加权平均,从而进一步提高精度。
二、常用的时域参数时域分析除了对系统的时间响应进行分析外,还可以提取一些常用的时域参数来描述系统的性能和特性。
1. 零点:系统的零点是指系统传递函数中使得输出为零的输入值。
2. 极点:系统的极点是指系统传递函数中使得输出无穷大的输入值。
3. 零极点图:零极点图是用来描述系统传递函数中的零点和极点分布情况的图形。
4. 频率响应:频率响应是指系统对不同频率的输入信号的响应。




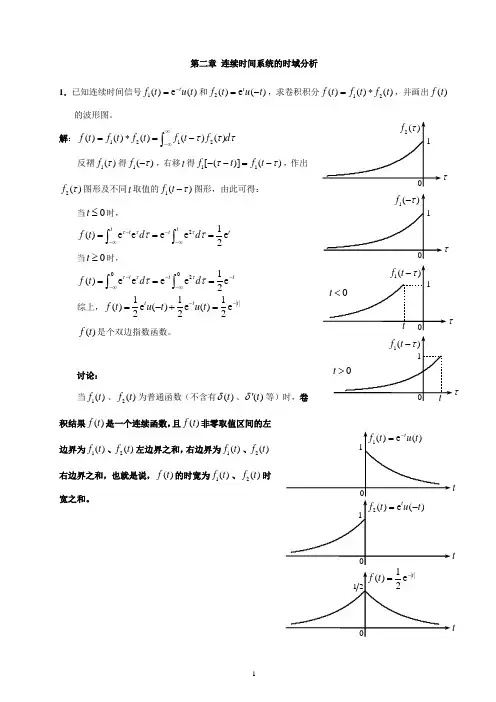
第二章 连续时间系统的时域分析1.已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-,求卷积积分12()()()f t f t f t =*,并画出()f t 的波形图。
解:1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-,右移t 得11[()]()f t f t ττ--=-,作出2()f τ图形及不同t 取值的1()f t τ-图形,由此可得:当0t ≤时,21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时,0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上,||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。
讨论:当1()f t 、2()f t 为普通函数(不含有()t δ、()t δ'等)时,卷积结果()f t 是一个连续函数,且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和,右边界为1()f t 、2()f t 右边界之和,也就是说,()f t 的时宽为1()f t 、2()f t 时宽之和。
τttt2.计算题图2(a )所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=,并画出)(t f 的图形。
解法一:图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b),由此可得: 当10t +≤,即1t ≤-时,()0f t = 当011t ≤+≤,即10t -≤≤时,120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤,即01t ≤≤时,1()21f t d ττ==⎰当011t ≤-≤,即12t ≤≤时,121()21(1)t f t d t ττ-==--⎰当11t -≥,即2t ≥时,()0f t =综上,220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。





第二章 连续时间系统的时域分析经典法:双零法卷积积分法:求零状态响应求解系统响应→定初始条件满足换路定则起始点有跳变:求跳变量零输入响应:用经典法求解零状态响应:卷积积分法求解()()()()⎩⎨⎧==-+-+0000L L c c i i u u例题•例题1:连续时间系统求解(经典法,双零法) •例题2:求冲激响应(n >m ) •例题3:求冲激响应(n <m ) •例题4:求系统的零状态响应 •例题5:卷积 •例题6:系统互联例2-1分析在求解系统的完全响应时,要用到有关的三个量是: :起始状态,它决定零输入响应;()()()()()()()()()强迫响应。
状态响应,自由响应,并指出零输入响应,零,求系统的全响应,已知 系统的微分方程为描述某t u t e r r t e t t e t r t t r t t r =='=+=++--,00,206d d 22d d 3d d LTI 22()-0)(k r ⎩⎨⎧状态变量描述法输出描述法—输入建立系统的数学模型:跳变量,它决定零状态响应; :初始条件,它决定完全响应;这三个量之间的关系是 分别利用 求零状态响应和完全响应,需先确定微分方程的特解。
解:方法一:利用 先来求完全响应,再求零输入响应,零状态响应等于完全响应减去零输入响应。
方法二:用方法一求零输入响应后,利用跳变量 来求零状态响应,零状态响应加上零输入响应等于完全响应。
本题也可以用卷积积分求系统的零状态响应。
方法一1. 完全响应 该完全响应是方程 (1)方程(1)的特征方程为 特征根为 方程(1)的齐次解为因为方程(1)在t >0时,可写为 (2)显然,方程(1)的特解可设为常数D ,把D 代入方程(2)求得 所以方程(1)的解为下面由冲激函数匹配法定初始条件 由冲激函数匹配法定初始条件 据方程(1)可设代入方程(1),得匹配方程两端的 ,及其各阶导数项,得 所以,所以系统的完全响应为()+0)(k zsr ()+0)(k r ()()()+-+=-000)()()(k zs k k r r r ()()++00)()(k k zs r r ,()()代入原方程有将t u t e =()()()()()t u t t r t t r t t r 622d d 3d d 22+=++δ()()++'0,0r r ()()++''0,0zs zs r r ()()()()()t u t t r t t r t t r 622d d 3d d 22+=++δ()()的解且满足00,20='=--r r 0232=++αα2121-=-=αα,()t t e A e A t r 221--+=()()()()t u t r t t r tt r 62d d 3d d 22=++3=D ()3221++=--tt e A e A t r ()()()t u b t a t t r ∆+=δ22d d ()()t u a t t r ∆=d d ()无跳变t r ()()()()()()t u t t r t u a t u b t a 6223+=+∆+∆+δδ2=a ()t δ()()22000=+=+'='-+a r r ()()200==-+r r ()()代入把20,20=='++r r ()3221++=--t t e A e A t r 1,021-==A A 得()0 32≥+-=-t e t r t ()t r zi 再求零输入响应2.求零输入响应 (3)(3)式的特征根为 方程(3)的齐次解即系统的零输入响应为所以,系统的零输入响应为 下面求零状态响应零状态响应=完全响应—零输入响应,即 因为特解为3,所以强迫响应是3,自由响应是方法二(5)以上分析可用下面的数学过程描述 代入(5)式 根据在t =0时刻,微分方程两端的 及其各阶导数应该平衡相等,得 于是t >0时,方程为 齐次解为 ,特解为3,于是有所以,系统的零状态响应为方法一求出系统的零输入响应为()是方程响应因为激励为零,零输入t r zi ()()()02d 3d d 22=++t r dt t r t t r ()()()()()()的解.,且满足 0000 2000='='='===--+--+r r r r r r zi zi zi zi 2121-=-=αα,()t t zi e B e B t r 221--+=()()式解得,代入,由)4(0020='=++zi zi r r 2,421-==B B ()0 242≥-=--t e e t r t t zi ()0 342≥++-=--t e e t r t t zs t t e e 24--+-()是方程零状态响应t r zs ()()()()()t u t t r t t r t t r 622d d 3d d 22+=++δ()()的解且满足000='=--zs zs r r ()项由于上式等号右边有t δ()应含有冲激函数,,故t r zs "()将发生跳变,即从而t r zs '()()-+'≠'00zs zs r r ()处是连续的.在而0=t t r zs ()()()()()t u a t r t t u b t a t r tzs zs∆=+∆+=+d d ,d d 22δ()()()()()()t u t t r t u a t u b t a 6223+=+∆+∆+δδ()t δ2=a ()()()()002000===+'='-+-+zs zs zs zs r r a r r ()()()()t u t r t t r t t r 62d d 3d d 22=++ 221t t e D e D --+()3221++=--t t zi e D e D t r ()()得由初始条件0,200=='++zs zs r r 1,421=-=D D ()0) ( 342≥++-=--t e e t r t t zs ()0 242≥-=--t e e t r t t zi完全响应=零状态响应+零输入响应,即例2-2冲激响应是系统对单位冲激信号激励时的零状态响应。