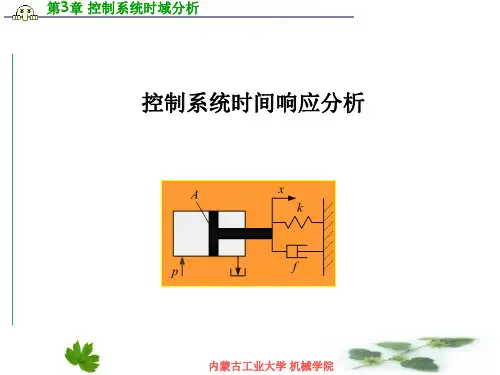
控制系统的时域分析
- 格式:doc
- 大小:844.00 KB
- 文档页数:13

实验5-控制系统时域分析实验目的:1. 掌握控制系统的时域分析方法;2. 熟悉控制系统的基本概念;3. 比较不同控制系统的性能指标,并对其优化。
实验原理:控制系统是由控制器、被控对象和传感器等组成的系统。
它的主要功能是将被控对象的输出值与预期输出值(设定值)进行比较,并根据比较结果对控制器的输出信号进行调整,以实现预期的控制系统动态响应。
系统的状态可以用输入输出关系来表示,通常用系统函数表示,它是输入信号与输出信号的转换函数。
根据系统函数的性质,系统的特性可以分析出来,比如稳态误差、响应时间和阻尼等。
控制系统的时域分析方法主要包括以下内容:1. 稳态误差分析稳态误差是指当控制系统到达稳定状态时,被控对象的输出值与设定值之间的差值。
它是一个反映控制系统偏离设定状态能力的指标。
稳态误差对于不同类型的系统有不同的计算方法,常见的系统类型包括比例控制系统、积分控制系统和派生控制系统。
比例控制系统的稳态误差是:$e_{ss}= \frac {k_p}{1+k_p}, (k_p \neq 0)$派生控制系统的稳态误差是0。
2. 基本响应特性分析一个控制系统的基本响应特性主要包括死区、超调量和稳定时间等。
死区是指当控制器输出的信号在一定范围内时,被控对象的输过不会发生变化。
死区对控制系统的响应时间和稳态误差有很大影响,通常需要根据系统的特点对死区进行调整。
超调量是指被控对象的输出值在达到设定值后,超出设定值的程度。
常见的超调量有百分比超调量和绝对超调量。
3. 阻尼及其影响阻尼是指系统的阻尼比,它是表征系统阻尼程度的一个参数。
阻尼对控制系统的稳定性和性能有很大影响。
当阻尼比为1时,系统的响应最快,但容易出现震荡现象。
阻尼比小于1时,系统的响应相对较慢,但是不会出现震荡现象。
当阻尼比大于1时,系统的响应速度较慢,但相对稳定。
实验步骤:本实验采用MATLAB软件对几种常见的控制系统进行时域分析,具体步骤如下:1. 打开MATLAB软件,新建文件进行编程。






控制系统时域分析控制系统是指由各种元件和装置组成的,用于控制、调节和稳定各种过程的系统。
在控制系统的设计和分析中,时域分析是一种常用的方法。
时域分析可以通过考察系统输出信号在时间上的变化来评估系统的性能和稳定性。
本文将介绍控制系统的时域分析方法及其在工程实践中的应用。
1. 时域分析的基本概念时域分析是指通过观察系统输入和输出信号在时间轴上的波形变化,来分析控制系统的性能和特性。
在时域分析中,常用的指标包括系统的响应时间、稳态误差、超调量、振荡频率等。
2. 系统的单位阶跃响应单位阶跃响应是指将系统输入信号设置为单位阶跃函数,观察系统输出信号的变化。
单位阶跃响应可以反映系统的动态特性,包括系统的稳态响应和暂态响应。
通过观察单位阶跃响应的波形,可以评估系统的超调量、上升时间、峰值时间等性能指标。
3. 系统的单位脉冲响应单位脉冲响应是指将系统输入信号设置为单位脉冲函数,观察系统输出信号的变化。
单位脉冲响应可以用来确定系统的传递函数和冲激响应。
通过观察单位脉冲响应的波形,可以计算系统的阶跃响应和频率响应等特性。
4. 系统的稳态误差分析稳态误差是指系统输出信号与期望输出信号之间的偏差。
稳态误差分析是用来评估系统在稳态下的性能。
根据系统的稳态误差特性,可以对系统进行进一步的补偿和优化。
通常,稳态误差可以通过单位阶跃响应和传递函数来计算。
5. 系统的波形分析波形分析是指通过观察系统输入和输出信号的波形,来分析系统的性能和特性。
波形分析可以帮助工程师判断系统是否存在超调、振荡和阻尼等问题,从而进行相应的调整和改进。
6. 控制系统的频域分析虽然时域分析是评估控制系统性能的常用方法,但有时候需要使用频域分析来更全面地了解系统的特性。
频域分析可以通过考察系统的频率响应函数来评估系统的稳定性和抗干扰性能。
常见的频域分析方法包括傅里叶变换、拉普拉斯变换和频率响应曲线等。
总结:时域分析是控制系统设计和分析中重要的工具之一。
通过观察系统输入和输出信号在时间上的变化,可以评估系统的性能和稳定性。



实验报告
实验名称:实验1:控制系统的时域分析
课程名称:自控控制原理
专业:电气工程及其自动化
班级:130037
学生姓名:施苏伟
班级学号:13003723
指导教师:杨杨
实验日期:2015 年10 月16日
一、实验目的
1.观察控制系统的时域响应;
2.记录单位阶跃响应曲线;
3.掌握时间响应分析的一般方法;
4.初步了解控制系统的调节过程。
二.实验步骤:
1.将‘实验一代码’这个文件夹拷贝到桌面上;
2.开机进入Matlab6.1 运行界面(其他版本亦可);
3.通过下面方法将当前路径设置为‘实验一代码’这个文件夹所在的路径
4.Matlab 指令窗>>后面输入指令:con_sys; 进入本次实验主界面。
5.分别双击上图中的三个按键,依次完成实验内容。
6.本次实验的相关Matlab 函数:
传递函数G=tf([num],[den])可输入一传递函数,其中num、den 分别表示分子、分母按降幂排列的系数。
三、仿真结果:
(一)观察一阶系统G=1/(T+s)的时域响应:
T=5s
T=8s
T=13s
结果分析:一阶系统 G=1/(T+s)的,通过观察曲线发现,随着时间常数T的增大,同种响应要达到相同响应的时间增大,说明T越大,响应越慢。
(二)二阶系统的时域性能分析
(1)
结果分析:自然频率和阻尼比的适当时,通过调节相应的时间,阶跃响应可以得到稳定值。
(2)数据一:自然频率=5.96rad/sec
阻尼比=0.701
数据二:自然频率=8.2964rad/sec
阻尼比=0.701
结果分析:要达到既定范围,自然频率增大阻尼比要随之增大
(3)
结果分析:在自然频率不变,随着阻尼比的增大,极点逐渐靠近虚轴,纵坐标逐渐变大,β逐渐减小。
(4)
结果分析:在阻尼比不变的情况下,自然频率增大,极点逐渐远离虚轴,纵坐标减小,β不变。
说明自然频率对系统阶跃响应的上升时间、峰值时间和调节时间都有影响,不影响超调量。
(三)观察比例-微分校正与测速反馈对二阶系统的性能改善
(1)
(2)
结果分析:改变二阶系统传递函数分母,使零极点分布发生变化,阶跃响应随之发生变化,零极点分布改变即自然频率与阻尼比发生改变,所以阶跃响应各种指数发生改变。
(3)
结果分析:使用比例微分控制,系统性能得到明显改善。
比例微分控制可以增大系统的阻尼比,减小阶跃响应的超调量,缩短调节时间。
(4)
结果分析:使用比例微分控制,系统性能得到明显改善。
比例微分控制可以增大系统的阻尼比,减小阶跃响应的超调量,缩短调节时间。
(5)
结果分析:K3、K4都会对系统的各项指数发生变化,同时会有多组K3、K4的值满足实验要求。
四、实验小节
本次实验虽然只是按照要求一步一步做,看似简单,但是在做的过程中却有颇多感触,让我对控制系统的时域响应有更加直观的认识。
使我对自然频率、阻尼比、调节时间对
二阶系统的影响有了更加深刻的了解,实验三更是让我大开眼界,比例微分控制的调节对阶跃响应的改善有极大的作用,对缩短调节时间作用也是极大。