内齿变位啮合齿轮计算
- 格式:xls
- 大小:259.00 KB
- 文档页数:7
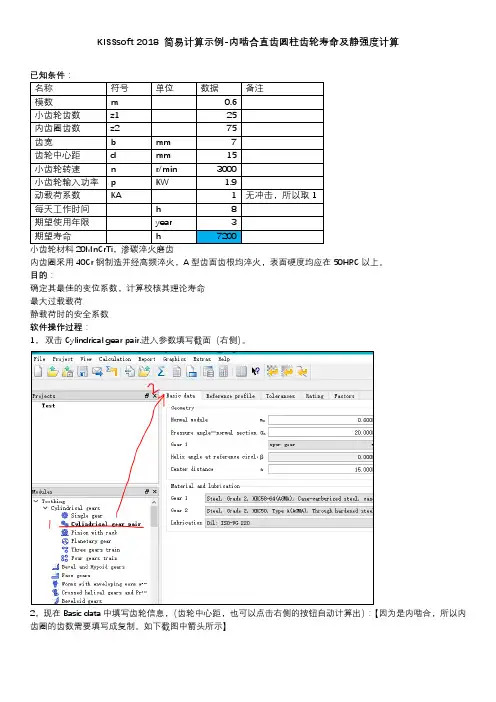
KISSsoft 2018 简易计算示例-内啮合直齿圆柱齿轮寿命及静强度计算
内齿圈采用40Cr钢制造并经高频淬火,A型齿面齿根均淬火,表面硬度均应在50HRC以上。
目的:
确定其最佳的变位系数,计算校核其理论寿命
最大过载载荷
静载荷时的安全系数
软件操作过程:
1,双击Cylindrical gear pair.进入参数填写截面(右侧)。
2,现在Basic data中填写齿轮信息,(齿轮中心距,也可以点击右侧的按钮自动计算出):【因为是内啮合,所以内齿圈的齿数需要填写成复制。
如下截图中箭头所示】
也可以进入Data base tool中,根据需要添加自己需要的材料用以计算:
3,点击下图按钮进入齿轮变位系数确认界面:
4,选择第一种方式计算变位系数。
点击OK。
得到推荐的变位系数。
5,填写Rating标签页中填写载荷和计算信息:
6,点击下图中的计算按钮即可计算齿轮寿命情况。
计算结果如下:(理论寿命满足使用要求)
Internal_gear_cal
culation-report1.pdf 计算最大载荷,按静载荷计算:
1,将计算方法改成Static calculation,点击计算按钮(前面第6部用到的按钮)
此时会出现如下提示,在计算静载荷时,软件会自动将需求寿命改成0小时,如下截图:
计算结果如下:
Internal_gear_cal culation-report-stati。

变位齿轮传动的受力分析和强度计算原理与标准齿轮的相同,其计算公式也与标准齿轮相同
齿轮啮合节点位置发生变化,Z H 有变化
2/
2cos tan H Z a a =2/2cos tan H t t Z a a =/a a =/t t a a =高高高高高高 高x Σ=x 1+x 2=0:
Z H 高高高高高高高高高高高高高
或/a a >/t t a a >/a a </t t
a a <高x Σ>0高高高高高高高高Z H 高高高εα高高高Z ε高高高
高Z H 高高高εα高高高Z ε高高高或齿面接触强度提高。
当xΣ<0(负传动)时,或齿面接触强度降低。
角变位传动即x Σ=x 1+x 2≠0 :
二、齿根弯曲强度齿根弯曲强度:
变位使齿形变化,齿根厚度和齿根圆角半径变化,引起计算系数Y Fa 和Y sa 的变化,影响齿根弯曲强度。
正变位齿轮的齿厚增大,Y Fa 减小,
齿根圆角半径减小,Y sa 增大。
正变位齿轮的齿根弯曲强度可有提高。
负变位使齿根弯曲强度降低。
变位使端面重合度系数εa 变化,Y ε也发生变化。

变位齿轮参数计算公式引言变位齿轮是一种常用的齿轮传动装置,可以实现不等速传动。
在实际设计和计算中,需要了解和确定变位齿轮的参数,以便满足传动需求。
本文将介绍一些常用的变位齿轮参数计算公式,帮助读者了解和计算变位齿轮的相关参数。
1. 转速比计算公式对于一个变位齿轮传动系统,转速比是一个重要的参数,表示两轴之间的转速比例关系。
通常以N1、N2分别表示第一齿轮的转速和第二齿轮的转速。
变位齿轮的转速比计算公式如下:转速比 = (N2 - N1) / N12. 锥齿轮的齿数计算公式对于一对变位齿轮中的锥齿轮,其齿数计算公式如下:Z = (Z1 * m1) / m2其中,Z为锥齿轮的齿数,Z1为直齿轮的齿数,m1为直齿轮的模数,m2为锥齿轮的模数。
3. 螺旋角计算公式螺旋角是变位齿轮的一个重要参数,表示齿轮齿线沿轴向的倾斜角度。
对于一对变位齿轮中的螺旋齿轮,其螺旋角的计算公式如下:β = atan(tan(α) - (m2 * (Z2 - Z1)) / (2 * π * a))其中,β为螺旋角,α为压力角,m2为齿数为Z2的螺旋齿轮的模数,Z1为另一齿轮的齿数,a为啮合齿轮的轴向分度圆半径。
4. 齿面距计算公式齿面距是变位齿轮的另一个重要参数,表示两个啮合齿轮齿面上同一点之间的距离。
对于一对变位齿轮中的两个螺旋齿轮,其齿面距的计算公式如下:h = m2 * b / cos(α)其中,h为齿面距,m2为螺旋齿轮的模数,b为螺旋齿轮的齿宽,α为压力角。
5. 压力角计算公式压力角是变位齿轮设计中的一个重要参数,表示齿形曲线的锋角与轴线的夹角。
通常使用以下计算公式得到压力角的值:cos(α) = (Z1 + Z2) / (2 * m2 * a)其中,α为压力角,Z1和Z2分别为两个啮合齿轮的齿数,m2为螺旋齿轮的模数,a为啮合齿轮的轴向分度圆半径。
结论本文介绍了几个重要的变位齿轮参数计算公式,包括转速比、锥齿轮的齿数、螺旋角、齿面距和压力角的计算公式。

整理内齿变位啮合齿轮计算内齿变位啮合是齿轮传动中常见的一种变位啮合形式。
在内齿变位啮合中,齿轮的齿数由大到小递减,但是模数保持不变。
内齿变位啮合可以实现不同转速的齿轮传动,并且具有较大的变速范围和传动正精度。
内齿变位啮合齿轮的计算主要包括以下几个方面:1.齿轮参数的计算首先需要计算内齿轮和外齿轮的齿数、模数和压力角。
根据齿轮传动的要求和设计参数,确定内齿轮的齿数范围,然后选择合适的齿数。
模数一般是根据传动功率和齿轮尺寸来确定的。
压力角一般可取20°。
2.齿轮弧齿轮的计算内齿变位啮合齿轮的弧齿轮计算是内齿轮的重点。
弧齿轮的计算需要根据内齿轮的齿数和变位系数来确定。
变位系数是内齿轮的一项关键参数,一般需要根据设计要求和齿轮尺寸来确定。
3.齿轮啮合力的计算内齿变位啮合齿轮的啮合力主要包括齿面接触力和齿根挤压力。
齿面接触力可以通过计算齿轮的齿面接触弧长来确定,齿根挤压力可以通过计算齿轮齿根强度来确定。
齿轮啮合力的计算是内齿变位啮合齿轮设计的重要内容,需要合理选择齿轮材料和设计参数。
4.齿轮传动效率的计算齿轮传动效率是内齿变位啮合齿轮设计中需要考虑的一个重要指标。
齿轮传动效率的计算需要知道齿轮功率损失和输入功率,通过计算齿轮啮合力和齿轮传动系统的转速来确定。
综上所述,内齿变位啮合齿轮的计算是一个相对复杂的过程,需要综合考虑齿轮的齿数、模数、压力角、变位系数、弧齿轮、啮合力和传动效率等参数。
只有合理、准确地进行计算,才能设计出满足要求的内齿变位啮合齿轮传动系统。


内啮合齿轮泵参数计算公式概述说明以及解释1. 引言1.1 概述内啮合齿轮泵是一种广泛应用于液压传动系统中的重要元件。
它通过两个啮合的齿轮在壳体内部的运动,实现了液体的吸入和排出过程。
内啮合齿轮泵具有结构简单、工作可靠、体积小等优点,在各个领域都有着重要的应用。
1.2 文章结构本文将从以下几个方面对内啮合齿轮泵参数计算公式进行概述、说明和解释。
首先,我们会介绍内啮合齿轮泵的基本情况和参数计算的重要性。
接着,我们会详细解释推导内啮合齿轮泵参数计算公式的原理,并解释主要参数及其意义。
最后,我们会通过一个实例分析来展示如何使用这些公式进行参数计算,并得出相应的结论。
最后,我们会对本文进行总结,并展望未来研究方向。
1.3 目的本文旨在深入探究内啮合齿轮泵参数计算公式,并阐明其在实际工程中的应用价值。
通过对相关公式和原理进行详细介绍和解释,读者可以更加深入了解内啮合齿轮泵的参数计算方法,为实际应用提供参考和指导。
希望通过本文的阐述,能够增进对内啮合齿轮泵的理解,并为今后的研究和工程实践提供基础和启发。
2. 内啮合齿轮泵参数计算公式概述说明2.1 内啮合齿轮泵简介内啮合齿轮泵是一种常见的工业泵,它由内外啮合的齿轮组成,并通过齿轮的旋转来产生流体压力。
内啮合齿轮泵通常用于输送液体或润滑油,可以广泛应用于各个领域,如机械工程、石油工业和化工等。
2.2 参数计算的重要性在设计和使用内啮合齿轮泵时,准确地计算其参数至关重要。
这些参数包括流量、转速、功率、压力等。
通过正确计算这些参数,我们可以评估泵的性能和效率,并确定其适用范围。
参数计算也有助于我们理解内啮合齿轮泵的运行原理,并进行优化设计。
2.3 参数计算的应用领域内啮合齿轮泵参数计算广泛应用于以下领域:a) 设计与制造:在设计过程中,我们需要根据所需流量和压力来确定合适的泵型号和尺寸。
通过参数计算,可以选择最佳组件材料、确定齿轮的尺寸和几何形状,从而满足特定的工作要求。

内啮合齿轮副变位系数
内啮合齿轮副的变位系数选择需要考虑**防止齿顶过薄、确保合适的重合度以及避免干涉**等限制条件。
以下是关于内啮合齿轮副变位系数的一些详细信息:
1. **正变位的应用**:内啮合齿轮通常采用正变位(x2>0),这有助于避免渐开线干涉和径向干涉。
正传动(x2-x1>0)有利于避免过渡曲线干涉、重叠干涉,并可提高齿面接触强度。
2. **变位系数的选择**:选择内啮合齿轮的变位系数时,需要保证不产生任何形式的干涉,并且齿顶不宜过薄,重合度不应过小。
对于高变位齿轮,一般可以选择x1=x2在0.5到0.65之间。
而对于角变位齿轮,选择变位系数的方法较为复杂,需要参考相关资料。
3. **最小啮合角与变位系数**:在某些情况下,如少齿差内啮合齿轮副,可以通过使用牛顿迭代法和不同齿顶圆公式来获得最小啮合角的变位系数和啮合角。
研究表明,在满足重合度和齿廓干涉限制条
件下取得最小啮合角时,无论是采用滚齿还是插齿加工,顶隙混合制时少齿差内啮合齿轮副的啮合角和变位系数均较小。
4. **中心距与变位系数关系**:零齿差内啮合齿轮副中内外齿轮经变位后所能达到的最大中心距与各变位系数间存在一定的关系。
通过分析这种关系,可以导出啮合方程式,并确定啮合起讫点及其坐标计算式。
这些分析对于理解齿轮副的啮合过程和强度校核具有重要意义。
总的来说,在实际设计过程中,工程师还需要考虑实际工况和机构的安装空间,有时适当增加或减少变位系数来凑齿轮传动中心距,以满足特定的设计要求和功能需求。
因此,变位系数的选择是一个综合考虑多种因素的过程,需要依据具体的应用情况来决定。
一.带安全阀齿轮泵齿轮零件图所需参数表法面模数nm 4齿数z 10压力角α20°全齿高h 9.1199螺旋角β9.63°螺旋方向右变位系数x 0.40394精度等级8-7-7JL齿圈径向跳动Fr 0.050公法线长度变动公差Fw 0.040基节极限偏差±fpb ±0.016齿形公差ff0.014齿向公差Fb 0.011齿厚上偏差Ess -0.186下偏差Esi -0.288二.齿轮测绘和变位齿轮参数测量和计算一.任务内容:根据齿轮测绘的数据,计算出齿轮的各参数,为齿轮零件图提供正确数据。
二.准备知识1.变位齿轮的定义:通过改变标准刀具对齿轮毛坯的径向位置或改变标准刀具的齿槽宽度切制出的齿形为非标准渐开线齿形的齿轮。
2.齿轮类型判别:两齿轮为大小相同的一对斜齿轮,齿数为10。
因此,齿轮是变位齿轮。
标准的渐开线齿轮的最小齿数应是17个齿。
本齿轮泵中的齿轮齿数少于17个齿,就一定是变位齿轮。
变位齿轮使齿轮传动结构紧凑,齿轮的强度增加。
3.变位齿轮的类型变位齿轮有两大类:高度变位传动和角度变位传动,如下表所示。
传动类型高度变位传动又称零传动角度变位传动正传动负传动齿数条件z1+z2≥2Zmin z1+z2<2zmin z1+z2>2zmin 变位系数要求x1+x2=0,x1=-x2≠0x1+x2>0 x1+x2<0 传动特点a'=a, α'=α, y=0 a'>a, α'>α, y>0 a'<a, α'<α,y<0主要优点小齿轮取正变位,允许z1<zmin ,减小传动尺寸。
提高了小齿轮齿根强度,减小了小齿轮齿面磨损,可成对替换标准齿轮。
传动机构更加紧凑,提高了抗弯强度和接触强度,提高了耐磨性能,可满足a'>a 的中心距要求。
重合度略有提高,满足a'<a 的中心距要求。

变位内啮合直齿圆柱齿轮传动的计算公式1. 引言1.1 概述变位内啮合直齿圆柱齿轮传动是一种常见的机械传动方式,广泛应用于各种机械装置中。
在设计和分析变位内啮合直齿圆柱齿轮传动时,需要准确计算相关参数和力学特性,以确保传动系统的可靠性和高效性。
本文旨在介绍变位内啮合直齿圆柱齿轮传动的计算公式,帮助读者理解和应用这些公式。
1.2 文章结构本文主要分为四个部分:引言、变位内啮合直齿圆柱齿轮传动的计算公式、计算公式应用实例以及结论与展望。
下面将对每个部分进行详细说明。
1.3 目的本文的目的是介绍变位内啮合直齿圆柱齿轮传动的计算公式,并通过实际应用案例来说明其具体使用方法。
通过阅读本文,读者可以了解到如何根据给定的齿轮参数来计算接触比力和压力角,并学会分析结果和验证计算公式的准确性。
此外,本文还将展望后续研究方向和拓展,包括其他齿轮传动类型的计算公式研究。
通过本文的阅读,读者可以深入了解变位内啮合直齿圆柱齿轮传动,并在实际应用中灵活运用相关的计算公式。
2. 变位内啮合直齿圆柱齿轮传动的计算公式2.1 齿轮参数定义在变位内啮合直齿圆柱齿轮传动中,我们首先需要定义一些关键的齿轮参数。
这些参数包括:- 齿数:分别表示驱动轮和从动轮上的齿数,分别记为Z1和Z2。
- 模数:表示齿轮的常规参数,记为m。
- 压力角:表示啮合点处切线与轴线间的夹角,记为α。
- 分度圆直径:分别表示驱动轴和从动轴上的分度圆直径,分别记为D1和D2。
2.2 接触比力分析接触比力是变位内啮合直齿圆柱齿轮传动中一个重要的参数。
它可以用来评估传动过程中发生的载荷情况。
接触比力的计算公式如下所示:Ft = (P*D1*cosα)/Z1其中,Ft表示接触比力,P表示传递功率。
2.3 压力角计算方法压力角是变位内啮合直齿圆柱齿轮传动中另一个重要参数。
它影响着齿轮传动的性能和效率。
压力角的计算方法如下所示:cosα= cos(atan(tanα) - (1/m)*((Z2*sin(atan(tan α)))/sqrt(Z1^2-(Z2*cos(atan(tanα)))^2)))其中,cosα表示压力角,tanα表示压力角切线,Z1表示驱动轮的齿数,Z2表示从动轮的齿数。
变位齿轮齿顶圆齿根圆直径计算公式变位齿轮是一种常见的传动装置,用于传递动力和扭矩。
在设计和制造变位齿轮时,计算齿顶圆直径和齿根圆直径是非常重要的。
本文将介绍如何计算变位齿轮的齿顶圆直径和齿根圆直径的公式和方法。
变位齿轮的齿顶圆直径和齿根圆直径是通过模数来计算的。
模数是变位齿轮齿数与齿轮直径的比值。
齿顶圆直径和齿根圆直径的计算公式如下:齿顶圆直径 = (齿数+ 2) × 模数齿根圆直径 = (齿数+ 2) × 模数 - 2 × 齿高其中,齿数是指变位齿轮的齿数,齿高是变位齿轮齿槽的深度。
通过这两个公式,可以准确地计算出变位齿轮的齿顶圆直径和齿根圆直径。
在实际应用中,计算齿顶圆直径和齿根圆直径前,需要先确定变位齿轮的模数、齿数和齿高。
模数的选择需要考虑到变位齿轮的传动功率、转速和齿轮材料等因素。
齿数的确定通常根据设计要求和装配空间来确定。
齿高的选择需要满足变位齿轮的强度和传动效率要求。
在计算齿顶圆直径和齿根圆直径时,需要注意以下几点。
首先,齿数和齿高的单位必须一致,通常为毫米。
其次,计算结果应保留足够的有效数字,以确保计算的准确性。
最后,齿高的计算需要根据变位齿轮的齿型来确定,常见的齿型有直齿、渐开线齿和圆弧齿等。
通过计算齿顶圆直径和齿根圆直径,可以确定变位齿轮的几何尺寸。
这些尺寸对于变位齿轮的制造、装配和使用非常重要。
在制造过程中,需要根据计算结果来确定齿轮的加工工艺和机床设备。
在装配和使用过程中,需要根据齿顶圆直径和齿根圆直径来确定齿轮的配合间隙和传动效率。
计算变位齿轮的齿顶圆直径和齿根圆直径是非常重要的工作。
通过正确使用相应的公式和方法,可以准确地计算出变位齿轮的几何尺寸。
这对于变位齿轮的设计、制造和使用都具有重要意义。
希望本文能对读者理解和应用变位齿轮的计算公式有所帮助。
内啮合角变位圆柱齿轮计算内啮合角变位圆柱齿轮是一种常见的传动装置,其工作原理是通过两个啮合的齿轮,使能量传递到另一个轴上,实现力的传递和速度的变换。
在计算内啮合角变位圆柱齿轮的过程中,需要考虑齿轮的尺寸、齿数、啮合角等参数。
下面将详细介绍内啮合角变位圆柱齿轮的计算方法。
首先,根据传动比和输入轴的转速,可以确定输出轴的转速。
传动比定义为输出轴的转速与输入轴的转速之比。
传动比=输出轴转速/输入轴转速其次,根据输入轴的转速和输出轴的转速,可以确定两个齿轮之间的齿数比。
齿数比定义为输出轴齿轮的齿数与输入轴齿轮的齿数之比。
齿数比=输出轴齿数/输入轴齿数知道齿数比之后,可以通过齿数比和齿轮模数来计算齿轮的齿数。
齿形尺寸的计算公式如下:齿数=齿数比*输入轴齿数然后,根据齿数和齿轮模数,可以计算齿轮的分度圆直径。
齿轮的分度圆直径定义为齿轮齿数除以齿轮模数。
分度圆直径=齿数/齿轮模数接下来,可以根据齿轮的分度圆直径和齿轮模数计算齿轮的外径和内径。
齿轮的外径定义为分度圆直径加上两倍的齿距。
齿距是指齿轮齿数除以齿轮模数。
外径=分度圆直径+2*齿距齿轮的内径是指分度圆的直径。
因此,齿轮的内径等于齿轮的分度圆直径。
内径=分度圆直径最后,可以通过输入轴和输出轴的转速计算出两个齿轮的啮合角。
啮合角是指两个齿轮轴上对应点的角度差。
啮合角=输入轴转速*360/输出轴转速通过以上计算方法,可以得到内啮合角变位圆柱齿轮的尺寸、齿数、啮合角等参数。
在实际应用中,还需要考虑齿轮的材料强度、齿面硬度等因素,以确保齿轮传动的可靠性和稳定性。
内齿变位啮合齿轮计算
首先,我们需要确定内齿圈和外齿圈的齿数。
假设内齿圈的齿数为
Z1,外齿圈的齿数为Z2、根据内齿变位啮合齿轮的特点,齿数之差
Δz=Z2–Z1必须是一个质数。
接下来,我们需要计算变位量。
变位量ε可以通过以下公式进行计算:
ε=πd1/Z1–πd2/Z2
其中,d1和d2分别是内齿圈和外齿圈的基圆直径。
基圆直径可以通过以下公式进行计算:
d=mZ
其中,m是齿轮模数,Z是齿数。
在计算变位量ε之后,我们还需要根据齿向变位量ε的大小,确定内齿圈和外齿圈的位置关系。
当ε>0时,内齿圈在外齿圈的左侧;当
ε<0时,内齿圈在外齿圈的右侧。
除了齿数和齿向变位量的计算外,还需要注意以下几点:
1.内齿圈和外齿圈的齿形必须满足啮合条件,即齿形要保持良好的啮合。
2.内齿圈和外齿圈的啮合角不能太大,一般应在20度以内。
3.内齿圈和外齿圈的啮合传动比可以根据齿数和齿向变位量的关系进行计算。
综上所述,内齿变位啮合齿轮的计算涉及到齿数、齿向变位量、基圆直径等参数的计算。
通过计算这些参数,我们可以确定内齿圈和外齿圈的位置关系,保证其正常的啮合。
同时,我们还需要根据实际应用需求,选择合适的齿轮材料和精度等级,保证齿轮的使用寿命和传动效率。
内啮合齿轮齿顶圆和齿根圆的计算公式好的,以下是为您生成的文章:咱们在机械传动领域里头,内啮合齿轮那可是个相当重要的角色。
今儿个,咱就好好唠唠内啮合齿轮齿顶圆和齿根圆的计算公式。
先来说说这齿顶圆。
想象一下,你正在一个大工厂里,机器轰鸣,各种零件在生产线上欢快地跑着。
其中就有内啮合齿轮在发挥着重要作用。
就像我之前在一家工厂实习的时候,看到师傅们在研究一个大型设备的传动系统,其中就涉及到内啮合齿轮的设计。
那时候,我就在旁边瞪大眼睛看着,心里充满了好奇。
对于内啮合齿轮的齿顶圆,它的计算公式是:$Da = d - 2ha - 2c$ 。
这里面,$Da$ 表示齿顶圆直径,$d$ 是齿轮的分度圆直径,$ha$ 是齿顶高,$c$ 是顶隙。
齿顶高 $ha$ 呢,通常等于 $ha = m(ha^* + x)$ ,其中 $m$ 是模数,$ha^*$ 是齿顶高系数,$x$ 是变位系数。
这就好比搭积木,每个参数都是一块特定形状的积木,按照一定规则组合在一起,就能搭出我们想要的“齿顶圆”这个大城堡。
再讲讲齿根圆。
齿根圆直径 $Df = d + 2hf - 2c$ 。
这里的 $hf$ 是齿根高,一般 $hf = m(ha^* + c^*)$ ,$c^*$ 是顶隙系数。
举个例子来说,假如有一个内啮合齿轮,模数 $m = 5$ ,分度圆直径 $d = 100$ ,齿顶高系数 $ha^* = 1$ ,顶隙系数 $c^* = 0.25$ ,变位系数 $x = 0.5$ 。
那先算齿顶高 $ha = 5×(1 + 0.5) = 7.5$ ,顶隙 $c =5×0.25 = 1.25$ ,齿根高 $hf = 5×(1 + 0.25) = 6.25$ 。
接着算齿顶圆直径$Da = 100 - 2×7.5 - 2×1.25 = 85$ ,齿根圆直径 $Df = 100 + 2×6.25 -2×1.25 = 110$ 。