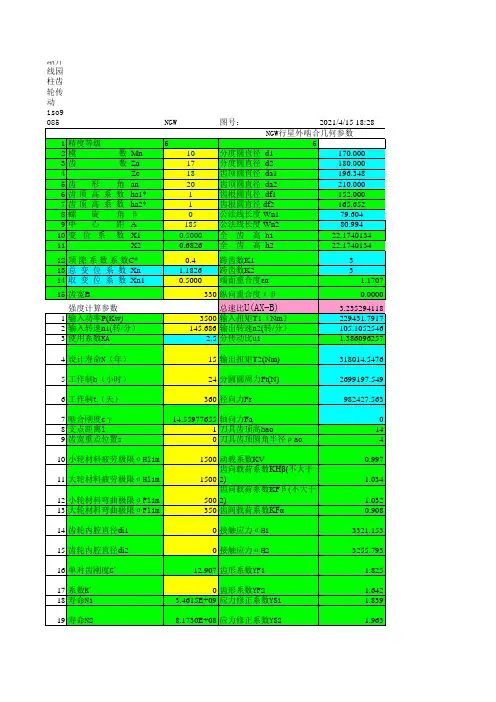
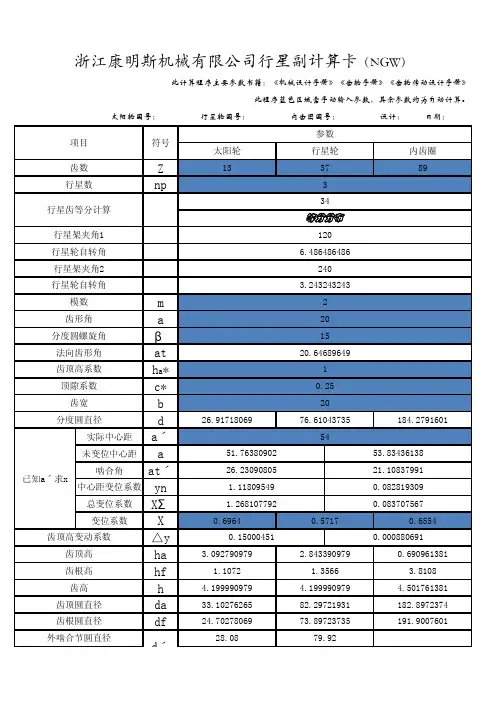
行星齿轮计算

在《机械原理》上，行星齿轮求解是通过列一系列方程式求解，其求解过程繁琐容易出错，其实用不着如此，只要理解了传动比eab i 的含义，就可以很快地直接写出行星齿轮的传动比，其关键是掌握几个根据e ab i 的含义推导出来公式，随便多复杂的行星齿轮传动机构，根据这几个公式都能从头写到尾直接把其传动比写出来，而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。

一式求解行星齿轮传动比有三个基本的公式1=+c ba a bc i i ――――――――――――――――――――――――1 a cx a bxa bc i i i = ―――――――――――――――――――――――――2a cb a bc i i 1= ――――――――――――――――――――――――――3熟练掌握了这三个公式后，不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。

关键是要善于选择中间的一些部件作为参照，使其最后形成都是定轴传动，所以这些参照基本都是一些行星架等例如象论坛中“大模王”兄弟所举的例子：在此例中，要求出e ab i ＝，如果行星架固定不动的话，这道题目就简单多了，就是一定轴传动。

所以我们要想办法把e ab i 变成一定轴传动，所以可以根据公式a cx a bx a bci i i =将x 加进去， 所以可以得出：e bx e ax eab i i i =要想变成定轴传动，就要把x 放到上面去，所以这里就要运用第一个公式1=+c ba abc i i 了，所以)1()1(xbe x ae ebx e ax eab i i i i i --==所以现在eab i 就变成了两个定轴传动之间的关系式了。

定轴传动的传动比就好办了，直接写出来就可以了。

即)1()1())1(1())1(1()1()1(01c e bd ae c e b d c e a c x be x ae e bx e ax e ab Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i i ⨯-+=⨯--⨯--=--== 再例如下面的传动机构：已知其各轮的齿数为z 1=100，z 2=101，z 2’ =100 ，z 3=99。

行星齿轮设计计算行星齿轮是一种常见的传动装置，常用于机械设备中的传动系统。

它由一个外部齿轮（太阳轮）和若干个内部齿轮（行星轮）组成，通过它们之间的齿轮传动来实现力的传递和速度的转换。

行星齿轮的设计是基于行星运动的原理。

在行星齿轮中，太阳轮位于中心位置，而行星轮则围绕太阳轮旋转。

行星轮的内部和外部都有齿轮，内部齿轮与太阳轮啮合，外部齿轮则与内部齿轮相连。

当太阳轮旋转时，行星轮也会随之旋转，从而实现力的传递和速度的转换。

行星齿轮的设计需要考虑多个因素。

首先，需要确定传动比。

传动比是指输出轴转速与输入轴转速的比值，它决定了行星齿轮的速度转换效果。

传动比可以通过改变行星轮和太阳轮的齿数来实现。

一般来说，行星轮的齿数越多，传动比越大；太阳轮的齿数越多，传动比越小。

还需要考虑行星轮的支撑方式。

行星轮通常由一个或多个支撑臂支撑，以确保其在旋转过程中保持稳定。

支撑臂的数量和位置对行星齿轮的传动效果有影响。

通常情况下，行星轮的支撑臂数量应为太阳轮齿数的一半，并且尽量均匀分布。

还需要考虑行星轮的啮合方式。

行星轮和太阳轮之间的齿轮传动需要确保牙齿之间的啮合紧密而不产生间隙。

为了实现这一点，行星轮的齿数和太阳轮的齿数需要满足一定的条件。

一般来说，行星轮的齿数应为太阳轮齿数的整数倍，以确保齿轮之间的啮合。

行星齿轮的设计还需要考虑传动效率和承载能力。

传动效率是指输入功率与输出功率之间的比值，而承载能力则是指行星齿轮能够承受的最大力矩。

为了提高传动效率和承载能力，行星齿轮的齿轮材料应选择高强度和高硬度的材料，并且需要进行适当的润滑和冷却。

行星齿轮是一种常见的传动装置，通过太阳轮和行星轮之间的齿轮传动来实现力的传递和速度的转换。

在设计行星齿轮时，需要考虑传动比、支撑方式、啮合方式、传动效率和承载能力等因素，以确保其稳定可靠的传动效果。

通过合理的设计和选择材料，行星齿轮能够广泛应用于各种机械设备中，提高传动效率和工作性能。

行星齿轮简易计算公式行星齿轮是一种常用的传动装置，它由太阳轮、行星轮、行星架和内齿圈组成。

行星齿轮传动具有传动比大、体积小、传动平稳等优点，因此在机械传动中得到广泛应用。

在实际工程中，需要对行星齿轮进行计算，以确定其传动性能和结构尺寸。

本文将介绍行星齿轮的简易计算公式，并对其进行详细解析。

行星齿轮传动的传动比计算公式如下：$$i = (1 + \frac{Zs}{Zp}) \times (1 \frac{Zs}{Zr})$$。

其中，i为传动比，Zs为太阳轮的齿数，Zp为行星轮的齿数，Zr为内齿圈的齿数。

行星齿轮传动的传动效率计算公式如下：$$\eta = \frac{\sin(\beta)}{\sin(\alpha)}$$。

其中，β为行星轮的压力角，α为太阳轮和内齿圈的压力角。

行星齿轮传动的载荷计算公式如下：$$T = \frac{9550 \times P}{n}$$。

其中，T为行星齿轮的扭矩，P为传动功率，n为转速。

行星齿轮传动的模数计算公式如下：$$m = \frac{1.25 \times P}{\sqrt{T}}$$。

其中，m为模数，P为传动功率，T为行星齿轮的扭矩。

以上公式是行星齿轮传动中常用的计算公式，通过这些公式可以快速计算出行星齿轮传动的传动比、传动效率、载荷和模数等参数，为行星齿轮的设计和选型提供了便利。

在实际工程中，行星齿轮传动的计算还需要考虑许多其他因素，如齿轮的材料、齿轮的强度、齿轮的精度等。

这些因素对行星齿轮传动的性能和寿命都有重要影响，需要进行综合考虑和分析。

在行星齿轮传动的设计过程中，还需要进行齿轮的强度计算。

齿轮的强度计算是为了确定齿轮的尺寸和材料，以保证齿轮在工作过程中不会发生破坏。

齿轮的强度计算包括齿面弯曲强度、齿根弯曲强度和齿面接触疲劳强度等方面，需要进行详细的计算和分析。

另外，行星齿轮传动的设计还需要进行齿轮的动力学分析。

齿轮的动力学分析是为了确定齿轮在工作过程中的振动和噪声情况，以保证齿轮的稳定性和平稳性。

大行星齿轮传动比计算公式大行星齿轮传动是一种常用的传动方式，广泛应用于工程机械、汽车等领域。

在设计和分析大行星齿轮传动系统时，计算传动比是非常重要的一步。

本文将介绍大行星齿轮传动比的计算公式及其应用。

一、大行星齿轮传动的基本结构大行星齿轮传动由太阳齿轮、行星齿轮、内齿圈和行星架等部分组成。

其中，太阳齿轮固定不动，内齿圈与外部传动轴相连，行星齿轮通过行星架与太阳齿轮和内齿圈相连。

二、大行星齿轮传动比的定义大行星齿轮传动比是指输入轴（太阳齿轮）的转速与输出轴（内齿圈）的转速之比。

传动比的大小决定了输出轴的转速和扭矩。

三、大行星齿轮传动比的计算公式大行星齿轮传动比可以根据行星齿轮传动的结构特点进行计算。

以下是常用的两种计算公式：1. 太阳齿轮传动比公式传动比=（内齿圈齿数+太阳齿数）/太阳齿数2. 行星齿轮传动比公式传动比=内齿圈齿数/行星齿数以上两种计算公式适用于不同的大行星齿轮传动结构，根据实际情况选择合适的公式进行计算。

四、大行星齿轮传动比的应用大行星齿轮传动比的计算在工程设计和分析中具有重要的意义。

以下是一些常见的应用场景：1. 机械设计中，通过计算传动比可以确定输出轴的转速和扭矩，从而满足设计要求。

2. 汽车传动系统中，大行星齿轮传动被广泛应用于变速器中。

通过计算传动比，可以实现不同档位之间的转速匹配，提高汽车的行驶性能和燃油经济性。

3. 工程机械中，大行星齿轮传动常用于液压马达的传动系统。

通过计算传动比，可以确定液压马达的输出速度和扭矩，从而实现机械装置的正常工作。

五、总结大行星齿轮传动比的计算是大行星齿轮传动系统设计和分析中的重要环节。

本文介绍了大行星齿轮传动比的计算公式及其应用，希望对读者理解和应用大行星齿轮传动有所帮助。

六、参考文献1. 《机械设计基础》（杨文彬、陈涛著，中国水利水电出版社）2. 《汽车传动系统设计与分析》（郑敏著，机械工业出版社）。

行星齿轮传动比计算在《机械原理》上，行星齿轮求解是通过列一系列方程式求解，其求解过程繁琐容易出错，其实用不着如此，只要理解了传动比eab i 的含义，就可以很快地直接写出行星齿轮的传动比，其关键是掌握几个根据e ab i 的含义推导出来公式，随便多复杂的行星齿轮传动机构，根据这几个公式都能从头写到尾直接把其传动比写出来，而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。

一式求解行星齿轮传动比有三个基本的公式1=+c ba a bc i i ――――――――――――――――――――――――1a cxa bxa bcii i =―――――――――――――――――――――――――2 acba bci i 1= ――――――――――――――――――――――――――3熟练掌握了这三个公式后，不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。

关键是要善于选择中间的一些部件作为参照，使其最后形成都是定轴传动，所以这些参照基本都是一些行星架等例如象论坛中“大模王”兄弟所举的例子：在此例中，要求出eab i ＝，如果行星架固定不动的话，这道题目就简单多了，就是一定轴传动。

所以我们要想办法把e ab i 变成一定轴传动，所以可以根据公式a cxabxa bci i i =将x 加进去，所以可以得出：e bxe axe abi i i =要想变成定轴传动，就要把x 放到上面去，所以这里就要运用第一个公式1=+c ba abc i i 了，所以)1()1(xbe xae e bxe axe abi i i i i --==所以现在eab i 就变成了两个定轴传动之间的关系式了。

定轴传动的传动比就好办了，直接写出来就可以了。

即)1()1())1(1())1(1()1()1(01ce b d a ec e b dc e a c xbe xae e bx e ax eab Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i i ⨯-+=⨯--⨯--=--== 再例如下面的传动机构：已知其各轮的齿数为z 1=100，z 2=101，z 2’ =100 ，z 3=99。

差速器行星齿轮自转转速计算
差速器是汽车传动系统中一个非常重要的部件，它可以将发动机的动力传递到车轮上。

差速器中的行星齿轮组自转也是其运转原理之一。

本文将介绍如何计算差速器行星齿轮组的自转转速。

首先，我们需要了解差速器行星齿轮组的结构。

它由太阳轮、行星轮、行星架和内环组成。

太阳轮位于中心，内环与车轮相连，行星轮则固定在行星架上。

当差速器运转时，太阳轮会驱动行星轮和行星架一起自转，同时行星架上的行星轮也会绕太阳轮旋转。

根据行星齿轮组的运动原理，我们可以得出以下公式：
V = (N1 - N2) / (N1 + N2) * V1
其中，V为车轮速度，N1、N2分别为太阳轮和内环的齿轮数，V1为发动机转速。

根据这个公式，我们可以求出差速器行星齿轮组的自转转速。

假设太阳轮和内环的齿轮数分别为20和25，发动机转速为
3000rpm，车轮速度为60km/h，则差速器行星齿轮组的自转转速为：
V = (20 - 25) / (20 + 25) * 3000rpm = -428.57rpm 这个负值表示行星齿轮组的自转方向与发动机的旋转方向相反。

需要注意的是，上述计算公式只适用于理论计算，实际差速器行星齿轮组的自转转速还会受到多种因素的影响，例如齿轮的磨损、摩擦等。

因此，在实际应用中需要结合实际情况进行调整。

行星齿轮齿隙计算
行星齿轮传动是一种常见的齿轮传动形式，通常包括太阳轮、行星轮、行星架、内齿圈等部件。

齿隙是指齿轮啮合时齿槽之间的间隙或缝隙。

在行星齿轮传动中，齿隙计算是很重要的，因为它影响着传动的精度、响应性以及噪声等性能。

齿隙计算涉及到一系列因素，其中一些因素包括：
模数（Module）：模数是用于描述齿轮的尺寸的参数，它是齿轮齿数与齿轮直径的比值。

在行星齿轮传动中，太阳轮、行星轮、内齿圈的模数通常会影响齿隙的大小。

压力角（Pressure Angle）：压力角是指齿轮齿面上的法线与从齿轮轴心引出的线之间的夹角。

压力角的大小也会对齿隙产生影响。

啮合角（Meshing Angle）：啮合角是指相邻齿轮齿槽之间的夹角。

齿轮的啮合角也会影响齿隙的大小。

制造精度：齿轮的制造精度、加工工艺以及材料的特性都会对齿隙产生影响。

齿隙的计算通常涉及到几何学、材料力学和制造工艺等多个方面的知识。

精确的齿隙计算对于确保行星齿轮传动的正常运行和性能优越性非常重要。

在设计和制造行星齿轮传动时，通常会遵循相关标准和规范，以确保齿隙的控制在合适的范围内。

行星齿轮传动比8个公式
1.齿轮比计算公式：
齿轮比=-(R+2)/(R+1)，其中R为行星轮的齿数。

2.行星轮直径公式：
行星轮的直径可以通过行星轮齿数来计算。

行星轮直径=齿数*模数。

3.太阳轮直径公式：
太阳轮的直径可以通过太阳轮齿数来计算。

太阳轮直径=齿数*模数。

4.行星轮轮齿厚度公式：
行星轮的轮齿厚度可以通过行星轮直径和模数来计算。

行星轮轮齿厚度=2*模数。

5.太阳轮轮齿厚度公式：
太阳轮的轮齿厚度可以通过太阳轮直径和模数来计算。

太阳轮轮齿厚度=2*模数。

6.行星齿轮传动的速度比公式：
速度比=齿数A/齿数B，其中齿数A为太阳轮齿数，齿数B为行星轮齿数。

7.行星齿轮传动的扭矩比公式：
扭矩比=(半径A/半径B)^2，其中半径A为太阳轮半径，半径B为行星轮半径。

8.行星齿轮传动的传动效率公式：
传动效率=输出功率/输入功率。

综上所述，行星齿轮传动的8个常用公式分别是齿轮比计算公式、行星轮直径公式、太阳轮直径公式、行星轮轮齿厚度公式、太阳轮轮齿厚度公式、行星齿轮传动的速度比公式、行星齿轮传动的扭矩比公式和行星齿轮传动的传动效率公式。

这些公式帮助工程师在设计和计算行星齿轮传动时能够准确地确定齿轮比、轮齿尺寸和传动性能等参数，从而提高传动系统的可靠性和效率。

行星齿轮转速比的计算涉及到多个因素，包括行星齿轮的结构、输入和输出转速、以及传动系统的其他部分。

以下是一个基本的计算过程，但请注意，实际情况可能会因具体的设计和参数而有所不同。

假设我们有一个简单的行星齿轮系统，其中有一个行星齿轮和一个太阳轮，并且我们已经知道输入转速（太阳轮的转速）和输出转速。

我们需要通过计算来得到行星齿轮的转速比。

首先，我们需要明确的是，行星齿轮的转速取决于太阳轮的转速。

这是因为在行星齿轮系统中，行星齿轮围绕太阳轮旋转。

所以，太阳轮的转速就决定了行星齿轮的转速。

我们设太阳轮的输入转速为n1，行星齿轮的输出转速为n2。

假设这个系统是处在理想状态下，没有摩擦和阻力，那么我们可以根据行星齿轮的运动学原理，得出n2 = n1 * R，其中R 是一个常数，表示行星齿轮与太阳轮的相对转动半径。

在许多实际应用中，这个R值是很难直接测量的。

但通常我们可以通过计算来近似得出。

行星齿轮的动力传输是通过齿轮间的啮合实现的，这个啮合的过程会影响到行星齿轮的运动速度。

当太阳轮的旋转使行星齿轮受到推力时，行星齿轮就会加速；反之，如果太阳轮停止旋转，行星齿轮就会减速。

这个减速的过程就是行星齿轮与太阳轮之间的相对转动半径变化的过程。

假设我们把这个过程看作是一个弹簧系统的振动过程，那么我们可以使用弹簧振动的公式来近似计算R。

弹簧振动的公式通常表示为弹簧系统的阻尼振荡过程，其中弹簧的弹性系数和阻尼系数会影响到振荡的速度和频率。

在行星齿轮系统中，我们可以把太阳轮看作是弹簧的一端，行星齿轮是另一端。

这个过程会影响到行星齿轮的转速。

所以，我们可以把行星齿轮的输出转速近似看作是输入转速和相关参数的函数，具体可以表示为：n2 = f(n1, R)。

这里的R需要用一些方式进行估算或测量。

在得到这个函数之后，我们就可以根据给定的输入转速n1和相应的参数R来求出行星齿轮的实际输出转速n2了。

这只是一个基本的计算过程，实际情况可能会因具体的行星齿轮设计、传动系统状态等因素而有所不同。

行星齿轮传动比计算在《机械原理》上,行星齿轮求解就是通过列一系列方程式求解,其求解过程繁琐容易出错,其实用不着如此,只要理解了传动比eab i 的含义,就可以很快地直接写出行星齿轮的传动比,其关键就是掌握几个根据e ab i 的含义推导出来公式,随便多复杂的行星齿轮传动机构,根据这几个公式都能从头写到尾直接把其传动比写出来,而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。

一式求解行星齿轮传动比有三个基本的公式1=+c ba a bc i i ――――――――――――――――――――――――1 a cx a bx abci i i = ―――――――――――――――――――――――――2 a cb abc i i 1= ――――――――――――――――――――――――――3熟练掌握了这三个公式后,不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。

关键就是要善于选择中间的一些部件作为参照,使其最后形成都就是定轴传动,所以这些参照基本都就是一些行星架等例如象论坛中“大模王”兄弟所举的例子:在此例中,要求出e ab i ＝？,如果行星架固定不动的话,这道题目就简单多了,就就是一定轴传动。

所以我们要想办法把e ab i 变成一定轴传动,所以可以根据公式a cx a bx a bci i i =将x 加进去, 所以可以得出:e bx e ax eab i i i =要想变成定轴传动,就要把x 放到上面去,所以这里就要运用第一个公式1=+c ba abc i i 了,所以)1()1(xbe x ae ebx e ax eab i i i i i --==所以现在eab i 就变成了两个定轴传动之间的关系式了。

定轴传动的传动比就好办了,直接写出来就可以了。

即)1()1())1(1())1(1()1()1(01c e bd ae c e b d c e a c x be x ae e bx e ax e ab Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i i ⨯-+=⨯--⨯--=--== 再例如下面的传动机构:已知其各轮的齿数为z 1=100,z 2=101,z 2’ =100 ,z 3=99。

行星齿轮传动比计算在《机械原理》上，行星齿轮求解是通过列一系列方程式求解，其求解过程繁琐容易出错，其实用不着如此，只要理解了传动比eab i 的含义，就可以很快地直接写出行星齿轮的传动比，其关键是掌握几个根据e ab i 的含义推导出来公式，随便多复杂的行星齿轮传动机构，根据这几个公式都能从头写到尾直接把其传动比写出来，而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。

一式求解行星齿轮传动比有三个基本的公式1=+c ba a bc i i ――――――――――――――――――――――――1 acx a bx abci i i = ―――――――――――――――――――――――――2 a cb abc i i 1= ――――――――――――――――――――――――――3熟练掌握了这三个公式后，不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。

关键是要善于选择中间的一些部件作为参照，使其最后形成都是定轴传动，所以这些参照基本都是一些行星架等例如象论坛中“大模王”兄弟所举的例子：在此例中，要求出e ab i ＝？，如果行星架固定不动的话，这道题目就简单多了，就是一定轴传动。

所以我们要想办法把e ab i 变成一定轴传动，所以可以根据公式a cx a bx a bci i i =将x 加进去， 所以可以得出：e bx e ax eab i i i =要想变成定轴传动，就要把x 放到上面去，所以这里就要运用第一个公式1=+c ba abc i i 了，所以)1()1(xbe x ae ebx e ax eab i i i i i --==所以现在eab i 就变成了两个定轴传动之间的关系式了。

定轴传动的传动比就好办了，直接写出来就可以了。

即)1()1())1(1())1(1()1()1(01c e bd ae c e b d c e a c x be x ae e bx e ax e ab Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i i ⨯-+=⨯--⨯--=--== 再例如下面的传动机构：已知其各轮的齿数为z 1=100，z 2=101，z 2’ =100 ，z 3=99。

行星齿轮减速比计算公式行星齿轮减速器是一种广泛应用于机械传动领域的高精度、高可靠性的减速装置。

其主要特点是结构紧凑、传动效率高、承载能力强、运转平稳、噪音低等优点，因此被广泛应用于各种工业设备中。

在行星齿轮减速器的设计和应用中，减速比是一个十分重要的参数，它直接影响到减速器的传动性能和使用效果。

因此，准确地计算行星齿轮减速比是十分关键的。

行星齿轮减速比的计算公式是基于行星齿轮传动原理和几何学原理推导而来的。

在此，我们将详细介绍行星齿轮减速比的计算公式及其应用。

一、行星齿轮传动原理行星齿轮传动是一种基于行星齿轮组的减速传动形式，其结构如图1所示。

图1 行星齿轮传动结构示意图行星齿轮传动由外齿轮、行星齿轮、内齿轮和行星架组成。

其中，外齿轮是固定不动的，内齿轮是输出轴，行星齿轮则绕行星架旋转。

当输入轴带动外齿轮旋转时，外齿轮的齿轮会带动行星齿轮绕内齿轮旋转，从而实现减速传动。

行星齿轮传动的减速比与行星轮齿数、太阳轮齿数和内齿轮齿数的关系式如下：i = (Zs + Zp) / Zp其中，i表示行星齿轮传动的减速比；Zs表示太阳轮的齿数；Zp表示行星轮的齿数。

二、行星齿轮减速比计算公式行星齿轮减速比的计算公式可以通过行星齿轮传动原理和几何学原理推导而来。

1. 求太阳轮的齿轮数太阳轮的齿轮数可以通过行星齿轮传动的几何关系求得。

如图2所示，在行星齿轮传动中，行星齿轮的中心距离与太阳轮的中心距离之比为：a /b = (Zs + Zp) / Zp其中，a表示行星齿轮的中心距离，b表示太阳轮的中心距离。

因此，太阳轮的齿数可以表示为：Zs = (a / b) × Zp / (1 - a / b)2. 求内齿轮的齿轮数内齿轮的齿轮数可以通过行星齿轮传动的几何关系和行星齿轮传动的减速比求得。

如图3所示，在行星齿轮传动中，内齿轮的齿数和太阳轮的齿数之比为：Zi / Zs = i / (i - 1)其中，i表示行星齿轮传动的减速比。

行星齿轮计算公式行星齿轮计算公式。

行星齿轮是一种常用于传动系统中的齿轮装置，其结构紧凑、传动比大、负载分布均匀等特点使其在工业生产中得到广泛应用。

在设计和选择行星齿轮传动系统时，需要根据具体的工程要求来计算传动比、载荷分布等参数，而行星齿轮的计算公式则是其中的关键。

一、行星齿轮的基本结构。

行星齿轮由太阳轮、行星轮、行星架和内齿圈组成。

太阳轮和内齿圈为固定不动，行星轮则围绕太阳轮旋转，行星架连接行星轮和内齿圈。

通过这种结构，行星齿轮可以实现较大的传动比，同时也可以实现负载的均匀分布。

二、行星齿轮的计算公式。

1. 传动比的计算公式。

行星齿轮的传动比可以通过以下公式来计算：i = (1 + Zs/Zp) (1 + Zs/Zr)。

其中，i为传动比，Zs为太阳轮的齿数，Zp为行星轮的齿数，Zr为内齿圈的齿数。

通过这个公式，可以很容易地计算出行星齿轮的传动比，从而为工程设计提供参考依据。

2. 载荷分布的计算公式。

行星齿轮的载荷分布是设计中需要重点考虑的问题之一。

通常情况下，可以通过以下公式来计算行星齿轮的载荷分布：Fp = Fr (Zs/Zp)。

其中，Fp为行星轮的载荷，Fr为内齿圈的载荷，Zs为太阳轮的齿数，Zp为行星轮的齿数。

通过这个公式，可以清晰地了解到行星齿轮在工作过程中的载荷分布情况，从而为传动系统的设计提供指导。

3. 功率传递的计算公式。

行星齿轮的功率传递可以通过以下公式来计算：P = (2 π n T) / 60。

其中，P为功率，π为圆周率，n为转速，T为扭矩。

通过这个公式，可以计算出行星齿轮在工作时所需的功率，为传动系统的选型提供依据。

4. 效率的计算公式。

行星齿轮的效率可以通过以下公式来计算：η = (1 ε) 100%。

其中，η为效率，ε为传动损失。

通过这个公式，可以清晰地了解到行星齿轮在工作时的能量损失情况，从而为传动系统的优化提供参考。

三、行星齿轮计算公式的应用。

行星齿轮的计算公式在工程设计中具有重要的应用价值。