一些素数个数计算

小学一年级数的素数练习题一、判断题（共10题，每题2分，共20分）1. 5是素数。

（）2. 12是素数。

（）3. 2是素数。

（）4. 7是素数。

（）5. 10是素数。

（）6. 3是素数。

（）7. 15是素数。

（）8. 13是素数。

（）9. 6是素数。

（）10. 1是素数。

（）二、选择题（共10题，每题3分，共30分）1. 下列哪个数是素数？A. 4B. 9C. 13D. 152. 下列哪个数不是素数？A. 7B. 11C. 10D. 23. 49是不是素数？A. 是B. 不是4. 下列哪个数是素数？A. 16B. 3C. 8D. 125. 下列哪个数不是素数？A. 5B. 2C. 6D. 116. 20是不是素数？A. 是B. 不是7. 下列哪个数是素数？A. 14B. 17C. 9D. 68. 下列哪个数不是素数？A. 7B. 4C. 23D. 199. 35是不是素数？A. 是B. 不是10. 下列哪个数是素数？A. 27B. 29C. 20D. 14三、填空题（共5题，每题4分，共20分）1. 11是不是素数？答：是2. 21是不是素数？答：不是3. 下列哪个数是素数？27、13、20、15答：134. 下列哪个数不是素数？19、10、3、8答：105. 33是不是素数？答：不是四、计算题（共5题，每题6分，共30分）1. 将所有小于20的素数写出来。

答：2, 3, 5, 7, 11, 13, 17, 192. 在1-30中有几个素数？答：10个3. 在1-50中有几个素数？答：15个4. 在1-100中有几个素数？答：25个5. 判断下列各数是否为素数：23、25、31、37、39答：23是素数，25不是素数，31是素数，37是素数，39不是素数五、解答题（共2题，每题10分，共20分）1. 请解答下列问题：a) 1是不是素数？为什么？b) 在所有正整数中，2是不是唯一的素数？答：a) 1不是素数。

素数姓名：学号：班级：数学与应用数学4班实验报告实验目的：素数(Prime)是构造所有数的“基本材料”，犹如化学上的化学元素和物理学中的基本粒子，有关素数的许多看似简单却极富刺激性的奇妙问题，向一代代数学家提出了挑战，始终吸引着他们的目光。

本实验将探讨素数的规律及其相关的某些有趣问题，如素数的判别，求素数的个数等。

实验环境：Mathematica软件实验基本理论和方法：素数：如果一个大于1的自然数只能被1及它本身整除，则该数称为素数，否则被称为合数。

算数基本定理：从数学史的黎明时期开始，数学家就一直在探索自然数的奥秘，远在古希腊时代，欧几里得就证明了每一个合数都可以分解为若干个素数的乘积，并且在不计较素数排列顺序时这种分解是唯一的，这就是所谓的算数基本定理。

算数基本定理表明素数是构造自然数的基石，正如物质的基本粒子一样。

Mathematica的素数函数：Mathematica系统提供了两个常用的与素数有关的函数：（1）[n]，就是返回从第一个素数2数起的第n个素数；（2）PrimeQ[n]，就是判断自然数n是否为素数，是则返回True，否则返回False。

使用系统函数输出某个指定范围内的所有素数，只要定义如下的函数即可：筛法求素数：2000多年前，希腊学者埃拉托色尼(Eratosthenes 公元前约284-192年)给出了一个寻找素数的简便方法—筛法：写下从2、3、…、N，注意到2是一个素数，划去后面所有2的倍数，越过2，第一个没有被划去的数是3，它是第二个素数，接下来再划掉所有3的倍数，3之后没有被划去的数是5，然后再划掉除5外所有5的倍数，以此类推。

显然，划掉的都是较小整数的倍数，它们都不是素数，都被筛掉了，而素数永远不会被筛掉，它们就是要寻找的不超过N的所有素数。

试除法求素数：假设我们已经找到了前n个素数，为了下一个素数我们从开始一次检验每一个整数N，看N是否能被某个整除。

如果N能被前面的某个素数整除，则N为合数，否则N即为下一个素数。

素数个数公式及有关猜想证明引理：若21=p ,32=p ，…j p …,i p ,为连续素数，1≤j ≤i,且j p | n ，1≤m ≤n ，则 m ≠0(mod j p ) 的数的个数)(n y i 可表示为∏=-⋅=ij ji p n n y 1)11()(. 证明：I.当i=1时,∵ 1p =2 , 1p |n ∴ )11()211(2)(11p n n n n n y -⋅=-⋅=-= 结论成立。

Ⅱ.假设i=k 时，结论成立，即：∏=-⋅=kj jk p n n y 1)11()( 成立。

当i=k+1时，∵ 1p |n ，2p |n ，…， k p |n ，据归纳假设 ∴ ∏=-⋅=kj jk p n n y 1)11()( 因为1+k p |n ，所以 m=o (mod 1+k p ) 的数有1+k p n个， 去了k p p p ,,,21 的倍数后，余 ∏=+-⋅kj jk p p n 11)11( 个 ∴ ∏∏=+=+-⋅--⋅=kj j k kj j k p p n p n n y 1111)11()11()()11()11(11+=-⋅-⋅=∏k kj j p p n ∏+=-⋅=11)11(k j j p n∴ i=k+1时，结论 ∏+=+-⋅=111)11()(k j jk p n n y 成立。

由I 、Ⅱ，当i 为任何正整数，结论都成立。

引理证毕。

定理1：（素数个数连乘积式公式）：若21=p ,32=p ，…k p …,i p为连续素数，0≤k ≤i 且k pn 的素数个数记为π(n)，则有公式π（n ）=2+ 221111()(1)k ik k k j j p p p λ+==⎡⎤--⎢⎥⎢⎥⎣⎦∑∏+g(n)其中g(n)满足：－)(1+i p π<g(n)< )(1+i p π,λ微单减。

证明： ∵ n ＝1+(4－1)+(9－4)+(25－9)+…+)(221k k p p -++…+)(2i p n - 区间 (212,+k k p p )的整数去掉21=p ,32=p ，…k p 的倍数后，余下全为素数。

实验名称计算出1000以内10个最大素数之和实验目的1、熟练掌握if、if…else、if…else if语句和witch语句格式及使用方法，掌握if语句中的嵌套关系和匹配原则，利用if语句和switch语句实现分支选择结构。

2、熟练掌握while语句、do…while语句和for语句格式及使用方法，掌握三种循环控制语句的循环过程以及循环结构的嵌套，利用循环语句实现循环结构。

3、掌握简单、常用的算法，并在编程过程中体验各种算法的编程技巧。

进一步学习调试程序，掌握语法错误和逻辑错误的检查方法。

实验内容计算并输出1000以内最大的10个素数以及它们的和。

要求：在程序内部加必要的注释。

由于偶数不是素数，可以不考虑对偶数的处理。

虽然在1000以内的素数超过10个，但是要对1000以内不够10个素数的情况进行处理。

输出形式为：素数1＋素数2＋素数3＋…＋素数10＝总和值。

算法描述流程图Main函数：判断素数：源程序#include#includeint sushu(int n)/* 判断素数的函数*/{int t,i;t=sqrt(n);for(i=2;i<=t;i++)if(n%i==0)/* 如果不是素数，返回0 */return 0;return n;/* 如果是素数，返回该数*/}void main(){int i,j=0,n,m=0,a[1000],x;/*clrscr();*/printf("Please input a number form 1 to 1000:"); scanf("%d",&x);if(x==2)/* x=2时的处理*/printf("%d\n",x);else if(x<=1) /* x在1～1000范围外时的处理*/ printf("Error!\n");else{if(x%2==0)/* x为偶数时，把x变为奇数*/x--;for(i=x;i>1;i-=2)/* x为奇数时，做函数计算*/ {n=sushu(i); /* 做判断素数的函数调用*/if(n!=0)/* 对素数的处理*/{a[j]=n;/* 把素数由大至小存入数组a[ ]中*/（转载自第一范文网，请保留此标记。

费马小定理素数判定蒙哥马利算法(强烈推荐）2009-11-07 12:42费马小定理素数判定蒙哥马利算法约定：x%y为x取模y，即x除以y所得的余数，当x<y时，x%y=x，所有取模的运算对象都为整数。

x^y表示x的y次方。

乘方运算的优先级高于乘除和取模，加减的优先级最低。

见到x^y/z这样，就先算乘方，再算除法。

A/B，称为A除以B，也称为B除A。

若A%B=0，即称为A可以被B整除，也称B可以整除A。

A*B表示A乘以B或称A乘B，B乘A，B乘以A……都TMD的一样，靠！复习一下小学数学公因数：两个不同的自然数A和B，若有自然数C可以整除A也可以整除B，那么C就是A和B的公因数。

公倍数：两个不同的自然数A和B，若有自然数C可以被A整除也可以被B整除，那么C就是A和B的公倍数。

互质数：两个不同的自然数，它们只有一个公因数1，则称它们互质。

费马是法国数学家，又译“费尔马”，此人巨牛，他的简介请看下面。

不看不知道，一看吓一跳。

/BasicStudy/LearnColumn/Maths/shuxuejiashi/j12.htm费马小定理：有N为任意正整数，P为素数，且N不能被P整除（显然N和P互质），则有：N^P%P=N(即：N的P次方除以P的余数是N)但是我查了很多资料见到的公式都是这个样子：(N^(P-1))%P=1后来分析了一下，两个式子其实是一样的，可以互相变形得到，原式可化为：(N^P-N)%P=0(即：N的P次方减N可以被P整除，因为由费马小定理知道N的P次方除以P的余数是N)把N提出来一个，N^P就成了你N*(N^(P-1))，那么(N^P-N)%P=0可化为：(N*(N^(P-1)-1))%P=0请注意上式，含义是：N*(N^(P-1)-1)可以被P整除又因为N*(N^(P-1)-1)必能整除N（这不费话么!）所以，N*(N^(P-1)-1)是N和P的公倍数，小学知识了^_^又因为前提是N与P互质，而互质数的最小公倍数为它们的乘积，所以一定存在正整数M使得等式成立：N*(N^(P-1)-1)=M*N*P两边约去N，化简之：N^(P-1)-1=M*P因为M是整数，显然：(N^(P-1)-1)%P=0即：N^(P-1)%P=1============================================积模分解公式先有一个引理，如果有：X%Z=0，即X能被Z整除，则有：(X+Y)%Z=Y%Z这个不用证了吧...设有X、Y和Z三个正整数，则必有：(X*Y)%Z=((X%Z)*(Y%Z))%Z想了很长时间才证出来，要分情况讨论才行：1.当X和Y都比Z大时，必有整数A和B使下面的等式成立：X=Z*I+A（1）Y=Z*J+B（2）不用多说了吧，这是除模运算的性质！将（1）和（2）代入(X*Y)modZ得：((Z*I+A)(Z*J+B))%Z乘开，再把前三项的Z提一个出来，变形为：(Z*(Z*I*J+I*A+I*B)+A*B)%Z（3）因为Z*(Z*I*J+I*A+I*B)是Z的整数倍……晕，又来了。

计算区间素数和c语言pta区间素数和是指给定两个正整数A和B（A≤B），求出A到B之间所有的素数之和。

素数是指大于1且只能被1和自身整除的数。

为了计算区间素数和，我们首先需要了解什么是素数。

在数学中，素数也称质数，是指大于1且只能被1和自身整除的整数。

常见的素数有2、3、5、7、11等。

例如，2是最小的素数，而1不是素数，因为它只有一个因数。

在计算区间素数和时，我们可以采用一种常用的算法——埃拉托斯特尼筛法（也称为筛法）。

这个算法的思想是从小到大依次遍历所有自然数，将能被当前数整除的数标记为合数，并将其排除。

这样，最终会得到一串素数。

现在，让我们使用C语言来实现计算区间素数和的程序。

首先，我们需要定义两个变量A和B，表示区间的起始值和结束值。

然后，我们可以编写一个函数来判断一个数是否为素数，以便后续的计算。

```cinclude<stdio.h>int isPrime(int num){int i;for (i = 2; i < num; i++){if (num % i == 0){return 0;}}return 1;}int main(){int A, B, i, sum;printf("请输入区间的起始值A："); scanf("%d", &A);printf("请输入区间的结束值B："); scanf("%d", &B);sum = 0;for(i = A; i <= B; i++){if(isPrime(i)){sum += i;}}printf("区间素数和为：%d\n", sum);return 0;}```以上代码中，我们定义了一个名为isPrime的函数，用于判断一个数是否为素数。

在main函数中，我们首先从用户处获取区间的起始值A和结束值B。

比例法证明没有最大的孪生素数本文证明的方法是将奇数从小到大划分成若干个阶段，每个阶段的起始数是一个奇数的完全平方数。

从2到7共4个奇数为第一阶段。

当然素数2不是奇数也不是完全平方数就不用讨论了。

从9到23共8个奇数为第二阶段。

25至47共12个奇数为第三阶段（如表1）。

下表1中第一列为奇数列，从小到大按顺序排列。

在奇数列的任何一个奇数的行如果没有除数就是素数，相邻两行的除数列都是空的就产生了孪生素数。

例如第5阶段的奇数103的行的横向除数列是空的没有除数，哪么103就是素数。

奇数101、103两个数的除数行中没有除数，哪么这两个奇数就是孪生素数。

奇数105行的除数列有3、5、7共3个除数。

哪么105就是合数。

除数列中如果有合数的除数，就不要计算在内，可以去除。

例如下表1中的除数9全部和除数3是同一行中，就没有必要计算到除数9。

例如除数15、21、25……等都是合数，都不要统计到除数列内。

从下表1中可以看出，素数的排列受除数排列的影响，整体上从小到大基本上素数的占比是均匀的变化，有规律的变化的。

本文计算思路是算出每个阶段素数和孪生素数的占有比例，来求证出无限大阶段中孪生素数存在的比例。

经过计算得出的结论是如果阶段数越大，阶段中的奇数的数量就会越多，虽然孪生素数占有比例会越来越小，但平均每个阶段中孪生素数不小于2对，来证明出没有最大的孪生素数。

例如第3阶段从25到47共12个奇数，不仅有能被除数3整除的数，还有能被除数5整除数。

从下表1中的3阶段可以看出，只要除数3和5覆盖不上的行数就是素数，除数3没有覆盖的行数有23，除数5没有覆盖的行数有45。

第3阶段素数占有的比例计算如下；式1 ；23X45=815第三阶段素数个数计算：式2；815X12=6.39(个)每个阶段的素数比例公式；式3；23X45X67 (X)2N−22N−1= 阶段中的素数比例式中；N——阶段数需要注意的是当式3中如果乘到有合数分母的分数时可以省略不要乘了。

梅森素数梅森素数素数也叫质数，是只能被自己和1整除的数，如2、3、5、7、11等。

2300年前，古希腊数学家欧几里得证明了素数有无穷多个，并提出少量素数可写成“2p-1”的形式，这里的指数p也是一个素数。

由于这种素数具有许多独特的性质和无穷的魅力，千百年来一直吸引着众多的数学家和无数的业余数学爱好者对它进行探究。

可能你还是不太了解，那就再详细点。

了解梅森素数还记得你小学时背诵的素数表吗？那时候它还叫做质数表“2、3、5、7……”如今你是否已经真正理解了老师说过的话：这些只能被1和本身整除的数，具有着无穷的魅力。

还记得你中学时计算的2的整数幂吗？计算机时代，作为二进制的体现，它们正大行其道。

“2、4、8、16、32、64、128、256……”十多年来，电脑内存的容量正是经历了这些熟悉的数字，直到现在的2048M（2G）以及更多。

现在，让我们从这些2的整数幂中挑出以素数为指数的，再把它减1，试试看会发现什么？22－1＝3、23－1＝7、25－1＝31、27－1＝127……嗯，你的心是不是激动起来了？一个伟大的发现似乎就在眼前……别急别急，你的发现很妙，只是有些儿惋惜……你已经迟到了二千年。

在2300多年前，古希腊的数学家，那位写出不朽的《几何原本》的欧几里得在证明了素数有无穷多个之后，就顺便指出：有许多素数可以写成2P－1的形式，其中指数P也是素数。

很容易想到，刚才你所发现的22－1、23－1、25－1、27－1正是其中排列最前的4个！当P＝11、13、17、19、23……的时候，2P－1还是素数吗？到底有多少这种2P－1型的素数呢？在计算能力低下的公元前，这个关于素数的探寻之旅就已经吸引了无数的人。

人们唯独对素数如此着迷不是没有理由的，它有着许多简单而又美丽的猜想，有的已经成为定理，而有的则至今还没有答案。

例如著名的哥德巴赫猜想，让人们苦苦追索：是否任何一个大于或等于6的素数，都可以表示为两个奇素数的和？再比如孪生素数问题所提出的：像5和7、41和43这样相差2的素数，到底有多少对呢？在数学史上起个大早的古希腊人还有许多关于素数的发现，完美数就是其中之一。

一些素数个数计算一、欧几里得素数概念：都是整数，其形式为En=Pn+1,其中Pn是Pn的质数阶乘。

前几个欧几里得数 3 7 31 211 2311 30031510511……因为是En=Pn+1,数列中的项差分布与自然数数列项差分布不同，所以，就不能用求自然数数列的奇质数方法计算。

根据欧几里得数的阶乘性质和素数个数分布与计算原理，每一个欧几里得数是否奇质数，只能单独计算。

根据欧几里得数的性质，第1、2、3项欧几里得数不可能有因子，只能是奇质数;第4项211 因子可能是11和13，不可能是2、3、5、7以及》17的奇质数，所以第4项是奇质数的可能性为1X 10/11 X 12/13〜0.839，以后以此类推。

欧几里得素数总个数计算公式F=1 （第1项）+1 （第2项）+1 （第3项）+1X 10/11 X 12/13 （第4 项）+1X12/13X16/17X18/19X22/23X28/29X30/31X36/37X40 /41 X42/43 X 46/47 （第5 项）+……随着欧几里得数的不断增大，F也不断缓慢增大，所以，欧几里得素数有无限个。

以上的单个计算方法，适合于随机抽取（项差不遵从自然数数列项差分布规律）的一组数列和自然数数列的奇质数个数计算。

项数越多，计算值越准确。

二、费马素数概念：形式为2n+1 （n=2m m取值为0、1、2、3……则n 为1、2、4、8……）前几个费马数是3、5、17、257、65537、4294967297 ••…求其中的素数个数。

从上面可以看出，项差不符合自然数数列分布规律，费马数数列只是2k+1 （k取值为0、1、2、3……）数列中的一部分，可以参照上面的欧几里得素数素数计算方法求解。

当〜1、2、4、8、16……2n数时，叫做非费马数。

非费马数都可以进行因式分解，所以，非费马数都是合数，因子是绝大多数奇质数。

以上可以得出结论，费马数是非费马数的因子，而非费马数中除费马数因子之外的因子不可能是费马数的因子。

计算质数的公式有很多种，以下是一些常见的方法：
1.试除法：对于一个大于等于2的正整数n，从2开始到根号n为止依次试除n，若都不能整除，则n是质数。

2.埃氏筛法：先将2~n之间的数全部写出来，然后将其中最小的质数2的倍数（除了2自己）标记成合数，再找到下一个未被标记的数p（p>2），把它的倍数都标记成合数。

重复以上步骤直到p^2>n时才停止，那么此时所有未被标记为合数的数就是质数。

3.欧拉筛法：先按埃氏筛法筛选出质数，但在标记合数时不仅仅只用当前素数的倍数，而是将每个合数都标记了且只标记一次。

相比埃氏筛法，其时间复杂度更低。

ler-Rabin素性检验：该方法不是一种准确求解质数的算法，而是用随机算法对数进行检测是否可能为质数。

简单来说，如果一个大数n是质数，那么在模n意义下，a^(n-1) ≡1 (mod n)，其中a为小于n的任意一个正整数。

该方法的时间复杂度接近O(k log^3 n)，其中k为检验次数，通常要求k≥10。

注：以上算法均有优化方式，可进一步提高效率。

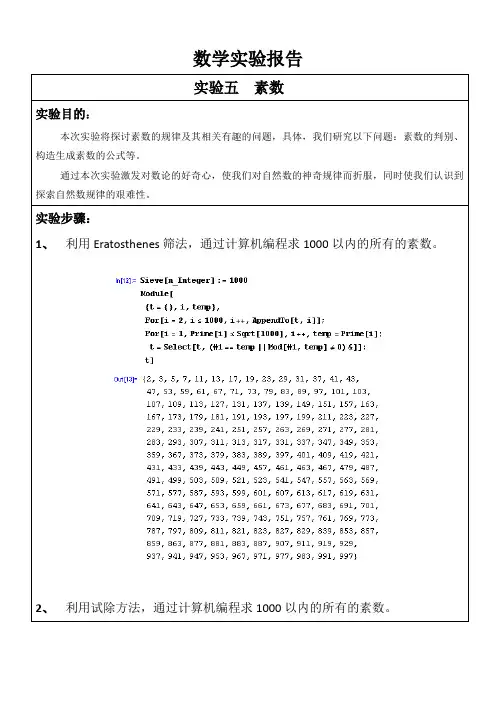
数学实验报告实验五素数实验目的：本次实验将探讨素数的规律及其相关有趣的问题，具体，我们研究以下问题：素数的判别、构造生成素数的公式等。

通过本次实验激发对数论的好奇心，使我们对自然数的神奇规律而折服，同时使我们认识到探索自然数规律的艰难性。

实验步骤：1、利用Eratosthenes筛法，通过计算机编程求1000以内的所有的素数。

2、利用试除方法，通过计算机编程求1000以内的所有的素数。

3、计算所有小于等于n的素数的个数。

（n=1000，10000）n=1000时，程序如右：]Pr imePi[1000运行结果：168n=10000时，程序如右：][Pr imePi10000运行结果：12294、计算b a被n整除所得的余数。

（a=2，b=7，n=6）和（a=3，b=5，n=48）n=6时,程序如右：]6,7,2[PowerMod运行结果： 2n=48时,程序如右：]48,5,3[PowerMod运行结果： 35、判断Mersenne数的素性。

程序如下:False]]] T rue, 0, If[u M]];2, - Mod[u^2 u ,i 1,-n i 1, For[i 1; -n 2^ M False,PrimeQ[n], If[! 4},u i, {M, Module[: _Integer]Mersenne[n ===++<==== 当n=127时，输出结果: True当n=48时，输出结果： False6、 令dx x n Li n ⎰=2log 1)(，!)(log )1(11)(1k n k k n R k k ∑∞=++=ζ，其中⋯+++=k k k 31211)(ζ。

试对一系列充分大的n,计算),(n π),log(/n n ),083660.1)/(log(-n n ).()(n R n Li 及其中哪一个公式最接近)(n π？程序如下：100000}] 900000, 100000, {i, [i],Do[Compare ]Print[t]R];,AppendT o[t Li];,AppendT o[t ;1.08366)]] - 100000] Log[E,N[100000/( ,AppendT o[t 100000]]];og[E,N[100000/L ,AppendT o[t 0000]];PrimePi[10 ,AppendT o[t ;Infinity}] 2, {k, l[k],k/Factoria 100000]^ Log[E,*1] eta[k NSum[1/k/Z1 R 100000}];2, {x, x],[1/Log[E,NIntegrate Li {}},t k, Module[{x,100000: Integer]Compare[n_++====运行结果：9592, 8685.89, 9588.4, 9628.76, 9580.43观察得到最接近)(n π的是)083660.1)/(log(-n n 。

众所周知，素数也叫质数，是只能被1和自身整除的数，如2、3、5、7、11等等。

2300年前，古希腊数学家欧几里得就已证明素数有无穷多个，并提出一些素数可写成“2p-1”的形式，这里的指数p也是一个素数。

这种特殊形式的素数具有独特的性质和无穷的魅力，千百年来一直吸引着众多的数学家(包括数学大师费马、笛卡尔、哥德巴赫、欧拉、高斯、哈代等)和无数的业余数学爱好者对它进行探究。

而17世纪法国数学家、法兰西科学院奠基人马林•梅森是其中成果较为卓著的一位，因此后人将“2p-1”型的素数称为“梅森素数”。

迄今为止，人类仅发现47个梅森素数。

由于这种素数珍奇而迷人，它被人们称为“数学珍宝”。

梅森素数历来是数论研究的一项重要内容，也是当今科学探索的热点和难点之一。

貌似简单探究极难梅森素数貌似简单，但探究难度却极大。

它不仅需要高深的理论和纯熟的技巧，而且还需要进行艰巨的计算。

1772年，有“数学英雄”美名的瑞士数学大师欧拉在双目失明的情况下，靠心算证明了231-1(即2147483647)是第8个梅森素数。

这个具有10位的素数，堪称当时世界上已知的最大素数。

欧拉的顽强毅力与解题技巧令人赞叹不已；法国大数学家拉普拉斯说的话，或许可以代表我们的心声：“读读欧拉，他是我们每一个人的老师。

”在“手算笔录”的年代，人们历尽艰辛，仅找到12个梅森素数。

而计算机的产生加速了梅森素数探究进程。

1952年，美国数学家拉婓尔•鲁滨逊等人使用SWAC型计算机在短短的几个月内，就找到了5个梅森素数：2521-1、2607-1、21279-1、22203-1和22281-1。

探究梅森素数不仅极富挑战性，而且对探究者来说有一种巨大的自豪感。

1963年6月2日晚上8点，当第23个梅森素数211213-1通过大型计算机被找到时，美国广播公司(ABC)中断了正常的节目播放，在第一时间发布了这一重要消息。

而发现这个素数的美国伊利诺伊大学数学系全体师生感到无比骄傲，为了让全世界都分享这一重大成果，以至把所有从系里发出的信封都盖上了“211213-1是个素数”的邮戳。

( n ) 时，π ( n, r ) = j + 1 。这个结论很好理解，从自然数列 1、2、3……
又因为
⎡n⎤ m ⎡ n ⎤ m ⎡ n ⎤ j = n−∑⎢ ⎥+∑⎢ ⎥− ∑ ⎢ ⎥+ p p p p p < < i =1 ⎣ pi ⎦ i< j ⎢ i j k ⎥ ⎢ ⎣ i j⎦ ⎣ i j k⎥ ⎦
m
⎡ n ⎤ m ⎡ n ⎤ ⎡n⎤ n−∑⎢ ⎥+∑⎢ ⎥− ∑ ⎢ ⎥+ i =1 ⎣ pi ⎦ i< j ⎣ ⎢ pi p j ⎦ ⎥ i< j<k ⎣ ⎢ pi p j pk ⎦ ⎥
倍数的个数也就是还剩有质数，合数和 1。故
⎡n⎤ m ⎡ n ⎤ m ⎡ n ⎤ n−∑⎢ ⎥+∑⎢ ⎥− ∑ ⎢ ⎥+ p p p p p < < i =1 ⎣ pi ⎦ i< j ⎢ i j k ⎥ ⎢ ⎥ ⎣ i j⎦ ⎣ i j k⎦
m
当 m = 0 时，有容斥原理可以知道这个公式表示 n 减去 n 以内 0 个质数倍数的个 数也就是没有减去一个数。故
pm 为 n 的前部素数， m = π
( n ) 是前部质数的个
数，那么所有不大于 n 的素数的个数
π ( n) = m + n − ∑ ⎢
⎡ n ⎤ ⎡ n ⎤ ⎡n⎤ ⎥− ∑ ⎢ ⎥+ ⎥ +∑⎢ p p p p p < < i =1 ⎣ pi ⎦ i< j ⎢ i j k ⎥ ⎢ ⎥ i j i j k ⎣ ⎦ ⎣ ⎦
素数的个数公式
作者姓名：弯国强
作者地址：漯河市舞阳县莲花镇第二初级中学 E-mail：632158@

素数普遍公式目录[隐藏]一、引言二、素数普遍公式三、素数的个数四、公式的用途五、素数普遍公式在认识形成中的作用和意义思考题一、引言二、素数普遍公式三、素数的个数四、公式的用途五、素数普遍公式在认识形成中的作用和意义思考题[编辑本段]一、引言2000多年前欧几里德在证明素数无穷多时就埋下了寻求素数普遍公式的伏笔素数普遍公式，以布劳维尔为首的直觉主义学派认为：“你没有给出第n个素数是如何构造的，就不能算是好的证明”。

2000多年来，数论学最重要的一个任务，就是寻找素数普遍公式，为此，一代又一代数学精英，耗费了巨大的心血，始终未获成功。

黎曼曾想用他的ζ函数数的“零点”来逼近素数普遍公式，至今未获成功。

也有人反向思考，用素数普遍公式逼近“零点”来解决黎曼猜想。

希尔伯特在1900年的国际数学家大会上说：对黎曼公式进行了彻底讨论之后，或许就能够严格解决哥德巴赫问题和孪生素数问题。

实际在哲学上，只要有一个明确的定义，就应该有一个公式。

[编辑本段]二、素数普遍公式公元前250年同样是古希腊的数学家埃拉托塞尼提出一种筛法：（一）“要得到不大于某个自然数N的所有素数，只要在2---N中将不大于√N的素数的倍数全部划去即可”。

（二）将上面的内容等价转换：“如果N是合数，则它有一个因子d满足1<d≤√N”。

（《基础数论》13页，U杜德利著，上海科技出版社）。

.（三）再将（二）的内容等价转换：“若自然数N不能被不大于(根号)√N的任何素数整除，则N是一个素数”。

见（代数学辞典[上海教育出版社]1985年。

屉部贞世朗编。

259页）。

（四）这句话的汉字可以等价转换成为用英文字母表达的公式：N=p1m1+a1=p2m2+a2=......=p k m k+a k 。

(1)其中p1，p2，.....，p k表示顺序素数2，3，5，,,,,。

a≠0。

即N不能是2m+0，3m+0，5m+0，...，p km+0形。

若N<P（k+1）的平方[注：后面的1，2，3，....，k，（k+1）是脚标，由于打印不出来，凡字母后面的数字或者i与k都是脚标] ，则N是一个素数。

素数的计算方式
素数，也叫质数，是指只能被1和自身整除的正整数，如2、3、5、7、11等。

计算素数的方法有很多种，以下介绍一些常见的方法。

1.试除法：试除法是最简单的一种判断素数的方法，即对于一个数n，只需用从2到√n的所有整数去除一遍n，如果都不能整除，则n为素数。

但是试除法的缺点是当n非常大时，需要判断的数也相应增加，计算量非常大。

2. 埃拉托色尼筛法：埃拉托色尼筛法是一种可以找出一定范围内素数的高效算法。

该算法的基本思想是：从2开始到n，所有的数都标记为素数，然后从2开始，将每个素数的倍数标记为合数，直到所有小于n的素数都被标记。

这样，未被标记的数即为素数。

该算法的时间复杂度为O(nloglogn)，比试除法要快很多。

3. 米勒-拉宾素性检验：米勒-拉宾素性检验是一种概率性的素性测试算法。

该算法的基本思想是利用费马小定理：如果p是素数，那么对于所有的a，a^(p-1) ≡1(mod p)。

该算法的步骤是：先把n-1分解成2^k * q的形式，然后随机选择a(2≤a≤n-2)并计算a^q mod n，如果结果为1或者n-1，则n极有可能是素数，否则继续计算a^2q, a^4q, …, a^(2^(k-1)q)，若其中某一项为n-1，则n也有可能是素数；
若所有计算结果都不是1或n-1，则n一定不是素数。

该算法的时间复杂度为O(k * log^3n)，是一种较快的素性测试算法。

以上是一些常见的计算素数的方法，当然也有更多其他的方法，选择适合的方法取决于具体的应用场景和需求。

11–20各数的认识引言在我们的日常生活中，我们经常会遇到11到20之间的数。

这些数字不仅仅是我们学习数学的基础，还在我们的生活中扮演着重要的角色。

本文将介绍11到20之间的数的一些基本概念和应用。

1111是一个素数，它只能被1和它自己整除。

在十进制系统中，它是一个两位数，由两个数字1组成。

11在数学中有一些独特的性质，比如11的平方是121，而它的立方是1331。

此外，11也是一个斐波那契数列中的数字，该数列由前两个数字相加而得到。

1212是一个非常有用的数，因为它可以被2、3、4和6整除。

这使得12在我们的日常生活中非常常见。

我们的钟表以12小时为一轮，一年有12个月，每天有两个12小时。

12还是一个高度合数，并且有许多实际应用，比如时间、几何等。

1313是一个素数，它是一个谐波数，和它的倒数相加等于1。

13是一个不可约分数，也就是它在分数中不能化简。

此外，13还在数学迷信中有特殊的地位，被认为是一个不吉利的数字。

这种迷信源于13人的最后的晚餐，以及一些历史事件的不详之处。

1414是一个偶数，可以被2整除。

它也是一个合数，可以被1、2、7和14整除。

14在我们的日常生活中比较常见，在一周中有两个14天，也就是两个星期。

14还可以被用来表示一年中的两个7天，也就是两个星期。

1515是一个奇数，不能被2整除。

它可以被3和5整除，是一个合数。

15还有一个特殊的性质，它可以表示为16进制中的F。

16进制是一种数学表示法，其中使用了16个数字，包括0-9和A-F。

15在计算机科学中起着重要的作用，因为它是一个2的幂次。

1616是一个2的幂次，它可以表示为2的4次方。

这使得16在计算机科学中非常常见，因为计算机使用二进制表示数值，并且16在二进制中是10000。

16也在我们的日常生活中有重要的意义，比如我们的钟表以16进制表示小时。

1717是一个素数，它不能被任何其他数字整除。

这使得17在密码学和计算机科学中非常有用，因为它可以用作加密算法和哈希函数的基础。

求素数公式公式之比较李君池内容提要“李君池求素数公式”的诞生，完美地解决了“找出好的求素数公式”这一“世界难题”。

虽然从古至今，在数论领域人们创造了若干个“求素数公式”，但没有一个“好的”“求素数公式”能让数论工作者用起来得心应手。

为了让读者朋友深刻感受“李君池求素数公式”的出色与完美，文章列举了“埃拉托斯特尼筛法”、“素数定理”、“素数生成公式”以及“素数计算公式”等几个著名的“求素数公式”与之相比较。

对于这几个人人敬仰的公式，本文没有作过多的点评，只是以展示为主，主要目的是让读者朋友们来评价“李君池求素数公式”与这几个著名公式相比较时的孰优孰劣。

关键词李君池求素数公式埃拉托斯特尼筛法素数定理素数生成公式素数计算公式2000多年前{HYPERLINK "/wiki/欧几里德"|欧几里德在证明素数无穷多时就埋下了寻求普遍公式的伏笔，以布劳维尔为首的直觉主义学派认为：“你没有给出第n个素数是如何构造的，就不能算是好的证明”。

2000多年来，数论学最重要的一个任务，就是寻找素数普遍公式，为此，一代又一代数学精英，耗费了巨大的心血，始终未获成功。

曾想用他的ζ函数数的“零点”来逼近素数普遍公式，至今未获成功。

也有人反向思考，用素数普遍公式逼近“零点”来解决。

在1900年的上说：对黎曼公式进行了彻底讨论之后，或许就能够严格解决哥德巴赫问题和孪生素数问题。

实际在哲学上，只要有一个明确的定义，就应该有一个公式。

一、李君池求素数公式自“世界上第一个求素数公式”一文成稿之后，我查阅了很多数论中有关“求素数公式”方面的著作及相关文章，特别是在互联网上，我搜索查寻了大量的关于“求素数公式”的内容，发现：至今还没有一个“好的”“求素数公式”的出现。

“李君池求素数公式”确实无愧于当今“世界上第一个求素数公式”这一称号。

她的诞生能否会给整个数论领域带来变化和变革，对此，我充满了期待和自信；人们能否深刻理会、理解“李君池求素数公式”中所蕴含的、丰富的内涵，人们在数论研究中是否会逐步推广、采用、利用“李君池求素数公式”来解决相关的数论问题，对此，我拭目以待。