2018解三角形课件高三复习课

专题 3：三角函数与解三角形问题归类篇类型一：同角三角函数求值一．前测回忆1．(1)假设sinα＝－5，且α为第四象限角，那么 tanα的值等于_____________ ．135答案：－12．2〔 2〕 tan ＝ 2，那么sin cos ＋ cos 2＝， sin 2－2sin cos ＋ 2＝．2sin cos ＋ sin3答案：8； 2．(3) sinα＋ cosα＝1，α∈ (0 ，π)，那么 cosα－ sinα＝， tanα＝．57 4 答案：－5；－3解析： sinα＋ cosα＝1，α∈ (0，π)，且 sin2α＋cos2α＝ 1，得到 sinα＝4， cosα＝－3 555二、方法联想1．三角函数求值(1) 知一求其余三角函数值；(2) 关于 sinα与 cosα的齐次式，同除cos 或 cos2，如果不是齐次，借助1＝ sin2α＋ cos2α构造齐次．(3)sinα＋ cosα， sinα－ cosα， sinαcosα间关系式注意根据角的范围确定三角函数值正负．无法确定正负时可根据三角函数值的正负(或与特殊角的三角函数值 )缩小角的范围．三、归类稳固*1 ． sinα＝4，并且α是第二象限角，那么 cosα的值为．5(三角函数正弦值，求余弦值)3答案：－．3π**2 ． tanα＝ 3，且π＜α＜2，那么 cosα－ sinα＝．〔三角函数正切值，求正弦、余弦值〕答案：10．5解析：sinα2＝ 3 且 sin2α＋ cos α＝ 1，得到 sinα与 cosα的值．cosα***3 ．假设 cosα＋ 2sinα＝－5，那么 tanα＝．(构造方程组求解sin α，cosα)答案： 2．解析：结合sin2α＋ cos2α＝ 1，得到 sinα与 cosα的值．类型二：三角函数的图像与性质一、前测回忆1．〔 1〕函数 y＝sin(2x－3 )的定义域为．答案： [kπ＋π2π6， kπ＋3 ](k∈Z )．π〔 2〕函数 y＝ sin(2x＋6 )， x∈ [0，3]的值域为．答案： [－12，1] ．〔 3〕＞ 0，在函数 y＝2sin x 与 y＝ 2cos x 的图像的交点中，距离最短的两个交点的距离为 2 3，那么的值为．π答案：2．〔 4〕函数 y＝ 2cos(3x－)单调减区间为．32k π π 2k π 4π答案： [＋ ，＋]( k ∈ Z )．3 9 3 9〔 5〕函数 y ＝ sin(2x ＋ 4 ) 的对称轴为 ；中心对称点为．答案： x ＝k π πk π π2＋ (k ∈ Z )； (2－ ， 0)(k ∈ Z )；882．〔 1〕函数 y ＝ 2sin 2x ＋ 3sinxcosx ＋3cos 2 x 的值域为．1 5答案： [ 2， 2]．〔 2〕函数 y ＝ 4sin 2x － 12cosx － 1， x ? [π 2π．－ ，] 的值域为63答案： [ －13， 8]．〔 3〕函数 y ＝ sinx ＋ cosx ＋ 2sinxcosx ＋ 2, x ? [0， π]的值域为．答案： [ 3， 3＋ 2]．4sinx ＋1 的值域为．〔 4〕函数 y ＝ cosx － 1答案： [0，＋ ∞)．提示：方法一：看作斜率，数形结合处理；方法二：导数法处理．π ．3．〔 1〕函数 y ＝Asin(2x ＋ φ)的对称轴为，那么 φ的值为x ＝6π答案： k π＋ 6(k ∈ Z )．〔 2〕函数y ＝ cos(2x ＋φ)为奇函数，求 φ的值为 ．π答案： k π＋ 2(k ∈ Z )．二、 方法联想1．三角函数的定义域方法：根据式子有意义的条件，列不等式组，解不等式求定义域．2．三角函数的值域方法 1：转化为 y ＝Asin(ωx＋ φ)形式，先求 ωx＋ φ的范围，再根据正弦函数的图象求出值域如 y ＝ asin 2ωx＋bsin ωx cos ωx＋ ccos 2ωx 的形式，先利用降幂公式化为一次形式，将用辅助角公式化为y ＝ Asin(2ωx＋φ)形式求值域．方法 2：利用换元法转化为二次函数值域问题．22如 :含有 sin x ，cosx(或 sinx) 和 cos x ， sinx(或 cosx)形式；含有 sinx ±cosx ， sinxcosx ： 形如分子、分母含有sinx ， cosx 的一次形式：方法 1：化为 sin(ωx＋ φ)＝ M 形式，再得用三角函数的有界性 (|sinx| ≤1，|cosx| ≤1)求值域．方法 2：导数法3．三角函数对称问题方法：对于函数 y ＝ Asin(ωx＋ φ)或 y ＝Acos(ωx＋ φ)假设 x ＝ x 0 为对称轴 f(x 0)＝ ±A ．若 (x 0， 0)为中心对称点f(x 0)＝ 0．推论：对于函数 y ＝ Asin( ωx＋ φ)或 y ＝Acos(ωx＋ φ)假设函数 y ＝ f(x)为偶函数f(0)＝ ±A ． 假设函数 y ＝ f(x)为奇函数 f(0) ＝ 0．4．求 f(x)＝ Asin( x ＋ )＋B(A ＞ 0)的解析式方法：待定系数法2π步骤：〔 1〕由周期 T ＝|ω|得 ；A ＝ y max － y min，A ＋B ＝ y max ，2〔 2〕由 － A ＋ B ＝ y min ， 得，B ＝ y max ＋ y min ，2〔 3〕将点代入求(尽量代入最高点或最低点) ．三、归类稳固*1 ．在同一平面直角坐标系中，函数 y ＝ cos(x＋3πy ＝1的交点个数22)(x? [0,2π]) 的图象和直线2是．答案： 2．〔利用三角函数图像〕解析： y cos( x3)( x [ 0，2]) ，得到y＝sinx，做出图像．222**2 ．定义在区间 [0,3π]上的函数 y=sin2x 的图象与y=cosx 的图象的交点个数是．［答案］ 7(考查三角函数图像 )．*3 ．函数 y＝ |sinx|， (x∈ [ ， 2 ]) 的单调递增区间是．答案： [ ，3π2 ]； (考查三角函数的图像和性质 )．**4 ．函数 f(x) ＝2sin (2 x＋φ)(|φ|＜π〕的局部图象如下图，那么f(0)＝ ________．答案：－ 1； (考查三角函数的图象 )．***5．将函数 f (x)2sin2x的图像向右平移(0) 个单位，再将图像上每一点横坐标缩短到原来的1 倍，所得图像关于直线x对称，那么的最小正值为．24答案：3π8 (考查三角函数图像变换 )．π π*6 ．函数 y＝ 2sin(6x－3)(0 ≤x≤ 9)的最大值与最小值之差为．答案： 2＋ 3；( 考查三角函数的最值 ) ．ππ**7 ．假设函数 f(x)＝ sin(x＋θ)(0＜θ＜2)的图象关于直线x＝6对称，那么θ＝．π答案：3； (考查三角函数的对称性)．π***8 ．假设将函数 f(x)＝sin〔 2x＋4)的图象向右平移φ个单位，所得图象关于y 轴对称，那么φ的最小正值是________．3π答案：8； (考查三角函数图象变换，三角函数的奇偶性)．π2π．*9 ．函数 f(x)＝ sinx〔≤x≤〕的值域为63答案： [1， 1]( 考查三角函数值域 )．2sin x2．**1- ．设 0＜ x＜，那么函数y的最小值为2sin x答案：5〔考查正弦函数、余弦函数的图象和性质〕．2t2解析：令t＝ sinx 〔0， 1〕，利用 y＝2＋t的单调性得到最小值．***11．将函数f(x)＝ sin2x 的图像向右平移(0)个单位后得到函数g(x)的图像，假设对满足2f ( x1)g (x2 ) 2 的x1， x2，有x1x2 min3，那么．答案：π12(考查三角函数图像变换，最值 )．π*12 ．假设 f(x)＝ 2sin ωx(0< ω<1)在区间 [0，3] 上的最大值是2，那么ω＝________．3答案：4(考查三角函数单调性 ,最值 )．ππ**13 ．将函数 f( x)＝ 2sin(2x－6)的图象向左平移m 个单位 (m＞ 0)，假设所得的图象关于直线x＝对称，那么 m6的最小值为．π答案：6； ( 考查三角函数的图象与对称性 )．***14 ．过原点的直线与函数 y＝ |sin x|(x≥ 0)的图像有且只有三个交点，α是交点中横坐标的最大值，那么2α＋αsin 22α的值为 ________．答案： 1(考查三角函数图像)．类型三：两角和与差的三角函数一、前测回忆1．sin 200cos100cos1600 sin100=．答案：1．22．sin()1,sin()1,那么 tan a=．210tan b答案：3．2解析：把两角和与差的正弦公式中的sin a cos b, cos a sin b分别看成一个整体，通过解方程组，求出sin a cos b和 cos a sin b，作比，即可求出tan a=3 .tan b23．tan230tan370 3 tan 230 tan 370．答案： 3 ．00000) =tan230+ tan37解析：因为 23+37= 60，联想公式 tan(23 + 3700 ,逆用两角和正切公式，并进行1 - tan23 tan37变形得： tan230+ tan370+3tan230 tan370 = 3．二、方法联想如何根据题目中的三角函数结构形式，选择适宜的方法来解决问题？1.分析结构：认真分析式子和所求式子的整体结构之间的异同点，帮助我们找到变形的方向；2. 寻找规律：寻求函数名之间、角之间的差异和联系为我们选用正确的方法做好前期准备；3. 巧用方法：熟练掌握解决三角求值、化简的常用方法：切化弦法、升降幂法、辅助元素法、法等，熟悉角的拆拼、变换的技巧．“ 1的〞代换三、归类稳固**1 ． (1+ tan22 0 )(1+ tan230 ) = ．答案： 2．***2 ．,那么sin 2a．tan(a + b) = 2,tan(a - b) = 3=cos2b答案： 5．7解析：观察和所求式子的特点，利用2a = (a + b )+ (a - b ),2b = (a + b ) - (a - b ) ,再利用弦化切，sin2 a tan(a +b ) + tan(a - b ) 5.求出 cos2 b = 1+ tan( + b )tan( a - b ) =7a类型四：三角恒等变换一、前测回忆1． cos(π 1π ＝π ；， cos(2 π．＋ ) ＝ ，∈ (0， )，那么 cos； sin( ＋)＝＋ )＝63236答案： 1〔 3＋ 2 2〕； 1； 1〔 2 2－ 3〕．6 3 6π 3 17π7π sin2x ＋ 2sin 2x．2．cos(＋ x)＝ ，＜ x ＜，那么1－ tanx＝4512428 答案： 75．二、方法联想1．三角变换根本想法（ 1〕角：观察角的联系，实现角的统一．（ 2〕名：弦切互化，异名化同名．形：公式变形与逆用．幂：平方降幂，根式升幂．解题前先观察角的联系，分析角的变化，实现角的统一，从而决定解题方向，再结合三角函数名、公式的变形、幂的升降，做出公式的选择．常见的角的变形有： 〔 1〕可化为特殊角； 〔 2〕可以化为同角； 〔 3〕可分析角与角之间的关系，如和，差，倍等等；〔 4〕可实现条件、结论中角的转化．注意点：判断角的范围，确定三角函数值的正负或角的值．假设在范围内不能确定时，利用三角函数值的正负或大小来缩小角的范围．三、 归类稳固2sin50 ＋°sin80 (1°＋ 3tan10 )°．**1 ．计算 1＋ cos10 ° ＝答案： 2．π 1 sin2 － cos 2．**2 ． tan( ＋ )＝ ．那么＝421＋ cos2答案：－ 5．6**3 ． sin α＝5， sin(α－β)＝－ 10， α， β均为锐角，那么角 β＝________．510π 答案：．422π**4 ．函数f(x)＝cos x ＋cos (x ＋ 3)．（ 1〕求 f(x)最小正周期和单调递增区间；π π（ 2〕求 f(x)在区间 [－ ， ]上的最大值和最小值．3 61 cos2 x解析：〔 1〕 f(x)1 cos2x31 1 cos2x cos2 x2222 31 1 cos2 x1 cos2 x 3sin 2x11cos 2x2 2226周期 T单调递增区间：2k2x25kx112k k61212所以 f x 单调递增区间：511k ,k Z ．k,1212〔 2〕x,2x, c o s x20 , 1 36622．6类型五：解三角形一、前测回忆1．〔 1〕在△ ABC 中， b＝ 3， B＝ 60°， c＝ 1，那么 C＝；a＝．答案： 30°； 2．〔 2〕在△ABC 中， A＝ 1200， a＝7， b＋ c＝8，那么 b＝；c＝．答案： 3 或 5； 5 或 3．（3〕如图，在四边形 ABCD 中， AD CD， AD ＝ 10， AB＝ 14，BDA＝ 60 ，BCD＝ 135，那么BC＝．答案： 8 2．2．〔 1〕在△ ABC 中， acosA＝ bcosB，那么△ABC 的形状为．答案：等腰或直角三角形．〔 2〕在△ABC 中， sinA＝ 2cosBsinC，那么△ ABC 的形状为．答案：等腰三角形．二、方法联想1．解三角形〔 1〕三角形的几个关系①角角关系： A＋ B＋ C＝π；②边角关系：正弦定理和余弦定理，大边对大角；③边边关系：两边之和大于第三边，两边之差小于第三边．（2〕解三角形方法①三角形的六个量中只要知道其中三个量〔至少一条边〕便可以求出其他三个量；②正弦定理运用的条件是：两角一边，两边和其中一边说对的角；余弦定理运用的有条件是：两边一夹角，三边；其中两边和其中一边说对的角的条件，既可以用正弦定理也可以用余弦定理，但都必须注意“一解〞和“两解〞的问题．2．与三角形有关的三角函数问题具体做法：（1〕 A＋B＋ C＝π可消元；（2〕遇到正弦要留神！优先考虑可能出现的一解和两解问题；b2＋ c2－ a21〕 a＝2RsinA，b＝2RsinB，c＝ 2RsinC 或〔 2〕cosA＝等进行边角互 2bc 化，即边化角或角化边．说明：在解答题中，由于考三角函数的变形较为常见，所以，常常“边化角〞，而在填空题中，随意．三、归类稳固*1 ．在△ABC 中，内角 A， B， C 的对边依次为a， b， c，假设 3a＝ 2b，那么2sin2B－ sin2A＝．sin2 A答案：7；(考查正弦定理 )．2**2 ．在△ ABC 中，角 A， B，C 的对边依次为a，b，c，假设角 A，B，C 依次成等差数列，且a＝ 1，b＝3，，那么△ ABC 的面积为．答案：23；(考查正弦定理)．***3 ．在△ ABC 中，内角 A，B，C 的对边依次为a，b，c，假设 a2－c2＝ 3b，且 sinB＝ 8cosAsinC，那么边 b＝．答案： 4；(考查两角和差的三角函数关系，正余弦定理)．1，AB ＝ 1， BC＝ 2 ，那么 AC＝．*4 ．钝角△ ABC 的面积是2答案：5； (考查正、余弦定理 )．**5 ．在△ABC 中，内角 A，B， C 所对的边分别为 a， b， c，△ ABC 的面积为 3 15， b－ c＝ 2，1，那么 a 的值为 ________．cos A＝－4答案： 8； (考查余弦定理，三角形面积 )．π1， BC 边上的高等于***6 ．在△ ABC 中， B＝43BC，那么 cos A＝ ________．答案：－ 10)．10 ( 考查解三角形，三角变换综合应用篇一、例题分析πππ例 1．设函数 f( x)＝ sin( x－ )－ 2cos2 x＋ 1．468〔 1〕求 f(x)的最小正周期；〔 2〕假设函数 y＝g(x)与 y＝ f( x)的图象关于直线x＝ 1 对称，求当 x? [0 ，4] 时 y＝ g(x)的最大值．3答案：〔 1〕 f(x)的最小正周期为8；〔 2〕最大值为3．2〖教学建议〗〔 1〕主要问题归类与方法：1．求三角函数周期问题，必须先将解析式化为y＝ A sin( ωx＋φ)＋B 或 y＝Acos(ωx＋φ)＋ B 的形式．2．求三角函数的最值(值域 )问题．因为函数 y＝ g(x)与 y＝ f(x)的图象关于直线x＝ 1 对称，所以问题可以转化为求f(x)＝Asin( ωx＋φ)在区间 [23，2] 上的最值．〔 2〕方法选择与优化建议：1．采用展开、降幂等方法“化一〞．将f(x)化为y＝Asin(ωx＋φ)形式，再使用周期公式．2．求三角函数的最值(值域 )问题．三角函数的最值既是高考中的一个重点，也是一个难点，其类型丰富，解决的方法比拟多．但是归纳起来常见的有下面三种类型：①化为只含有一个一次的三角函数y＝ Asin(ωx＋φ)＋ B 或 y＝ Acos(ωx＋φ)＋B 的形式，根据题中x 的范围求出ωx＋φ的范围，再确定 sin( ωx＋φ)或 cos(ωx＋φ)的最值 (值域 )；②借助公式将函数先化为y＝ f(sinx)型，通过换元法，即令t＝sinx，构造关于 t 的函数，并根据x 的范围确定 t 的取值范围，再求f(t)的最值 ( 值域 )；③函数表达形式中同时出现sinx＋ cosx (sinx－ cosx)与 sinxcosx 时，可以利用 (sinx＋ cosx)2＝ 1＋2sinxcosx 或 (sinx－ cosx)2＝ 1－ 2sinxcosx 的关系进行换元，即令t＝ sinx±cosx＝π2sin(x± )，转化为4关于 t 的函数，再求 f( t)的最值 (值域 )．3π例 2．函数 f(x)＝ sin( ωx＋φ)(ω＞ 0，0≤φ≤π)是R上的偶函数，其图象关于点M〔4，0〕对称，且在π区间 [0， ] 上是单调函数．2〔 1〕求φ的值；〔2〕求ω的值．π2答案： (1) φ＝2； (2)ω＝3或 2．〖教学建议〗〔 1〕主要问题归类与方法：1．三角函数图象轴对称问题．函数 f(x)＝ sin(ωx＋φ)(ω＞ 0， 0≤φ≤π)是R上的偶函数，说明f(x)的图象关于y 轴对称．2．三角函数图象中心对称问题．3π函数 f( x)＝ sin( ωx＋φ)( ω＞ 0， 0≤φ≤π)图象关于点M〔4，0〕对称．方法选择与优化建议：π1．从 f(x)为偶函数很容易得到f(0) ＝ sinφ＝±1，从而有φ＝kπ＋2(k∈ Z)．常用的结论有：①假设 y ＝ A sin(ωx＋ φ)为偶函数，那么有 π φ＝ k π(k ∈ Z )；φ＝ k π＋ (k ∈ Z )；假设为奇函数那么有 2π②假设 y ＝ A cos(ωx＋ φ)为偶函数，那么有 φ＝ k π(k ∈ Z )；假设为奇函数那么有φ＝ k π＋ 2(k ∈ Z )；③假设 y ＝ A tan(ωx＋ φ)为奇函数那么有 φ＝ k π(k ∈ Z )．这个结论要让学生理解并推理，不需要记忆．2．从 f 〔3π3πω 3πω π4 2(k ∈Z )．再结合函数的单调性〕＝ 0，可以得到cos＝ 0，于是＝ k π＋ ， ω＝ k ＋4442 3 3推导出 ω的值；3．对于 y ＝ A sin(ωx＋ φ)和 y ＝A cos(ωx＋ φ)来说，对称中心与零点相联系，对称轴与最值点联系；πy ＝ A sin( ωx＋ φ)的图象有无穷多条对称轴，可由方程 ωx＋ φ＝ k π＋ 2(k ∈ Z )解出；它还有无穷多个对称中心，它们是图象与x 轴的交点，可由 ωx＋ φ＝k π k(∈ Z )解出．4．对于 y ＝ A sin(ωx＋ φ)和 y ＝A cos(ωx＋ φ)来说，相邻两对称轴间的距离为T ，相邻两对称中心间的2距离也为 T，函数的对称轴一定经过图象的最高点或最低点．2例 3．向量 a ＝ (2sin( x ＋23 )，2)，b ＝ (2cos x ，0)( ＞ 0)，函数 f(x)＝ a ·b 的图象与直线y ＝－ 2＋ 3的相邻两个交点之间的距离为． [来源 :． Com]〔 1〕求函数 f(x)在 [0， 2 ] 上的单调递增区间；〔 2〕将函数 f(x)的图象向右平移 πy ＝ g(x)的图象．假设 y ＝ g( x)在 [0，b] 上至少含有 10 个12个单位，得到函数零点，求正数 b 的最小值．答案：〔 1〕 f(x)＝ π3，单调递增区间为 [ 5， 11 ]和 [ 17 ，23]；2cos(2x ＋ ) ＋12 1212126（ 2〕g(x)＝ 2cos2x ＋ 3，令 g(x)＝ 0，得 x ＝ k ＋5 或 x ＝k ＋ 7( k ?Z )，那么 g(x)在每个周期上有两个1212零点，所以 b 不小于第 10 个零点的横坐标即可，即，b 的最小值为 4 ＋ 75512＝12 ．【教学建议】〔 1〕主要问题归类与方法：1．求三角函数单调区间问题，先将解析式化为y＝ A sin( ωx＋φ)＋B 或 y＝Acos(ωx＋φ)＋ B 的形式，具体步骤为：①将ω化为正；②将ωx＋φ成一个整体，由三角函数的单调性求解．2．三角函数的周期与零点问题，先求出g(x)在每个周期上的零点个数，再确定区间端点的最小值．（2〕方法选择与优化建议：1．解决三角函数单调性问题时务必注意防止以下错误：①ω没有化为正数；②存在多个单调区间时错用“∪ 〞联结；③遗漏“k∈Z〞；④求解三角函数的单调区间时忘记考虑函数自身的定义域．2．首先要注意到函数的最小正周期为，确定函数在每个周期内的的零点个数，这里容易将b的最小值错求为第五个周期的终点．例4．a＝ (1，－ sinα)，b＝ (sin( α+2β)， 2)，a·b＝ 0．〔 1〕假设 sinβ＝3，β是钝角，求tanα的值；〔2〕求证：tan(α+β)＝3tanβ．5解答： a＝(1，－sinα)， b＝(sin(α+2β)，2)， a·b＝0，所以 sin( α+2β)－ 2 sinα＝ 0．（1〕－24 43；（2〕因为 sin(α+2 β)＝ 2 sinα，即 sin[( α+β)+β]＝ 2sin[( α+β)－β]得sin( α+β)cosβ+ cos (α+β)sin β＝ 2[sin( α+β)cosβ－ cos(α+β)sin β]移项得 sin(α+β)cosβ＝3 cos(α+β)sinβ，等式两边同时除以cos(α+β)cosβ得tan(α+β)＝ 3tanβ〖教学建议〗（1〕主要问题归类与方法：1．三角恒等变形主要是变角，变式，这个顺序也就决定解题的大的思路；2．变角是三角恒等变形中重要的第一步，根据问题的特征，主要是角的形式的统一．〔 2〕方法选择与优化建议：1．三角函数的求值问题与代数问题的求知一致，根据问题的特点可以直接计算，也可以间接计算〔解方程〕．2．三角恒等变形，首先应该变角，此题解题的关键，就是实现角中的形式，向未知角中的形式转化．例 5： a , b ? (0,p ),且 tan a = 2,cos b = -7 2． 10（ 1〕求 cos2a 的值；（ 2〕求 2a - b 的值．3解 〔 1〕 cos2a = -．（ 2〕 2a - b = -p．42 2 22 2cos a - sin a= 2- tan a解析： cos2a =cos a - sin a =222 ，cos a +sin a 1+tan a因为 tan a = 2,所以 cos2a = -3．5（ 2〕因为 a ? (0,p )，且 tan a = 2,所以 a ? (0, p) 2 又 cos2a = - 3，∴ 2a ? (p,p ) , sin 2a = 4， 52 57 2因为 b ? (0,p )， cos b = -．所以 sin2, b ? (p , p ) ，1022所以 sin(2a - b ) = sin2 a cos b - cos2a sin b = -2又 2a - b ? (-p , p) ， 2 2∴ 2a - b = -p． 4〖教学建议〗〔 1)主要问题归类与方法：问题 1、 cos2α＝cos 2α－ sin 2α＝2cos 2α－1＝1－2sin 2α．问题 2、由于 cos2α＝ cos 2α－sin 2 α， 这可以化为tan α的齐次式．方法选择与优化建议：对于问题 1，选择以上三个公式中的任何一个都可以，但在从α∈ (0，π)，tan α＝2 求 cos α、sin α时要注意判断它们的符号．对于问题 2，cos2α＝ cos 22cos 2α－sin 2α 1－tan 2α，处理起来更加便捷．α－ sin α＝ sin 2 α＋ cos 2α＝tan 2α＋1（ 2)主要问题归类与方法：求角的问题求角就需要选择一个关于 2α－ β的三角函数，它可以是正弦、余弦，也可以是正切，关键在于这个三角函数值可以求．另外， 2α－ β的范围不仅影响角的结果，也影响着选择正弦、余弦、正切中的哪个三角函数．方法选择与优化建议：π π通过推理，我们得到 2α－ β∈( －2， 2)，所以可以选择计算 sin(2α－β)值，也可以选择计算tan(2α－ β)的π π值，但不宜选择计算 cos(2α－β)，因为在 (－ 2，2) 上，正弦函数、正切函数都是单调的，而余弦函数却是不单调的．例 6：在 △ABC 中，内角 A ，B ， C 的对边分别为a ，b ，c ， cosA － 2cosC ＝ 2c － a ．cosBb（ 1〕求sinCsinA 的值；（ 2〕假设 cosB ＝ 1， △ ABC 的周长为 5，求 b 的大小．4答案：〔 1〕sinCsinA＝ 2；〔 2〕 b＝2．〖教学建议〗〔 1〕主要问题归类与方法：1．边角互化问题，方法有：①利用 a ＝2RsinA ， b ＝2RsinB ， c ＝ 2RsinC 将边化为角；②利用 cosA ＝ b 2＋ c 2－ a 2等将余弦化为边；2bc③ ccosB ＋ bcosC ＝ a 等化角为边．2．求边长问题，方法有：①利用正弦定理求边；②利用余弦定理求边．〔 2〕方法选择与优化建议：1．对于等式cosA － 2cosC＝2c －a的右边，我们可以选择方法①，化变为角，推导出sinC ＝ 2sinA ；cosBbb2＋ c 2－ a 2 cosA －2cosC 2c －a如果利用 cosA ＝2bc 等将等式cosB＝ b 的左边余弦化为边来做，运算量较大，所以不选择方法②．cosA － 2cosC 2c － a由于等式cosB＝b可以化为 bcosA ＋ acosB ＝ 2(bcosC ＋ccosB)，即 c ＝2a ，所以也可以选择方法③．2．因为从第一问已经可以得到c ＝ 2a ，又 a ＋ b ＋ c ＝ 5，所以三边可以转化为只含有一个未知量 b ，利用减元消元解方程的方法解决问题，因此选择方法②的余弦定理解决问题比拟方便．例 7： △ ABC 的内角 A ，B ， C 的对边依次为a ，b ，c ，假设满足 3tanAtanB － tanA － tanB ＝ 3．（ 1〕求∠ C 的大小；（ 2〕假设 c ＝ 2，且 △ ABC 为锐角三角形，求 a 2＋ b 2 的取值范围．π 〔 2〕 (20， 8)] ．答案：〔1〕 ；33〖教学建议〗〔 1)主要问题归类与方法：1．求三角形中的某个角的大小：利用三角公式求这个角的某一三角函数．2．求代数式的范围问题．利用函数的知识，转化为求函数值域．1．由于此题中涉及到的三角函数为正切，所以考虑求角的正切值，从而求角的大小；三角恒等变形中应注意公式的变形使用，解三角形问题时要注意利用隐含条件A＋ B＋ C＝．2．利用正弦定理将a2＋ b2表示为角 A 或角 B 的三角函数关系式，并将之变形整理为f(x) ＝Asin( x ＋)＋ B 的形式求范围．此题中需注意的是“△ ABC为锐角三角形〞必须保证所有的角都是锐角，这是求范围的关键所在．例 8：如图，游客从某旅游景区的景点 A 处下山至 C 处有两种路径．一种是从A 是先从 A 沿索道乘缆车到B，然后从 B 沿直线步行到C．现有甲、乙两位游客从步行，速度为50 m/min ．在甲出发 2 min 后，乙从 A 乘缆车到B，在 B 处停留沿直线步行到 C，另一种A 处下山，甲沿 AC 匀速1 min 后，再从 B 匀速步行到 C．假设缆车匀速直线运动的速度为130 m/min ，山路 AC 长为 1260 m，经测量 cos A＝1213，cos C＝35．(1)求索道 AB 的长；(2)问：乙出发多少分钟后，乙在缆车上与甲的距离最短？(3) 为使两位游客在 C 处互相等待的时间不超过 3 分钟，乙步行的速度应控制在什么范围内？答案： (1) AB 的长为 1 040 m ．；35(2)当 t＝37 min 时，甲、乙两游客距离最短．1 250， 625(3)乙步行的速度应控制在4314( 单位：m/min)范围内．〖教学建议〗〔 1)主要问题归类与方法：1．求角及边长问题，方法为先利用两角和差关系求sin B，再利用正弦定理求边长AB．2．余弦定理应用问题，其中涉及二次函数最值问题．方法为利用余弦定理和函数思想，将甲乙距离表示为乙出发后时间t 的函数．3．解三角形的实际应用问题，方法为利用正弦定理求BC，将两位游客互相等待的时间不超过 3 分钟用不等式表示，利用两者的时间差所在范围求解速度范围．1．两角一边或两边和一边对角利用正弦定理解三角形．注意点有：利用两边和一边对角求另一边的对角时容易无视解的情况的判断．2．两边和夹角，常用余弦定理求出第三边．3．求解三角形的实际问题，首先要准确理解题意，分清与所求，关注应用题中的有关专业名词、术语，如方位角、俯角等；其次根据题意画出其示意图，示意图起着关键的作用；再次将要求解的问题归结到一个或几个三角形中，通过合理运用正、余弦定理等有关知识建立数学模型，从而正确求解，演算过程要简练，计算要准确；最后作答．二、稳固练习*1 ．函数y(sin x cos x) cos x 的最小正周期为．答案：( 考查三角函数周期)．ππ*2 ．函数 f(x)＝ cos2xcos2(x－ 1)的最小正周期为．答案： 2；(考查三角函数的周期性)．**3 ．假设 tanα＝3，那么 cos2α＋ 2sin2α＝．464答案：〔三角函数正切值，求二次齐次式值〕解析：根据正切，求正余弦；或者添分母1＝ sin2α＋cos2α构造齐次分式．**4 ．θ是第三象限角，且sin θ－ 2cosθ＝－2，那么 sinθ＋cosθ＝．5答案：－3125( 构造方程组求解 sinθ， cosθ)解析：构造方程组，求解 sinθ， cosθππ*5 ．函数 f(x)＝ sin(2 x＋6)－ cos(2x＋3)的最小正周期和最大值分别为_______和 _______．答案：π； 3 (考查两角和差的正余弦公式)*6 ．函数y sin x3cos x ，且x,，那么函数的值域是_________．6答案：3, 2(考查三角函数单调性)．*7 ．函数ππf(x)＝ sin(2 x＋6)－ cos(2x＋ 3)的最小正周期和最大值分别为_______和 _______．答案：π；3〔考查两角和差的正余弦公式和三角函数的最值〕解析：展开后得到y＝ 3sin2x3π2sin2 x 的最小正周期为*8 ．函数 f(x)＝ cos(2x－4 )－ 2答案：π〔考查两角和差的余弦公式和降幂公式〕解析：展开并利用降幂公式，得到π2y＝sin〔 2x＋〕－4ππ**9 ．假设动直线 x＝ a(a∈R )与函数 f(x)＝3sin( x＋6)，g(x)＝ cos(x＋6) 的图象分别交于M， N 两点，那么MN长的最大值为．答案： 2；(考查两角和差的正余弦公式，三角函数的最值)．**10 ．假设sin α－sinβ＝－3，cos α－cos β＝1，那么 cos(α－β)的值为________．1223答案： 2 (考查两角和与差的三角函数)．sin 47 sin17 cos30**11 ．的值是；cos17答案：1(考查两角和与差的三角函数)．2**12 ．设(0, ),1sin；(0, ) ，且 tan，那么 222cos答案：(考查弦切互化)．2**13 ．在ABC 中,内角A,B,C所对的边分别是a,b,c.假设c2(a b)26,C, 那么ABC 的面积3是；答案：33(考查正 ,余弦定理 )．2π11，那么角β的大小为 ________．*14 ．α，β∈ [0，2] ，且 tan α＝ 43， cos(α＋β)＝－14答案：π3(考查角的变换 ) ．*15 ．钝角三角形ABC 的面积是1,AB1,BC 2 ,那么AC；2答案： 5 (考查正,余弦定理)．**16．在,A, B,C所对的边分别是a,b,c.又 a2, (2 b)(sin A sinB)(c b)sinC , ABC 中内角且那么ABC 的面积的最大值是；答案： 3 (考查正,余弦定理)．*17 ．ABC的内角 A, B,C 的对边分别为 a,b,c ，假设 cos A 451 ，那么 b．， cosC， a513答案：21(考查正弦定理 ,两角和与差公式 )．13**18 ．△ ABC 中， B＝ 45°， AC＝ 4，那么△ ABC 面积的最大值为 ________．答案：4＋ 42(考查余弦定理 ,根本不等式 )．**19．在△ABC中，角A，B，C所对应的边分别为a，b，c．bcos C＋ccos B＝2b，那么ab＝________．答案： 2(考查正弦定理,两角和与差公式)．**20 ．设函数 f(x)＝ Asin( ωx＋φ)(A ＞ 0,π π,且f ( )2f ( ) ,＞ 0)假设 f( x)在区间 [， ] 上具有单调性 f ( )62236那么 f(x)的最小正周期为．答案：(考查三角函数图像性质及周期性)．π***21 ．假设函数 y＝cos2x＋3sin2x＋ a 在 [0，2]上有两个不同的零点，那么实数a的取值范围为____________．答案： (－ 2，－ 1)； (考查两角和差的三角函数关系式，三角函数的零点)．22．cos 1, cos()13，且 0. 7142*〔 1〕求tan 2的值；**〔 2〕求.答案：〔1〕8 3〔2〕(考查两角和与差公式,二倍角公式 )．47323．在ABC 中，AB2, AC 3, A 60 ．*〔 1〕求BC的长；**〔 2〕求sin 2C的值． [答案：〔 1〕3(考查余弦定理 )．（2〕4 3(考查正弦定理，二倍角公式 )．724．在△ABC 中，内角A，B， C 所对的边分别为a， b， c． b+c=2a cos B．**〔 1〕证明： A=2B；**〔 2〕假设△ ABC 的面积S=a2，求角 A 的大小．4解析：〔 1〕由正弦定理得：sinB+ sinC = 2sin AcosB ,故2sin AcosB = sinB+ sin(A+ B) = sinB+sinAcosB+ cosAsinB,于是 sinB=sin(A- B)．又A, B ? (0,p ),故 0 < A - B < p,所以B = p - (A - B) 或B = A- B，因此 A = p(舍去)或A = 2B,所以， A = 2B．〔 II 〕由S a2得1ab sin C a2，故有4241sin sin C sin 2sin cos，2因 sin0 ，得 sin C cos．又， C0,，所以 C．2当C时，；22当 C时，．24综上，或．( 考查正弦定理，两角和与差公式)．2425．在△ABC 中， A、 B、C 为三个内角，2π B)＋ 3cos 2B－ 2cos B．f(B)＝ 4cos B·sin〔＋24* (1) 假设 f(B)＝ 2，求角B；* * (2) 假设 f(B)－ m＞ 2 恒成立，求实数m 的取值范围．解 (1)f( B) ＝2cos B(1＋ sin B)＋ 3cos 2B－ 2cos B＝2cos Bsin B＋ 3cos 2Bπ＝sin 2B＋ 3cos 2B＝ 2sin〔2B ＋3) ．π∵ f(B)＝ 2，∴ 2sin〔 2B＋3)＝ 2，π ππ∵ 0＜B ＜ π，∴ 2B ＋ 3＝2．∴ B ＝ 12． (考查两角和与差公式,二倍角公式 )．π(2)f(B)－ m ＞ 2 恒成立，即 2sin 〔 2B ＋3)＞ 2＋ m 恒成立．π∴ 2sin 〔 2B ＋ 3)∈ [－ 2,2] ，∴ 2＋ m ＜－ 2．∴ m ＜－ 4． (考查两角和与差公式 )．4 26． 在 △ABC 中， AC6,cosB,C．54* 〔 1〕求 AB 的长；** 〔 2〕求 cos( A - π) 的值． 6解〔 1〕因为 cosB4 ,0 B , 所以 sin B1 cos2 B1 ( 4 )23 ,55 5ACABAC sin C6 2由正弦定理知25 2.sin B，所以 ABsin B 3sinC5〔 2〕在 △ABC 中 A B C ，所以 A( B C).于是 cosAcos(B C)cos() cos B cos sin B sin ,B44 4又 cosB4,sin B3, ，故 cos A4 2 3 22555 2 5210因为 0A，所以 sin A1 cos2 A 7 210因此 cos(A) cos Acos sin Asin23 7 2 1 7 2 6 .666 10 210220(考查正弦定理，两角和与差公式)．π27． 函数f( x)＝ 4cos ωx·sin( ωx＋ 4)(ω>0) 的最小正周期为 π．π(1) 求 ω 的值；(2) 讨论 f(x)在区间 [0 ，2]上的单调性．解 (1) ω＝1．π π π (2) f(x) 在区间 [0，]上上单调递增,在区间 [ ， ] 上单调递减．88 2解析：〔 1〕 f (x) = 4cos w xsin(wx + p) = 2 2sin wxcoswx+ 2 2 cos 2 wx4= 2(sin2wx+ cos2wx) + 2= 2sin(2wx + p) + 24所以 T =2p= p , w = 1．2w(2) 由〔 1〕知： f (x) = 2sin(2 x+ p)+2 ,4因为 0 ￡x ￡p,所以 p￡2x + p5p， ￡2 4 4 4当p￡2x + p ￡p时，即 0 ￡x ￡p时， f (x)是增函数；4 4 2 8 当p￡2x + p 5p时，即 p ￡x ￡p时， f (x)是减函数； ￡ 4 2 4 8 2éùé,pù所以 f ( x) 在区间0, p上单调递增；f (x)在区间 p上单调递减ê8 úê2 ú? ??8 ?说明：考查正弦函数的图象和性质，方法为“化一 〞．28．某单位设计一个展览沙盘，现欲在沙盘平面内，布设一个对角线在为充分利用现有材料，边BC ，CD 用一根 5 米长的材料弯折而成，边折而成，要求∠ A 和∠ C 互补，且 AB ＝ BC ．l 上的四边形电气线路，如下图，BA 、AD 用一根 9 米长的材料弯(1) 设AB ＝ x 米，cos A ＝ f(x)，求f(x)的解析式，并指出x 的取值范围；(2) 求四边形 ABCD 面积的最大值．解(1) 在 △ABD2AB ·AD ·cos A ．中，由余 弦定理得BD 2 ＝ AB 2 ＋ AD 2 －同理，在 △ CBD 中， BD 2＝ CB 2＋ CD 2－ 2CB ·CD ·cos C ．因为∠ A 和∠ C 互补，所以AB 2＋ AD 2 － 2AB ·AD ·cos A ＝ CB 2＋ CD 2－ 2CB ·CD ·cos C ＝ CB 2＋ CD 2＋2CB·CD·cos A．即x2＋(9－ x)2－2x(9－ x)cos A＝ x2＋ (5－ x)2＋ 2x(5－x) ·cos A．解得 cos A＝2，即 f(x)＝2，其中 x∈(2,5) ．(考x x查角的变换 ,余弦定理 )．112(2) 四边形 ABCD的面积S＝2 (AB ·AD ＋ CB·CD )sin A ＝2[x(9 － x) ＋ x(5 － x)]1－ cos A ＝ x(7－ x)2 222221－x＝x－－ x＝x－x－14x＋．记g(x)＝ (x2－ 4)( x2－ 14x＋ 49)， x∈ (2,5)．由g′(x)＝ 2x(x2－ 14x＋ 49)＋ (x2－ 4)(2x－ 14)＝2(x－ 7)(2x2－ 7x－ 4)＝0，解得 x＝4．函数 g(x)在区间 (2,4)内单调递增，在区间(4,5)内单调递减．因此g(x)的最大值为g(4) ＝12×9＝ 108．所以 S 的最大值为108＝ 6 3． (考查角的变换,导数求最值 )．答：所求四边形ABCD 面积的最大值为 6 3 m2．π29．函数 (x) ＝2cos(2x＋3)－ cos2x＋ 1．〔 1〕求 f(x)的对称中心〔 2〕假设锐角△ ABC 中角 A,B,C 所对的边分别为a，b，c，且 f(A)＝ 0，求b的取值范围．c13解析：〔1〕 f x 2 cos2 x sin 2x cos2 x 1 223sin 2 x cos2 x 12sin 2x16对称中心为： 2x kxkZ 12k62对称中心为：k ,112南京市2018届高三数学二轮专题复习资料专题3：三角函数与解三角形〔 2〕由可得：2sin 2 A10 sin 2 A16262 A〔舍〕或 2A5A66663bsin C3cosC1sin C31 sin B322c sin C sin C sin C2tan C2因为ABC 为锐角三角形0C2C,26 0B 2C32tan C3b 1,2 (考查三角的变换,正弦定理，三角函数的性质)．3c2。

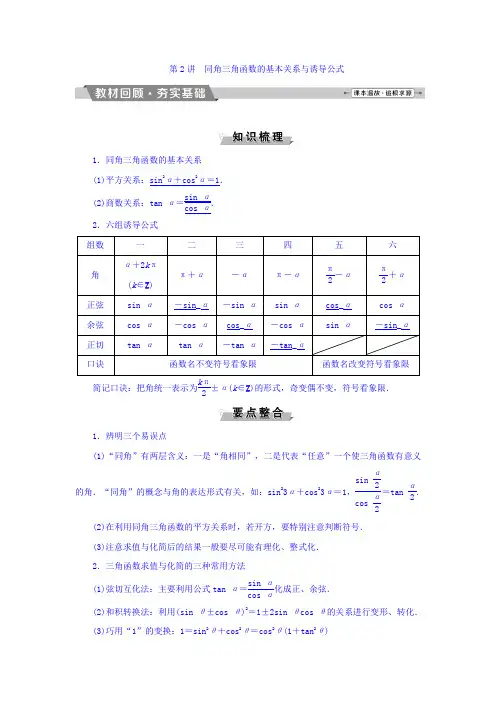
第2讲 同角三角函数的基本关系与诱导公式1．同角三角函数的基本关系 (1)平方关系：sin 2α＋cos 2α＝1． (2)商数关系：tan α＝sin αcos α．2．六组诱导公式简记口诀：把角统一表示为k π2±α(k ∈Z )的形式，奇变偶不变，符号看象限．1．辨明三个易误点(1)“同角”有两层含义：一是“角相同”，二是代表“任意”一个使三角函数有意义的角．“同角”的概念与角的表达形式有关，如：sin 23α＋cos 23α＝1，sinα2cosα2＝tan α2.(2)在利用同角三角函数的平方关系时，若开方，要特别注意判断符号． (3)注意求值与化简后的结果一般要尽可能有理化、整式化． 2．三角函数求值与化简的三种常用方法(1)弦切互化法：主要利用公式tan α＝sin αcos α化成正、余弦．(2)和积转换法：利用(sin θ±cos θ)2＝1±2sin θcos θ的关系进行变形、转化． (3)巧用“1”的变换：1＝sin 2θ＋cos 2θ＝cos 2θ(1＋tan 2θ)＝tan π4＝….1．cos ⎝ ⎛⎭⎪⎫－20π3＝( ) A.12 B.32 C ．－12D ．－32C2．已知sin ⎝ ⎛⎭⎪⎫π2＋α＝35，α∈⎝⎛⎭⎪⎫0，π2，则sin(π＋α)等于( )A.35 B ．－35C.45D ．－45D 因为sin ⎝⎛⎭⎪⎫π2＋α＝35，α∈⎝ ⎛⎭⎪⎫0，π2， 所以cos α＝35，所以sin α＝45，所以sin(π＋α)＝－sin α＝－45.3．若sin θcos θ＝12，则tan θ＋cos θsin θ的值是( )A ．－2B ．2C ．±2D.12B tan θ＋cos θsin θ＝sin θcos θ＋cos θsin θ＝1cos θsin θ＝2.4．若sin θ＝－45，tan θ>0，则cos θ＝________．由已知，θ在第三象限， 所以cos θ＝－1－sin 2θ＝－1－（－45）2＝－35.－355.教材习题改编 已知tan θ＝2，则sin θ·cos θ＝________． sin θcos θ＝sin θ·cos θsin 2θ＋cos 2θ＝tan θtan 2θ＋1＝222＋1＝25. 25同角三角函数的基本关系式(高频考点)同角三角函数的基本关系式的应用很广泛，也比较灵活．高考中常以选择题、填空题的形式出现．高考对同角三角函数基本关系式的考查主要有以下三个命题角度： (1)知弦求弦； (2)知弦求切； (3)知切求弦．(1)(2016·高考全国卷丙)若tan α＝34，则cos 2α＋2sin 2α＝( )A.6425 B.4825C ．1D.1625(2)已知sin α＋2cos α＝3，则tan α＝( ) A.22 B. 2 C ．－22D ．－ 2【解析】 (1)法一：由tan α＝sin αcos α＝34，cos 2α＋sin 2α＝1，得⎩⎪⎨⎪⎧sin α＝35，cos α＝45或⎩⎪⎨⎪⎧sin α＝－35，cos α＝－45，则sin 2α＝2sin αcos α＝2425，则cos 2α＋2sin 2α＝1625＋4825＝6425. 法二：cos 2α＋2sin 2α＝cos 2α＋4sin αcos αcos 2α＋sin 2α＝1＋4tan α1＋tan 2α＝1＋31＋916＝6425. (2)因为sin α＋2cos α＝3， 所以(sin α＋2cos α)2＝3，所以sin 2α＋22sin αcos α＋2cos 2α＝3， 所以sin 2α＋22sin αcos α＋2cos 2αsin 2α＋cos 2α＝3，所以tan 2α＋22tan α＋2tan 2α＋1＝3， 所以2tan 2α－22tan α＋1＝0，所以tan α＝22. 【答案】 (1)A (2)A同角三角函数关系式及变形公式的应用(1)利用sin 2α＋cos 2α＝1可以实现角α的正弦、余弦的互化，利用sin αcos α＝tan α可以实现角α的弦切互化．(2)应用公式时注意方程思想的应用：对于sin α＋cos α，sin αcos α，sin α－cos α这三个式子，利用(sin α±cos α)2＝1±2sin αcos α，可以知一求二．角度一 知弦求弦1．(2017·雅安模拟)已知sin θ＋cos θ＝43，θ∈(0，π4)，则sin θ－cos θ的值为( )A.23 B.13 C ．－23D ．－13C (sin θ＋cos θ)2＝169，所以1＋2sin θcos θ＝169，所以2sin θcos θ＝79，由(sin θ－cos θ)2＝1－2sin θ·cos θ＝1－79＝29，可得sin θ－cos θ＝±23.又因为θ∈(0，π4)，sin θ<cos θ，所以sin θ－cos θ＝－23.角度二 知弦求切2．已知cos ⎝ ⎛⎭⎪⎫π2＋α＝35，且α∈⎝ ⎛⎭⎪⎫π2，3π2，则tan α＝( )A.43 B.34 C ．－34D ．±34B 因为cos ⎝⎛⎭⎪⎫π2＋α＝35，所以sin α＝－35，显然α在第三象限，所以cos α＝－45，故tan α＝34.角度三 知切求弦3．若sin α＝2sin β，tan α＝3tan β，则cos α＝________． 因为sin α＝2sin β，① tan α＝3tan β， tan 2α＝9tan 2β.②由①2÷②得：9cos 2α＝4cos 2β.③ 由①2＋③得sin 2α＋9cos 2α＝4. 又sin 2α＋cos 2α＝1， 所以cos 2α＝38，所以cos α＝±64. ±64诱导公式的应用(1)sin(－1 200°)cos 1 290°＋cos(－1 020°)·sin(－1 050°)＝________．(2)已知cos α是方程3x 2－x －2＝0的根，且α是第三象限角，则sin （－α＋3π2）cos （3π2＋α）tan 2（π－α）cos （π2＋α）sin （π2－α）等于________．(3)已知cos(π6－α)＝23，则sin(α－2π3)＝________．【解析】 (1)原式＝－sin 1 200°cos 1 290°－cos 1 020°·sin 1 050°＝－sin(3×360°＋120°)cos(3×360°＋210°)－cos(2×360°＋300°)sin(2×360°＋330°)＝－sin 120°cos 210°－cos 300°sin 330°＝－sin(180°－60°)cos(180°＋30°)－cos(360°－60°)·sin(360°－30°) ＝sin 60°cos 30°＋cos 60°sin 30° ＝32×32＋12×12＝1. (2)因为方程3x 2－x －2＝0的根为x 1＝1，x 2＝－23，由题知cos α＝－23，所以sin α＝－53，tan α＝52. 所以原式＝－cos αsin αtan 2α－sin αcos α＝tan 2α＝54.(3)因为⎝ ⎛⎭⎪⎫π6－α＋⎝ ⎛⎭⎪⎫α－2π3＝－π2，所以α－2π3＝－π2－⎝ ⎛⎭⎪⎫π6－α，所以sin ⎝ ⎛⎭⎪⎫α－2π3＝sin ⎣⎢⎡⎦⎥⎤－π2－⎝ ⎛⎭⎪⎫π6－α＝－cos ⎝ ⎛⎭⎪⎫π6－α＝－23.【答案】 (1)1 (2)54 (3)－23(1)诱导公式用法的一般思路 ①化大角为小角．②角中含有加减π2的整数倍时，用公式去掉π2的整数倍．(2)常见的互余和互补的角①常见的互余的角：π3－α与π6＋α；π3＋α与π6－α；π4＋α与π4－α等．②常见的互补的角：π3＋θ与2π3－θ；π4＋θ与3π4－θ等．(3)三角函数式化简的方向 ①切化弦，统一名． ②用诱导公式，统一角．③用因式分解将式子变形，化为最简．1．(2017·福建省毕业班质量检测)若sin(π2＋α)＝－35，且α∈(π2，π)，则sin(π－2α)＝( )A.2425 B.1225C ．－1225D ．－2425D 由sin(π2＋α)＝cos α＝－35，且α∈(π2，π)，得sin α＝45，所以sin(π－2α)＝sin 2α＝2sin αcos α＝－2425，选项D 正确．2．sin(－1 071°)si n 99°＋sin(－171°)sin(－261°)＝________． 原式＝(－sin 1 071°)·sin 99°＋sin 171°·sin 261°＝－sin (3×360°－9°)sin(90°＋9°)＋sin(180°－9°)·sin(270°－9°)＝sin 9°cos 9°－sin 9°cos 9°＝0.故填0.3．已知cos(π＋α)＝－12，求sin[α＋（2n ＋1）π]＋sin （π＋α）sin （π－α）·cos （α＋2n π）(n ∈Z )．因为cos(π＋α)＝－12，所以－cos α＝－12，cos α＝12.sin[α＋（2n ＋1）π]＋sin （π＋α）sin （π－α）cos （α＋2n π）＝sin （α＋2n π＋π）－sin αsin αcos α＝sin （π＋α）－sin αsin αcos α＝－2sin αsin αcos α＝－2cos α＝－4.——方程思想求解三角函数值已知sin θ＋cos θ＝713，θ∈(0，π)，则tan θ＝________．【解析】 法一：因为sin θ＋cos θ＝713，θ∈(0，π)，所以(sin θ＋cos θ)2＝1＋2sin θcos θ＝49169，所以sin θcos θ＝－60169.由根与系数的关系，知sin θ，cos θ是方程x 2－713x －60169＝0的两根，所以x 1＝1213，x 2＝－513.又sin θcos θ＝－60169<0，所以sin θ>0，cos θ<0.所以sin θ＝1213，cos θ＝－513.所以tan θ＝sin θcos θ＝－125.法二：同法一，得sin θcos θ＝－60169，所以sin θcos θsin 2θ＋cos 2θ＝－60169. 齐次化切，得tan θtan 2 θ＋1＝－60169，即60tan 2θ＋169tan θ＋60＝0， 解得tan θ＝－125或tan θ＝－512.又θ∈(0，π)，sin θ＋cos θ＝713>0，sin θcos θ＝－60169<0.所以θ∈(π2，3π4)，所以tan θ＝－125.【答案】 －125(1)本题利用方程思想法一：由sin θ＋cos θ、sin θcos θ的值构造一元二次方程，把sin θ与cos θ看作此方程的两根，即可求出sin θ与cos θ的值，便可求解．法二：利用三角函数的基本关系转化为关于tan θ的一元二次方程求解．(2)所谓方程思想就是在解决问题时，用事先设定的未知数沟通问题中所涉及的各量间的等量关系，建立方程或方程组，求出未知数及各量的值，或者用方程的性质去分析、转化问题，使问题获得解决．已知sin(3π－α)＝－2sin(π2＋α)，则sin αcos α等于( )A ．－25 B.25C.25或－25D ．－15A 因为sin(3π－α)＝sin(π－α)＝－2sin(π2＋α)，所以sin α＝－2cos α，所以tan α＝－2，当α在第二象限时，⎩⎪⎨⎪⎧sin α＝255cos α＝－55，所以sin αcos α＝－25；当α在第四象限时，⎩⎪⎨⎪⎧sin α＝－255cos α＝55，所以sin αcos α＝－25，综上，sin αcosα＝－25，故选A.1．tan(－233π)的值为( )A. 3 B ．－ 3 C.33D ．－33A A tan(－233π)＝tan(－8π＋π3)＝tan π3＝ 3.2．已知sin(π＋θ)＝－3cos(2π－θ)，|θ|<π2，则θ等于( )A ．－π6B ．－π3C.π6D.π3D 因为sin(π＋θ)＝－3cos(2π－θ)， 所以－sin θ＝－3cos θ，所以tan θ＝ 3. 因为|θ|<π2，所以θ＝π3.3．(2017·福建省毕业班质量检测)已知cos(α＋π2)＝13，则cos 2α的值等于( )A.79 B ．－79C.89D ．－89A 法一：因为cos(α＋π2)＝13，所以sin α＝－13，所以cos α＝±223，所以cos 2α＝cos 2α－sin 2α＝(±223)2－(－13)2＝79，故选A.法二：因为cos(α＋π2)＝13，所以sin α＝－13，所以cos 2α＝1－2sin 2α＝1－2×19＝79，故选A.4．已知sin α＋3cos α3cos α－sin α＝5，则sin 2α－sin αcos α的值为( )A ．－15B ．－25C.15D.25D 依题意得tan α＋33－tan α＝5，所以tan α＝2.所以sin 2α－sin αcos α＝sin 2α－sin αcos αsin 2α＋cos 2α＝tan 2α－tan αtan 2α＋1＝22－222＋1＝25. 5．已知f (x )＝a sin(πx ＋α)＋b cos(πx ＋β)＋4，若f (2 016)＝5，则f (2 017)的值是( )A ．2B ．3C ．4D ．5B 因为f (2 016)＝5.所以a sin(2 016π＋α)＋b cos(2 016π＋β)＋4＝5， 即a sin α＋b cos β＝1.所以f (2 017)＝a sin(2 017π＋α)＋b cos(2 017π＋β)＋4＝－a sin α－b cos β＋4＝－1＋4＝3.6．已知sin α＋3cos α＋1＝0，则tan α的值为( ) A.43或34 B ．－34或－43C.34或－43D ．－43或不存在D 由sin α＝－3cos α－1，可得(－3cos α－1)2＋cos 2α＝1，即5cos 2α＋3cos α＝0，解得cos α＝－35或cos α＝0，当cos α＝0时，tan α的值不存在，当cos α＝－35时，sin α＝－3cos α－1＝45，tan α＝sin αcos α＝－43，故选D.7．化简sin （π2＋α）cos （π2－α）cos （π＋α）＋sin （π－α）cos （π2＋α）sin （π＋α）＝________． 原式＝cos αsin α－cos α＋sin α（－sin α）－sin α＝－sin α＋sin α＝0. 08．在△ABC 中，若tan A ＝23，则sin A ＝________． 因为tan A ＝23>0，所以A 为锐角，于是1＋tan 2A ＝1＋29＝119＝1cos 2A ，cos 2A ＝911，cos A ＝31111，sin A ＝tan A cos A ＝2211. 2211 9．sin 43π·cos 56π·tan(－43π)的值是________． 原式＝sin(π＋π3)·cos(π－π6)·tan(－π－π3) ＝(－sin π3)·(－cos π6)·(－tan π3) ＝(－32)×(－32)×(－3)＝－334. －33410．已知sin ⎝ ⎛⎭⎪⎫7π12＋α＝23，则cos ⎝⎛⎭⎪⎫α－11π12＝________． cos ⎝ ⎛⎭⎪⎫α－11π12＝cos ⎝ ⎛⎭⎪⎫11π12－α ＝cos ⎣⎢⎡⎦⎥⎤π－⎝ ⎛⎭⎪⎫π12＋α＝－cos ⎝ ⎛⎭⎪⎫π12＋α， 而sin ⎝ ⎛⎭⎪⎫7π12＋α＝sin ⎣⎢⎡⎦⎥⎤π2＋⎝ ⎛⎭⎪⎫π12＋α ＝cos ⎝ ⎛⎭⎪⎫π12＋α＝23， 所以cos ⎝⎛⎭⎪⎫α－11π12＝－23. －2311．已知sin θ＝45，π2<θ<π. (1)求tan θ的值；(2)求sin 2θ＋2sin θcos θ3sin 2θ＋cos 2θ的值．(1)因为sin 2θ＋cos 2θ＝1，所以cos 2θ＝925.又π2<θ<π，所以cos θ＝－35.所以tan θ＝sin θcos θ＝－43.(2)由(1)知，sin 2θ＋2sin θcos θ3sin 2θ＋cos 2 θ＝tan 2θ＋2tan θ3tan 2θ＋1＝－857.12．已知α为第三象限角，f (α)＝sin （α－π2）·cos （3π2＋α）·tan （π－α）tan （－α－π）·sin （－α－π）.(1)化简f (α)；(2)若cos(α－3π2)＝15，求f (α)的值．(1)f (α)＝sin （α－π2）·cos （3π2＋α）·tan （π－α）tan （－α－π）·sin （－α－π）＝（－cos α）·sin α·（－tan α）（－tan α）· sin α＝－cos α.(2)因为cos(α－3π2)＝15，所以－sin α＝15，从而sin α＝－15.又α为第三象限角，所以cos α＝－1－sin 2α＝－265，所以f (α)＝－cos α＝265.13．已知sin αcos α＝18，且5π4<α<3π2，则cos α－sin α的值为() A ．－32 B.32C ．－34 D.34B 因为5π4<α<3π2，所以cos α<0，sin α<0且|cos α|<|sin α|，所以cos α－sin α>0.又(cos α－sin α)2＝1－2sin αcos α＝1－2×18＝34， 所以cos α－sin α＝32. 14．化简1－2sin 40°cos 40°cos 40°－1－sin 250°＝________． 原式＝sin 240°＋cos 240°－2sin 40°cos 40°cos 40°－cos 50°＝|sin 40°－cos 40°|sin 50°－sin 40° ＝|sin 40°－sin 50°|sin 50°－sin 40° ＝sin 50°－sin 40°si n 50°－sin 40° ＝1.115．已知在△ABC 中，sin A ＋cos A ＝15. (1)求sin A cos A 的值；(2)判断△ABC 是锐角三角形还是钝角三角形；(3)求tan A 的值．(1)因为sin A ＋cos A ＝15，① 所以两边平方得1＋2sin A cos A ＝125， 所以sin A cos A ＝－1225. (2)由sin A cos A ＝－1225<0，且0<A <π， 可知cos A <0，所以A 为钝角，所以△ABC 是钝角三角形．(3)因为(sin A －cos A )2＝1－2sin A cos A ＝1＋2425＝4925， 又sin A >0，cos A <0，所以sin A －cos A >0，所以sin A －cos A ＝75，② 所以由①，②可得sin A ＝45，cos A ＝－35，所以tan A ＝sin A cos A ＝45－35＝－43. 16．已知f (x )＝cos 2（n π＋x ）·sin 2（n π－x ）cos 2[（2n ＋1）π－x ](n ∈Z )． (1)化简f (x )的表达式； (2)求f ⎝ ⎛⎭⎪⎫π2 016＋f ⎝ ⎛⎭⎪⎫1 007π2 016的值． (1)当n 为偶数，即n ＝2k (k ∈Z )时，f (x )＝cos 2（2k π＋x ）·sin 2（2k π－x ）cos 2[（2×2k ＋1）π－x ]＝cos 2x ·sin 2（－x ）cos 2（π－x ）＝cos 2x ·（－sin x ）2（－cos x ）2 ＝sin 2x (n ＝2k ，k ∈Z )；当n 为奇数，即n ＝2k ＋1(k ∈Z )时，f (x )＝cos 2[（2k ＋1）π＋x ]·sin 2[（2k ＋1）π－x ]cos 2{[2×（2k ＋1）＋1]π－x }＝cos 2[2k π＋（π＋x ）]·sin 2[2k π＋（π－x ）]cos 2[2×（2k ＋1）π＋（π－x ）]＝cos 2（π＋x ）·sin 2（π－x ）cos 2（π－x ）＝（－cos x ）2sin 2x （－cos x ）2 ＝sin 2x (n ＝2k ＋1，k ∈Z )．综上得f (x )＝sin 2x . (2)由(1)得f ⎝ ⎛⎭⎪⎫π2 016＋f ⎝ ⎛⎭⎪⎫1 007π2 016 ＝sin2π2 016＋sin 21 007π2 016 ＝sin2π2 016＋sin 2⎝ ⎛⎭⎪⎫π2－π2 016 ＝sin2π2 016＋cos 2π2 016＝1.。

第5讲 简单的三角恒等变换 第1课时 两角和、差及倍角公式1.两角和与差的正弦、余弦、正切公式(1)C (α∓β)：cos(α∓β)＝□01cos αcos β±sin αsin β. (2)S (α±β)：sin(α±β)＝□02sin αcos β±cos αsin β. (3)T (α±β)：tan(α±β)＝□03tan α±tan β1∓tan αtan β⎝ ⎛⎭⎪⎫α，β，α±β≠π2＋k π，k ∈Z . 2.二倍角的正弦、余弦、正切公式 (1)S 2α：sin2α＝□012sin αcos α. (2)C 2α：cos2α＝□02cos 2α－sin 2α＝□032cos 2α－1＝□041－2sin 2α. (3)T 2α：tan2α＝□052tan α1－tan 2α⎝ ⎛⎭⎪⎫α≠±π4＋k π，且α≠k π＋π2，k ∈Z . 3.公式的常用变形(1)tan α±tan β＝□01tan(α±β)(1∓tan αtan β)． (2)cos 2α＝□021＋cos2α2， sin 2α＝□031－cos2α2. (3)1±sin2α＝(sin α±cos α)2， sin α±cos α＝2sin ⎝⎛⎭⎪⎫α±π4.(4)a sin α＋b cos α其中cos φ＝a a 2＋b2，sin φ＝b a 2＋b 2，tan φ＝ba(a ≠0)．1.概念辨析(1)公式C (α±β)，S (α±β)，S 2α，C 2α中的角α，β是任意的．( ) (2)存在实数α，β，使等式sin(α＋β)＝sin α＋sin β成立．( ) (3)在锐角△ABC 中，sin A sin B 和cos A cos B 大小关系不确定．( )(4)公式tan(α＋β)＝tan α＋tan β1－tan αtan β可以变形为tan α＋tan β＝tan(α＋β)(1－tan αtan β)，且对任意角α，β都成立．( )(5)对任意角α都有1＋sin α3＝⎝ ⎛⎭⎪⎫sin α6＋cos α62.( )答案 (1)√ (2)√ (3)× (4)× (5)√ 2.小题热身(1)若cos α＝－45，α是第三象限的角，则sin ⎝ ⎛⎭⎪⎫α＋π4＝( )A.－210 B.210 C ．－7210 D.7210答案 C解析 因为cos α＝－45，α是第三象限的角，所以sin α＝－1－cos 2α＝－35，所以sin ⎝ ⎛⎭⎪⎫α＋π4＝sin αcos π4＋cos αsin π4 ＝⎝ ⎛⎭⎪⎫－35×22＋⎝ ⎛⎭⎪⎫－45×22＝－7210.(2)计算：cos(α＋β)cos β＋sin(α＋β)sin β＝( ) A.sin(α＋2β) B ．sin α C.cos(α＋2β) D ．cos α答案 D解析 cos(α＋β)cos β＋sin(α＋β)sin β＝cos[(α＋β)－β]＝cos α. (3)已知cos x ＝34，则cos2x ＝( )A.－14B.14 C ．－18 D.18答案 D解析 cos2x ＝2cos 2x －1＝2×⎝ ⎛⎭⎪⎫342－1＝18.(4)在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称．若tan α＝35，则tan(α－β)的值为( )A.0B.3034C.916D.158答案 D解析 由角α与角β的始边相同，终边关于y 轴对称可知tan α＝－tan β.又tan α＝35，所以tan β＝－35， 所以tan(α－β)＝tan α－tan β1＋tan αtan β＝35－⎝ ⎛⎭⎪⎫－351＋35×⎝ ⎛⎭⎪⎫－35＝158，故选D.题型 一 两角和、差及倍角公式的直接应用1.已知角α与角β均以x 轴的非负半轴为始边，它们的终边关于y 轴对称，且角α的终边与单位圆交于点P ⎝⎛⎭⎪⎫223，13，则sin(α－β)＝________. 答案 －429解析 因为角α的终边与单位圆交于点P ⎝ ⎛⎭⎪⎫223，13， 所以sin α＝13，cos α＝223.因为角α与角β的终边关于y 轴对称，所以角β的终边与单位圆交于点Q ⎝ ⎛⎭⎪⎫－223，13，所以sin β＝13，cos β＝－223，所以sin(α－β)＝sin αcos β－cos αsin β＝13×⎝ ⎛⎭⎪⎫－223－223×13＝－429. 2.(2018·全国卷Ⅱ)已知tan ⎝ ⎛⎭⎪⎫α－5π4＝15，则tan α＝________.答案 32解析 tan ⎝⎛⎭⎪⎫α－5π4＝tan α－tan5π41＋tan α·tan5π4＝tan α－11＋tan α＝15，解方程得tan α＝32.3.已知α∈⎝ ⎛⎭⎪⎫π2，π，sin α＝55，则cos ⎝ ⎛⎭⎪⎫5π6－2α的值为________． 答案 －4＋3310解析 因为α∈⎝ ⎛⎭⎪⎫π2，π，sin α＝55. 所以cos α＝－1－sin 2α＝－255.所以sin2α＝2sin αcos α＝－45，cos2α＝cos 2α－sin 2α＝35，所以cos ⎝ ⎛⎭⎪⎫5π6－2α＝cos 5π6cos2α＋sin 5π6sin2α＝－32×35＋12×⎝ ⎛⎭⎪⎫－45＝－4＋3310.应用三角公式化简求值的策略(1)使用两角和、差及倍角公式，首先要记住公式的结构特征和符号变化规律．例如两角差的余弦公式可简记为：“同名相乘，符号反”．(2)使用公式求值，应注意与同角三角函数基本关系、诱导公式的综合应用． (3)使用公式求值，应注意配方法、因式分解和整体代换思想的应用.1.(2018·石家庄质检)若sin(π－α)＝13，且π2≤α≤π，则sin2α的值为( )A.－429 B ．－229 C.229 D.429答案 A解析 ∵sin(π－α)＝13，∴sin α＝13，又∵π2≤α≤π，∴cos α＝－1－sin 2α＝－223，∴sin2α＝2sin αcos α＝2×13×⎝ ⎛⎭⎪⎫－223＝－429. 2.(2018·上饶三模)由射线y ＝43x (x ≥0)按逆时针方向旋转到射线y ＝－512x (x ≤0)的位置所成的角为θ，则cos θ＝( )A.－1665 B ．±1665 C ．－5665 D ．±5665答案 A解析 设y ＝43x (x ≥0)的倾斜角为α，则sin α＝45，cos α＝35，射线y ＝－512x (x ≤0)的倾斜角为β，sin β＝513，cos β＝－1213，∴cos θ＝cos(β－α)＝cos αcos β＋sin αsin β＝35×⎝ ⎛⎭⎪⎫－1213＋45×513＝－1665.3.若sin(α＋β)＝12，sin(α－β)＝13，则tan αtan β等于( )A.5 B ．－1 C ．6 D.16答案 A解析 由题意可得sin αcos β＋cos αsin β＝12，sin αcos β－cos αsin β＝13，解得sin αcos β＝512，cos αsin β＝112，∴tan αtan β＝5.题型 二 两角和、差及倍角公式的逆用和变形用1.计算－sin133°cos197°－cos47°cos73°的结果为( ) A.12 B.33 C.22 D.32 答案 A解析 －sin133°cos197°－cos47°cos73° ＝－sin47°(－cos17°)－cos47°sin17° ＝sin(47°－17°)＝sin30°＝12.2.(1＋tan18°)(1＋tan27°)的值是( ) A. 3 B ．1＋ 2C.2 D ．2(tan18°＋tan27°)答案 C解析 (1＋tan18°)(1＋tan27°)＝1＋tan18°＋tan27°＋tan18°tan27°＝1＋tan45°(1－tan18°tan27°)＋tan18°tan27°＝2. 3.已知sin α＋cos α＝52，则cos4α＝________. 答案 78解析 由sin α＋cos α＝52，得sin 2α＋cos 2α＋2sin αcos α＝1＋sin2α＝54，所以sin2α＝14，从而cos4α＝1－2sin 22α＝1－2×⎝ ⎛⎭⎪⎫142＝78.条件探究1 将举例说明3的条件改为“sin α－cos α＝43”，求cos4α.解 因为sin α－cos α＝43，所以1－2sin αcos α＝169，所以sin2α＝2sin αcos α＝－79，所以cos4α＝1－2sin 22α＝1－2×⎝ ⎛⎭⎪⎫－792＝－1781.条件探究2 将举例说明3的条件改为“cos 2⎝ ⎛⎭⎪⎫α－π4＝23，α∈(π，2π)”，求sin α＋cos α.解 因为cos 2⎝ ⎛⎭⎪⎫α－π4＝1＋cos ⎝ ⎛⎭⎪⎫2α－π22＝1＋sin2α2＝23.所以sin2α＝13>0，又因为α∈(π，2π)，所以α∈⎝ ⎛⎭⎪⎫π，3π2，所以sin α＋cos α<0，(sin α＋cos α)2＝1＋2sin αcos α＝1＋13＝43，所以sin α＋cos α＝－233.1.注意三角函数公式逆用和变形用的两个问题(1)公式逆用时一定要注意公式成立的条件和角之间的关系．(2)注意特殊角的应用，当式子中出现12，1，32，3等这些数值时，一定要考虑引入特殊角，把“值变角”构造适合公式的形式．2．熟记三角函数公式的两类变式 (1)和差角公式变形sin αsin β＋cos(α＋β)＝cos αcos β， cos αsin β＋sin(α－β)＝sin αcos β， tan α±tan β＝tan(α±β)·(1∓tan αtan β)． (2)倍角公式变形降幂公式cos 2α＝1＋cos2α2，sin 2α＝1－cos2α2，配方变形：1±sin α＝⎝ ⎛⎭⎪⎫sin α2±cos α22,1＋cos α＝2cos 2α2，1－cos α＝2sin 2α2.1.若x ∈[0，π]，sin x 3sin 2x 3＝cos x 3cos 2x3，则x 的值是( )A.π6 B.π4 C.π3 D.π2答案 D解析 由已知得，cos x 3cos 2x 3－sin x 3sin 2x 3＝cos x ＝0.∵x ∈[0，π]，∴x ＝π2.2.(2019·湖南郴州质检)已知x ∈(0，π)， sin ⎝ ⎛⎭⎪⎫π3－x ＝cos 2⎝ ⎛⎭⎪⎫x 2＋π4，则tan x ＝( )A.12 B ．－2 C.22 D. 2 答案 D解析 因为sin ⎝ ⎛⎭⎪⎫π3－x ＝cos 2⎝ ⎛⎭⎪⎫x 2＋π4，所以32cos x －12sin x ＝1＋cos ⎝⎛⎭⎪⎫x ＋π22，3cos x －sin x ＝1－sin x ，解得cos x ＝33， 因为x ∈(0，π)，所以sin x ＝1－cos 2x ＝63，所以tan x ＝sin xcos x ＝6333＝ 2.3.化简：－α1－tan 2－α·sin αcos αcos 2α－sin 2α＝________. 答案 12解析 原式＝tan(90°－2α)·12sin2αcos2α＝－2α－2α·12sin2αcos2α＝cos2αsin2α·12sin2αcos2α＝12. 题型 三 两角和、差及倍角公式的灵活应用角度1 角的变换1.(2018·南开区模拟)已知0<α＜π2<β<π，cos ⎝ ⎛⎭⎪⎫β－π4＝13，sin(α＋β)＝45.(1)求sin2β的值； (2)求cos ⎝ ⎛⎭⎪⎫α＋π4的值．解 (1)sin2β＝cos ⎝⎛⎭⎪⎫π2－2β＝2cos 2⎝ ⎛⎭⎪⎫β－π4－1＝－79.(2)因为0<α<π2<β<π，所以π2<α＋β<3π2，所以sin ⎝ ⎛⎭⎪⎫β－π4>0，cos(α＋β)<0， 因为cos ⎝ ⎛⎭⎪⎫β－π4＝13，sin(α＋β)＝45， 所以sin ⎝ ⎛⎭⎪⎫β－π4＝223，cos(α＋β)＝－35， 所以cos ⎝ ⎛⎭⎪⎫α＋π4＝cos ⎣⎢⎡⎦⎥⎤α＋β－⎝ ⎛⎭⎪⎫β－π4＝cos(α＋β)·cos ⎝⎛⎭⎪⎫β－π4＋sin(α＋β)sin ⎝⎛⎭⎪⎫β－π4＝⎝ ⎛⎭⎪⎫－35×13＋45×223＝82－315.角度2 函数名称的变换2.求值：(1)sin10°1－3tan10°＝________；(2)1＋cos20°2sin20°－sin10°⎝ ⎛⎭⎪⎫1tan5°－tan5°＝________.答案 (1)14 (2)32解析 (1)sin10°1－3tan10°＝sin10°cos10°cos10°－3sin10°＝2sin10°cos10°4⎝ ⎛⎭⎪⎫12cos10°－32sin10°＝sin20°－＝14. (2)原式＝2cos 210°2×2sin10°cos10°－sin10°·⎝ ⎛⎭⎪⎫cos5°sin5°－sin5°cos5°＝cos10°2sin10°－sin10°·cos 25°－sin 25°sin5°cos5° ＝cos10°2sin10°－sin10°·cos10°12sin10° ＝cos10°2sin10°－2cos10°＝cos10°－2sin20°2sin10°＝cos10°－－2sin10°＝cos10°－2⎝ ⎛⎭⎪⎫12cos10°－32sin10°2sin10°＝3sin10°2sin10°＝32.三角公式应用中变“角”与变“名”问题的解题思路(1)角的变换：明确各个角之间的关系(包括非特殊角与特殊角、已知角与未知角)，熟悉角的变换技巧，及半角与倍角的相互转化，如：2α＝(α＋β)＋(α－β)，α＝(α＋β)－β＝(α－β)＋β，40°＝60°－20°，⎝⎛⎭⎪⎫π4＋α＋⎝ ⎛⎭⎪⎫π4－α＝π2，α2＝2×α4等．(2)名的变换：明确各个三角函数名称之间的联系，常常用到同角关系、诱导公式，把正弦、余弦化为正切，或者把正切化为正弦、余弦.1.若0<α<π2，－π2<β<0，cos ⎝ ⎛⎭⎪⎫π4＋α＝13，cos ⎝ ⎛⎭⎪⎫π4－β2＝33，则cos ⎝ ⎛⎭⎪⎫α＋β2等于( )A.33 B ．－33 C.539 D ．－69答案 C解析 ∵0<α<π2，∴π4<α＋π4<3π4.∵cos ⎝⎛⎭⎪⎫π4＋α＝13，∴sin ⎝ ⎛⎭⎪⎫π4＋α＝223.∵－π2<β<0，∴π4<π4－β2<π2.∵cos ⎝⎛⎭⎪⎫π4－β2＝33，∴sin ⎝ ⎛⎭⎪⎫π4－β2＝63.∴cos ⎝ ⎛⎭⎪⎫α＋β2＝cos ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫π4＋α－⎝ ⎛⎭⎪⎫π4－β2＝cos ⎝⎛⎭⎪⎫π4＋αcos ⎝ ⎛⎭⎪⎫π4－β2＋sin ⎝ ⎛⎭⎪⎫π4＋αsin ⎝ ⎛⎭⎪⎫π4－β2＝13×33＋223×63＝539. 2.(2018·吉林第三次调研)若sin ⎝ ⎛⎭⎪⎫π6－α＝13，则cos 2⎝ ⎛⎭⎪⎫π6＋α2＝________.答案 23解析 因为sin ⎝ ⎛⎭⎪⎫π6－α＝sin ⎣⎢⎡⎦⎥⎤π2－⎝ ⎛⎭⎪⎫π3＋α＝cos ⎝ ⎛⎭⎪⎫π3＋α＝13，所以cos 2⎝ ⎛⎭⎪⎫π6＋α2＝1＋cos ⎝ ⎛⎭⎪⎫π3＋α2＝1＋132＝23.3.(2018·江苏高考)已知α，β为锐角，tan α＝43，cos(α＋β)＝－55.(1)求cos2α的值； (2)求tan(α－β)的值．解 (1)因为tan α＝43，tan α＝sin αcos α，所以sin α＝43cos α.因为sin 2α＋cos 2α＝1，所以cos 2α＝925，因此，cos2α＝2cos 2α－1＝－725.(2)因为α，β为锐角，所以α＋β∈(0，π)． 又因为cos(α＋β)＝－55， 所以sin(α＋β)＝1－cos 2α＋β＝255，因此tan(α＋β)＝－2.因为tan α＝43，所以tan2α＝2tan α1－tan 2α＝－247， 因此，tan(α－β)＝tan[2α－(α＋β)] ＝tan2α－α＋β1＋tan2αα＋β＝－211.思想方法 三角恒等变换中的拆角、凑角思想[典例1] (2018·石嘴山一模)已知α满足sin α＝12，那么sin ⎝ ⎛⎭⎪⎫π4＋αsin ⎝ ⎛⎭⎪⎫π4－α的值为( )A ．－12 B.12 C ．－14 D.14答案 D解析 ∵sin ⎝ ⎛⎭⎪⎫π4－α＝sin ⎣⎢⎡⎦⎥⎤π2－⎝ ⎛⎭⎪⎫π4＋α＝cos ⎝ ⎛⎭⎪⎫π4＋α， ∴sin ⎝ ⎛⎭⎪⎫π4＋αsin ⎝ ⎛⎭⎪⎫π4－α＝sin ⎝ ⎛⎭⎪⎫π4＋αcos ⎝ ⎛⎭⎪⎫π4＋α＝12sin ⎝ ⎛⎭⎪⎫π2＋2α＝12cos2α＝12(1－2sin 2α)＝12⎣⎢⎡⎦⎥⎤1－2×⎝ ⎛⎭⎪⎫122＝14. [典例2] 若tan α＝13，tan(α＋β)＝12，则tan β＝________. 答案 17解析 因为tan α＝13，tan(α＋β)＝12， 所以tan β＝tan[(α＋β)－α]＝α＋β－tan α1＋α＋βα＝12－131＋12×13＝17. 方法指导 三角变换的关键是找到条件和结论中的角和式子结构之间的联系.变换中可以通过适当地拆角、凑角或对式子整体变形达到目的.。