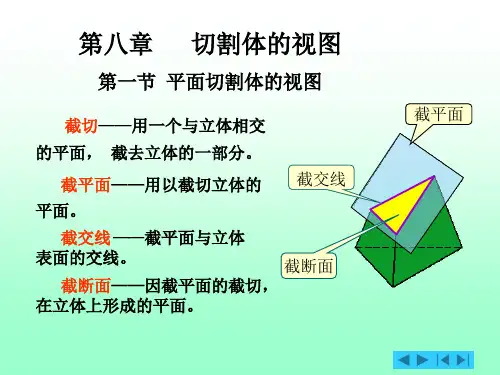
平面立体的切割
- 格式:pptx
- 大小:1.52 MB
- 文档页数:59

正方体的平面切割和截面特征正方体是一种六个面都相等且每个面都是直角四边形的立体图形。
平面切割是指将正方体沿着平面进行切割,从而得到不同的截面。
每个截面都有其特征和属性。
本文将探讨正方体平面切割和截面的特征。
首先,我们来了解一下正方体的基本属性。
正方体的六个面都是正方形,相邻面之间的边长相等。
通常,我们用字母a来表示正方体的边长。
此外,正方体的体积可以通过边长的三次方来计算,即V = a³;表面积可以通过边长的平方乘以六来计算,即S = 6a²。
接下来,我们讨论正方体的平面切割。
平面切割正方体时,切割面可以与正方体的面平行,也可以与正方体的面垂直。
对于平行切割,我们可以得到与正方体底面相似的平行四边形。
这些平行四边形的边长和对应边的长度比例与正方体底面相同。
当切割面与正方体的面垂直时,我们将得到线段、正方形、三角形或其他多边形的截面形状。
在平行切割的情况下,截面的特征与正方体的底面相似。
例如,如果我们将正方体平行地切割成一系列平行四边形,这些四边形的形状和相似性将与底面相同。
然而,它们的大小可能会有所不同,但比例关系将保持不变。
当切割面与正方体的面垂直时,截面的形状将根据切割的位置和角度而有所不同。
根据切割的位置,截面可以是线段、正方形、长方形、三角形或其他多边形。
在这些截面中,正方形和长方形出现的频率最高,因为它们是与正方体面相关联的形状。
此外,截面的边长可能与正方体的边长有关,但不一定相等。
当切割面与正方体的对角线平行时,我们将得到等腰直角三角形的截面。
这是因为对角线与正方体的边相切,并且正方体的边是直角的。
所以,切割面与对角线所包围出的截面将是等腰直角三角形。
在切割正方体时,我们还可以观察到一些有趣的截面特征。
例如,当切割面与相对的两条棱平行时,我们将得到矩形形状的截面。
这是因为切割面与这两条棱所包围出的空间将是一个矩形。
总结一下,正方体的平面切割和截面特征是多样化的。
通过平行或垂直切割,我们可以得到与正方体底面相似的平行四边形,以及线段、正方形、长方形、三角形或其他多边形的截面形状。



技术与应用A PPLICATION151OCCUPATION2014 10摘 要:所有复杂的零件都可以看成由一些基本体通过切割和叠加而成的组合体,切割相对于叠加对学生来说更加难以掌握。
笔者结合技工学校学生的特点,总结平面立体被切割的作图方法和步骤。
关键词:截交线 点的投影 作图方法平面立体被切割截交线的绘制方法文/周佳园 高 吉一、用单一平面切割平面立体以正六棱柱为例,讲解截交线的形成。
一是用之前所学习的基本体三视图的形成,让学生分析基本体的三视图,主要着重分析棱线的投影。
二是从截平面具有积聚性的视图入手,分析截平面截断了几条棱线,截交线就是几边形。
这里的棱线不仅包括侧棱线,还包括底面和顶面的底棱线和顶棱线,如图1所示。
此截平面为正垂面,在主视图上投影具有积聚性,从主视图入手解题,根据第一步的分析,截平面截断了三条侧棱线,两条顶棱线。
在主视图上标注出这五个点,如图1所示。
图1 图2三是这五个点在棱线上处于特殊位置,按照点的投影关系求出这五个点在俯视图和左视图上的投影,这一步让学生在黑板上完成,如图2所示。
四是把这五个点的同面投影连成线,擦去没用的线条,看不见的轮廓线改成虚线,如图3所示。
五是做完这道题目,教师变换截平面的位置,让学生自己按照刚才的方法,独立完成题目,然后教师再进行讲解,以达到巩固学习的目的。
图3 图4二、用组合平面切割平面立体以正四棱锥为例,讲解组合截交线的画法。
一是分析正四棱锥的三视图,在解棱锥被切割的问题时,建议把锥顶S 以及底面顶点A 、B 、C 、D 标记出来,这样求截交线的顶点在哪条棱线上、哪个棱面上,学生就一目了然了。
二是根据图4所示的截平面的位置,用两个组合平面切割正四棱锥时,两个平面在相交位置处会产生一条绞线,在做题时教师要一个截平面一个截平面地分析。
此时截交线的顶点不仅仅是位于棱线上,也会位于棱面上,教师要分析截平面切断几条棱线,两个平面的交线的顶点位于哪个侧棱面上,按照第一步的分析,根据SABCD 这样点的标记,可以分析出此位置有几条侧棱线。

探索立体几何中的平面切割数学教案目标:通过本节课的学习,学生能够掌握立体几何中的平面切割的概念、性质和应用,并能运用所学知识解决相关问题。
一、导入(5分钟)在黑板上画出一个简单的立体图形,让学生观察并描述该图形的特点和形状。
引导学生思考:如何将立体图形切割成平面图形?二、概念讲解与示例分析(15分钟)1. 定义平面切割:平面切割是指将立体图形切割成平面图形的过程。
2. 讲解平面切割的原理:平面切割可以通过在立体图形内部引入一个平面来实现。
3. 分析平面切割的常见形式:a. 平行切割:切割平面与立体图形平行。
b. 垂直切割:切割平面与立体图形垂直。
c. 斜切割:切割平面与立体图形既不平行也不垂直。
4. 给出具体示例,让学生通过切割平面得出平面图形的特点和性质。
三、性质总结与练习(20分钟)1. 性质总结:a. 平面切割后得到的平面图形的边界是原立体图形的一个截面。
b. 平切立体图形得到的平面图形与原图形相似。
c. 垂切立体图形得到的平面图形是原图形的一个截面。
d. 斜切立体图形得到的平面图形既不是原图形的截面,也不与原图形相似。
2. 练习:根据不同的平面切割形式,完成相关题目,巩固所学知识。
四、应用拓展(20分钟)1. 应用讨论:通过实际例子,引导学生思考在生活中使用平面切割的场景,并讨论其作用与意义。
2. 实例分析:给出一系列实际问题,让学生运用所学知识解决,包括计算切割平面的位置与角度,以及推断切割后平面图形的特点。
五、归纳总结(10分钟)总结平面切割的概念、原理、常见形式、性质和应用,并强调其在几何学和生活中的重要性。
六、师生互动(5分钟)与学生互动,检查学生对平面切割的理解程度,并解答学生的问题。
七、作业布置(5分钟)布置相关作业,要求学生进一步巩固和应用所学知识,包括练习题和实际问题。
八、板书设计(5分钟)根据学习内容,整理并梳理板书,突出重点和关键词。
九、课堂小结(5分钟)对本节课的学习内容进行小结,并鼓励学生继续深入思考和探索立体几何中的平面切割。

立体几何切割问题立体几何切割问题是几何学中的一类基本问题,它主要解决的是如何将某个物体以特定的方式分割成若干个部分。
在实际生产和工程设计中,常常需要进行对物体的切割以获得所需的形状。
因此,了解切割问题的解决方法具有重要的理论和实践意义。
立体几何切割问题的解决方法可以通过分割对象的不同特性进行分类。
一种方法是通过描绘物体的截面,从而得到物体的切割方式。
另一种方法是通过分割物体的表面,并找到该表面的交点,进而获得物体的容积信息。
以下是两种方法的详细解释。
一、基于截面的立体几何切割问题将物体以某个截面进行切割,并将其截面像平面上的平面图形一样进行处理是一种基本的方法。
这种方法的优势在于它可以更好地说明切割后的对象的几何形状。
截面也可以通过不同的角度进行描述,从而得到不同的结果。
例如,在平凡的情况下,一根棒子被真正地切断,其截面会是一个圆。
这个圆可以有不同的大小和角度,具体取决于切割的方向。
如果切割在不同的方向上,切割后的棒子也会有不同的直径和长度。
另一个例子是,一个正方体可以沿着不同的平面进行切割,从而得到不同的长度、宽度和高度。
在这种情况下,计算和说明截面的方向和形状是非常重要的。
通常,截面的描绘是通过使用几何图形、表格或公式进行。
这些描绘提供了对切割对象几何特征的详细描述,从而有助于理解其形状和结构。
二、基于表面交点的立体几何切割问题另一种常见的方法是基于物体表面上的交点。
在这种情况下,所考虑的问题是如何将一个物体分割,并在分割过程中识别其不同部分所占的容积。
这种方法通常用于确定物体大致的形状和大小,以及找到一些特殊的属性。
例如,在制作一个汽车座椅时,需要重点关注座椅底部与座垫之间的角度和弯曲。
如何确保它们完全契合,会影响座位的舒适度和安全性。
为了解决这些问题,需要首先对座椅进行切割,获得各部分的容积和尺寸信息。
对于这类问题,解决方案通常是通过将物体表面分成多个小区域,然后将它们的体积相加来获取该物体的总体积。

空间立体几何切割空间立体几何是研究三维物体的形状、大小和位置关系的数学分支。
在实际应用中,我们经常需要切割立体物体来获得所需的形状。
本文将介绍几种常见的空间立体几何切割方法。
一、平面切割平面切割是最基本和常见的几何切割方法之一。
它指的是通过平面将立体物体分割成两个或多个截面。
平面切割可以通过切割平面的不同位置和角度来得到不同的形状。
举例来说,我们可以通过一个平行于底面的平面来切割一个长方体,得到两个等面积的长方体。
这种切割方法可以被广泛应用于建筑设计、工程制图和数学研究等领域。
二、棱切割棱切割是指通过切割立体物体的棱来获得所需的形状。
一般情况下,我们可以通过连接棱的顶点来形成一个三角形或多边形,从而实现切割。
例如,在一个正方体上切割一条棱,得到两个等高的三棱柱。
棱切割在制作模型、造型设计和物理实验等领域具有广泛的应用。
三、面切割面切割是通过切割立体物体的一个或多个面来实现的。
常见的面切割方法有剪切和分割。
剪切是指通过沿着一条直线进行切割,比如通过剪刀将一个纸板剪成两半。
分割是指通过在一个面上绘制一条线,然后将该面沿着这条线切割,从而得到两个或多个切割后的面。
面切割在工程制图、艺术设计和数学研究等领域具有广泛的应用。
四、体切割体切割是通过切割立体物体的体积来实现的。
这种切割方法在某些情况下比其他方法更为复杂,需要使用特殊的切割工具。
例如,在木工制作中,使用电锯来切割木材。
体切割应用于雕刻、建模和制造等领域。
综上所述,空间立体几何切割是通过切割立体物体的不同部分来获得所需形状的方法。
常见的切割方法包括平面切割、棱切割、面切割和体切割。
这些切割方法在建筑设计、工程制图、艺术设计等领域有着广泛的应用。
通过合理选择切割方法,我们可以创造出各种复杂立体物体,并满足特定的设计需求。
希望本文能够帮助读者更好地理解空间立体几何切割的方法和应用,并在实际操作中得到运用。
通过深入研究和实践,我们可以不断拓展几何学的应用领域,为各个领域的发展做出贡献。


初中数学什么是切割
在数学中,切割是指将一个图形或物体分割成若干个部分的过程。
切割可以是平面的,也可以是立体的,常见的切割方式有直线切割和曲线切割。
下面我将详细介绍切割的概念、方法和应用:
1. 直线切割:
直线切割是指通过直线将一个图形或物体分割成若干个部分。
直线切割可以是平行切割和垂直切割两种形式。
-平行切割:通过平行线将图形或物体分割成平行的多个部分。
平行切割可以用于分割长方形、正方形等图形。
-垂直切割:通过垂直线将图形或物体分割成垂直的多个部分。
垂直切割可以用于分割三角形、梯形等图形。
2. 曲线切割:
曲线切割是指通过曲线将一个图形或物体分割成若干个部分。
曲线切割可以是任意曲线,如圆弧、抛物线等。
曲线切割常见的应用场景包括分割圆形、椭圆形等图形。
3. 切割的方法:
切割可以通过直线和曲线的组合来实现。
切割的方法可以根据具体的图形和要求来选择,常用的方法包括划线、切割工具等。
4. 切割的应用:
切割在几何学和图形处理中有广泛的应用,常见的应用包括:
-分割图形:切割可以将一个图形分割成若干个部分,便于研究和分析图形的性质和特征。
-制作模型:切割可以用于制作各种模型,如纸艺、拼图等,通过切割可以将平面图形转化为立体模型。
-制作拼图:切割可以用于制作各种拼图游戏,通过切割将图形分割成若干个小块,让人们通过拼接还原原始图形。
以上是关于切割的概念、方法和应用的介绍。
切割是数学中的重要概念,它可以帮助我们更好地理解和应用图形的分割和处理技术。
希望以上内容能够满足你对切割的了解。
切割法设计基础知识点切割法是一种常用的设计方法,可以应用于各种领域,包括工业设计、建筑设计、服装设计等。
在设计过程中,我们需要掌握一些基础的知识点,以确保设计的准确性和效果。
一、什么是切割法切割法是一种通过将设计对象或材料分割成不同的部分,然后再重新组合,以达到设计目的的方法。
这种方法可以帮助我们更好地理解对象的构造和形态,并在设计中进行有目的性的改动。
二、切割法的分类1. 平面切割法平面切割法是将设计对象或材料按照平面的方式进行切割,然后再重新组合的方法。
通过这种方法,我们可以改变对象的形状、比例和布局。
平面切割法常用于平面设计、海报设计等领域。
2. 立体切割法立体切割法是将立体的设计对象或材料按照不同的角度或方向进行切割,然后重新组合的方法。
通过这种方法,我们可以改变对象的整体结构、体积和立体感。
立体切割法常用于产品设计、建筑设计等领域。
三、切割法的应用场景1. 图形设计切割法在图形设计中应用广泛。
例如,在海报设计中,我们可以将图片和文字进行切割,然后重新组合,以达到突出重点、吸引眼球的效果。
2. 产品设计切割法在产品设计中也有很多应用。
例如,在家具设计中,可以利用切割法将不同形状的部件进行组合,形成独特的家具造型。
在汽车设计中,可以利用切割法将车身进行切割,形成流线型的外观。
3. 建筑设计切割法在建筑设计中常用于创造独特的建筑形态和空间感。
例如,在建筑立面设计中,可以利用切割法将立面进行切割,形成凹凸有致的立体效果。
在室内设计中,可以利用切割法将空间进行划分和组合,形成不同功能区域。
四、切割法的设计原则1. 形态统一原则在切割法的设计中,要保持整体形态的统一,避免切割所产生的部分片段脱离整体的感觉。
切割的部分应当与整体形状相互呼应,形成一种和谐的整体效果。
2. 功能实用原则切割不仅要考虑设计效果,还要考虑实际使用功能。
在设计过程中,要合理切割,确保切割后的部分仍然具备原本的功能,并且能够满足用户的需求。
立体形状切割问题问题概述立体形状切割问题是指在给定一个立体形状的情况下,将其切割成多个平面形状的过程。
这个问题在许多实际应用中都是非常重要的,比如在制造业中的材料切割、建筑业中的构件制作等。
问题分类立体形状切割问题可以分为两种基本类型:二维图形切割和三维物体切割。
二维图形切割二维图形切割是指在给定一个平面形状的情况下,将其切割成多个平面形状的过程。
这个问题通常将平面形状表示为一个轮廓线,通过切割线将其切割成多个封闭的子图形。
三维物体切割三维物体切割是指在给定一个立体形状的情况下,将其切割成多个平面形状的过程。
这个问题通常将立体形状表示为一组三维坐标点的集合,通过切割平面将其切割成多个子物体。
解决方法解决立体形状切割问题的方法有很多,下面介绍几种常见的方法。
欧几里得凸壳算法欧几里得凸壳算法是一种常用的解决二维图形切割问题的方法。
该算法先通过一组点计算出其凸壳,然后通过凸壳上的一段线将原始图形切割成两个子图形。
这个过程可以递归进行,直到无法再切割为止。
体积切割算法体积切割算法是一种常用的解决三维物体切割问题的方法。
该算法通过定义切割平面的位置和方向来实现物体的切割。
切割平面可以通过计算物体外围点的凸壳得到,或者通过用户输入进行定义。
切割过程可以使用类似于欧几里得凸壳算法的递归方式。
虚拟切割算法虚拟切割算法是一种常用的解决立体形状切割问题的方法。
该算法通过在立体形状内部虚拟划定一个切割平面,然后将其与实际切割平面进行比较,得到切割结果。
虚拟切割算法常用于需要考虑物体内部结构的问题,如骨骼切割、器官切割等。
应用领域立体形状切割问题广泛应用于各个领域,如制造业、建筑业、医疗等。
在制造业中,立体形状切割问题被广泛用于材料切割,可以帮助提高材料利用率,减少浪费。
在建筑业中,立体形状切割问题被用于制作构件。
通过合理切割立体形状的材料可以大幅度减少构件的成本,提高生产效率。
在医疗领域中,立体形状切割问题被用于医学影像处理。