第四节直线的投影投影的基本知识、特定和定理
- 格式:ppt
- 大小:1.94 MB
- 文档页数:66

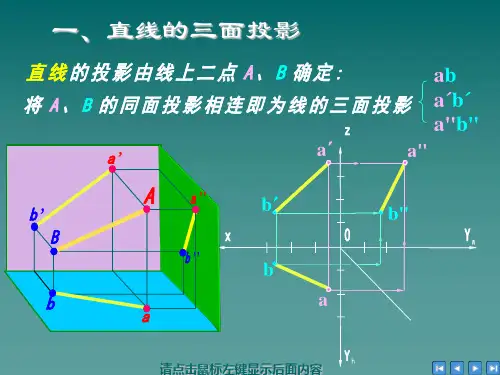


第四节直线的投影空间两点确定一条空间直线段,空间直线的投影一般也是直线。
直线段投影的实质,就 是线段两个端点的同面投影的连线;所以学习直线的投影,必须于点的投影联系起来。
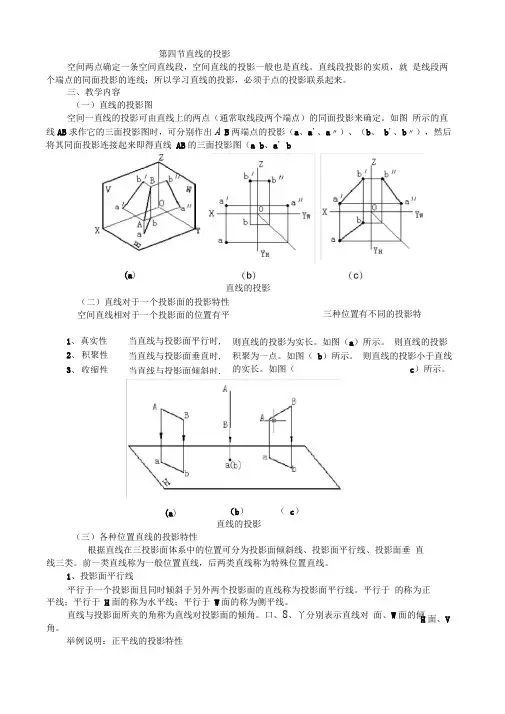
三、教学内容(一)直线的投影图空间一直线的投影可由直线上的两点(通常取线段两个端点)的同面投影来确定。
如图 所示的直线AB 求作它的三面投影图时,可分别作出A B 两端点的投影(a 、a '、a 〃)、(b 、 b '、b 〃),然后将其同面投影连接起来即得直线 AB 的三面投影图(a b 、a ' b(a )直线的投影(二)直线对于一个投影面的投影特性 空间直线相对于一个投影面的位置有平三种位置有不同的投影特1、 真实性2、 积聚性3、 收缩性当直线与投影面平行时, 当直线与投影面垂直时, 当直线与投影面倾斜时, 则直线的投影为实长。
如图(a )所示。
则直线的投影积聚为一点。
如图( b )所示。
则直线的投影小于直线的实长。
如图(c )所示。
(b )( c )直线的投影(三)各种位置直线的投影特性根据直线在三投影面体系中的位置可分为投影面倾斜线、投影面平行线、投影面垂 直线三类。
前一类直线称为一般位置直线,后两类直线称为特殊位置直线。
1、投影面平行线 平行于一个投影面且同时倾斜于另外两个投影面的直线称为投影面平行线。
平行于 的称为正平线;平行于 H 面的称为水平线;平行于 W 面的称为侧平线。
直线与投影面所夹的角称为直线对投影面的倾角。
口、8、丫分别表示直线对 面、W 面的倾角。
举例说明:正平线的投影特性H 面、V Y(a )V作正垂线AB强调:(1)斜线反映实长;(2)直线的倾角a 、Y 。
总结投影面平行线的投影特性:两平一斜。
要求学生必须掌握表中的图例。
对于投影面平行线的辨认:当直线的投影有两个平行于投影轴, 第三投影与投影轴倾斜时,则该直线一定是投影面平行线,且一定平 行于其投影为倾斜线的那个投影面。

直线投影的知识点总结1. 投影的概念投影是指将三维空间中的物体通过某种方法映射到二维平面上,以展示其形状和大小的过程。
在工程制图中,投影是一种重要的表达方式,可以帮助人们更直观地理解和表达物体的结构和形状。
2. 投影的分类在工程制图中,投影可以分为直线投影和透视投影两种。
直线投影是指在投影过程中光线是平行的,而透视投影则是考虑了远近距离的差异,因此在投影过程中光线是呈放射状的。
3. 投影的原理直线投影的原理基于光线在空间中的传播规律,根据几何关系将三维物体在平面上做投影。
当物体的每一个点都按一定的比例在平面上映射时,就得到了这个物体的投影。
4. 投影的图法表示在工程制图中,人们通常使用图法来表示物体的投影。
常用的有正投影、等轴测投影和三视图投影。
正投影是指投影方向与平面垂直,等轴测投影则是将物体在不同方向上进行投影,以展现其三维的效果。
而三视图投影则是将物体从不同方向进行投影,得到其正视图、侧视图和俯视图。
5. 投影的方法直线投影有多种方法,包括平行投影、斜投影和透视投影。
平行投影是最常见的一种方法,即在投影过程中光线是平行的。
而斜投影则是在投影过程中光线是不平行的,透视投影则是考虑了物体的远近距离。
6. 投影的规律在直线投影过程中,有一些规律是需要遵循的。
比如投影点要按比例映射、同类图形投影相似等。
因此,在进行投影时需要谨记这些规律。
7. 投影的应用直线投影在工程领域有着广泛的应用,比如在建筑设计、机械制图、电路设计等领域都需要使用到投影技术。
只有通过投影,人们才能更清晰地了解和表达物体的结构和形状。
8. 投影的发展随着科技的不断进步,投影技术也在不断发展。
比如在虚拟现实、增强现实等领域,投影技术也有所应用。
未来,投影技术将会更加多样化和智能化,为人们的生活和工作带来更多便利。
总之,直线投影是工程图学中一种重要的技术手段,它通过将三维物体在平面上做投影,展示其真实大小和形状。
了解直线投影的知识点对于从事相关工程行业的人员来说是十分必要的。





直线与平面投影知识点总结在几何学中,直线与平面的投影是一个重要的概念。
它们常常出现在三维空间的几何关系中,同时也在工程学、物理学等领域中有着广泛的应用。
在本文中,我们将主要介绍直线与平面的投影的基本概念、性质和应用。
一、直线的投影:1. 直线的投影定义:在三维空间中,如果一个直线与一个平面相交,那么这条直线在这个平面上的投影就是直线在该平面上的影子。
投影是一个向量,它的方向是垂直于平面,并且与直线平行。
投影的长度等于直线在该方向上的投影长度。
2. 直线的投影性质:(1)如果平行于平面的直线在平面上的投影为一线段,则该线段的中垂线必然在平面上。
(2)如果垂直于平面的直线在平面上的投影是一个点,则该点在平面上。
(3)直线在平面上的投影长度等于直线在法向量方向上的投影长度。
3. 直线的投影应用:(1)在工程制图中,需要将三维物体的投影绘制在二维平面上,这就涉及到了直线的投影。
(2)在几何学中,研究直线在平面上的投影可以帮助我们理解平行与垂直关系。
二、平面的投影:1. 平面的投影定义:在三维空间中,如果一个平面与一个平面相交,那么这个平面在另一个平面上的投影就是该平面在另一个平面上的影子。
平面的投影通常是一个多边形。
2. 平面的投影性质:(1)如果平行于平面的平面在另一个平面上的投影是一个多边形,则该多边形的边界一定是一个多边形的投影。
(2)如果垂直于平面的平面在另一个平面上的投影是一个点,则该点在另一个平面上。
3. 平面的投影应用:(1)在工程制图中,需要将三维物体的投影绘制在二维平面上,这就涉及到了平面的投影。
(2)在建筑设计中,考虑到平面的投影会对建筑物的外观和结构有着重要的影响。
三、直线与平面的投影:1. 直线与平面的投影定义:在三维空间中,如果一条直线与一个平面相交,那么这条直线在这个平面上的投影就是直线在该平面上的影子。
同样地,如果一个平面与一个平面相交,那么这个平面在另一个平面上的投影就是该平面在另一个平面上的影子。