根轨迹实验方案

实验三 根轨迹分析一、实验目的：1.熟悉零、极点对根轨迹的影响2.组合典型环节按照题目完成相应曲线二、实验内容鱼鹰型倾斜旋翼飞机V-22既是一种普通飞机，又是一种直升机。

当飞机起飞和着陆时，其发动机位置可以使V-22像直升机那样垂直起降，而在起飞后，它又可以将发动机旋转90度，切换到水平位置，像普通飞机一样飞行。

在直升机模式下，飞机的高度控制系统如图所示。

要求：（1） 概略绘出当控制器增益K1变化时的系统根轨迹图，确定使系统稳定的K1值范围； （2） 当取K1=280时，求系统对单位阶跃输入r(t)=l(t)的实际输出h(t)，并确定系统的超调量和调节时间（Δ=2%）；（3） 当K1=280，r(t)=0时，求系统对单位阶跃扰动N （s ）=1/s 的输出h n (t)； （4） 若在R （s ）和第一个比较点之间增加一个前置滤波器 G p (s)=5.05.15.02++s sMatlab 指令如下 fenzi=[1 1.5 0.5]; fenmu=[1 0];G1=tf(fenzi,fenmu) fenzi=[1];fenmu=conv(conv([20 1],[10 1]),[0.5 1]); G2=tf(fenzi,fenmu) sys1=series(G1,G2) rlocus(sys1)sys2=feedback(280*sys1,1) step(sys2)sys3=feedback(G2,280*G1) step(sys3)G3=tf([0.5],[1 1.5 0.5]) sys4=series(G3,sys2) step(sys4)（1）（3）(2)（4）三、结果分析1.根在左半平面，系统稳定；根在虚轴上临界稳定；根在右半平面系统不稳定。

2.当k>1时，特征方程为一对共轭复根，系统为欠阻尼系统，单位阶跃响应为阻尼振荡过程，振荡幅度或超调量随k值的增加而增大，但调整时间不会有显著变化。

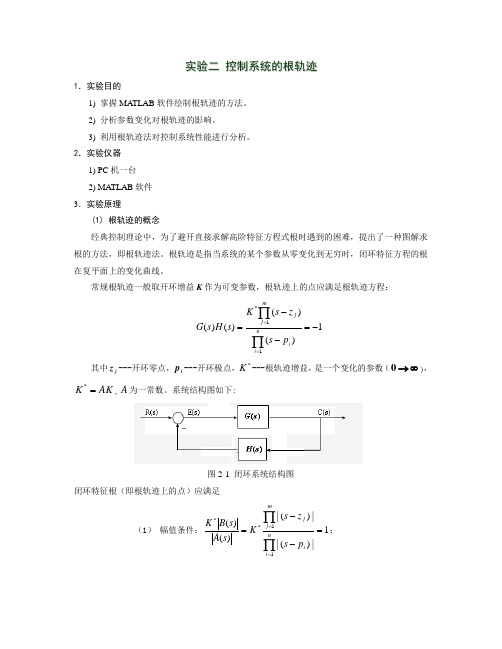
实验二 控制系统的根轨迹1．实验目的1) 掌握MA TLAB 软件绘制根轨迹的方法。

2) 分析参数变化对根轨迹的影响。

3) 利用根轨迹法对控制系统性能进行分析。

2．实验仪器1) PC 机一台 2) MATLAB 软件 3．实验原理(1) 根轨迹的概念经典控制理论中，为了避开直接求解高阶特征方程式根时遇到的困难，提出了一种图解求根的方法，即根轨迹法。

根轨迹是指当系统的某个参数从零变化到无穷时，闭环特征方程的根在复平面上的变化曲线。

常规根轨迹一般取开环增益K 作为可变参数，根轨迹上的点应满足根轨迹方程：1)()()()(11*-=--=∏∏==ni imj jp s zs Ks H s G其中j z ---开环零点，i p ---开环极点，*K ---根轨迹增益，是一个变化的参数（∞→0），AK K =*,A 为一常数。

系统结构图如下:图2-1 闭环系统结构图闭环特征根（即根轨迹上的点）应满足（1） 幅值条件：1|)(||)(|)()(11**=--=∏∏==n i imj jp s zs K s A s B K ；（2） 相角条件：π)12()()(11+=-∠--∠∑∑==k p s zs ni i mj j。

（2）用MATLAB 软件绘制根轨迹MATLAB7.0提供的工具箱给出了一系列关于根轨迹的函数，如表2-1所示。

使用这些函数能够很方便地绘制出系统的常规根轨迹和参数根轨迹，还能基于根轨迹对系统性能进行分析。

表2-1 根轨迹函数① pzmap调用格式：pzmap(sys); [p,z]=pzmap(sys) ② rlocfind调用格式：[k,poles]=rlocfind(sys); [k,poles]=rlocfind(sys,p) ③ rlocus调用格式：rlocus(sys); rlocus(sys,k); [r,k]=rlocus(sys); r=rlocus(sys,k) ④ rltool调用格式：rltool(plant); rltool(plant,comp) ⑤ sgrid调用格式：sgrid; sgrid(z,wn) ⑥ zgrid调用格式：zgrid; zgrid(z,wn) 4．实验内容与步骤系统的开环传递函数：)2)(1()()(*++=s s s K s H s G绘制系统的根轨迹图。

第1篇一、实验目的1. 理解并掌握根轨迹的概念及其在控制系统中的应用。

2. 学习使用MATLAB软件绘制系统的根轨迹。

3. 通过根轨迹分析，了解系统参数变化对系统性能的影响。

4. 熟悉根轨迹法在控制系统设计中的应用，如稳定性分析、参数整定等。

二、实验原理根轨迹是指系统的某一参数（如开环增益K）从零变到无穷大时，系统闭环特征根在复平面上变化轨迹。

通过根轨迹，可以直观地分析系统的稳定性、过渡过程和稳态误差等性能指标。

三、实验设备1. 计算机：安装MATLAB软件。

2. 控制系统实验箱。

四、实验步骤1. 建立系统模型根据实验要求，建立系统的传递函数模型。

例如，对于一个二阶系统，其传递函数可以表示为：$$G(s) = \frac{K}{(s+a)(s+b)}$$其中，a和b为系统的时间常数，K为开环增益。

2. 绘制根轨迹使用MATLAB软件中的rlocus函数绘制系统的根轨迹。

rlocus函数的调用格式如下：```matlabrlocus(num, den)```其中，num和den分别为系统的分子和分母多项式系数。

3. 分析根轨迹（1）观察根轨迹的起始点和终止点，判断系统的稳定性。

（2）分析根轨迹的形状，了解系统参数变化对系统性能的影响。

（3）确定系统临界增益和临界阻尼比。

4. 验证实验结果通过改变系统参数，观察根轨迹的变化，验证实验结果。

五、实验结果与分析1. 绘制根轨迹使用MATLAB软件绘制了给定二阶系统的根轨迹，如图1所示。

从图中可以看出，随着开环增益K的增加，系统闭环极点逐渐向左移动，系统稳定性提高。

2. 分析根轨迹（1）起始点和终止点：根轨迹的起始点为系统的开环极点，终止点为系统的开环零点。

（2）根轨迹形状：根轨迹呈对称形状，随着开环增益K的增加，根轨迹逐渐向左移动。

（3）临界增益和临界阻尼比：通过观察根轨迹，可以确定系统的临界增益和临界阻尼比。

根轨迹法的课程设计一、课程目标知识目标：1. 让学生掌握根轨迹法的概念、原理和应用范围；2. 使学生理解根轨迹法在系统稳定性分析中的重要性；3. 引导学生运用根轨迹法分析控制系统性能，并能绘制根轨迹图；4. 帮助学生掌握根据根轨迹图判断系统稳定性的方法。

技能目标：1. 培养学生运用根轨迹法分析实际控制系统的能力；2. 提高学生绘制根轨迹图、判断系统稳定性的技巧；3. 培养学生运用数学软件（如MATLAB）辅助根轨迹分析的能力。

情感态度价值观目标：1. 培养学生对自动控制理论的学习兴趣，激发学生探索科学问题的热情；2. 培养学生团队合作精神，学会倾听他人意见，尊重他人成果；3. 增强学生面对复杂问题时的分析、解决问题的信心，培养勇于克服困难的品质。

课程性质：本课程为自动控制理论课程的一部分，旨在帮助学生掌握根轨迹法这一重要的稳定性分析方法。

学生特点：学生已具备一定的控制系统基础知识，具有一定的数学基础和分析能力。

教学要求：结合学生特点和课程性质，将课程目标分解为具体的学习成果，通过理论讲解、案例分析、上机实践等教学手段，使学生在理解根轨迹法的基础上，能够将其应用于实际控制系统的分析。

同时，注重培养学生的实际操作能力和团队合作精神，提高学生的综合素质。

二、教学内容1. 引入根轨迹法的基本概念，阐述其在控制系统稳定性分析中的作用；2. 讲解根轨迹法的原理，包括根轨迹的定义、绘制方法及其与系统稳定性的关系；3. 介绍根轨迹图的绘制步骤，结合教材实例进行分析；- 确定系统的开环传递函数；- 求解开环极点、零点；- 应用根轨迹规则，绘制根轨迹图；- 分析根轨迹图与系统稳定性的关系。

4. 分析不同控制系统参数变化对根轨迹的影响，探讨参数变化对系统稳定性的影响；5. 介绍利用根轨迹法进行控制系统性能优化，包括调整系统参数以改善稳定性；6. 结合实际案例，运用根轨迹法进行控制系统分析，提高学生解决实际问题的能力；7. 使用数学软件（如MATLAB）辅助根轨迹分析，让学生掌握相关软件操作技巧。

根轨迹实验报告根轨迹实验报告引言：根轨迹是控制系统理论中的一个重要概念，它描述了系统在参数变化下的稳定性和响应特性。

本实验旨在通过实际操作和数据分析，深入理解根轨迹的原理和应用。

通过对比不同系统的根轨迹，可以更好地理解系统的稳定性和控制性能。

一、实验目的本实验的目的是通过实际操作和数据分析，加深对根轨迹的理解，掌握根轨迹的绘制方法和分析技巧。

同时，通过对比不同系统的根轨迹，分析系统参数对根轨迹的影响，进一步认识系统的稳定性和控制性能。

二、实验装置与方法实验所需的装置包括控制系统实验台、计算机和相应的控制软件。

实验过程中，首先将系统接入实验台，通过控制软件设置系统参数，然后进行数据采集和分析。

根据实验要求，可以改变系统参数、增加干扰等，观察根轨迹的变化。

三、实验结果与分析在实验过程中，我们分别绘制了不同系统的根轨迹，并进行了数据分析。

通过观察根轨迹的形状和位置，我们可以判断系统的稳定性和响应特性。

以一个简单的一阶系统为例，我们改变了系统的比例增益和时间常数，绘制了对应的根轨迹。

通过观察根轨迹的位置和形状，我们可以发现以下规律：当比例增益增大时，根轨迹向左移动，系统的稳定性增强；当时间常数增大时，根轨迹变得更加平缓，系统的响应速度变慢。

在另一个二阶系统的实验中，我们改变了系统的阻尼比和自然频率，绘制了对应的根轨迹。

通过观察根轨迹的形状和分布，我们可以得出以下结论：当阻尼比增大时，根轨迹变得更加收敛，系统的稳定性提高；当自然频率增大时，根轨迹变得更加散布，系统的响应速度增加。

通过对比不同系统的根轨迹，我们可以进一步分析系统的稳定性和控制性能。

例如，当两个系统的根轨迹重合或者相似，可以认为它们具有相似的稳定性和响应特性；而当根轨迹相交或者离散较大时，可能存在系统不稳定或者不良的控制性能。

四、实验总结通过本次实验，我们深入了解了根轨迹的原理和应用。

通过实际操作和数据分析，我们掌握了根轨迹的绘制方法和分析技巧。

线性系统的根轨迹法实验报告实验二线性系统的根轨迹法一,实验目的1，掌握matlab绘制根轨迹的方法。

2，观察k值变化对系统稳定性的影响。

3，掌握系统临界稳定情况下k值得求取。

4，了解增设零点对系统稳定的影响以及改善系统稳定性的方法。

二，实验原理根轨迹的概念:所谓根轨迹就是当开环系统某一参数从零变到无穷大时，闭环系统特征方程式的根在s平面上变化的轨迹。

根轨迹与系统性能:有了根轨迹就可以分析系统的各种性能了，稳定性的判定，当开环增益从零变到无穷大时，根轨迹不会越过虚轴进入s平面的右半平面，此时K的范围为系统稳定的范围，根轨迹与虚轴的交点处的K值，为系统的临界开环增益，开根轨迹进入s平面的右半平面时所对应的K值为系统不稳定的情况。

三，实验内容A、设单位负反馈系统的开环传递函数为G(s)=K/(s*(s+1)(s+5)) (1) 绘制系统的根轨迹，并将手工绘制结果与实验绘制结果比较; (2) 从实验结果上观察系统稳定的K 值范围;(3) 用simulink 环境观察系统临界稳定时的单位阶跃响应分析:绘制根轨迹的matlab文本为clfnum=1;den=conv([1 1 0],[1 5]); rlocus(num,den) %绘制系统根轨迹1,得到如图的根轨迹图:2,用鼠标点击根轨迹与虚轴处的交点可得到临界稳定的开环增益K=30,所以系统稳定的K值范围为0―30。

3，在simulink环境下按下图连接电路:取增益为30的时候在示波器下观察单位节约响应，输出波形为:由图可以看出单位阶跃响应的输出为等幅的震荡输出，所以此时系统为临界稳定状态。

当改变开环增益为50和20时观察示波器，得到输出波形分别为:由图可知当增益K为50时输出为不稳定的震荡输出，此时系统不稳定，当增益K为20时输出的波形震荡越来越缓慢，最后趋于稳定，所以此时的系统是稳定的。

B，设单位反馈控制系统的开环传递函数为G(S)=K(s+3)/s(s+1)(s+2)(1) 仿照上题绘制系统的根轨迹，并判断系统的稳定性; 参照第一题得到matlab命令文本为:clfnum=1;den=conv([1 1 0],[1 2]); rlocus(num,den) %绘制系统根轨迹得到如图的根轨迹图:1，由图可知根轨迹没有进入s平面右半平面，所以系统在K=0到K=?都是稳定的。

|实验四 用MATLAB 绘制根轨迹图 （The Root Locus Using MATLAB ）一、绘制系统的根轨迹在绘制根轨迹之前，先把系统的特征方程整理成标准根轨迹方程r num(s)1+G(s)H(s)=1+K =0den(s)⋅其中：rK为根轨迹增益；num(s)为系统开环传递函数的分子多项式；den(s)为系统开环传递函数的分母多项式。

绘制根轨迹的调用格式有以下三：rlocus(num,den) 开环增益k 的范围自动设定； rlocus(num,den,k) 开环增益k 的范围人工设定； [K,p]=rlocfind(G ) 确定所选定处的增益和对应的特征根。

例4.1 已知某系统的开环传递函数为s s s s K s r 424)(23+++⋅=G试绘制该系统的根轨迹。

解： 在Matlab 命令窗口键入 num=[1 4];den=[1 2 4 0]; rlocus(num,den)可得如图4-1的结果。

-5-4-3-2-11-10-8-6-4-20246810Real AxisI m a g i n a r y A x i sRoot Locus图4-1由于采用rlocus()函数绘制根轨迹时，不同的根轨迹分支之间只区分颜色而不区分线形，所以打印时是不容易分辨各个分支的，需要在运行Matlab 程序时注意观察曲线的颜色。

■例4-2 若要求例4-1中的r K 在1到10之间变化，绘制相应的根轨迹。

解 在MATLAB 命令窗口键入 num=[1 4];den=[1 2 4 0];k=[1:0.5:10]; rlocus(num,den,k)可得如图4-2.的结果。

-4.5-4-3.5-3-2.5-2-1.5-1-0.500.5Root LocusReal AxisI m a g i n a r y A x i s图4-2例4-3 设系统的开环传递函数为)22)(3(()(2+++=s s s K s s rs H G ）试绘制其闭环系统的根轨迹图并在图上找出几点的相关数据。

自动控制原理实验报告实验三 控制系统根轨迹实验即课后习题4-221．G ＊=)()1(2a s s K s ++, 当系统具有一个、两个或没有分离点时，作出系统跟轨迹。

解：由d 1+d 1+a d +1=11+d 得 2d 2+（3+a ）d+2a=0; 当△=a 2-10a+9>0，即a>9或a<1时有两个分离点。

当△=a 2-10a+9=0，即a=9或a=1时有一个分离点。

当△=a 2-10a+9<0，即1<a<9时没有分离点。

当a 分别取9、1、5、20。

代码如下，根轨迹如下图a1=9;a2=1;a3=5a4=20;G1=zpk([-1],[0 0 -a1],1)G2=zpk([-1],[0 0 -a2],1)G3=zpk([-1],[0 0 -a3],1)G4=zpk([-1],[0 0 -a4],1)subplot(141)rlocus(G1)title('a=9')subplot(142)rlocus(G2)title('a=1')subplot(143)rlocus(G3)title('a=5')subplot(144)rlocus(G4)title('a=20')从上图可以看出a=9时，有一个分离点，与计算出的分离点-3相符。

a=1时，有一个分离点，与计算出的分离点-1相符。

a=5时，没有分离点。

a=20时，有2个分离点，与计算出的分离点-8.9221、-2.5779相符。

2．G =)3)(1)(1(++-s s s K ，增加零点分别为:-2,-0.5,作出不同情况下的根轨迹。

解：代码和根轨迹如下：a1=2;a2=0.5;G1=zpk([],[1 -1 -3],1)G2=zpk([-a1],[1 -1 -3],1)G3=zpk([-a2],[1 -1 -3],1)subplot(141)rlocus(G1)title('原图')axis([-5 5 -6 6])subplot(142)rlocus(G2)title('增加-2零点')axis([-5 5 -6 6])subplot(143)rlocus(G3)title('增加-0.5零点')axis([-5 5 -6 6])通过根轨迹图可以清楚的发现增加负零点，根轨迹左移，零点与虚轴越近，作用越显著。

根轨迹法校正 课程设计一、课程目标知识目标：1. 学生能够理解根轨迹法的概念，掌握根轨迹的基本绘制方法。

2. 学生能够运用根轨迹法分析控制系统的稳定性，并识别系统的性能指标。

3. 学生能够掌握通过根轨迹法进行控制系统校正的基本原理和步骤。

技能目标：1. 学生能够独立绘制根轨迹图，并分析控制系统的稳定性。

2. 学生能够运用根轨迹法设计简单的控制系统校正方案，提高系统性能。

3. 学生能够通过实际案例，运用所学知识解决控制系统中的实际问题。

情感态度价值观目标：1. 培养学生对自动控制系统的兴趣，激发他们的探究欲望。

2. 培养学生严谨的科学态度，使他们认识到理论知识在实际工程中的重要性。

3. 培养学生的团队协作意识，使他们能够在小组合作中发挥自己的专长，共同解决问题。

课程性质：本课程为自动控制系统相关内容的深化学习，旨在帮助学生掌握根轨迹法校正的基本原理和方法，提高学生分析问题和解决问题的能力。

学生特点：学生已具备一定的自动控制理论知识，具有一定的数学基础和动手能力。

教学要求：结合学生特点，注重理论与实践相结合，通过案例分析和实际操作，使学生能够将所学知识应用于控制系统设计和分析中。

同时，注重培养学生的团队合作能力和创新意识。

在教学过程中，关注学生的学习进度，及时调整教学方法和节奏，确保课程目标的实现。

二、教学内容1. 根轨迹基本概念：根轨迹的定义、意义及其在控制系统中的应用。

- 教材章节：第三章第二节- 内容：根轨迹图的绘制方法、关键点和关键轨迹的特点。

2. 控制系统稳定性分析：利用根轨迹分析系统稳定性，判断系统性能。

- 教材章节：第三章第三节- 内容：稳定性的判定条件、稳定性分析步骤。

3. 根轨迹校正原理：介绍根轨迹法校正控制系统的基础知识。

- 教材章节：第三章第四节- 内容：校正的基本原理、常用校正方法及效果分析。

4. 校正方案设计：结合实际案例，设计控制系统校正方案。

- 教材章节：第三章第五节- 内容：校正方案的设计步骤、参数计算方法、系统性能优化。

《自动控制原理》实验报告题目：根轨迹的绘制及系统分析专业：电子信息工程班级：姓名：学号：实验二根轨迹的绘制及系统分析一、实验目的1．熟练掌握使用MATLAB软件绘制根轨迹图形的方法；2．进一步加深对根轨迹图的了解；3．利用所绘制根轨迹图形分析系统性能。

二、实验内容本实验中各系统均为负反馈控制系统，系统的开环传递函数形式为：11()()()()mi i njj K s z G s H s s p ==-=-∏∏（一）已知系统开环传递函数分别为如下形式：（1）()()(1)(2)KG s H s s s =++（2）(3)()()(1)(2)K s G s H s s s +=++（3）(3)()()(1)(2)K s G s H s s s -=++（4）()()(1)(2)(3)KG s H s s s s =+++（5）()()(1)(2)(3)KG s H s s s s =++-1、绘制各系统的根轨迹；2、根据根轨迹判断系统稳定性；如果系统是条件稳定的（有根轨迹分支穿越虚轴），试确定稳定条件（K 值取值范围）；（1）代码及截图 num=[1];den=conv([1 1],[1 2]); rlocus(num,den)-2.5-2-1.5-1-0.500.5-0.8-0.6-0.4-0.20.20.40.60.8Root LocusReal AxisI m a g i n a r y A x i s根轨迹全部落在左半S 平面上，该系统稳定。

（2）代码及截图 num=[1 3];den=conv([1 1],[1 2]); rlocus(num,den)Root LocusReal AxisI m a g i n a r y A x i s-9-8-7-6-5-4-3-2-101-1.5-1-0.50.511.5System: sys Gain: 5.83Pole: -4.51Damping: 1Overshoot (%): 0Frequency (rad/sec): 4.51System: sys Gain: 0.0129Pole: -1.03Damping: 1Overshoot (%): 0Frequency (rad/sec): 1.03System: sys Gain: 0.00236Pole: -2Damping: 1Overshoot (%): 0Frequency (rad/sec): 2根轨迹全部落在左半S 平面上，该系统稳定。